Скачать презентацию Понятие поверхности второго порядка Поверхность второго Скачать презентацию Понятие поверхности второго порядка Поверхность второго

Понятие поверхности второго порядка.ppt

  • Количество слайдов: 145

Понятие поверхности второго порядка Понятие поверхности второго порядка

Поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению Поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a 11 х2 + а 22 у2 + a 33 z 2+ 2 a 12 xy + 2 a 23 уz + 2 a 13 xz + 2 а 14 x + 2 а 24 у+2 а 34 z +а 44 = 0 (1) в котором по крайней мере один из коэффициентов a 11 , а 22 , a 33 , a 12 , a 23 , a 13 отличен от нуля. Уравнение (1) мы будем называть общим уравнением поверхности второго порядка. Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной декартовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравнение (1) и уравнение, полученное после преобразования координат, алгебраически эквивалентны.

Классификация поверхностей второго порядка Классификация центральных поверхностей. Пусть S — центральная поверхность второго порядка. Классификация поверхностей второго порядка Классификация центральных поверхностей. Пусть S — центральная поверхность второго порядка. Перенесем начало координат в центр этой поверхности, а затем произведем стандартное упрощение уравнения этой поверхности. В результате указанных операций уравнение поверхности примет вид a 11 х2 + а 22 у2 + a 33 z 2 + а 44 = 0 (2)

• Так как инвариант I 3 для центральной поверхности отличен от ноля и • Так как инвариант I 3 для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения (2) , равно a 11 • а 22 • a 33 , то коэффициенты a 11 , а 22, a 33 удовлетворяют условию: a 11 ≠ 0, а 22 ≠ 0, a 33≠ 0. • Возможны следующие случаи:

• Коэффициенты a 11 , а 22 , a 33 одного знака, а • Коэффициенты a 11 , а 22 , a 33 одного знака, а коэффициент а 44 отличен от нуля. В этом случае поверхность S называется эллипсоидом. • Если коэффициенты a 11 , а 22 , a 33 , а 44 одного знака, то левая часть (2) ни при каких значениях х, у, z не обращается в нуль, т. е. уравнению поверхности S не удовлетворяют координаты никакой точки. В этом случае поверхность S называется мнимым эллипсоидом.

Если знак коэффициентов a 11 , а 22 , a 33 противоположен знаку Если знак коэффициентов a 11 , а 22 , a 33 противоположен знаку коэффициента а 44, то поверхность S называется вещественным эллипсоидом. В дальнейшем термином «эллипсоид» мы будем называть лишь вещественный эллипсоид. Обычно уравнение эллипсоида записывают в канонической форме. Очевидно, числа: - а 44/ a 11, - а 44/ a 22, - а 44/ a 33 - положительны. Обозначим эти числа соответственно а 2, b 2, с2. После несложных преобразований уравнение эллипсоида (2) можно записать в следующей форме:

• (3) • Уравнение (3) называется каноническим уравнением эллипсоида. • Если эллипсоид задан • (3) • Уравнение (3) называется каноническим уравнением эллипсоида. • Если эллипсоид задан своим каноническим уравнением (3), то оси Ох, Оу и Оz. называются его главными осями.

2. Из четырех коэффициентов a 11 , а 22 , a 33 , 2. Из четырех коэффициентов a 11 , а 22 , a 33 , а 44 два одного знака, а два других— противоположного. В этом случае поверхность S называется однополостным гиперболоидом. Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности, a 11 > 0, а 22 > 0, a 33 < 0, а 44 < 0. Тогда числа - а 44/ a 11, - а 44/ a 22, а 44/ a 33 положительны. Обозначим эти числа соответственно а 2, b 2, с2. После несложных преобразований уравнение (2) однополостного гиперболоида можно записать в следующей форме:

(4) Уравнение (4) называется каноническим уравнением однополостного гиперболоида. Если однополостный гиперболоид задан своим (4) Уравнение (4) называется каноническим уравнением однополостного гиперболоида. Если однополостный гиперболоид задан своим каноническим уравнением (4), то оси Ох, Оу и Oz называются его главными осями.

3. Знак одного из первых трех коэффициентов a 11 , а 22 , 3. Знак одного из первых трех коэффициентов a 11 , а 22 , a 33 , а 44 противоположен знаку остальных коэффициентов. В этом случае поверхность S называется двуполостным гиперболоидом. Запишем уравнение двуполостного гиперболоида в канонической форме. Пусть, ради определенности, a 11 < 0, а 22 < 0, a 33 > 0, а 44 < 0. Тогда: (а 44 / a 11 ) > 0, (а 44 / a 22 ) > 0, (- а 44 / a 33 ) > 0 Обозначим эти числа соответственно через a 2, b 2, с2. После несложных преобразований уравнение (2) двуполостного гиперболоида можно записать в следующей форме:

(5) Уравнение (5) называется каноническим уравнением двуполостного гиперболоида. Если двуполостный гиперболоид задан своим (5) Уравнение (5) называется каноническим уравнением двуполостного гиперболоида. Если двуполостный гиперболоид задан своим каноническим уравнением, то оси Ох, Оу и Оz называются его главными осями.

4. Коэффициент а 44 равен нулю. В этом случае поверхность S называется конусом 4. Коэффициент а 44 равен нулю. В этом случае поверхность S называется конусом второго порядка. Если коэффициенты a 11 , а 22 , a 33 одного знака, то левая часть (2) обращается в нуль (а 44 = 0) лишь для х=у=z=0, т. е. уравнению поверхности S удовлетворяют координаты только одной точки. В этом случае поверхность S называется мнимым конусом второго порядка. Если коэффициенты a 11 , а 22 , a 33 имеют разные знаки, то поверхность S является вещественным конусом второго порядка. Обычно уравнение вещественного конуса второго порядка записывают в канонической форме. Пусть, ради определенности, a 11 > o, а 22 > 0, a 33 < 0. Обозначим соответственно через а 2, b 2, с2. Тогда уравнение (2) можно записать в виде

• (6) • Уравнение (6) называется каноническим уравнением вещественного конуса второго порядка. • (6) • Уравнение (6) называется каноническим уравнением вещественного конуса второго порядка.

Эллипсоиды Из уравнения (3) вытекает, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало Эллипсоиды Из уравнения (3) вытекает, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат — центром симметрии. Числа а, b, с называются полуосями эллипсоида и представляют собой длины отрезков, от начала координат до точек пересечения эллипсоида с осями координат. Чтобы более наглядно представить себе форму эллипсоида, выясним форму линий пересечения его плоскостями, параллельными какой-либо из координатных плоскостей. Ради определенности рассмотрим линии Lh пересечения эллипсоида с плоскостями z = h (7) параллельными плоскости Оху.

Уравнение проекции L*h линии Lh на плоскость Оху получается из уравнения (3), если Уравнение проекции L*h линии Lh на плоскость Оху получается из уравнения (3), если положить в нем z = h. Таким образом, уравнение этой проекции имеет вид (8) (9)

• Если (9) подставить в уравнение (8), то получим • (10) • т. • Если (9) подставить в уравнение (8), то получим • (10) • т. е. L*h представляет собой эллипс с полуосями а* и b*, которые могут быть вычислены по формулам (9). Так как Lh получается «подъемом» L*h на высоту h по оси Оz (7), то и Lh представляет собой эллипс.

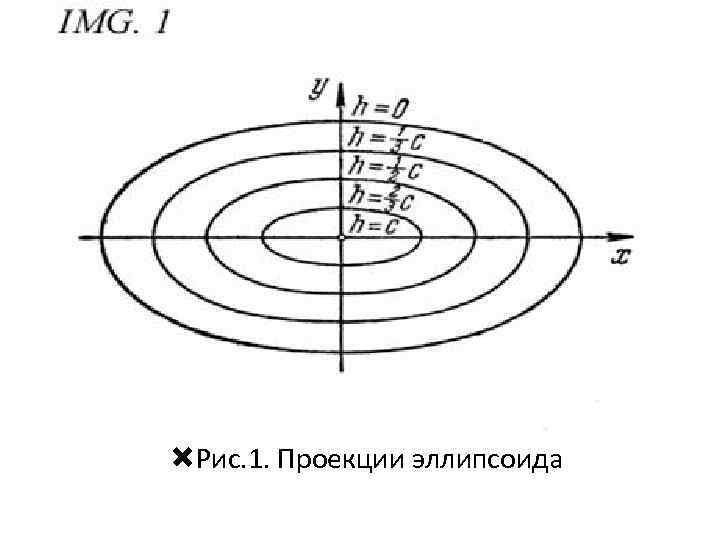Рис. 1. Проекции эллипсоида Рис. 1. Проекции эллипсоида

Представление об эллипсоиде можно получить следующим образом. Рассмотрим на плоскости Оху семейство эллипсов Представление об эллипсоиде можно получить следующим образом. Рассмотрим на плоскости Оху семейство эллипсов (10) (рис. 1), полуоси а* и b* которых зависят от h (9), и каждый такой эллипс снабдим отметкой h, указывающей, на какую высоту по оси Оz должен быть «поднят» этот эллипс. Мы получим своего рода «карту» эллипсоида. Используя эту «карту» , легко представить себе пространственный вид эллипсоида (рис. 2).

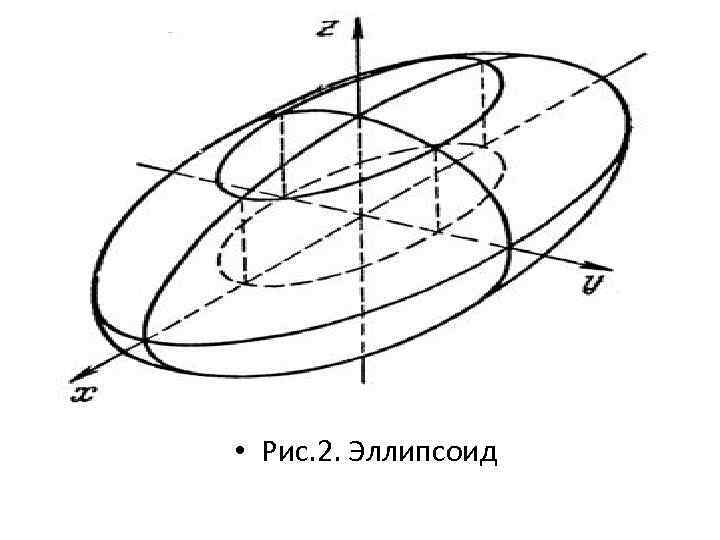• Рис. 2. Эллипсоид • Рис. 2. Эллипсоид

Построим поверхность, последовательно изображая полученные в сечениях эллипсы. На осях координат отмечаем точки, Построим поверхность, последовательно изображая полученные в сечениях эллипсы. На осях координат отмечаем точки, соответствующие полуосям. Начнем построение с изображения эллипса в плоскости Оху. Для удобства построим вспомогательный параллелограмм, в который впишем эллипс (рис. 3).

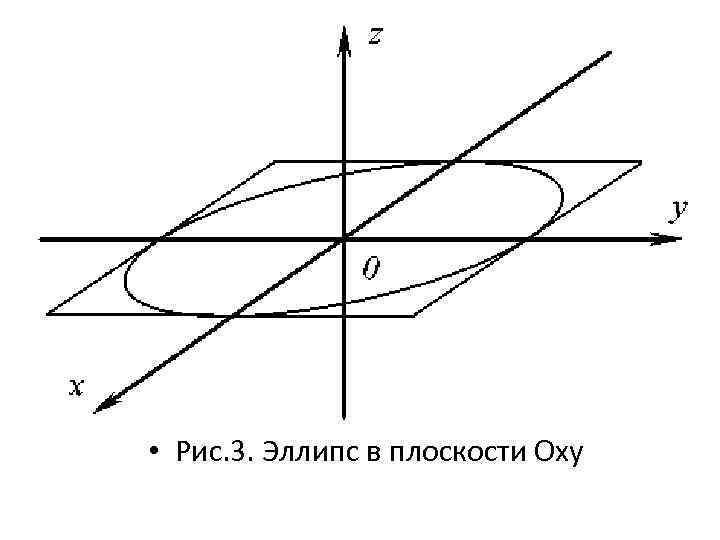• Рис. 3. Эллипс в плоскости Oxy • Рис. 3. Эллипс в плоскости Oxy

Уберем вспомогательный параллелограмм и по такой же схеме построим эллипс в плоскости Оxz (рис. Уберем вспомогательный параллелограмм и по такой же схеме построим эллипс в плоскости Оxz (рис. 4). • Рис. 4. Эллипс в плоскости Oxz

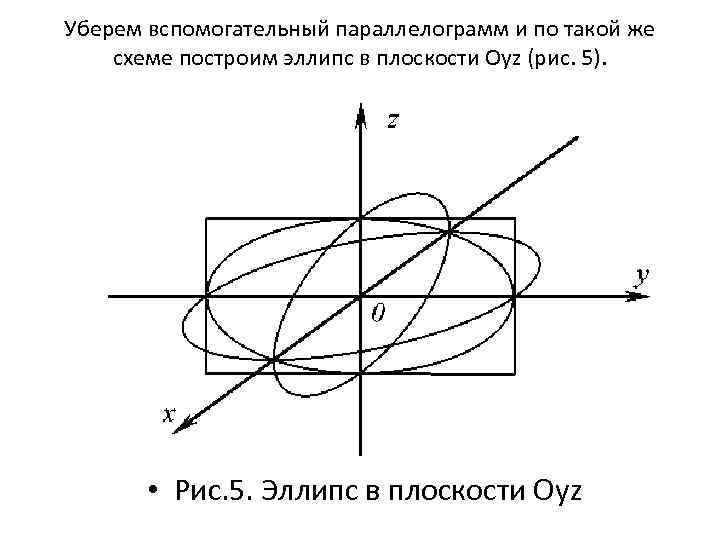Уберем вспомогательный параллелограмм и по такой же схеме построим эллипс в плоскости Oyz (рис. Уберем вспомогательный параллелограмм и по такой же схеме построим эллипс в плоскости Oyz (рис. 5). • Рис. 5. Эллипс в плоскости Oуz

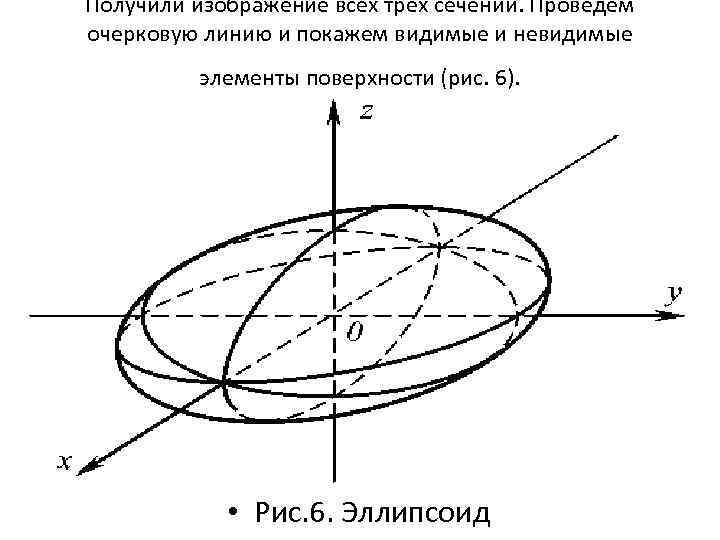Получили изображение всех трех сечений. Проведем очерковую линию и покажем видимые и невидимые элементы Получили изображение всех трех сечений. Проведем очерковую линию и покажем видимые и невидимые элементы поверхности (рис. 6). • Рис. 6. Эллипсоид

Образцы решения задач Пример 1. Выясним, какую поверхность в пространстве описывает уравнение x 2 Образцы решения задач Пример 1. Выясним, какую поверхность в пространстве описывает уравнение x 2 + y 2 + z 2 − 4 z = 0. Решение. Поскольку уравнение сдержит z 2 и z , необходимо выделить полный квадрат: x 2 + y 2 + (z − 2)2 = 4 и перейти к новой системе координат, полученной из исходной с помощью параллельного переноса так, что начало новой системы координат помещено в точку O'(0, 0, 2): x'2 + y'2 + z'2 = 4 где x' = x , y' = y и z' = z − 2. Получили каноническое уравнение сферы радиуса R=2. Ответ: сфера радиуса R = 2 с центром в точке O'(0, 0, 2).

Пример 2. Выяснить, какую поверхность в пространстве описывает уравнение x 2 + 2 Пример 2. Выяснить, какую поверхность в пространстве описывает уравнение x 2 + 2 x + 2 y 2 + 4 z 2 = 0. Решение. Поскольку уравнение сдержит x 2 и x , необходимо выделить полный квадрат: (x + 1)2 + 2 y 2 + 4 z 2 = 1 и перейти к новой системе координат, полученной из исходной с помощью параллельного переноса так, что начало новой системы координат помещено в точку O'(− 1, 0, 0): x'2 + 2 y'2 + 4 z'2 = 1 , где x' = x + 1 , y' = y и z' = z. Получили каноническое уравнение эллипсоида с полуосями a = 1 , b = 1/ и c = 1/2. Ответ: эллипсоид с центром в точке O'( − 1, 0, 0) и полуосями a = 1 , b = 1/ и c = 1/2.

Гиперболоиды Однополостный гиперболоид Обратимся к каноническому уравнению (4) однополостного гиперболоида. Из уравнения вытекает, что Гиперболоиды Однополостный гиперболоид Обратимся к каноническому уравнению (4) однополостного гиперболоида. Из уравнения вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида. Наименование «гиперболоид» (гиперболовидный) происходит от того, что среди сечений этой поверхности есть гиперболы. Они получаются при сечении данной поверхности плоскостями Oxz (y = 0) и Oyz (x = 0) (главные сечения). Сечение однополостного гиперболоида всякой плоскостью Oxy, (z = h) есть эллипс.

• Сечение плоскостью Oxy, (z = 0) есть эллипс, который называется горловым эллипсом. • Сечение плоскостью Oxy, (z = 0) есть эллипс, который называется горловым эллипсом. При a = b эллипсы обращаются в окружности, а однополостный гиперболоид – в однополостный гиперболоид вращения. • • – однополостный гиперболоид с осью Oz.

Построим поверхность, последовательно изображая полученные в сечениях гиперболы и эллипсы. Начнем построение с Построим поверхность, последовательно изображая полученные в сечениях гиперболы и эллипсы. Начнем построение с изображения гиперболы в плоскости Oxz, где a – действительная полуось и с – мнимая полуось. Выберем произвольную высоту однополостного гиперболоида h, проведем прямые параллельные оси Оx, получим плоскость, образованную данной гиперболой (рис. 7).

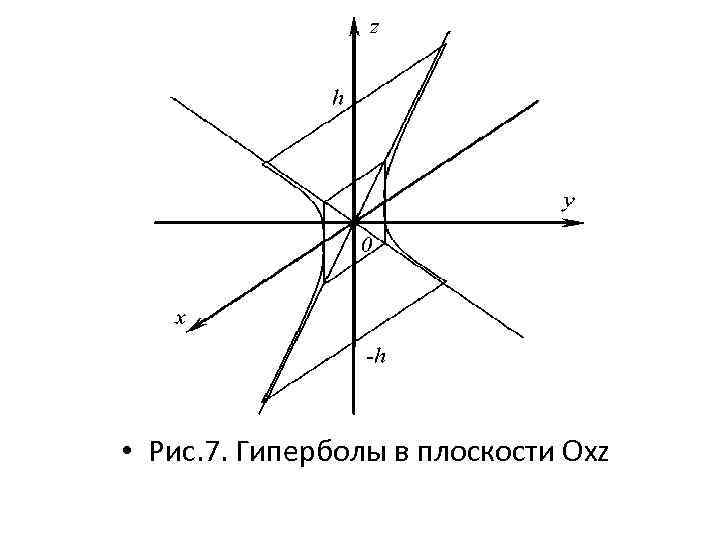• Рис. 7. Гиперболы в плоскости Oxz • Рис. 7. Гиперболы в плоскости Oxz

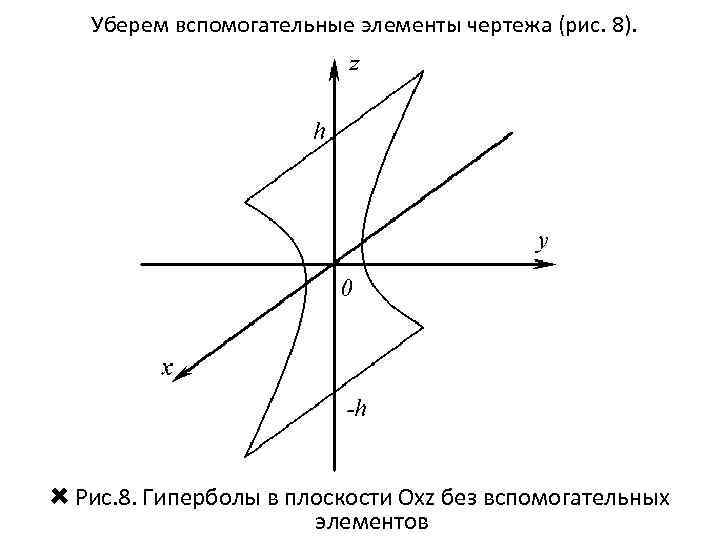Уберем вспомогательные элементы чертежа (рис. 8). Рис. 8. Гиперболы в плоскости Oxz без вспомогательных Уберем вспомогательные элементы чертежа (рис. 8). Рис. 8. Гиперболы в плоскости Oxz без вспомогательных элементов

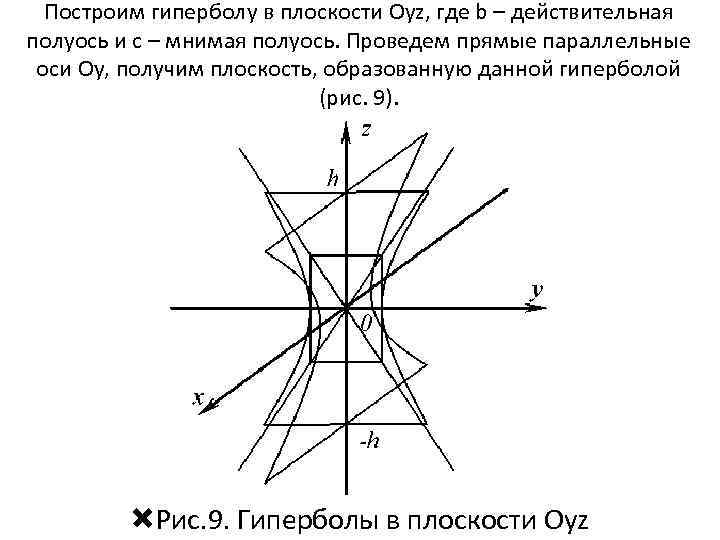Построим гиперболу в плоскости Oyz, где b – действительная полуось и с – мнимая Построим гиперболу в плоскости Oyz, где b – действительная полуось и с – мнимая полуось. Проведем прямые параллельные оси Оy, получим плоскость, образованную данной гиперболой (рис. 9). Рис. 9. Гиперболы в плоскости Oyz

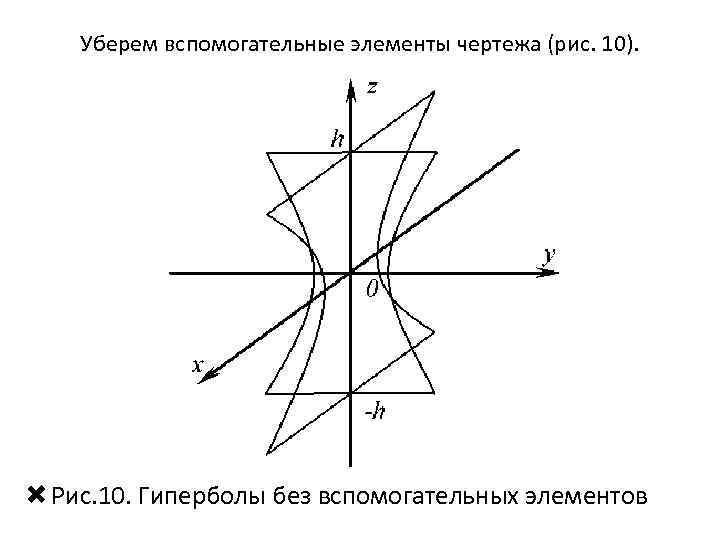Уберем вспомогательные элементы чертежа (рис. 10). Рис. 10. Гиперболы без вспомогательных элементов Уберем вспомогательные элементы чертежа (рис. 10). Рис. 10. Гиперболы без вспомогательных элементов

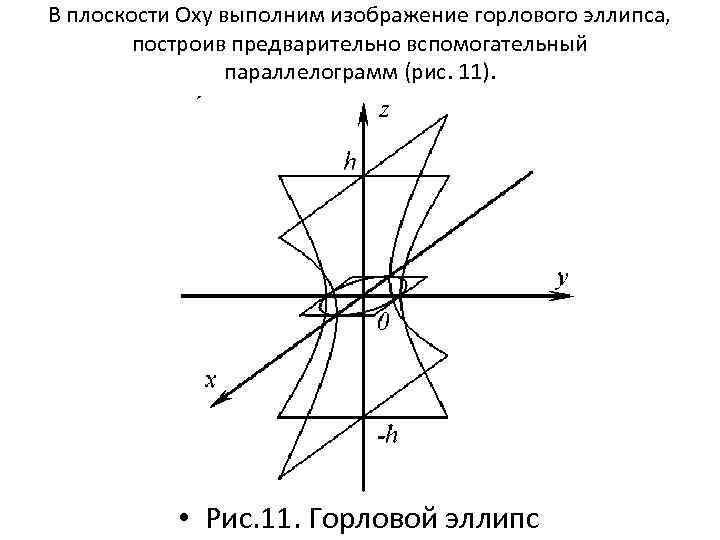В плоскости Oxy выполним изображение горлового эллипса, построив предварительно вспомогательный параллелограмм (рис. 11). • В плоскости Oxy выполним изображение горлового эллипса, построив предварительно вспомогательный параллелограмм (рис. 11). • Рис. 11. Горловой эллипс

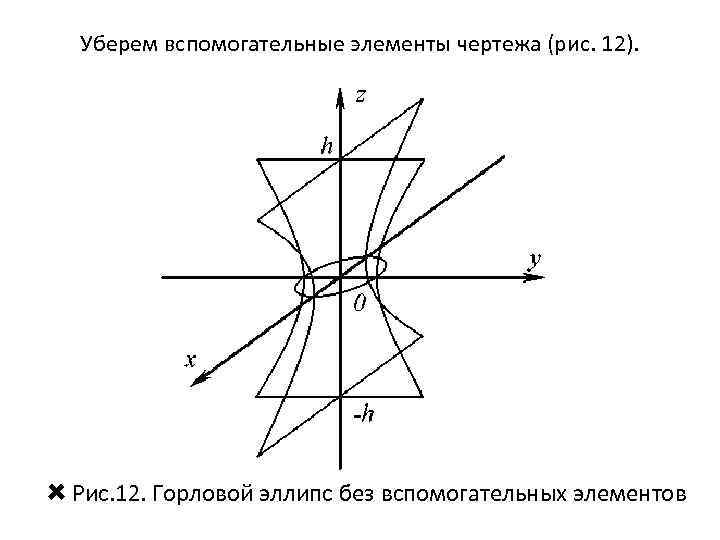Уберем вспомогательные элементы чертежа (рис. 12). Рис. 12. Горловой эллипс без вспомогательных элементов Уберем вспомогательные элементы чертежа (рис. 12). Рис. 12. Горловой эллипс без вспомогательных элементов

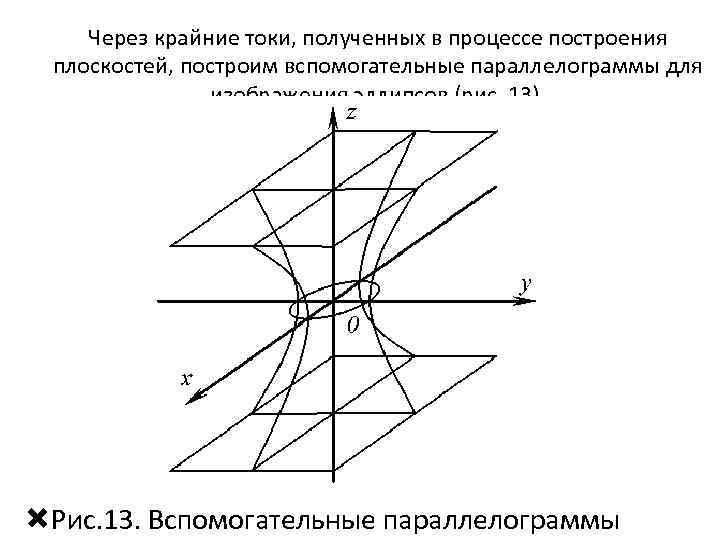Через крайние токи, полученных в процессе построения плоскостей, построим вспомогательные параллелограммы для изображения эллипсов Через крайние токи, полученных в процессе построения плоскостей, построим вспомогательные параллелограммы для изображения эллипсов (рис. 13). Рис. 13. Вспомогательные параллелограммы

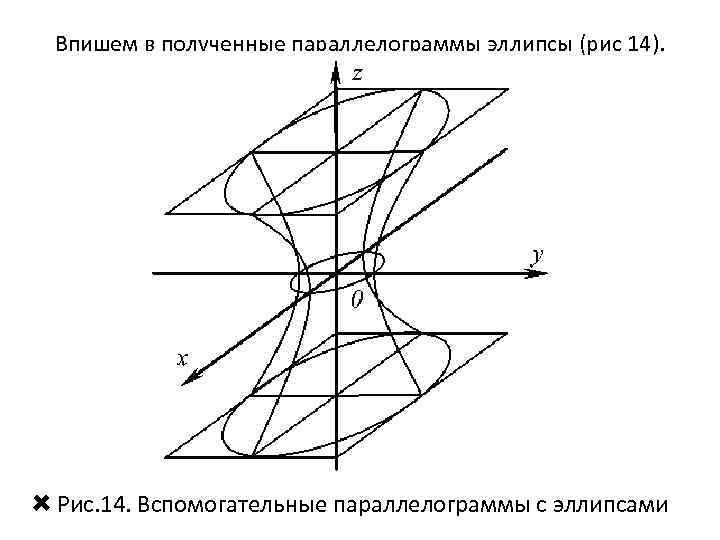Впишем в полученные параллелограммы эллипсы (рис 14). Рис. 14. Вспомогательные параллелограммы с эллипсами Впишем в полученные параллелограммы эллипсы (рис 14). Рис. 14. Вспомогательные параллелограммы с эллипсами

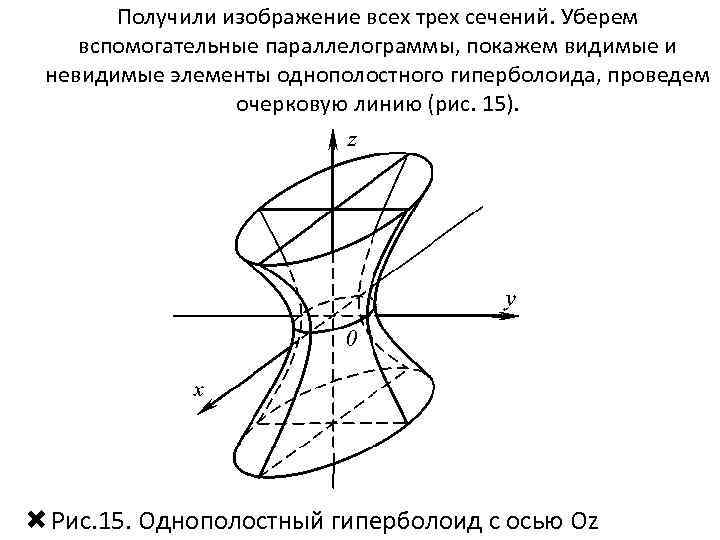Получили изображение всех трех сечений. Уберем вспомогательные параллелограммы, покажем видимые и невидимые элементы однополостного Получили изображение всех трех сечений. Уберем вспомогательные параллелограммы, покажем видимые и невидимые элементы однополостного гиперболоида, проведем очерковую линию (рис. 15). Рис. 15. Однополостный гиперболоид с осью Oz

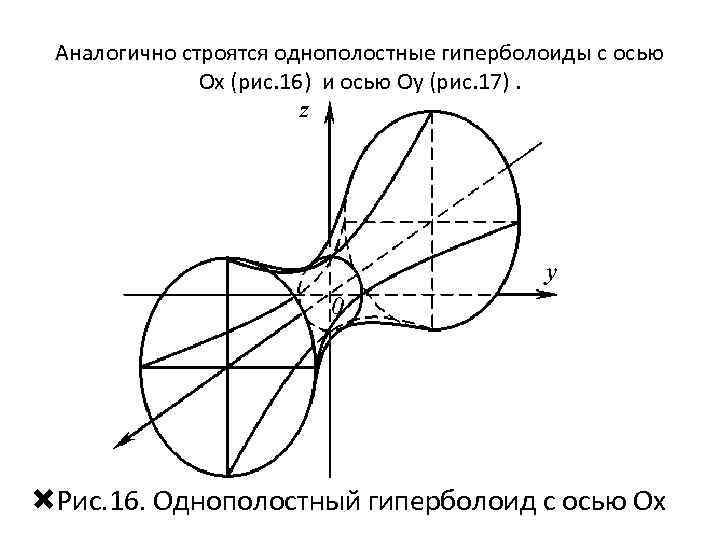Аналогично строятся однополостные гиперболоиды с осью Oх (рис. 16) и осью Оу (рис. 17). Аналогично строятся однополостные гиперболоиды с осью Oх (рис. 16) и осью Оу (рис. 17). Рис. 16. Однополостный гиперболоид с осью Oх

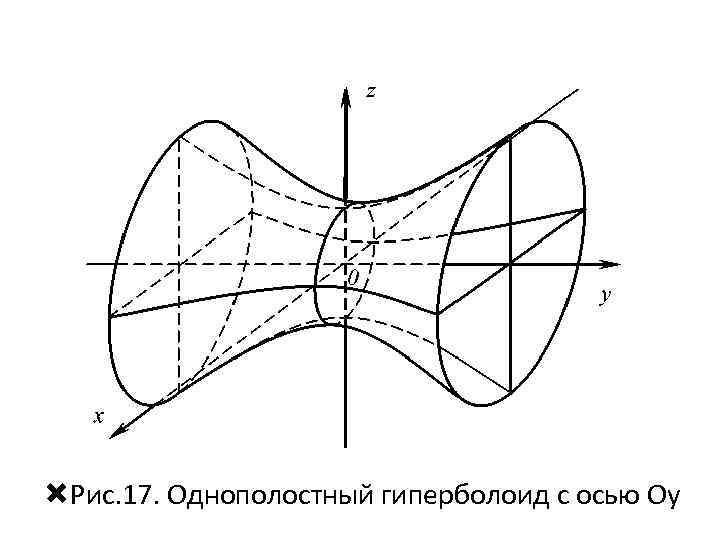Рис. 17. Однополостный гиперболоид с осью Oу Рис. 17. Однополостный гиперболоид с осью Oу

Двуполостный гиперболоид Из канонического уравнения (5) двуполостного гиперболоида вытекает, что координатные плоскости являются Двуполостный гиперболоид Из канонического уравнения (5) двуполостного гиперболоида вытекает, что координатные плоскости являются его плоскостями симметрии, а начало координат — его центром симметрии. Данная поверхность получила свое название изза того, что она состоит из двух разобщенных полостей, образованных гиперболами с действительной осью Oz. В плоскости Oxy в сечении получаем мнимый эллипс. При z = h (h > с) в каждом сечении будет эллипс. Плоскость Oxz: в сечении получили гиперболу. В плоскости Oyz в сечении получаем гиперболу.

• Построим поверхность, последовательно изображая полученные в сечениях гиперболы и эллипсы. • Начнем • Построим поверхность, последовательно изображая полученные в сечениях гиперболы и эллипсы. • Начнем построение с изображения гиперболы в плоскости Oxz, где c – действительная полуось и a – мнимая полуось. Выберем произвольную высоту однополостного гиперболоида h, проведем прямые параллельные оси Оx, получим плоскость, образованную данной гиперболой (рис. 18).

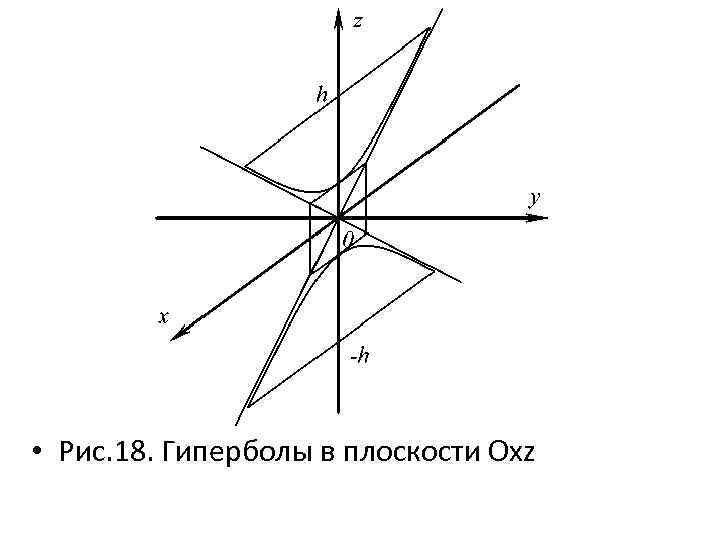• Рис. 18. Гиперболы в плоскости Oxz • Рис. 18. Гиперболы в плоскости Oxz

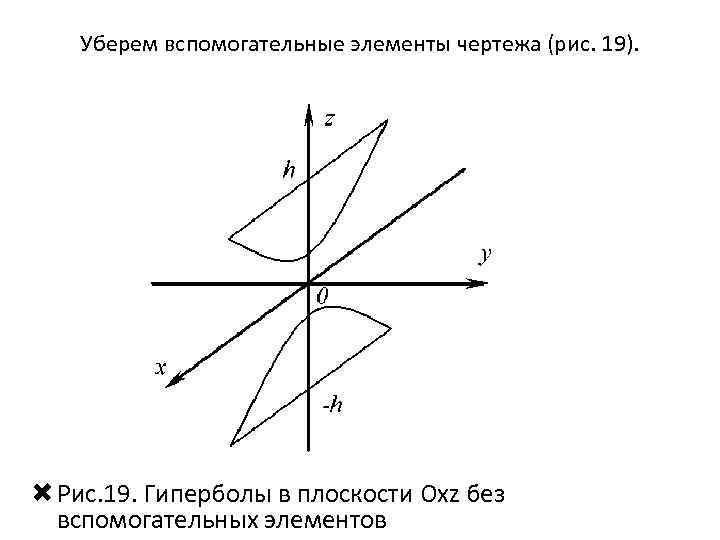Уберем вспомогательные элементы чертежа (рис. 19). Рис. 19. Гиперболы в плоскости Oxz без вспомогательных Уберем вспомогательные элементы чертежа (рис. 19). Рис. 19. Гиперболы в плоскости Oxz без вспомогательных элементов

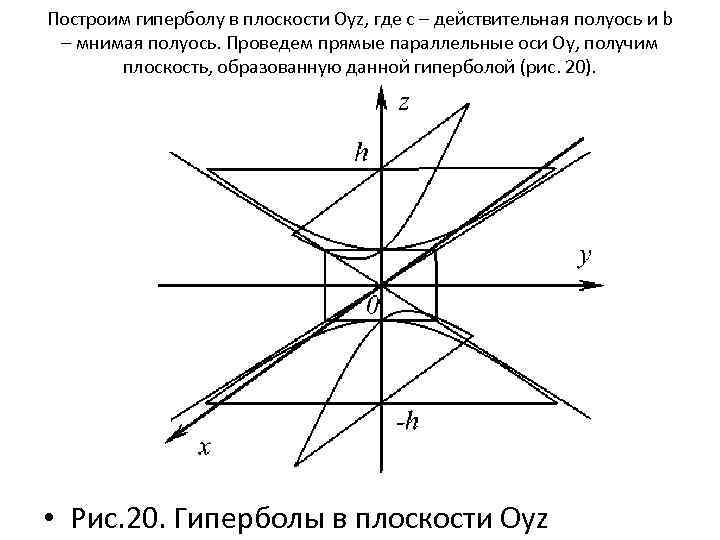Построим гиперболу в плоскости Oyz, где с – действительная полуось и b – мнимая Построим гиперболу в плоскости Oyz, где с – действительная полуось и b – мнимая полуось. Проведем прямые параллельные оси Оy, получим плоскость, образованную данной гиперболой (рис. 20). • Рис. 20. Гиперболы в плоскости Oуz

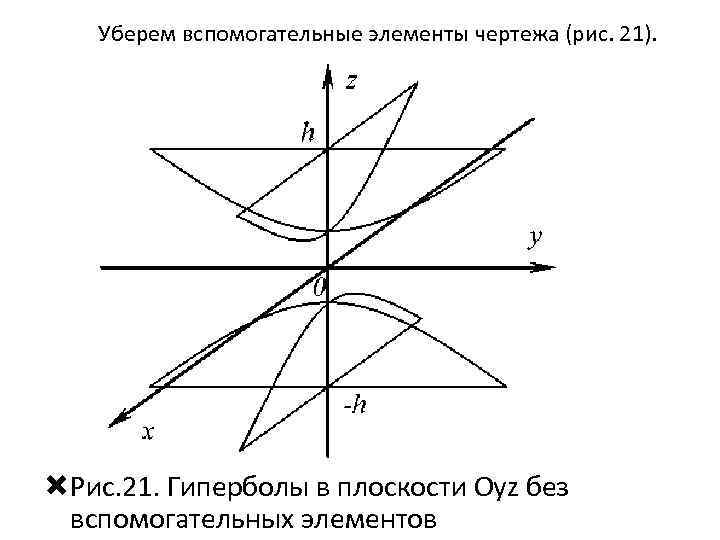Уберем вспомогательные элементы чертежа (рис. 21). Рис. 21. Гиперболы в плоскости Oуz без вспомогательных Уберем вспомогательные элементы чертежа (рис. 21). Рис. 21. Гиперболы в плоскости Oуz без вспомогательных элементов

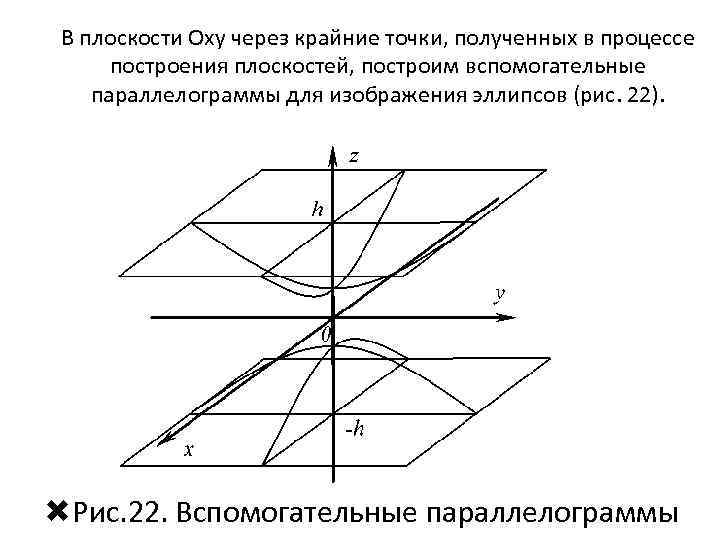В плоскости Oxy через крайние точки, полученных в процессе построения плоскостей, построим вспомогательные параллелограммы В плоскости Oxy через крайние точки, полученных в процессе построения плоскостей, построим вспомогательные параллелограммы для изображения эллипсов (рис. 22). Рис. 22. Вспомогательные параллелограммы

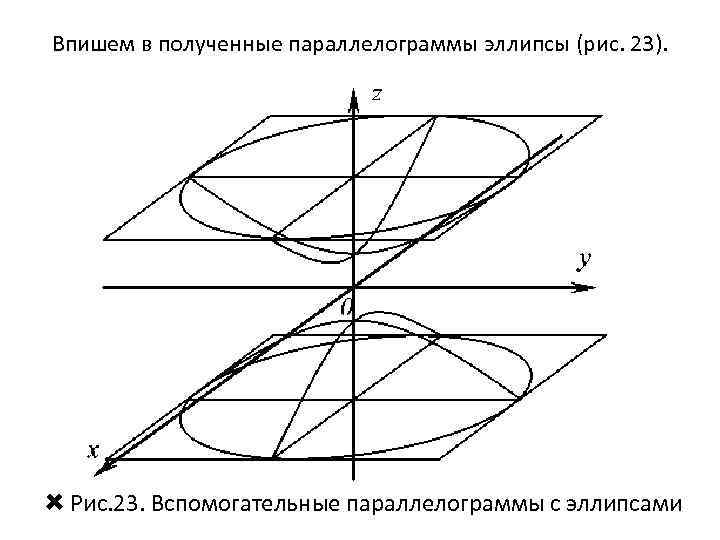Впишем в полученные параллелограммы эллипсы (рис. 23). Рис. 23. Вспомогательные параллелограммы с эллипсами Впишем в полученные параллелограммы эллипсы (рис. 23). Рис. 23. Вспомогательные параллелограммы с эллипсами

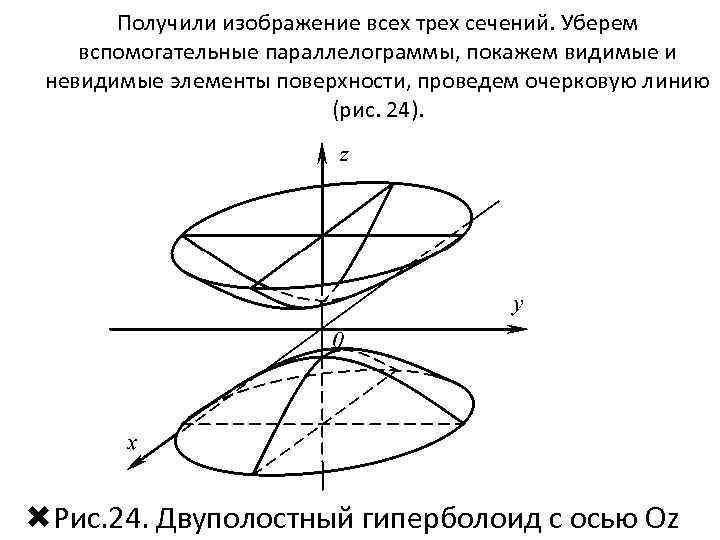Получили изображение всех трех сечений. Уберем вспомогательные параллелограммы, покажем видимые и невидимые элементы поверхности, Получили изображение всех трех сечений. Уберем вспомогательные параллелограммы, покажем видимые и невидимые элементы поверхности, проведем очерковую линию (рис. 24). Рис. 24. Двуполостный гиперболоид с осью Oz

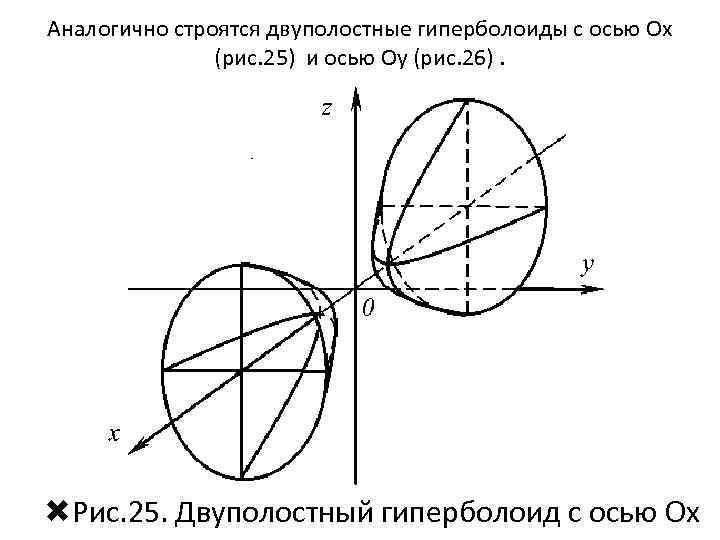Аналогично строятся двуполостные гиперболоиды с осью Oх (рис. 25) и осью Оу (рис. 26). Аналогично строятся двуполостные гиперболоиды с осью Oх (рис. 25) и осью Оу (рис. 26). Рис. 25. Двуполостный гиперболоид с осью Oх

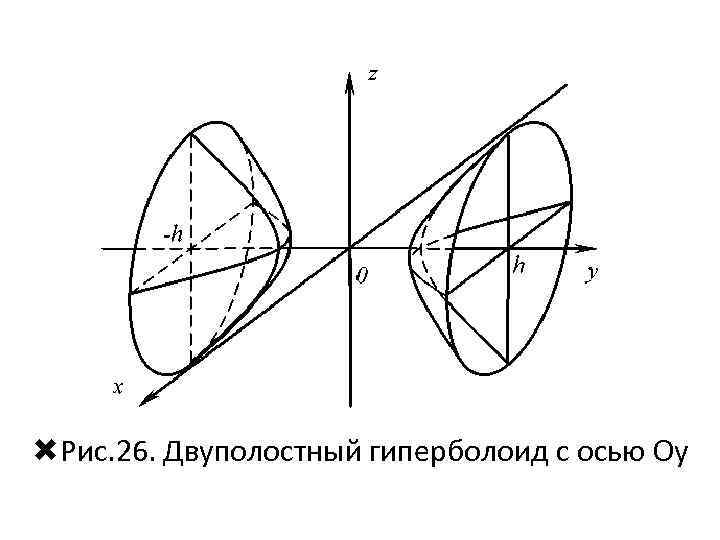Рис. 26. Двуполостный гиперболоид с осью Oу Рис. 26. Двуполостный гиперболоид с осью Oу

Образцы решения задач Пример 1. Выясним, какую поверхность в пространстве описывает уравнение x 2 Образцы решения задач Пример 1. Выясним, какую поверхность в пространстве описывает уравнение x 2 + 2 x − 2 y 2 + 4 z 2 = 0. Решение. Поскольку уравнение сдержит x 2 и x , необходимо выделить полный квадрат: (x + 1)2 − 2 y 2 + 4 z 2 = 1 и перейти к новой системе координат, полученной из исходной с помощью параллельного переноса так, что начало новой системы координат помещено в точку O'(− 1, 0, 0): x'2 − 2 y'2 + 4 z'2 = 1 , где x' = x + 1 , y' = y и z' = z. Получили каноническое уравнение однополостного гиперболоида с полуосями a = 1 , b = 1/ и c = 1/2. Ответ: однополостный гиперболоид с осью симметрии, параллельной оси OY, и полуосями a = 1 , b = 1/ и c = 1/2.

Пример 2. Выясним, какую поверхность в пространстве описывает уравнение Решение. Поскольку уравнение сдержит Пример 2. Выясним, какую поверхность в пространстве описывает уравнение Решение. Поскольку уравнение сдержит корень, необходимо возвести обе части уравнения в квадрат (при этом мы приобретаем "лишние" решения и, следовательно, "лишние" точки). Имеем: x 2 − y 2 − z 2 = 1. Используя метод сечений, легко убедиться, что это двуполостный гиперболоид, осью которого является ось OX. Следовательно, исходное уравнение описывает половину этой поверхности ( x ≥ 0 ).

Параболоиды Эллиптический параболоид Обращаясь к каноническому уравнению (11) эллиптического параболоида (11) мы видим, что Параболоиды Эллиптический параболоид Обращаясь к каноническому уравнению (11) эллиптического параболоида (11) мы видим, что для него Oxz и Оуz являются плоскостями симметрии. Ось Oz, представляющая линию пересечения этих плоскостей, называется осью эллиптического параболоида.

• Наименование «параболоид» происходит от того, что среди сечений этой поверхности есть параболы. • Наименование «параболоид» происходит от того, что среди сечений этой поверхности есть параболы. Они получаются при сечении данной поверхности плоскостями Oxz (y = 0) и Oyz (x = 0) (главные сечения). • Рассмотрим построение эллиптических параболоидов с разными осями. • – эллиптический параболоид с осью Oz.

В плоскости Oxy в сечении получаем пару мнимых прямых, пересекающихся в начале координат. В плоскости Oxy в сечении получаем пару мнимых прямых, пересекающихся в начале координат. При z = h (h > 0) в каждом сечении будет эллипс. Плоскость Oxz: в сечении получили параболу. Плоскость Oyz: в сечении получили параболу. Построим поверхность, последовательно изображая полученные в сечениях параболы и эллипс. Начнем построение с изображения параболы в плоскости Oxz. Выберем произвольную высоту эллиптического параболоида h, проведем прямую параллельную оси Оx, получим плоскость, образованную данной параболой (рис. 27).

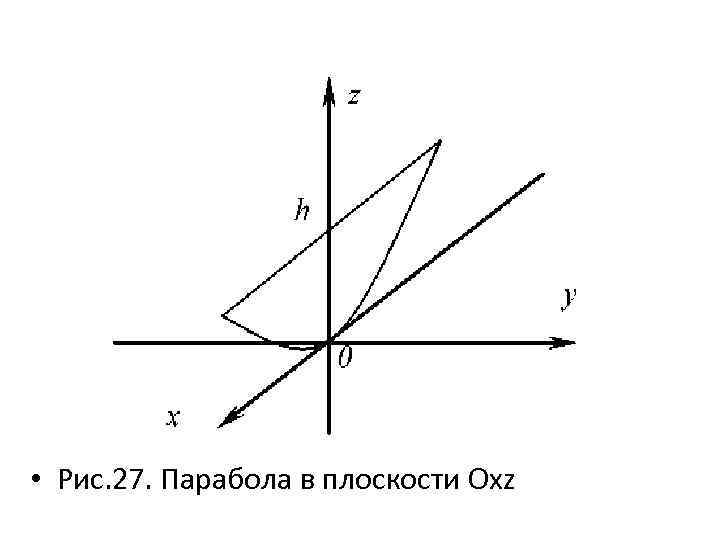• Рис. 27. Парабола в плоскости Oxz • Рис. 27. Парабола в плоскости Oxz

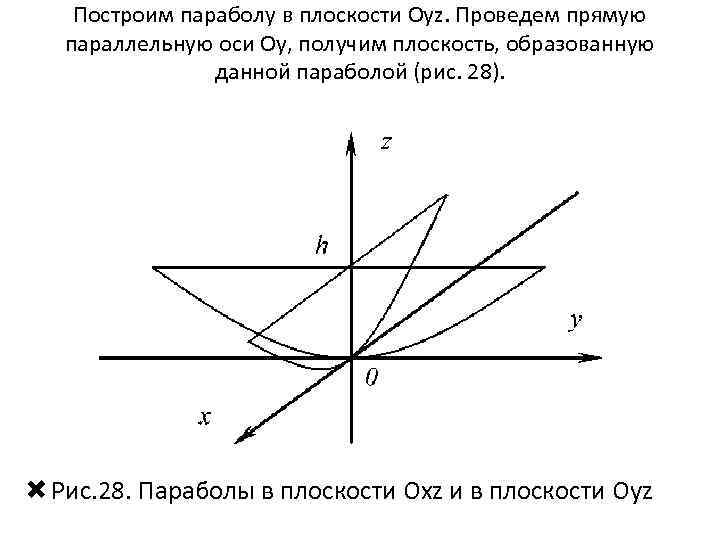Построим параболу в плоскости Oyz. Проведем прямую параллельную оси Оy, получим плоскость, образованную данной Построим параболу в плоскости Oyz. Проведем прямую параллельную оси Оy, получим плоскость, образованную данной параболой (рис. 28). Рис. 28. Параболы в плоскости Oxz и в плоскости Oyz

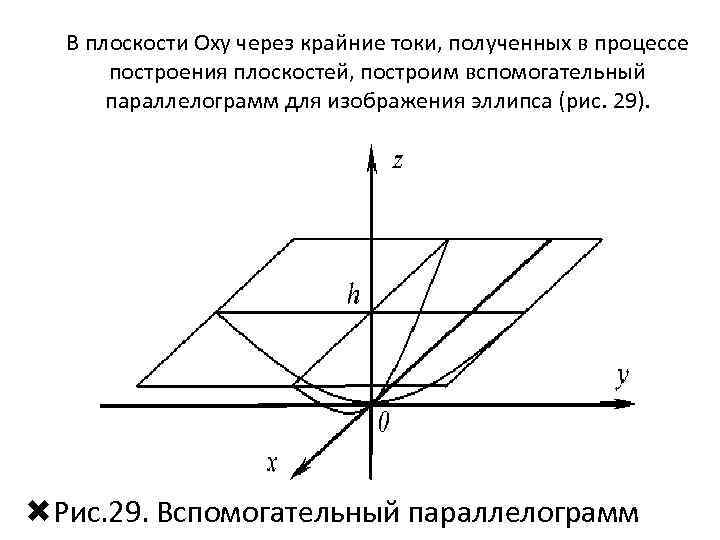В плоскости Oxy через крайние токи, полученных в процессе построения плоскостей, построим вспомогательный параллелограмм В плоскости Oxy через крайние токи, полученных в процессе построения плоскостей, построим вспомогательный параллелограмм для изображения эллипса (рис. 29). Рис. 29. Вспомогательный параллелограмм

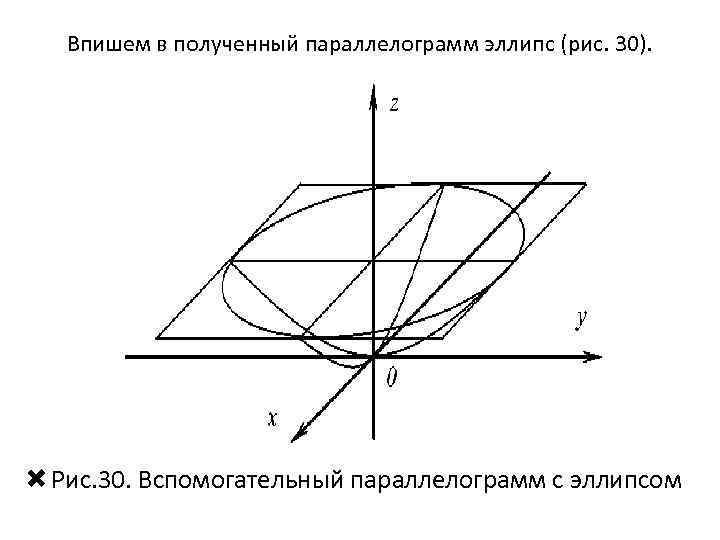Впишем в полученный параллелограмм эллипс (рис. 30). Рис. 30. Вспомогательный параллелограмм с эллипсом Впишем в полученный параллелограмм эллипс (рис. 30). Рис. 30. Вспомогательный параллелограмм с эллипсом

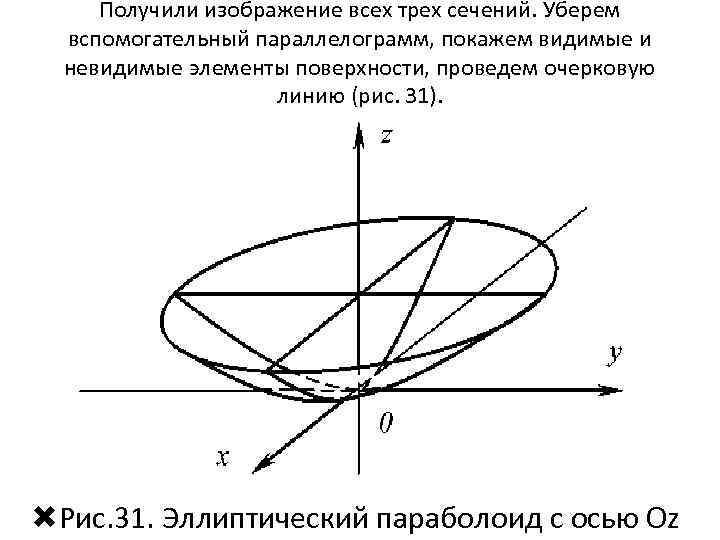Получили изображение всех трех сечений. Уберем вспомогательный параллелограмм, покажем видимые и невидимые элементы поверхности, Получили изображение всех трех сечений. Уберем вспомогательный параллелограмм, покажем видимые и невидимые элементы поверхности, проведем очерковую линию (рис. 31). Рис. 31. Эллиптический параболоид с осью Oz

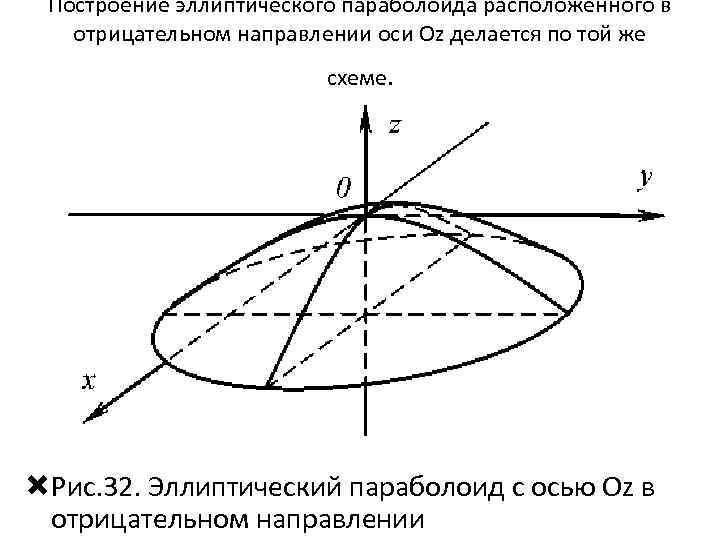Построение эллиптического параболоида расположенного в отрицательном направлении оси Oz делается по той же схеме. Построение эллиптического параболоида расположенного в отрицательном направлении оси Oz делается по той же схеме. Рис. 32. Эллиптический параболоид с осью Oz в отрицательном направлении

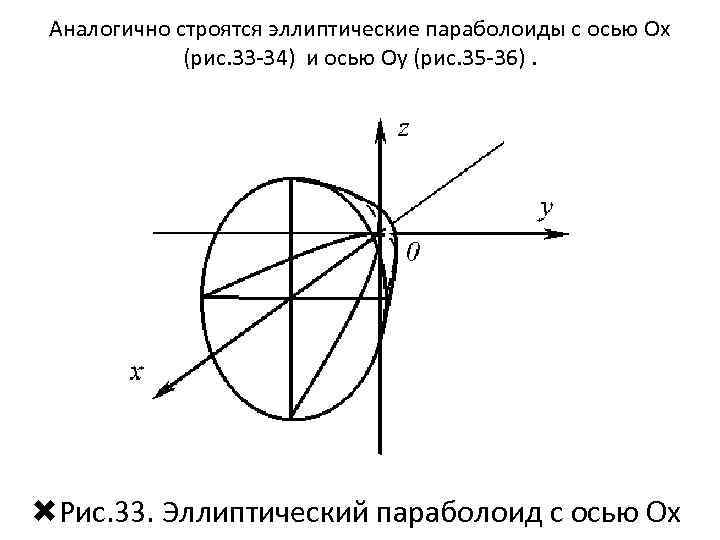Аналогично строятся эллиптические параболоиды с осью Oх (рис. 33 -34) и осью Оу (рис. Аналогично строятся эллиптические параболоиды с осью Oх (рис. 33 -34) и осью Оу (рис. 35 -36). Рис. 33. Эллиптический параболоид с осью Oх

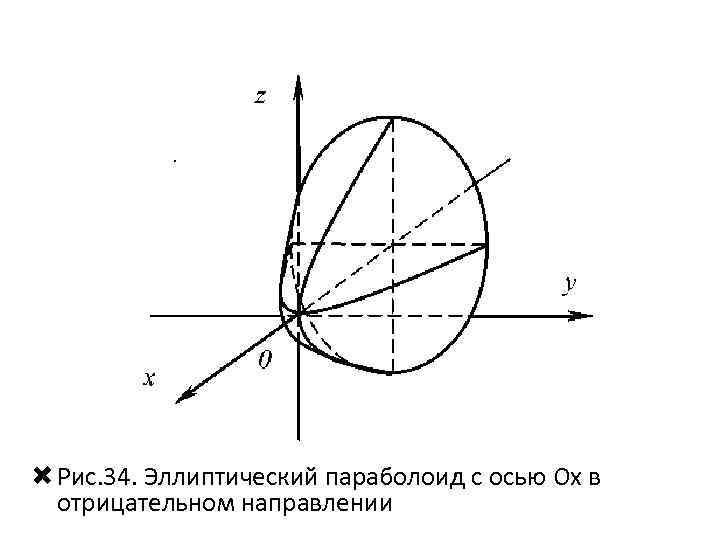Рис. 34. Эллиптический параболоид с осью Oх в отрицательном направлении Рис. 34. Эллиптический параболоид с осью Oх в отрицательном направлении

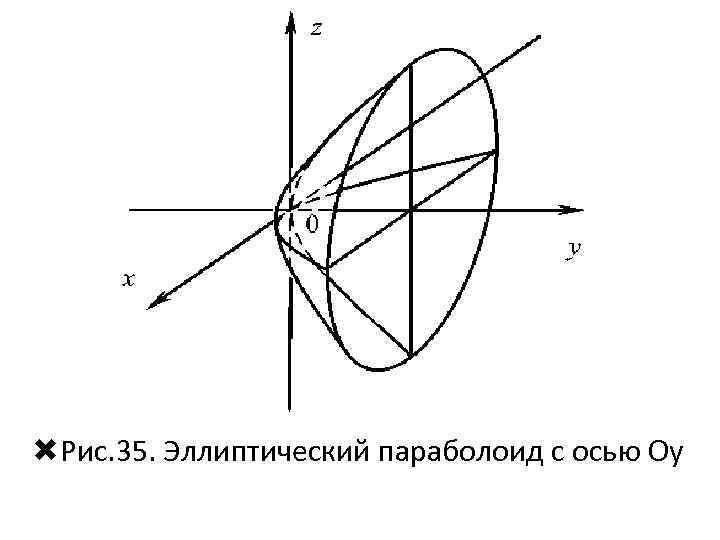Рис. 35. Эллиптический параболоид с осью Oу Рис. 35. Эллиптический параболоид с осью Oу

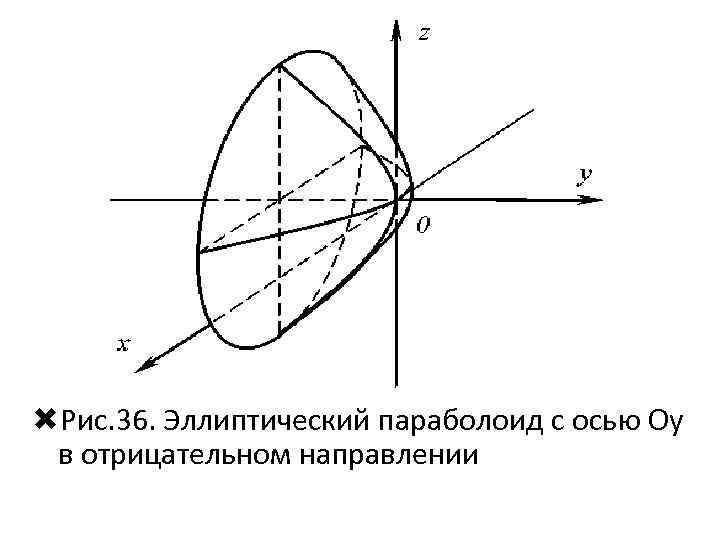Рис. 36. Эллиптический параболоид с осью Oу в отрицательном направлении Рис. 36. Эллиптический параболоид с осью Oу в отрицательном направлении

• Гиперболический параболоид • (12) • Из канонического уравнения (12) гиперболического параболоида вытекает, • Гиперболический параболоид • (12) • Из канонического уравнения (12) гиперболического параболоида вытекает, что плоскости Oxz и Оуz являются плоскостями симметрии. Ось Oz называется осью гиперболического пaраболоида.

Линии z=h пересечения гиперболического параболоида плоскостями z=h представляют собой при h>0 гиперболы (13) Линии z=h пересечения гиперболического параболоида плоскостями z=h представляют собой при h>0 гиперболы (13) с полуосями (14) (15) при h < 0 - сопряженными гиперболами для гипербол (13) являются (14) с полуосями

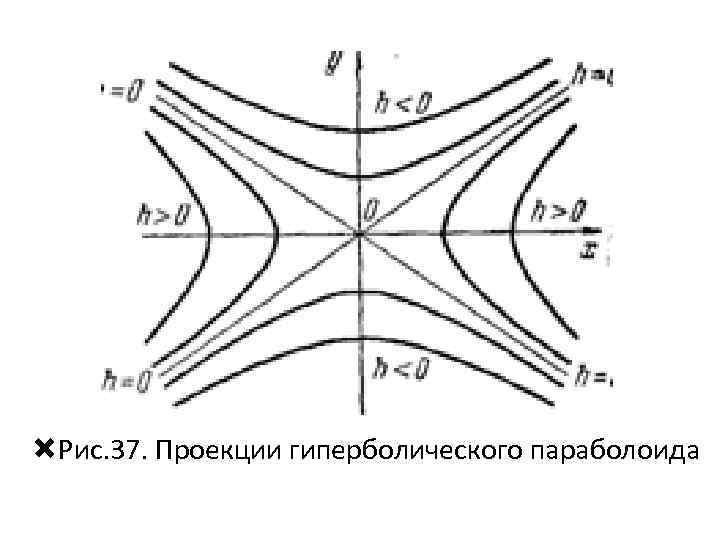Рис. 37. Проекции гиперболического параболоида Рис. 37. Проекции гиперболического параболоида

• Используя формулы (14)—(16), легко построить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 • Используя формулы (14)—(16), легко построить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым: из формул (14) и (16) вытекает, что прямые (16) являются асимптотами гипербол (13) и (15).

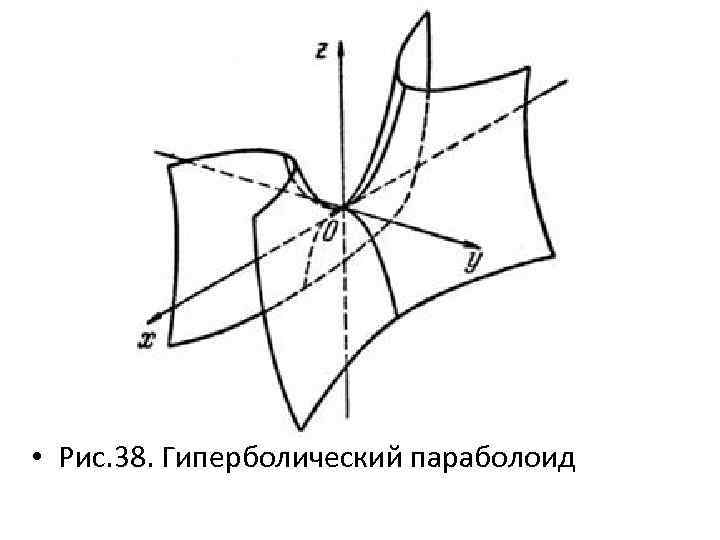• Рис. 38. Гиперболический параболоид • Рис. 38. Гиперболический параболоид

В противоположность главным сечениям эллиптического параболоида параболы обращены вогнутостями в противоположные стороны (парабола В противоположность главным сечениям эллиптического параболоида параболы обращены вогнутостями в противоположные стороны (парабола в плоскости Oxz – ветвями вверх, называется неподвижной параболой, парабола в плоскости Oyz – ветвями вниз, называется подвижной или скользящей параболой).

• Замечание. Ни при каких значениях a и b гиперболический параболоид (в отличие • Замечание. Ни при каких значениях a и b гиперболический параболоид (в отличие от вышерассмотренных поверхностей второго порядка) не является поверхностью вращения.

Рассмотрим построение гиперболических параболоидов с разными осями. 1. а) – эллиптический параболоид с Рассмотрим построение гиперболических параболоидов с разными осями. 1. а) – эллиптический параболоид с осью Oz. Плоскость Oxy: в сечении получили пару прямых, пересекающихся в начале координат. При z = h (h < 0) в каждом сечении будет гипербола с действительной осью Oy. Плоскость Oxz: в сечении получили параболу. Плоскость Oyz: в сечении получили параболу. Построим поверхность, последовательно изображая полученные в сечениях параболы и гиперболу. Начнем построение с изображения неподвижной параболы в плоскости Oxz (рис. 39).

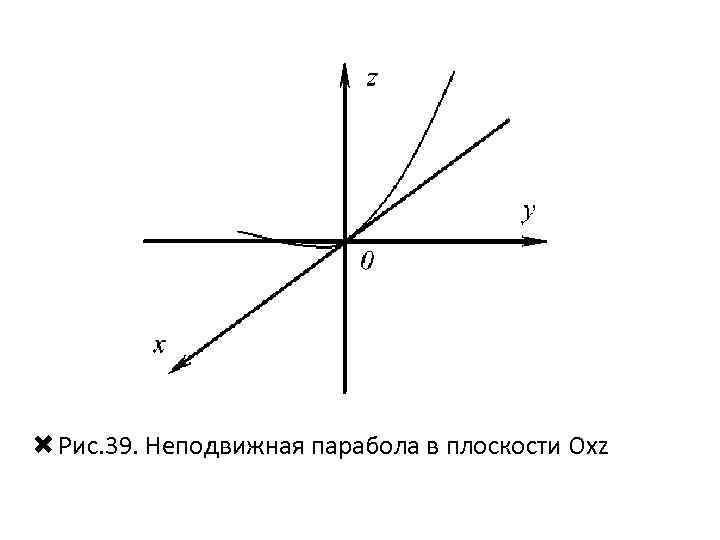Рис. 39. Неподвижная парабола в плоскости Oxz Рис. 39. Неподвижная парабола в плоскости Oxz

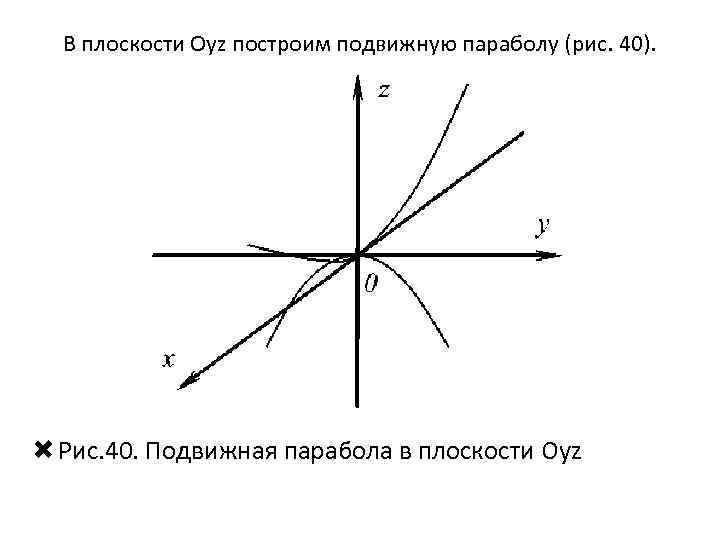В плоскости Oyz построим подвижную параболу (рис. 40). Рис. 40. Подвижная парабола в плоскости В плоскости Oyz построим подвижную параболу (рис. 40). Рис. 40. Подвижная парабола в плоскости Oуz

• Выберем произвольную высоту гиперболического параболоида –h и подставим ее значение в соответствующее • Выберем произвольную высоту гиперболического параболоида –h и подставим ее значение в соответствующее уравнение. Для изображения гиперболы с действительной осью Oy построим вспомогательную систему координат Oх с центром в точке с координатами (0; 0; –h) (рис. 41).

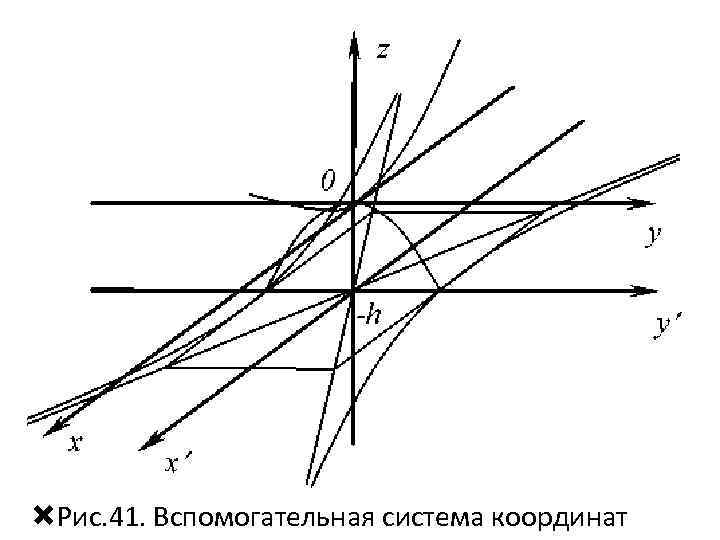Рис. 41. Вспомогательная система координат Рис. 41. Вспомогательная система координат

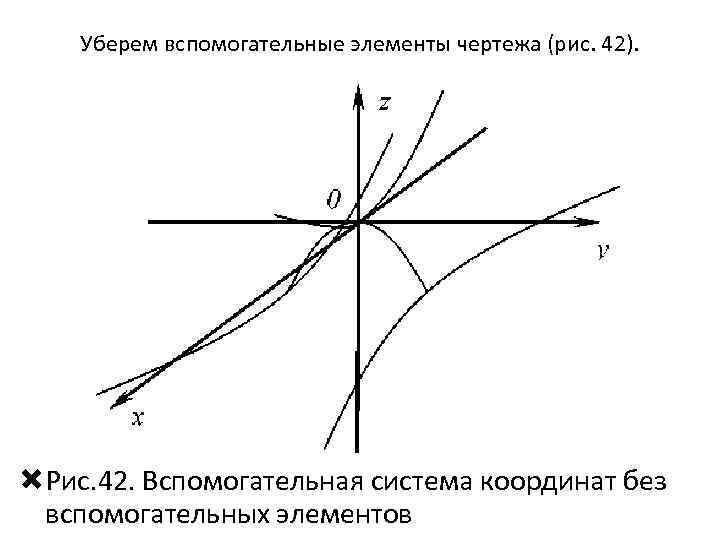Уберем вспомогательные элементы чертежа (рис. 42). Рис. 42. Вспомогательная система координат без вспомогательных элементов Уберем вспомогательные элементы чертежа (рис. 42). Рис. 42. Вспомогательная система координат без вспомогательных элементов

• Переместим подвижную параболу в крайние точки неподвижной параболы и опустим соответствующие ветви • Переместим подвижную параболу в крайние точки неподвижной параболы и опустим соответствующие ветви полученных в результате преобразования парабол на гиперболу (рис. 43)

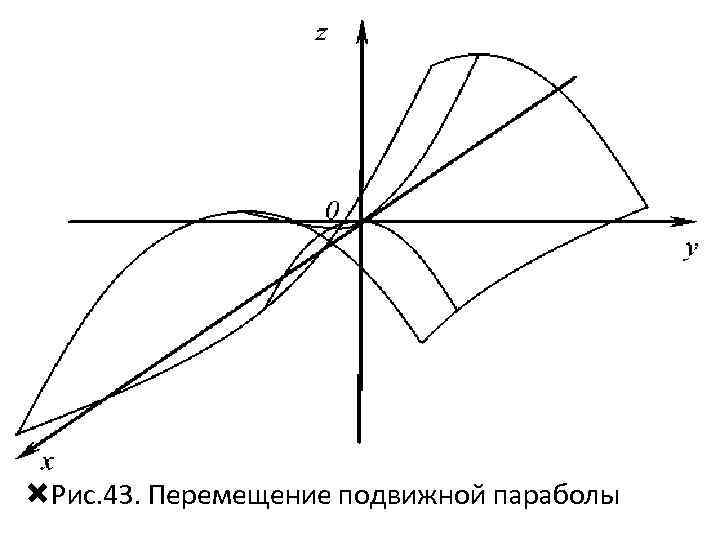Рис. 43. Перемещение подвижной параболы Рис. 43. Перемещение подвижной параболы

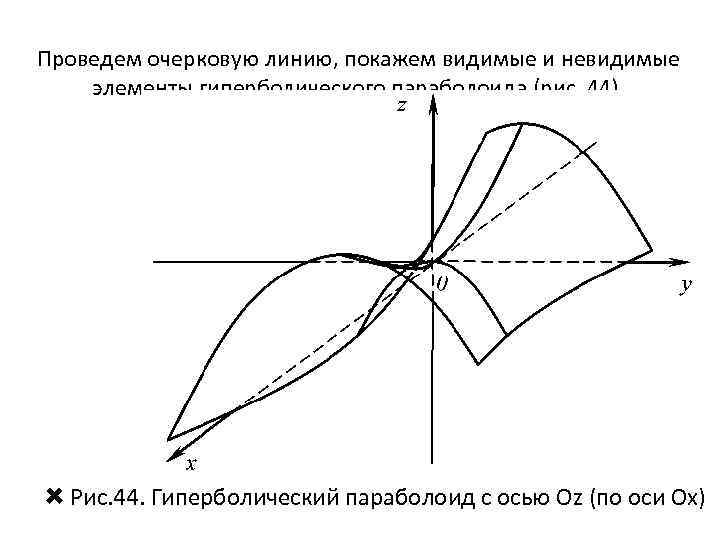Проведем очерковую линию, покажем видимые и невидимые элементы гиперболического параболоида (рис. 44). Рис. 44. Проведем очерковую линию, покажем видимые и невидимые элементы гиперболического параболоида (рис. 44). Рис. 44. Гиперболический параболоид с осью Oz (по оси Ох)

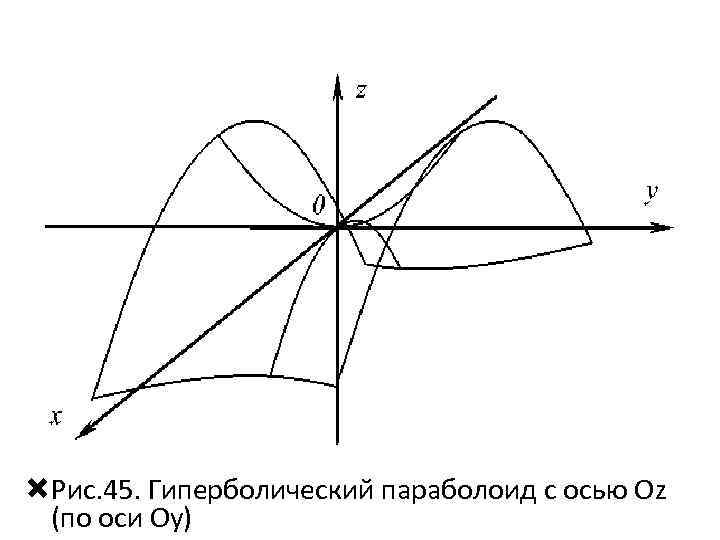Рис. 45. Гиперболический параболоид с осью Oz (по оси Оу) Рис. 45. Гиперболический параболоид с осью Oz (по оси Оу)

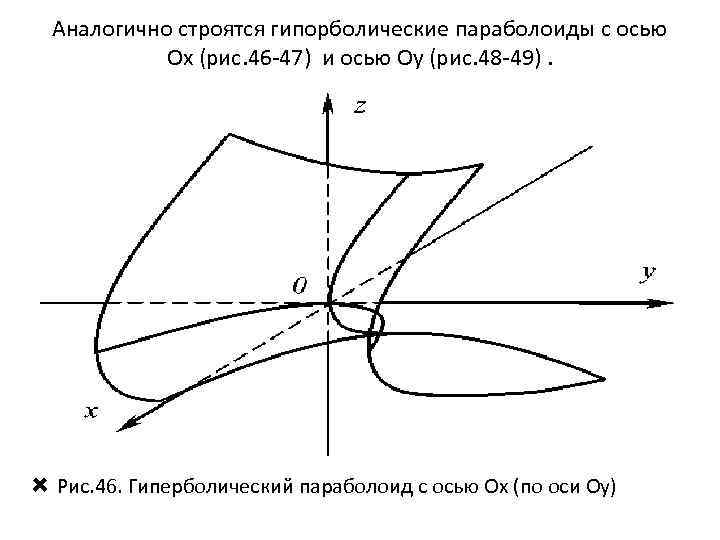Аналогично строятся гипорболические параболоиды с осью Oх (рис. 46 -47) и осью Оу (рис. Аналогично строятся гипорболические параболоиды с осью Oх (рис. 46 -47) и осью Оу (рис. 48 -49). Рис. 46. Гиперболический параболоид с осью Oх (по оси Оу)

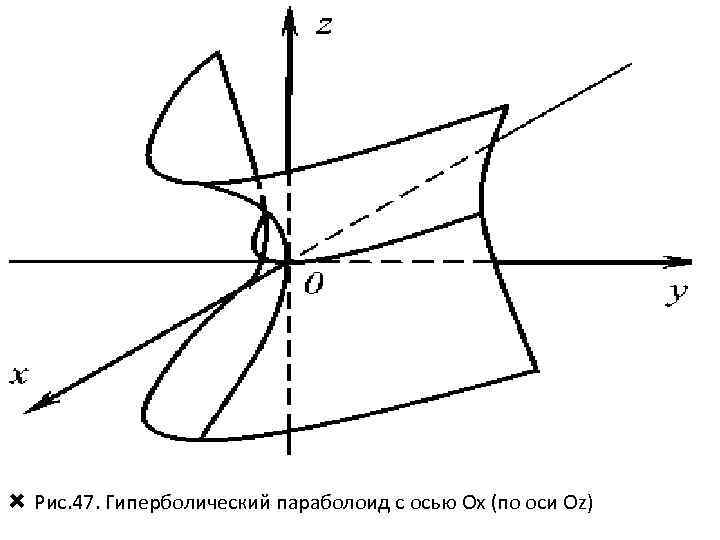Рис. 47. Гиперболический параболоид с осью Oх (по оси Оz) Рис. 47. Гиперболический параболоид с осью Oх (по оси Оz)

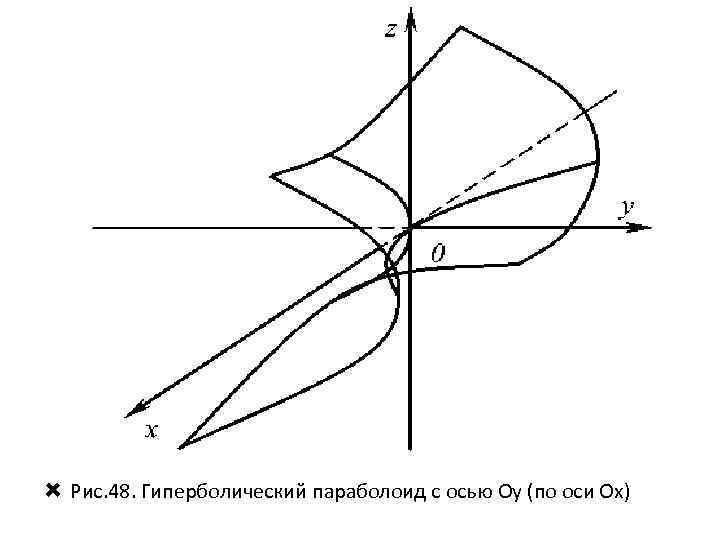Рис. 48. Гиперболический параболоид с осью Oу (по оси Ох) Рис. 48. Гиперболический параболоид с осью Oу (по оси Ох)

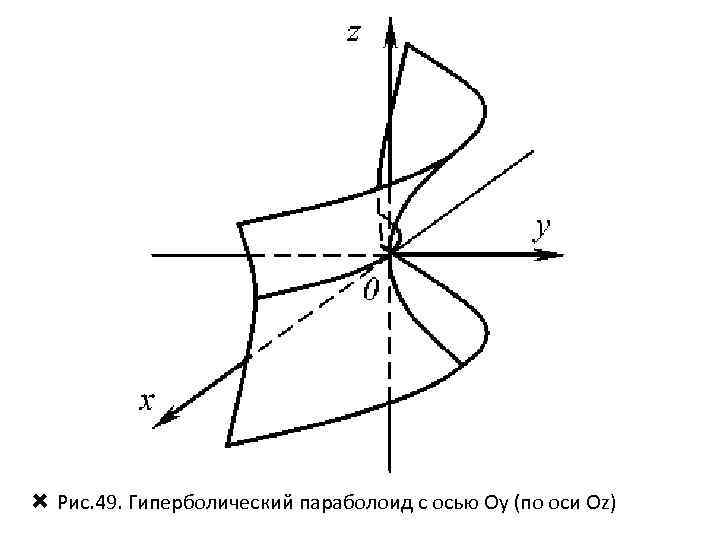Рис. 49. Гиперболический параболоид с осью Oу (по оси Оz) Рис. 49. Гиперболический параболоид с осью Oу (по оси Оz)

Образцы решения задач Пример. Выясним, какую поверхность в пространстве описывает уравнение x = y Образцы решения задач Пример. Выясним, какую поверхность в пространстве описывает уравнение x = y 2 + z 2. Решение. Используя метод сечений, получим: В сечении плоскостями x = h, параллельными плоскости YOZ: y 2 + z 2 = h x = h Видно, что при h>0 в сечении получаются окружности с центрами на оси OX радиуса h, т. е. при возрастании h радиусы окружностей неограниченно возрастают. При h = 0 плоскость x = 0 касается поверхности в начале координат (0, 0, 0) и, наконец, при h<0 плоскость x = h не пересекает поверхности (в сечении — пустое множество).

Аналогично исследуются сечения плоскостями, параллельными координатным плоскостям XOZ и XOY. В частности, x Аналогично исследуются сечения плоскостями, параллельными координатным плоскостям XOZ и XOY. В частности, x = z 2 x = y 2 y = 0 z = 0 т. е. в сечении координатными плоскостями y = 0 и z = 0 получаются параболыс вершинами в начале координат, ветви которых направлены в положительном направлении оси OX. Ответ: параболоид вращения — поверхность, которую описывает парабола с вершиной в начале координат при вращении вокруг оси OX.

Конус и цилиндры второго порядка Конус второго порядка Убедимся, что вещественный конус S образован Конус и цилиндры второго порядка Конус второго порядка Убедимся, что вещественный конус S образован прямыми линиями, проходящими через начало О координат. Естественно называть точку О вершиной конуса. Для доказательства сформулированного утверждения, очевидно, достаточно установить, что прямая L, соединяющая произвольную, отличную от начала координат точку М 0(х0, у0, z 0) конуса (6) и начало координат О, целиком располагается на конусе, т. е. координаты (х, у, z) любой точки М прямой L удовлетворяют уравнению (6). (17)

Так как точка М 0(х0, у0, z 0) лежит на конусе (6), то: Так как точка М 0(х0, у0, z 0) лежит на конусе (6), то: Координаты (х, у, z) любой точки М прямой L равны соответственно tx 0 , ty 0 , tz 0 , где t—некоторое число. Подставляя эти значения для х, у и z в левую часть (6), вынося затем t 2 за скобку и учитывая (17), мы убедимся в том, что М лежит на конусе. Таким образом, утверждение доказано. Представление о форме конуса может быть получено методом сечений. Легко убедиться, что сечения конуса плоскостями z = h представляют собой эллипсы с полуосями. Рассмотрим построение конических поверхностей с разными осями, предварительно исследовав их методом сечений.

– конус второго порядка с осью Oz. Плоскость Oxy: в сечении получаем пару – конус второго порядка с осью Oz. Плоскость Oxy: в сечении получаем пару мнимых пересекающихся прямых. При z = h (h 0) в каждом сечении будет эллипс. Плоскость Oxz: в сечении получаем пару пересекающихся прямых. Плоскость Oyz: в сечении получаем пару пересекающихся прямых. Построим поверхность, последовательно изображая полученные в сечениях прямые и эллипсы.

• Начнем построение с изображения пересекающихся прямых в плоскости Oxz. Выберем произвольную высоту • Начнем построение с изображения пересекающихся прямых в плоскости Oxz. Выберем произвольную высоту конуса h, проведем прямые параллельные оси Оx, получим плоскость, образованную данными прямыми (рис. 50).

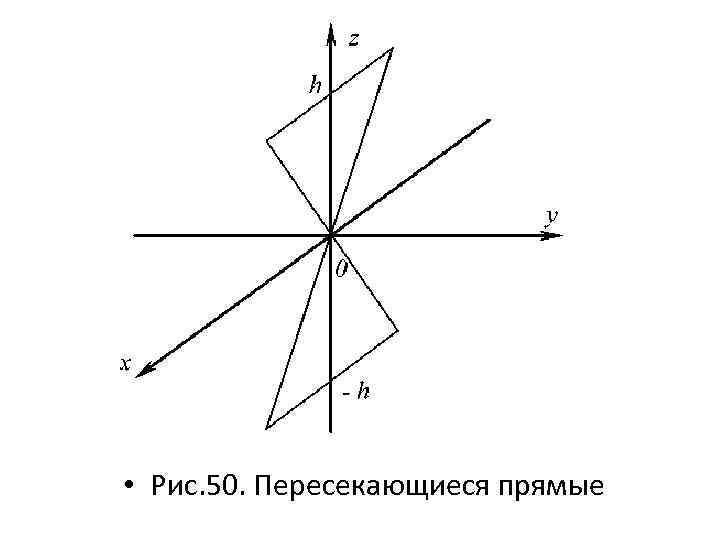• Рис. 50. Пересекающиеся прямые • Рис. 50. Пересекающиеся прямые

• Построим пересекающиеся прямые в плоскости Oyz. Через высоту конуса h, проведем прямые • Построим пересекающиеся прямые в плоскости Oyz. Через высоту конуса h, проведем прямые параллельные оси Оy, получим плоскость, образованную данными прямыми (рис. 51).

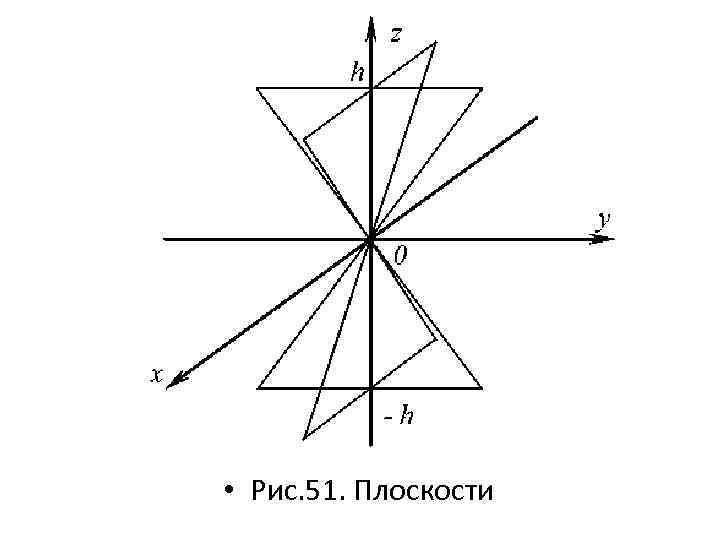• Рис. 51. Плоскости • Рис. 51. Плоскости

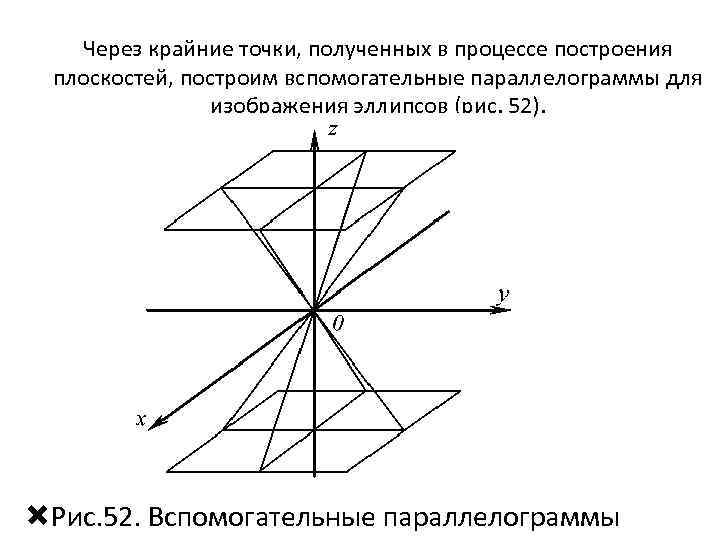Через крайние точки, полученных в процессе построения плоскостей, построим вспомогательные параллелограммы для изображения эллипсов Через крайние точки, полученных в процессе построения плоскостей, построим вспомогательные параллелограммы для изображения эллипсов (рис. 52). Рис. 52. Вспомогательные параллелограммы

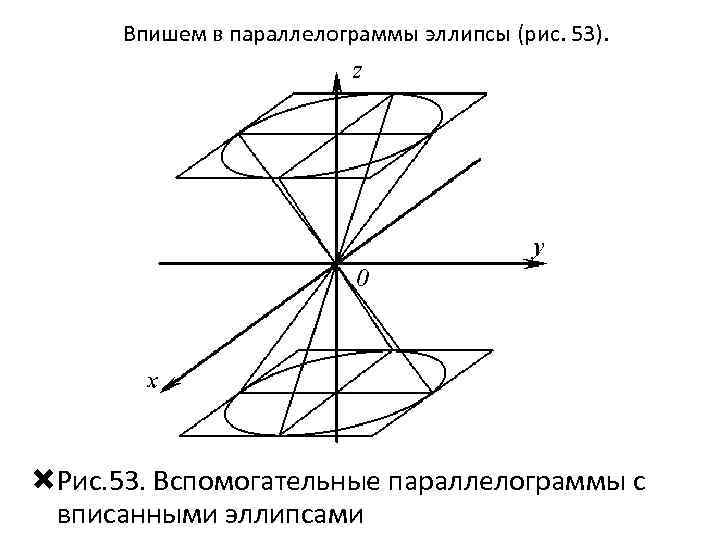Впишем в параллелограммы эллипсы (рис. 53). Рис. 53. Вспомогательные параллелограммы с вписанными эллипсами Впишем в параллелограммы эллипсы (рис. 53). Рис. 53. Вспомогательные параллелограммы с вписанными эллипсами

• Получили изображение всех трех сечений. Уберем вспомогательные параллелограммы, покажем видимые и невидимые • Получили изображение всех трех сечений. Уберем вспомогательные параллелограммы, покажем видимые и невидимые элементы конической поверхности, проведем очерковую линию (рис. 54).

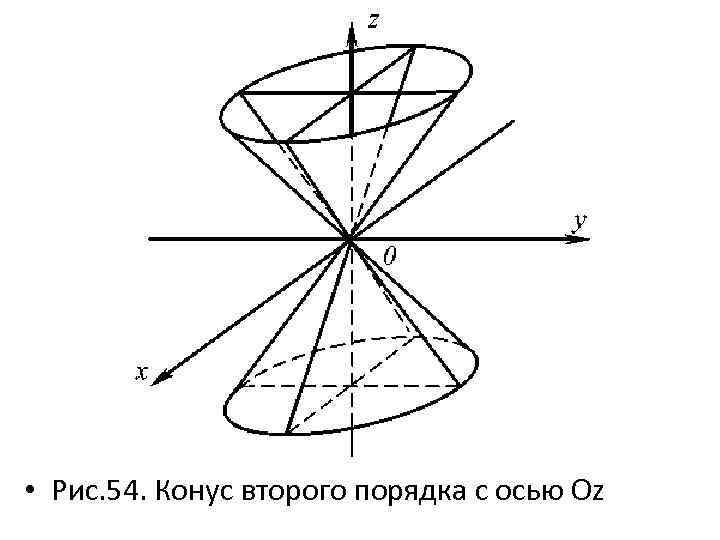• Рис. 54. Конус второго порядка с осью Oz • Рис. 54. Конус второго порядка с осью Oz

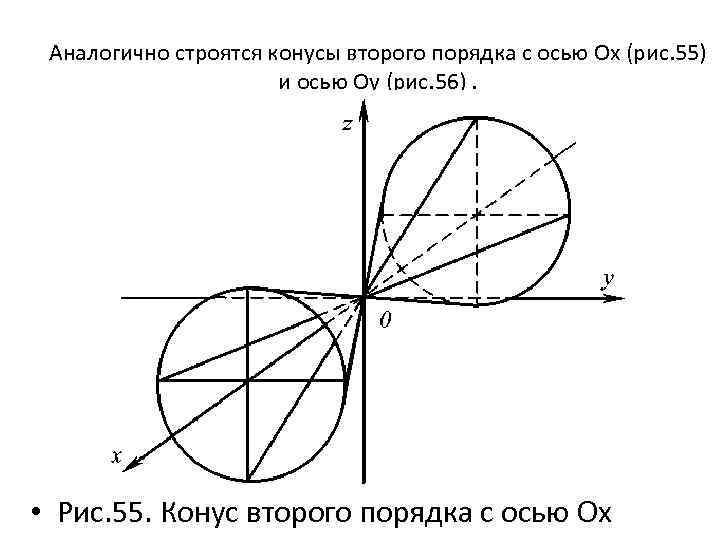Аналогично строятся конусы второго порядка с осью Oх (рис. 55) и осью Оу (рис. Аналогично строятся конусы второго порядка с осью Oх (рис. 55) и осью Оу (рис. 56). • Рис. 55. Конус второго порядка с осью Oх

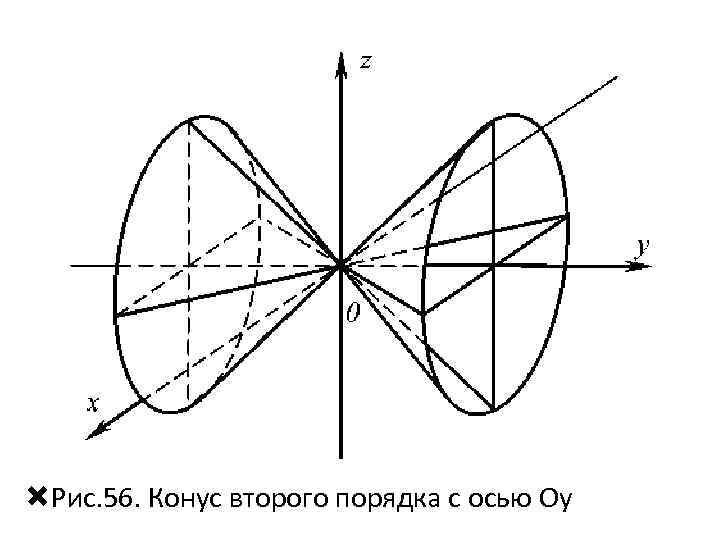Рис. 56. Конус второго порядка с осью Oу Рис. 56. Конус второго порядка с осью Oу

• Эллиптический цилиндр • (18) • (18) - эллиптический цилиндр с осью Оz. • Эллиптический цилиндр • (18) • (18) - эллиптический цилиндр с осью Оz. Построение данного цилиндра начинаем с изображения эллипса с полуосями: а и b. Предварительно строим параллелограмм, в который впишем эллипс (рис. 57).

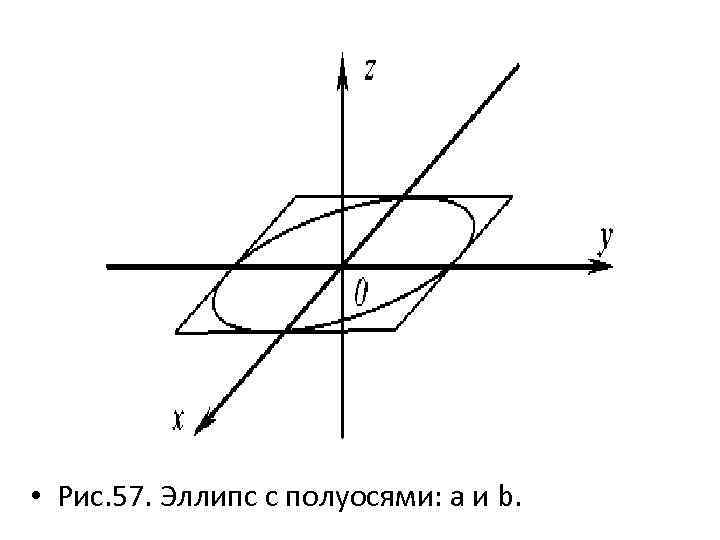• Рис. 57. Эллипс с полуосями: а и b. • Рис. 57. Эллипс с полуосями: а и b.

Выбираем произвольно высоту h цилиндра и перемещаем эллипс относительно оси Оz. Для удобства Выбираем произвольно высоту h цилиндра и перемещаем эллипс относительно оси Оz. Для удобства изображения строим вспомогательную систему координат с центом в точке с координатами (0; 0; h) (рис. 58). Замечание. Для компактности чертежей, как на данном примере, так и далее будим осуществлять построение в положительном направлении соответствующей оси.

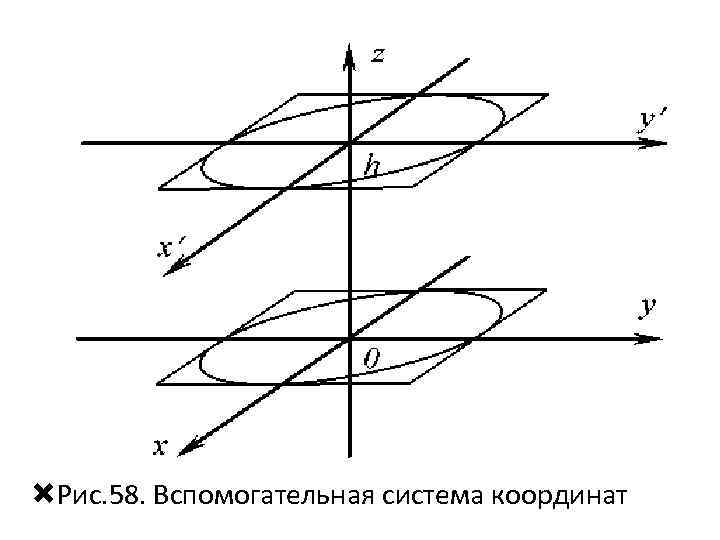Рис. 58. Вспомогательная система координат Рис. 58. Вспомогательная система координат

• Соединяем соответствующие точки поверхности, убираем вспомогательные линии, проводим очерковую линию и показываем • Соединяем соответствующие точки поверхности, убираем вспомогательные линии, проводим очерковую линию и показываем видимые и невидимые элементы эллиптического цилиндра (рис. 59).

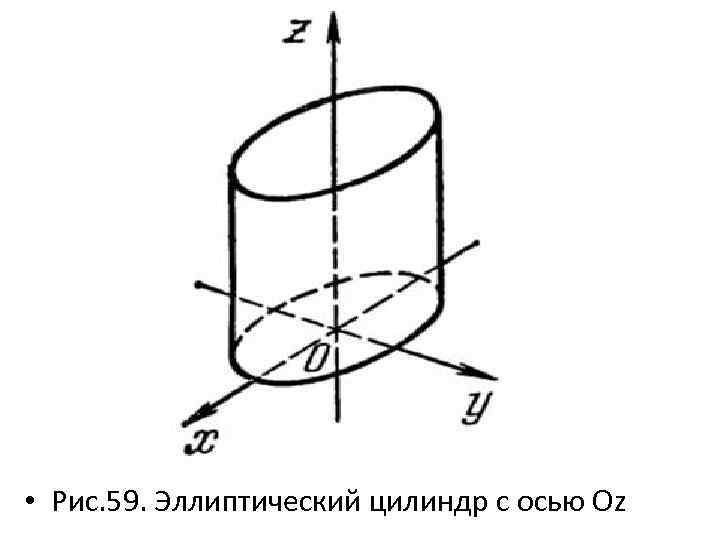• Рис. 59. Эллиптический цилиндр с осью Оz • Рис. 59. Эллиптический цилиндр с осью Оz

• По приведенной схеме осуществляется построение цилиндров данного вида: • – с осью • По приведенной схеме осуществляется построение цилиндров данного вида: • – с осью Ox (рис. 60) и • – с осью Oy (рис. 61).

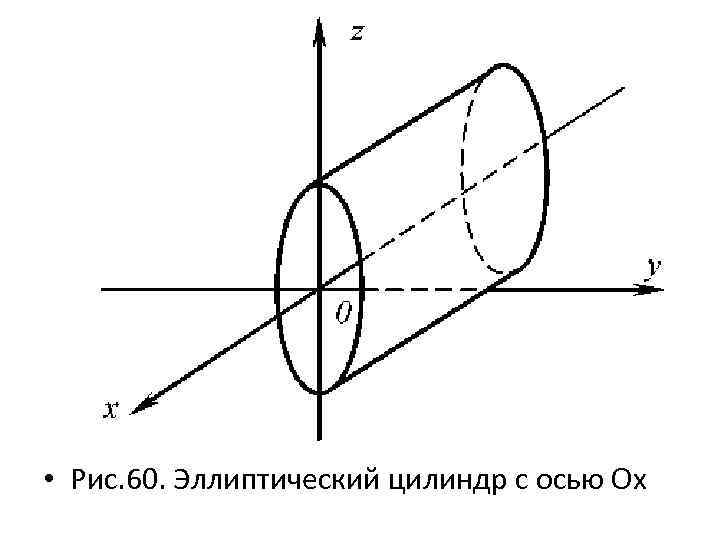• Рис. 60. Эллиптический цилиндр с осью Ox • Рис. 60. Эллиптический цилиндр с осью Ox

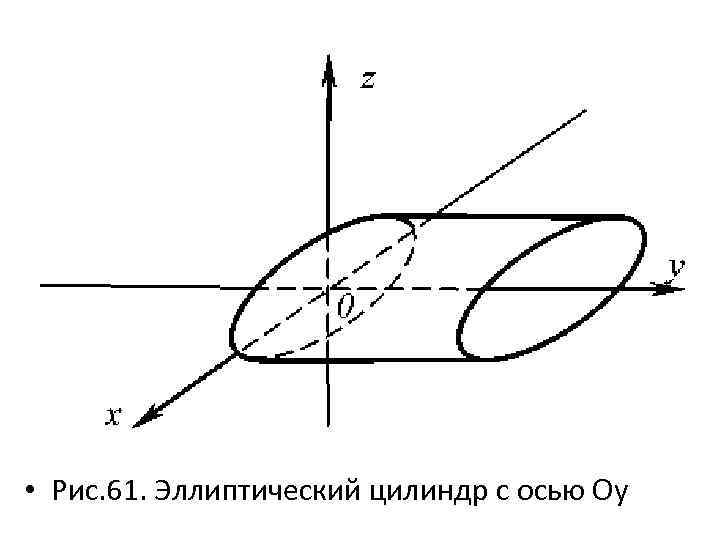• Рис. 61. Эллиптический цилиндр с осью Oy • Рис. 61. Эллиптический цилиндр с осью Oy

• • • Гиперболический цилиндр – гиперболический цилиндр с осью Оz. Построение данного • • • Гиперболический цилиндр – гиперболический цилиндр с осью Оz. Построение данного цилиндра начнем с построения гиперболы • где b – действительная полуось и a – мнимая полуось (рис. 62).

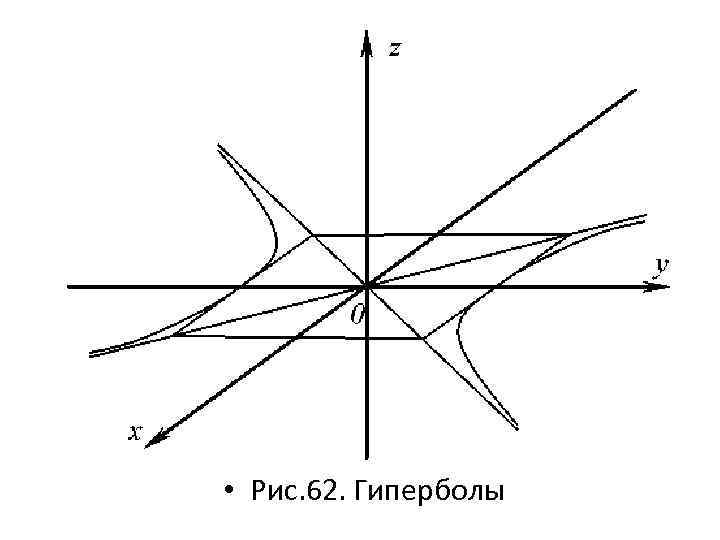• Рис. 62. Гиперболы • Рис. 62. Гиперболы

• Выбираем произвольно высоту h цилиндра и перемещаем гиперболу относительно оси Оz. Для • Выбираем произвольно высоту h цилиндра и перемещаем гиперболу относительно оси Оz. Для удобства изображения строим вспомогательную систему координат с центом в точке с координатами (0; 0; h) (рис. 63).

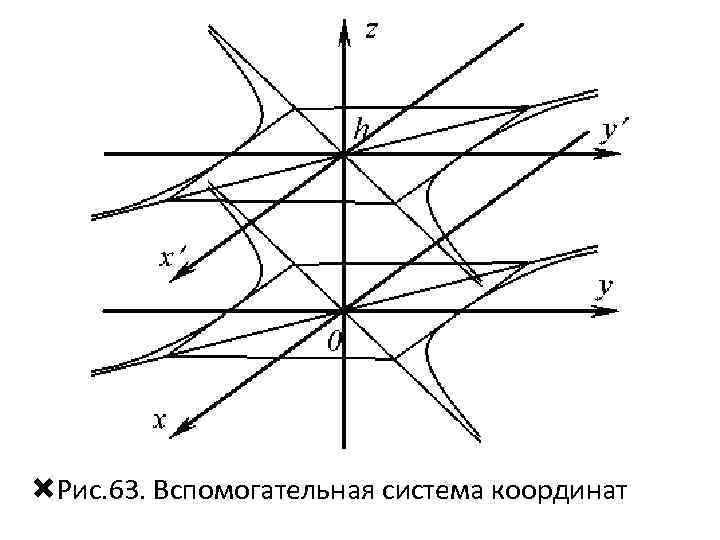Рис. 63. Вспомогательная система координат Рис. 63. Вспомогательная система координат

• Соединяем соответствующие точки, убираем вспомогательные линии, проводим очерковые линии и показываем видимые • Соединяем соответствующие точки, убираем вспомогательные линии, проводим очерковые линии и показываем видимые и невидимые элементы гиперболического цилиндра (рис. 64).

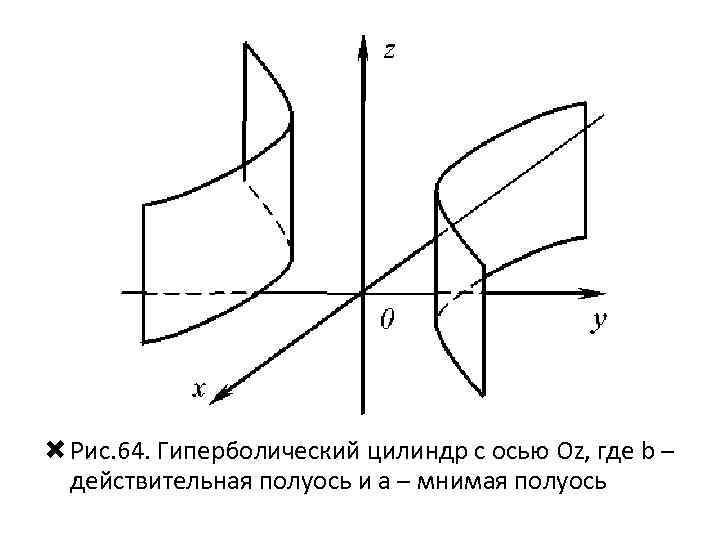Рис. 64. Гиперболический цилиндр с осью Оz, где b – действительная полуось и Рис. 64. Гиперболический цилиндр с осью Оz, где b – действительная полуось и a – мнимая полуось

• По приведенной схеме осуществляется построение следующих видов гиперболических цилиндров: • – с • По приведенной схеме осуществляется построение следующих видов гиперболических цилиндров: • – с осью Oz, • где a – действительная и b – • мнимая полуоси (рис. 65)

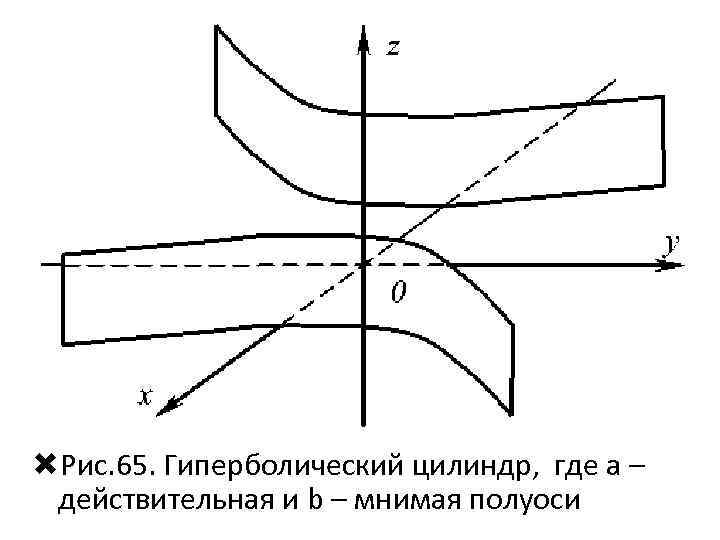Рис. 65. Гиперболический цилиндр, где a – действительная и b – мнимая полуоси Рис. 65. Гиперболический цилиндр, где a – действительная и b – мнимая полуоси

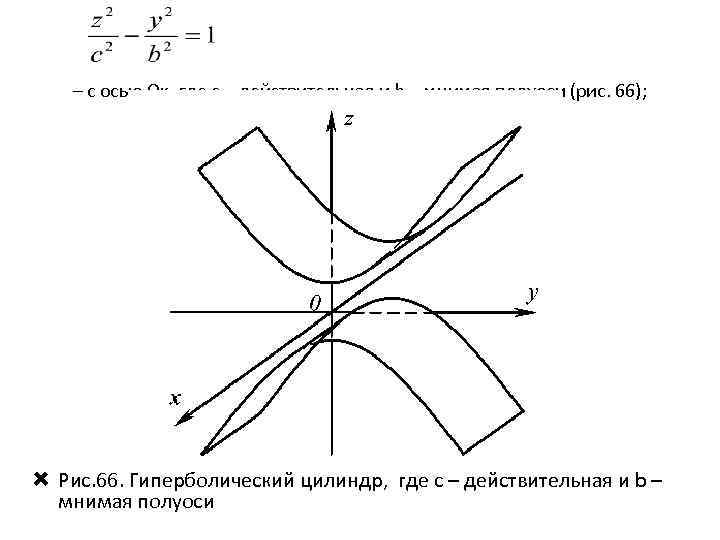– с осью Ox, где с – действительная и b – мнимая полуоси (рис. – с осью Ox, где с – действительная и b – мнимая полуоси (рис. 66); Рис. 66. Гиперболический цилиндр, где с – действительная и b – мнимая полуоси

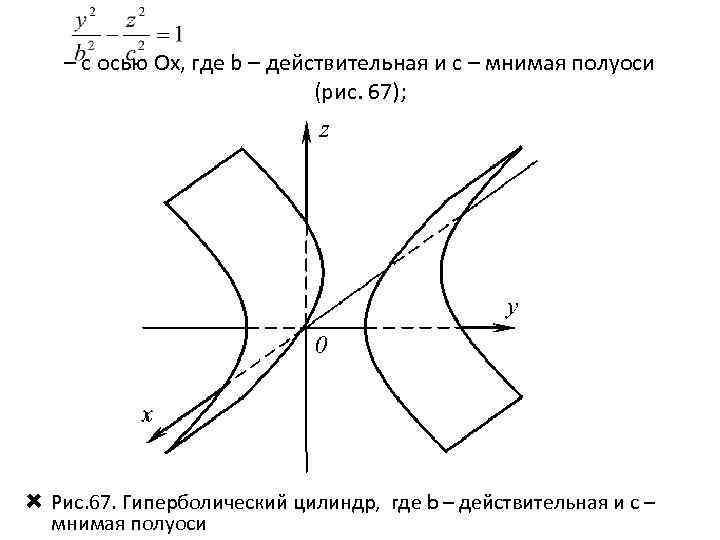– с осью Ox, где b – действительная и с – мнимая полуоси (рис. – с осью Ox, где b – действительная и с – мнимая полуоси (рис. 67); Рис. 67. Гиперболический цилиндр, где b – действительная и с – мнимая полуоси

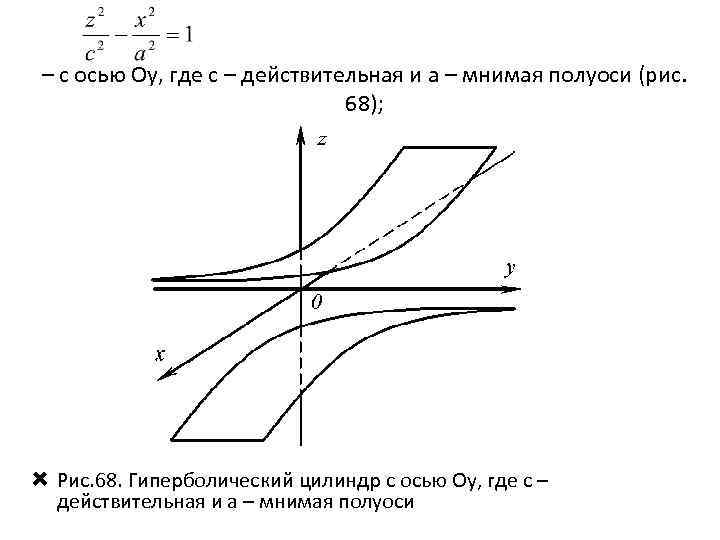– с осью Oy, где с – действительная и a – мнимая полуоси (рис. – с осью Oy, где с – действительная и a – мнимая полуоси (рис. 68); Рис. 68. Гиперболический цилиндр с осью Oy, где с – действительная и a – мнимая полуоси

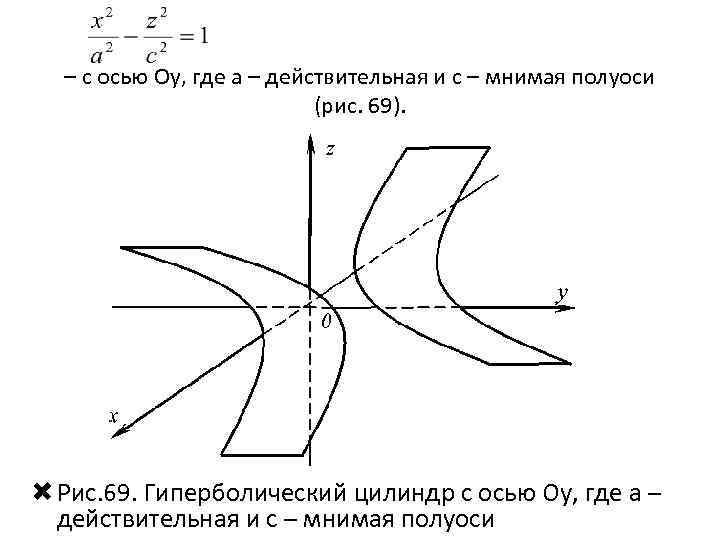– с осью Oy, где a – действительная и с – мнимая полуоси (рис. – с осью Oy, где a – действительная и с – мнимая полуоси (рис. 69). Рис. 69. Гиперболический цилиндр с осью Oy, где a – действительная и с – мнимая полуоси

• • • Параболический цилиндр a 33 z 2 + 2 q´y = • • • Параболический цилиндр a 33 z 2 + 2 q´y = 0 (19) - параболический цилиндр с осью Оz Построение данного цилиндра начнем с построения параболы, предварительно составив таблицу значений для переменных х и у (рис. 70).

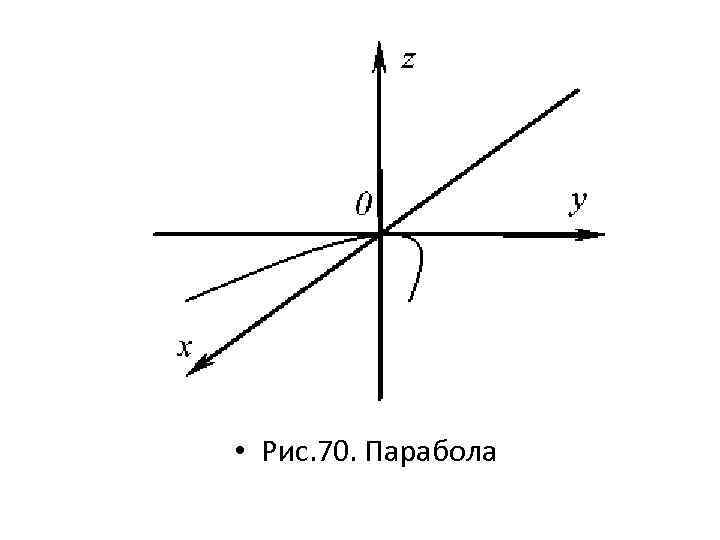• Рис. 70. Парабола • Рис. 70. Парабола

• Выбираем произвольно высоту h цилиндра и перемещаем параболу относительно оси Оz. Для • Выбираем произвольно высоту h цилиндра и перемещаем параболу относительно оси Оz. Для удобства изображения строим вспомогательную систему координат с центом в точке с координатами (0; 0; h) (рис. 71).

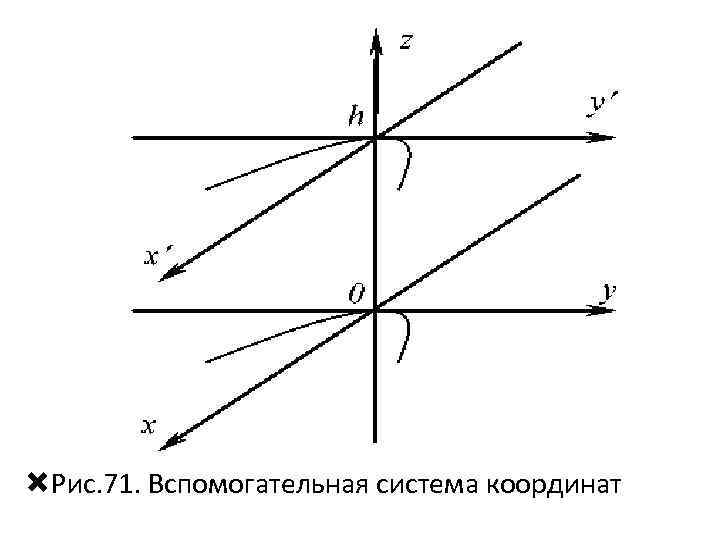Рис. 71. Вспомогательная система координат Рис. 71. Вспомогательная система координат

• Соединяем соответствующие точки, убираем вспомогательные линии, проводим очерковые линии и показываем видимые • Соединяем соответствующие точки, убираем вспомогательные линии, проводим очерковые линии и показываем видимые и невидимые элементы параболического цилиндра (рис. 72).

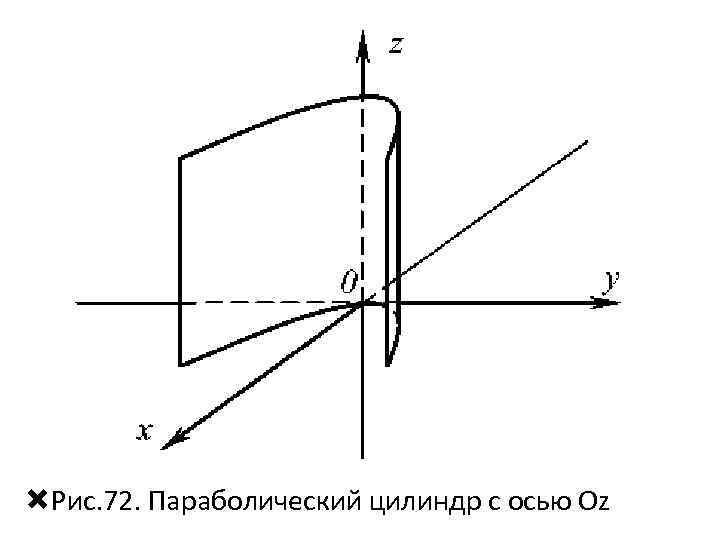Рис. 72. Параболический цилиндр с осью Оz Рис. 72. Параболический цилиндр с осью Оz

• По приведенной схеме осуществляется построение следующих видов параболических цилиндров: • По приведенной схеме осуществляется построение следующих видов параболических цилиндров:

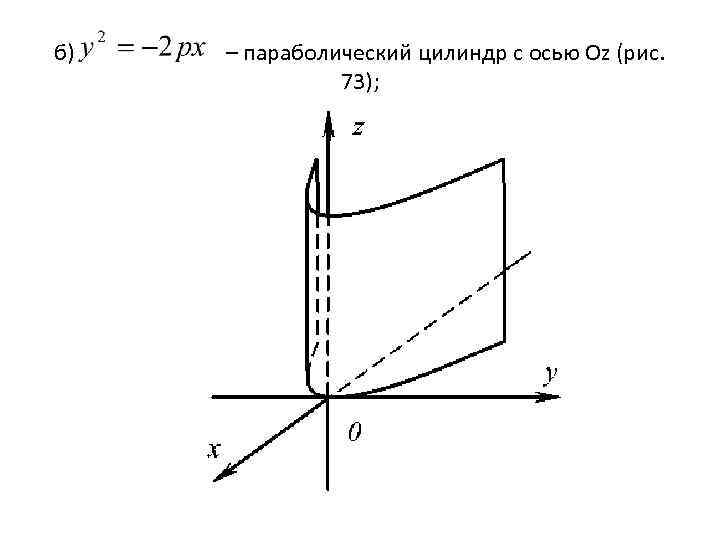б) – параболический цилиндр с осью Оz (рис. 73); б) – параболический цилиндр с осью Оz (рис. 73);

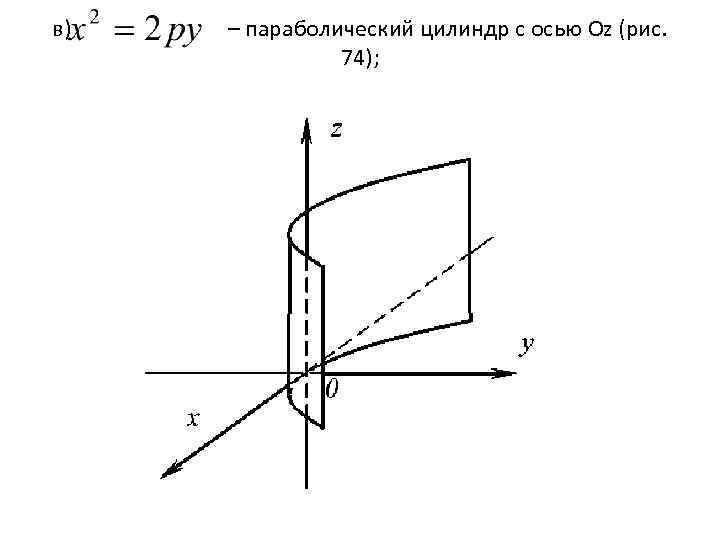в) – параболический цилиндр с осью Оz (рис. 74); в) – параболический цилиндр с осью Оz (рис. 74);

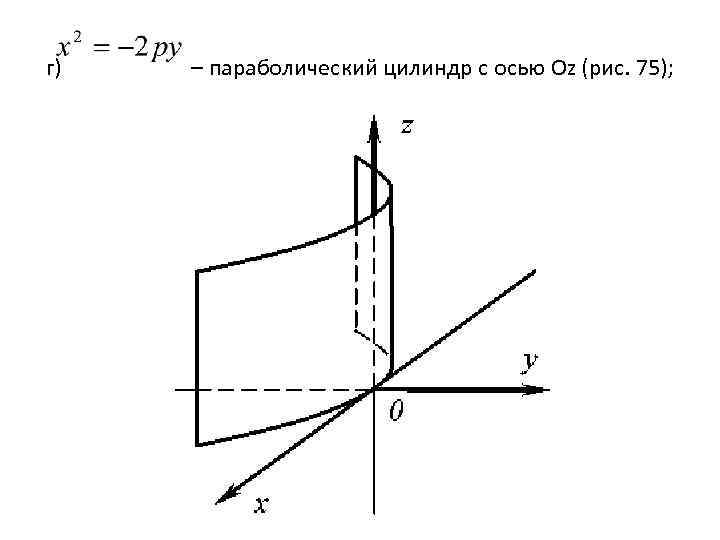г) – параболический цилиндр с осью Оz (рис. 75); г) – параболический цилиндр с осью Оz (рис. 75);

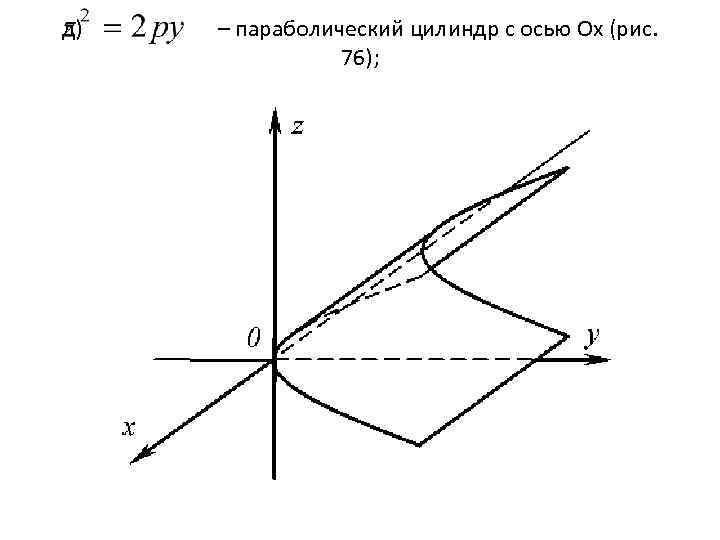д) – параболический цилиндр с осью Оx (рис. 76); д) – параболический цилиндр с осью Оx (рис. 76);

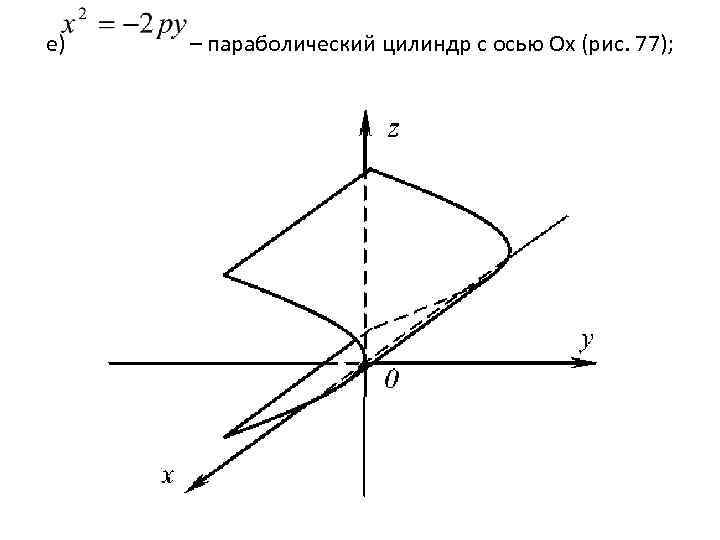е) – параболический цилиндр с осью Оx (рис. 77); е) – параболический цилиндр с осью Оx (рис. 77);

ж) – параболический цилиндр с осью Оx (рис. 78); ж) – параболический цилиндр с осью Оx (рис. 78);

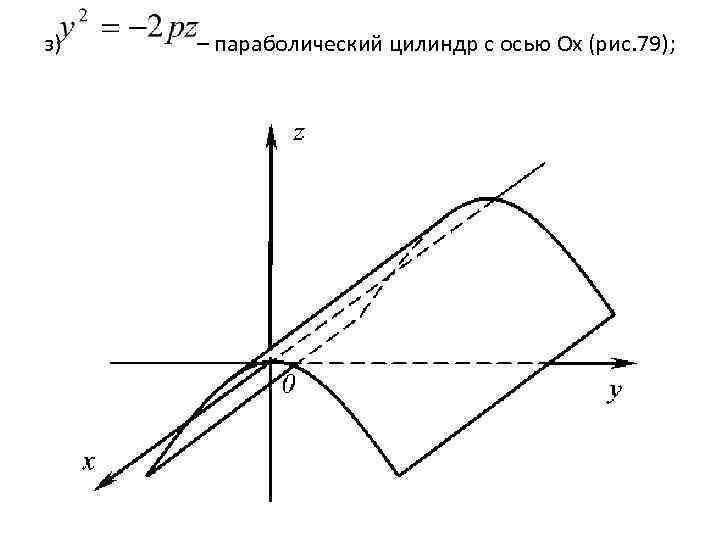з) – параболический цилиндр с осью Оx (рис. 79); з) – параболический цилиндр с осью Оx (рис. 79);

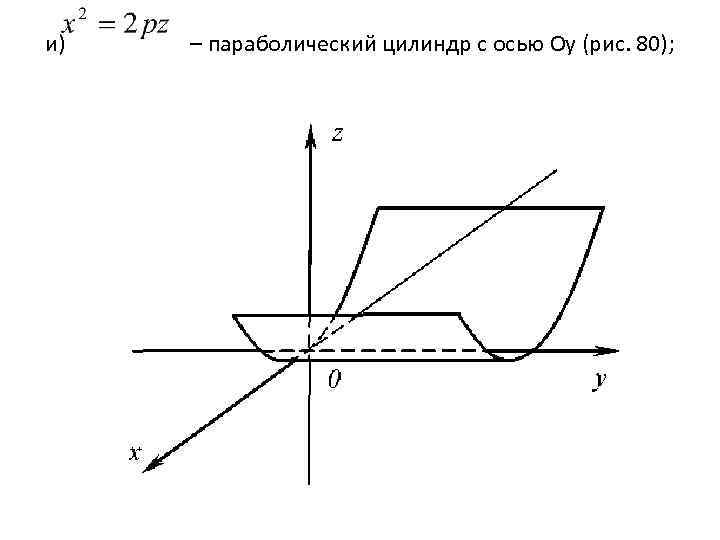и) – параболический цилиндр с осью Оy (рис. 80); и) – параболический цилиндр с осью Оy (рис. 80);

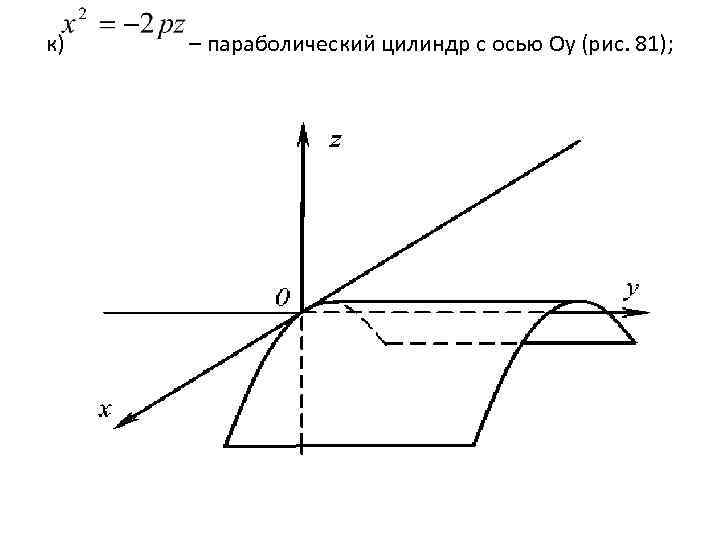к) – параболический цилиндр с осью Оy (рис. 81); к) – параболический цилиндр с осью Оy (рис. 81);

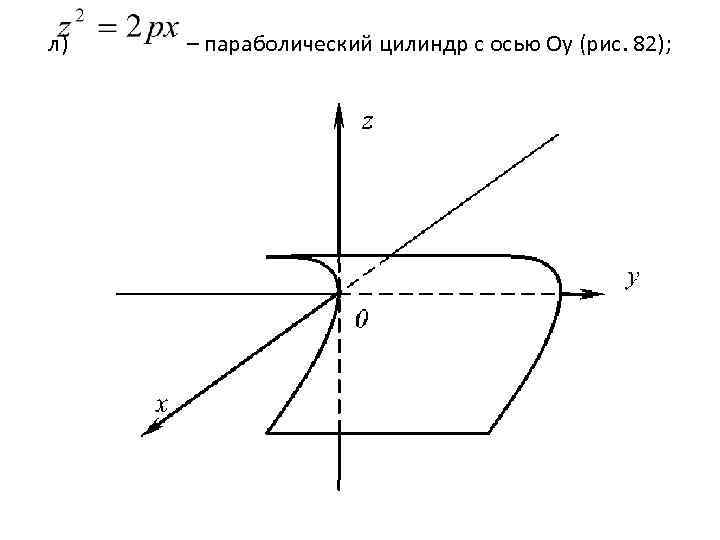л) – параболический цилиндр с осью Оy (рис. 82); л) – параболический цилиндр с осью Оy (рис. 82);

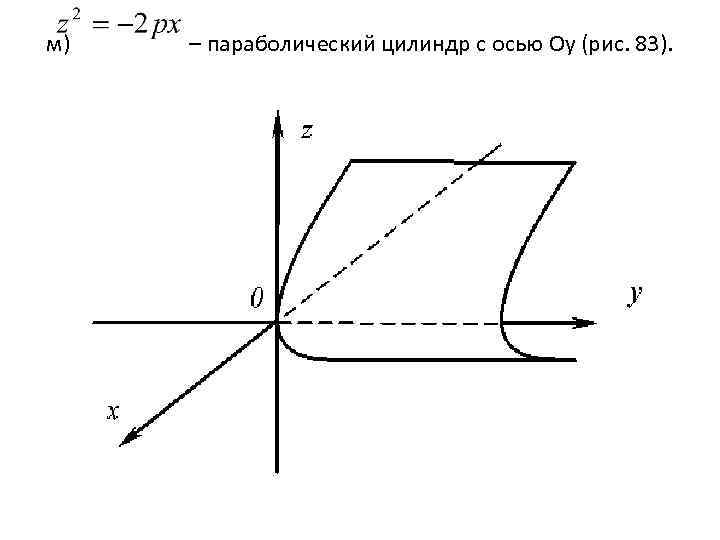м) – параболический цилиндр с осью Оy (рис. 83). м) – параболический цилиндр с осью Оy (рис. 83).

Образцы решения задач Пример 1. Выясним, какую поверхность в пространстве описывает уравнение x 2 Образцы решения задач Пример 1. Выясним, какую поверхность в пространстве описывает уравнение x 2 + z 2 + 2 z = 0. Решение. Выделяя полный квадрат, получим x 2 + (z + 1)2 = 1. Так как уравнение не содержит y , то оно описывает цилиндрическую поверхность с образующими, параллельными оси OY , а направляющей является окружность радиуса R = 1 с центром в точке (0, y, − 1). Ответ: круглый цилиндр с образующими, параллельными оси OY.

Пример 2. Выясним, какую поверхность в пространстве описывает уравнение x 2 − y Пример 2. Выясним, какую поверхность в пространстве описывает уравнение x 2 − y 2 + 2 y − 2 = 0. Решение. Выделяя полный квадрат, получим x 2 − (y − 1)2 = 1. Так как уравнение не содержит z , то оно описывает цилиндрическую поверхность с образующими, параллельными оси OZ , а направляющей является гипербола. Ответ: гиперболический цилиндр с образующими, параллельными оси OZ.

Пример 3. Выясним, какую поверхность в пространстве описывает уравнение x 2 + 2 Пример 3. Выясним, какую поверхность в пространстве описывает уравнение x 2 + 2 x + 2 y 2 − 4 z 2 = 1. Решение. Поскольку уравнение сдержит x 2 и x , необходимо выделить полный квадрат: (x + 1)2 + 2 y 2 − 4 z 2 = 0 и перейти к новой системе координат, полученной из исходной с помощью параллельного переноса так, что начало новой системы координат помещено в точку O'(− 1, 0, 0): x'2 + 2 y'2 − 4 z'2 = 0 , где x' = x + 1 , y' = y и z' = z. Получаем каноническое уравнение конуса с осью симметрии, параллельной оси OZ. Ответ: конус с центром в точке O'( − 1, 0, 0) и осью симметрии, параллельной оси OZ.

Пример 4. Выясним, какую поверхность в пространстве описывает уравнение Решение. Поскольку уравнение сдержит Пример 4. Выясним, какую поверхность в пространстве описывает уравнение Решение. Поскольку уравнение сдержит корень, необходимо возвести обе части уравнения в квадрат (при этом мы приобретаем "лишние" решения и, следовательно, "лишние" точки). Имеем: x 2 + z 2 − y 2 = 0. Используя метод сечений, легко убедиться, что это круглый конус с вершиной в начале координат, осью которого является ось OY. Ответ: половина круглого конуса (y ≥ 0) с вершиной в начале координат, осью которого является ось OY.