обратн функц.ppt
- Количество слайдов: 9

ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ. Обратная функция — функция, обращающая зависимость, выражаемую данной функцией.

Если функция у = f ( х ) принимает каждое своё значение у только при одном значении х, то эту функцию называют обратимой.

Пусть у = f(x) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определённое число х из области её определения, такое, что f(x) = y. Это соответствие определяет функцию х от у, которую обозначим х = g(y). Поменяем местами х и у: у = g(x). Функцию у = g(x) называют обратной к функции у = f(x)

Не для всякой функции можно указать обратную. Условие обратимости функции - ее монотонность, то есть функция должна только возрастать или только убывать. Если функция не монотонна на всей области определения, но монотонная на некотором промежутке, тогда можно задать обратную ей функцию только на этом промежутке.

ПРИВЕДЕМ ПРИМЕР.
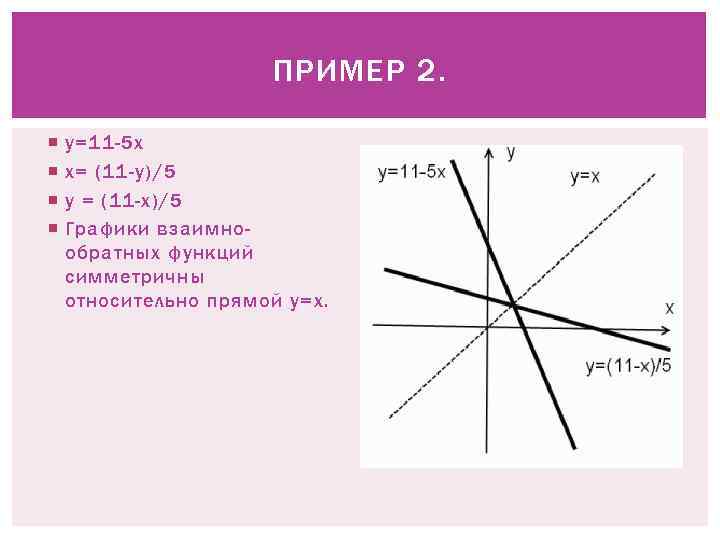
ПРИМЕР 2. y=11 -5 x x= (11 -y)/5 y = (11 -x)/5 Графики взаимнообратных функций симметричны относительно прямой y=x.

ПРИМЕР 3. Дана функция: Найдем обратную ей функцию. 1. Выразим x 2. Поменяем x и y местами.
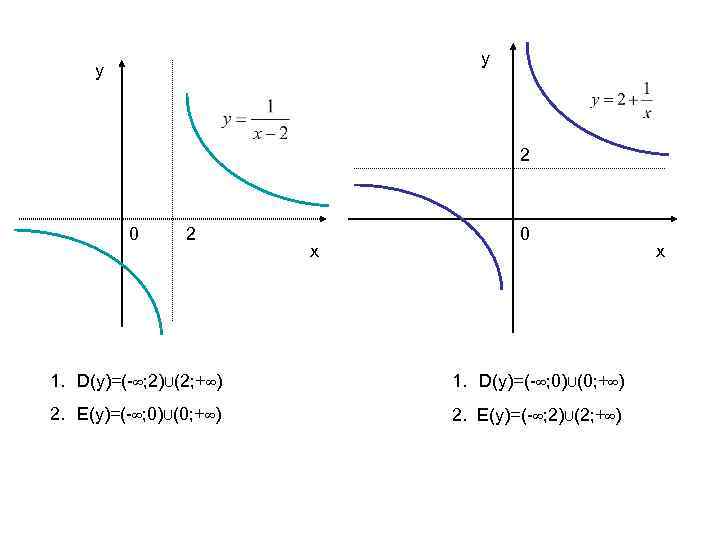
у у 2 0 2 х 0 1. D(у)=(-∞; 2)∪(2; +∞) 1. D(у)=(-∞; 0)∪(0; +∞) 2. Е(у)=(-∞; 2)∪(2; +∞) х

Свойства обратных функций • 1. Область определения обратной функции f(-х) совпадает с множеством значений исходной f(х), а множество значений обратной функции f(-х)с овпадает с областью определения исходной функции f(х): • D(f(-x)) = E(f(x)), E(f(-x)) = D(f(-x)). • 2. Монотонная функция является обратимой: • если функция f(x) возрастает, то обратная к ней функция f(-x) также возрастает; • если функция f(x) убывает, то обратная к ней функция f(-x) также убывает.
обратн функц.ppt