Понятие моделирования










 Понятие моделирования Способы представления моделей Модель — способ замещения реального объекта, используемый для его изучения. Модель вместо исходного объекта используется в случаях, когда эксперимент опасен, дорог, происходит в неудобном масштабе пространства и времени (долговременен, слишком кратковременен, протяжен…), невозможен, неповторим, ненагляден и т. д. Моделирование — это построение, совершенствование, изучение и применение моделей реально существующих или проектируемых объектов (процессов и явлений).
Понятие моделирования Способы представления моделей Модель — способ замещения реального объекта, используемый для его изучения. Модель вместо исходного объекта используется в случаях, когда эксперимент опасен, дорог, происходит в неудобном масштабе пространства и времени (долговременен, слишком кратковременен, протяжен…), невозможен, неповторим, ненагляден и т. д. Моделирование — это построение, совершенствование, изучение и применение моделей реально существующих или проектируемых объектов (процессов и явлений).
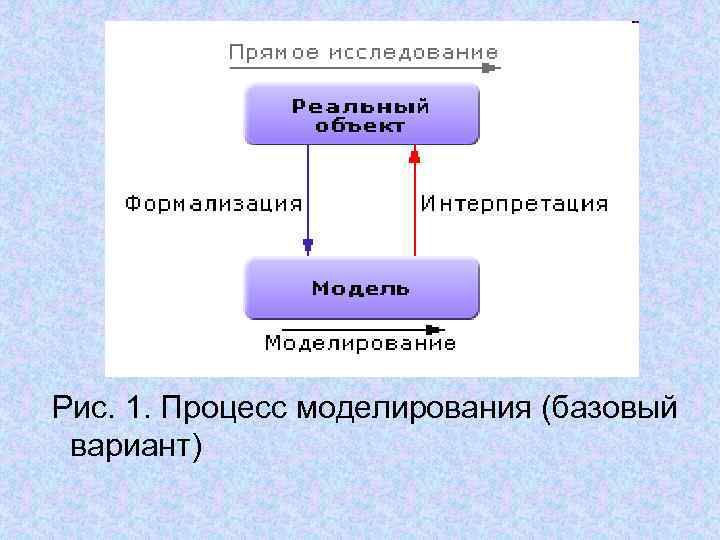
 Процесс моделирования есть процесс перехода из реальной области в виртуальную (модельную) посредством формализации, далее происходит изучение модели (собственно моделирование) и, наконец, интерпретация результатов как обратный переход из виртуальной области в реальную. Этот путь заменяет прямое исследование объекта в реальной области, то есть лобовое или интуитивное решение задачи. Итак, в самом простом случае технология моделирования подразумевает 3 этапа: формализация, собственно моделирование, интерпретация (рис. 1. ).
Процесс моделирования есть процесс перехода из реальной области в виртуальную (модельную) посредством формализации, далее происходит изучение модели (собственно моделирование) и, наконец, интерпретация результатов как обратный переход из виртуальной области в реальную. Этот путь заменяет прямое исследование объекта в реальной области, то есть лобовое или интуитивное решение задачи. Итак, в самом простом случае технология моделирования подразумевает 3 этапа: формализация, собственно моделирование, интерпретация (рис. 1. ).
 Рис. 1. Процесс моделирования (базовый вариант)
Рис. 1. Процесс моделирования (базовый вариант)
 Компьютерная графика помогает организовать удобный естественный интерфейс для управления моделью, для наблюдения за её реакциями. Важно понимать, что пользователь взаимодействует с моделью не напрямую, а именно через интерфейс: с одной стороны он посылает ей исходные (входные) данные (например, с помощью окон ввода, кнопок, движков, командной строки и т. д. ), с другой — смотрит на результат работы модели, то есть воспринимает посредством интерфейса выходные данные. Искусственный интеллект подразумевает построение высших моделей (например, адаптивных, которые умеют самонастраиваться, умеют создавать друга и т. д. ). Подразумевается, что модель интеллекта в состоянии сама строить модели прикладных объектов и систем.
Компьютерная графика помогает организовать удобный естественный интерфейс для управления моделью, для наблюдения за её реакциями. Важно понимать, что пользователь взаимодействует с моделью не напрямую, а именно через интерфейс: с одной стороны он посылает ей исходные (входные) данные (например, с помощью окон ввода, кнопок, движков, командной строки и т. д. ), с другой — смотрит на результат работы модели, то есть воспринимает посредством интерфейса выходные данные. Искусственный интеллект подразумевает построение высших моделей (например, адаптивных, которые умеют самонастраиваться, умеют создавать друга и т. д. ). Подразумевается, что модель интеллекта в состоянии сама строить модели прикладных объектов и систем.
 Существуют всевозможные виды моделирования. Представлены некоторые из них: • Моделирование систем с распределенными параметрами при перемещении материальных масс; • Моделирование случайного события; • Моделирование полной группы несовместных событий; • Моделирование случайной величины с заданным законом распределения; • Моделирование нормально распределенных случайных величин • Моделирование системы случайных величин; • Моделирование систем массового обслуживания; • Моделирование производственных процессов и систем; • Моделирование марковских случайных процессов. Рассмотрим моделирование полной группы несовместных событий и моделирование производственных процессов и систем
Существуют всевозможные виды моделирования. Представлены некоторые из них: • Моделирование систем с распределенными параметрами при перемещении материальных масс; • Моделирование случайного события; • Моделирование полной группы несовместных событий; • Моделирование случайной величины с заданным законом распределения; • Моделирование нормально распределенных случайных величин • Моделирование системы случайных величин; • Моделирование систем массового обслуживания; • Моделирование производственных процессов и систем; • Моделирование марковских случайных процессов. Рассмотрим моделирование полной группы несовместных событий и моделирование производственных процессов и систем
 Моделирование полной группы несовместных событий События называются несовместными, если вероятность появления этих событий одновременно равна 0. Отсюда следует, что суммарная вероятность группы несовместных событий равна 1. Обозначим через a 1, a 2, …, an события, а через P 1, P 2, …, Pn — вероятности появления отдельных событий. Так как события несовместны, то сумма вероятностей их выпадения равна 1: P 1 + P 2 + … + Pn = 1.
Моделирование полной группы несовместных событий События называются несовместными, если вероятность появления этих событий одновременно равна 0. Отсюда следует, что суммарная вероятность группы несовместных событий равна 1. Обозначим через a 1, a 2, …, an события, а через P 1, P 2, …, Pn — вероятности появления отдельных событий. Так как события несовместны, то сумма вероятностей их выпадения равна 1: P 1 + P 2 + … + Pn = 1.
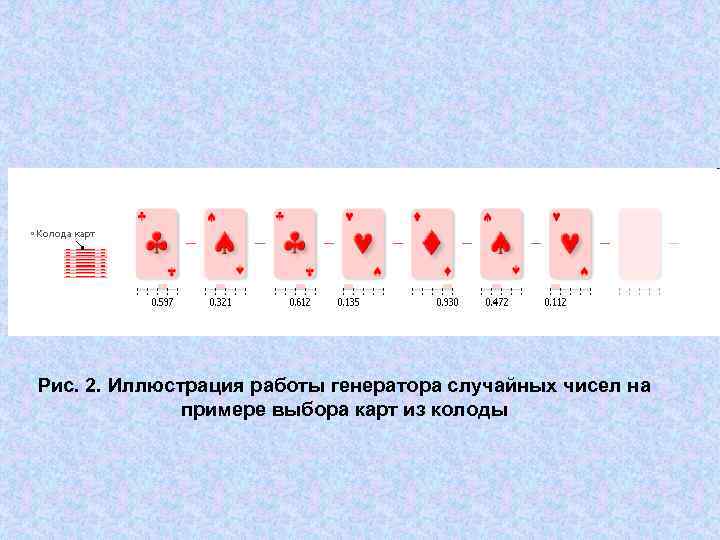
 Рис. 2. Иллюстрация работы генератора случайных чисел на примере выбора карт из колоды
Рис. 2. Иллюстрация работы генератора случайных чисел на примере выбора карт из колоды
 Пример с возможным исходом четырех несовместных случайных событий. Промоделируем выпадение последовательности событий — будем выбирать из колоды карт наугад карту (определять ее масть). Карты в колоду возвращать не будем. В колоде 36 карт четырех мастей по 9 карт каждой масти. Интервал от 0 до 1 разделим на равные четыре части: [0. 00— 0. 25], [0. 25— 0. 50], [0. 50— 0. 75], [0. 75— 1. 00]. Первая часть будет соответствовать картам масти червей (Ч), вторая — картам масти пик (П), третья — картам масти виней (В), четвертая — бубей (Б). Взять случайное равномерно распределенное число в интервале от 0 до 1 из таблицы случайных чисел. Пусть, например, это будет число 0. 597. Данное число попадает в третий интервал, соответствующий масти В. Произошло случайное событие: «Масть выпавшей карты — В» . Поскольку теперь в колоде 9 карт масти Ч, 9 карт масти П, 8 карт масти В, 9 карт масти Б, то интервал от 0 до 1 будет разбит на отрезки длиной: 9/35, 8/35, 9/35, то есть [0. 000— 0. 257], [0. 257— 0. 514], [0. 514— 0. 743], [0. 743— 1. 000]. Разыграем случайное равномерно распределенное число в интервале от 0 до 1. Например, 0. 321. Данное число попадает во второй интервал, соответствующий масти П. Продолжая процесс, можно получить (в зависимости от конкретных случайных чисел), например, такую последовательность: В—П—В—Ч—Б—П—Ч—… (в качестве иллюстрации см. рис. 2. ).
Пример с возможным исходом четырех несовместных случайных событий. Промоделируем выпадение последовательности событий — будем выбирать из колоды карт наугад карту (определять ее масть). Карты в колоду возвращать не будем. В колоде 36 карт четырех мастей по 9 карт каждой масти. Интервал от 0 до 1 разделим на равные четыре части: [0. 00— 0. 25], [0. 25— 0. 50], [0. 50— 0. 75], [0. 75— 1. 00]. Первая часть будет соответствовать картам масти червей (Ч), вторая — картам масти пик (П), третья — картам масти виней (В), четвертая — бубей (Б). Взять случайное равномерно распределенное число в интервале от 0 до 1 из таблицы случайных чисел. Пусть, например, это будет число 0. 597. Данное число попадает в третий интервал, соответствующий масти В. Произошло случайное событие: «Масть выпавшей карты — В» . Поскольку теперь в колоде 9 карт масти Ч, 9 карт масти П, 8 карт масти В, 9 карт масти Б, то интервал от 0 до 1 будет разбит на отрезки длиной: 9/35, 8/35, 9/35, то есть [0. 000— 0. 257], [0. 257— 0. 514], [0. 514— 0. 743], [0. 743— 1. 000]. Разыграем случайное равномерно распределенное число в интервале от 0 до 1. Например, 0. 321. Данное число попадает во второй интервал, соответствующий масти П. Продолжая процесс, можно получить (в зависимости от конкретных случайных чисел), например, такую последовательность: В—П—В—Ч—Б—П—Ч—… (в качестве иллюстрации см. рис. 2. ).
 Моделирование производственных процессов и систем Проектирование технологических процессов, проверка свойств проекта на модели, прогнозирование хода производства, настройка модели для производственных процессов, управление производством имеют ряд особенностей. Цель данного моделирования — обсудить возникающие при моделировании производственных процессов особенности. Допустим, что некоторый производственный процесс нелинеен. Это значит, что между входом X (то, чем управляем) и выходом Y (то, что наблюдаем) имеется нелинейная зависимость.
Моделирование производственных процессов и систем Проектирование технологических процессов, проверка свойств проекта на модели, прогнозирование хода производства, настройка модели для производственных процессов, управление производством имеют ряд особенностей. Цель данного моделирования — обсудить возникающие при моделировании производственных процессов особенности. Допустим, что некоторый производственный процесс нелинеен. Это значит, что между входом X (то, чем управляем) и выходом Y (то, что наблюдаем) имеется нелинейная зависимость.
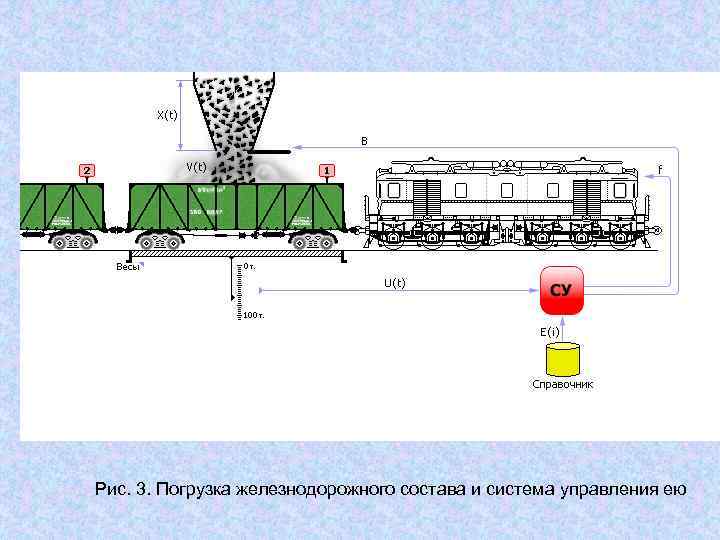
 Погрузка железнодорожного состава Рассмотрим процесс погрузки железнодорожного состава, состоящего из электровоза и прицепленных к нему трех вагонов (см. рис. 3. ). Над первым вагоном находится бункер, из которого насыпается груз. Вагон стоит на весах, измеряющих массу насыпанного груза. Грузоподъемность вагонов задана и известна системе управления из справочника в базе данных. Система управления (СУ) должна определить момент (и выдать управляющий сигнал электровозу), когда следует поставить под загрузку следующий вагон. После загрузки последнего вагона следует закрыть заслонку бункера.
Погрузка железнодорожного состава Рассмотрим процесс погрузки железнодорожного состава, состоящего из электровоза и прицепленных к нему трех вагонов (см. рис. 3. ). Над первым вагоном находится бункер, из которого насыпается груз. Вагон стоит на весах, измеряющих массу насыпанного груза. Грузоподъемность вагонов задана и известна системе управления из справочника в базе данных. Система управления (СУ) должна определить момент (и выдать управляющий сигнал электровозу), когда следует поставить под загрузку следующий вагон. После загрузки последнего вагона следует закрыть заслонку бункера.
 Рис. 3. Погрузка железнодорожного состава и система управления ею
Рис. 3. Погрузка железнодорожного состава и система управления ею
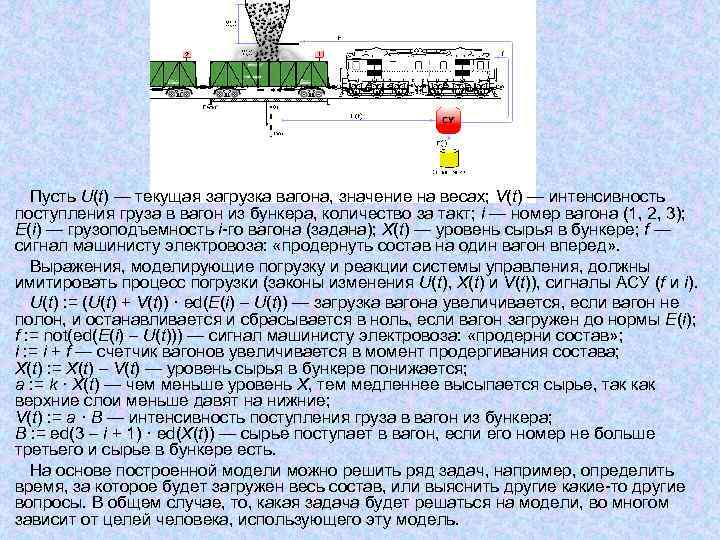
 Пусть U(t) — текущая загрузка вагона, значение на весах; V(t) — интенсивность поступления груза в вагон из бункера, количество за такт; i — номер вагона (1, 2, 3); E(i) — грузоподъемность i-го вагона (задана); X(t) — уровень сырья в бункере; f — сигнал машинисту электровоза: «продернуть состав на один вагон вперед» . Выражения, моделирующие погрузку и реакции системы управления, должны имитировать процесс погрузки (законы изменения U(t), X(t) и V(t)), сигналы АСУ (f и i). U(t) : = (U(t) + V(t)) · ed(E(i) – U(t)) — загрузка вагона увеличивается, если вагон не полон, и останавливается и сбрасывается в ноль, если вагон загружен до нормы E(i); f : = not(ed(E(i) – U(t))) — сигнал машинисту электровоза: «продерни состав» ; i : = i + f — счетчик вагонов увеличивается в момент продергивания состава; X(t) : = X(t) – V(t) — уровень сырья в бункере понижается; a : = k · X(t) — чем меньше уровень X, тем медленнее высыпается сырье, так как верхние слои меньше давят на нижние; V(t) : = a · B — интенсивность поступления груза в вагон из бункера; B : = ed(3 – i + 1) · ed(X(t)) — сырье поступает в вагон, если его номер не больше третьего и сырье в бункере есть. На основе построенной модели можно решить ряд задач, например, определить время, за которое будет загружен весь состав, или выяснить другие какие-то другие вопросы. В общем случае, то, какая задача будет решаться на модели, во многом зависит от целей человека, использующего эту модель.
Пусть U(t) — текущая загрузка вагона, значение на весах; V(t) — интенсивность поступления груза в вагон из бункера, количество за такт; i — номер вагона (1, 2, 3); E(i) — грузоподъемность i-го вагона (задана); X(t) — уровень сырья в бункере; f — сигнал машинисту электровоза: «продернуть состав на один вагон вперед» . Выражения, моделирующие погрузку и реакции системы управления, должны имитировать процесс погрузки (законы изменения U(t), X(t) и V(t)), сигналы АСУ (f и i). U(t) : = (U(t) + V(t)) · ed(E(i) – U(t)) — загрузка вагона увеличивается, если вагон не полон, и останавливается и сбрасывается в ноль, если вагон загружен до нормы E(i); f : = not(ed(E(i) – U(t))) — сигнал машинисту электровоза: «продерни состав» ; i : = i + f — счетчик вагонов увеличивается в момент продергивания состава; X(t) : = X(t) – V(t) — уровень сырья в бункере понижается; a : = k · X(t) — чем меньше уровень X, тем медленнее высыпается сырье, так как верхние слои меньше давят на нижние; V(t) : = a · B — интенсивность поступления груза в вагон из бункера; B : = ed(3 – i + 1) · ed(X(t)) — сырье поступает в вагон, если его номер не больше третьего и сырье в бункере есть. На основе построенной модели можно решить ряд задач, например, определить время, за которое будет загружен весь состав, или выяснить другие какие-то другие вопросы. В общем случае, то, какая задача будет решаться на модели, во многом зависит от целей человека, использующего эту модель.
 Роль моделирования Построив модель, исследователь может: • прогнозировать свойства и поведение объекта как внутри области, в которой построена модель, так и (при обоснованном применении) за её пределами (прогнозирующая роль модели); • управлять объектом, отбирая наилучшие воздействия путём испытания их на модели (управляющая роль); • познавать явление или объект, модель которого он построил (познавательная роль модели); • получать навыки по управлению объектом путём использования модели как тренажёра или игры (обучающая роль); • улучшать объект, изменяя модель и испытывая её (проектная роль).
Роль моделирования Построив модель, исследователь может: • прогнозировать свойства и поведение объекта как внутри области, в которой построена модель, так и (при обоснованном применении) за её пределами (прогнозирующая роль модели); • управлять объектом, отбирая наилучшие воздействия путём испытания их на модели (управляющая роль); • познавать явление или объект, модель которого он построил (познавательная роль модели); • получать навыки по управлению объектом путём использования модели как тренажёра или игры (обучающая роль); • улучшать объект, изменяя модель и испытывая её (проектная роль).

