Понятие математической модели сигнала Математические модели детерминированных

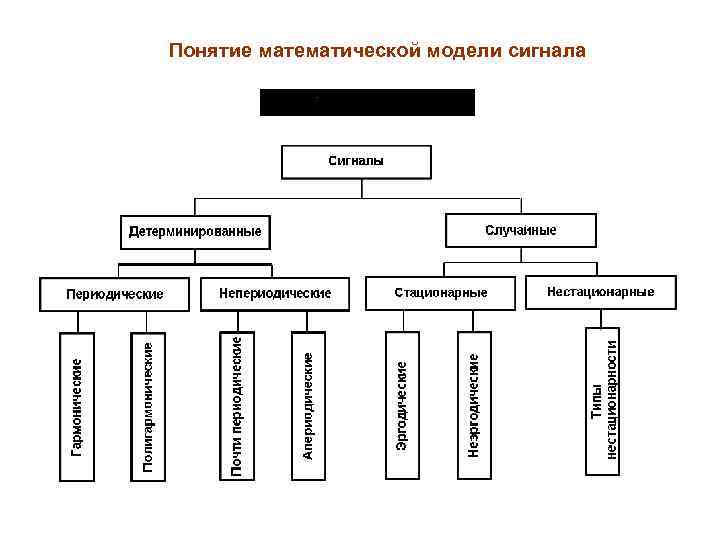
Понятие математической модели сигнала

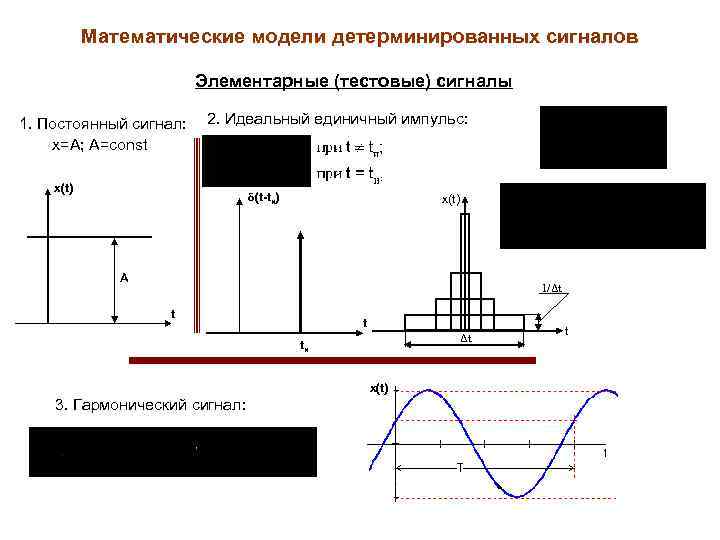Математические модели детерминированных сигналов Элементарные (тестовые) сигналы 1. Постоянный сигнал: x=A; A=const 2. Идеальный единичный импульс: x(t) δ(t-tи) x(t) А 1/Δt t t Δt tи x(t) 3. Гармонический сигнал: t

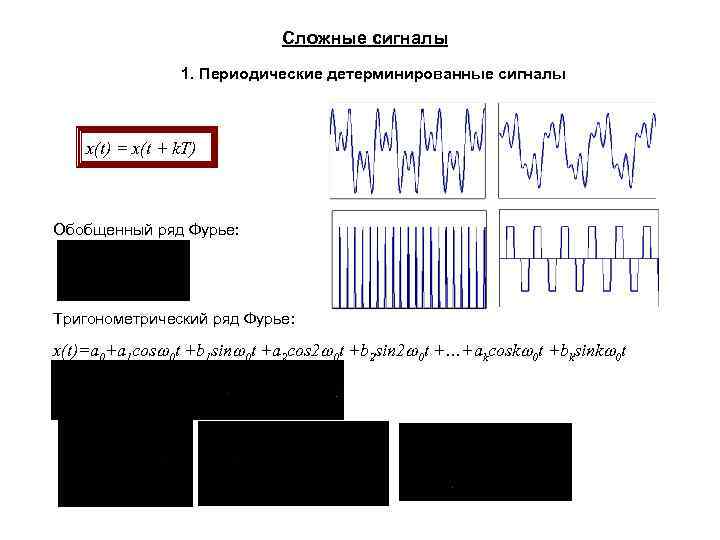Сложные сигналы 1. Периодические детерминированные сигналы x(t) = x(t + k. T) Обобщенный ряд Фурье: Тригонометрический ряд Фурье: x(t)=a 0+a 1 cos 0 t +b 1 sin 0 t +a 2 cos 2 0 t +b 2 sin 2 0 t +…+akcosk 0 t +bksink 0 t

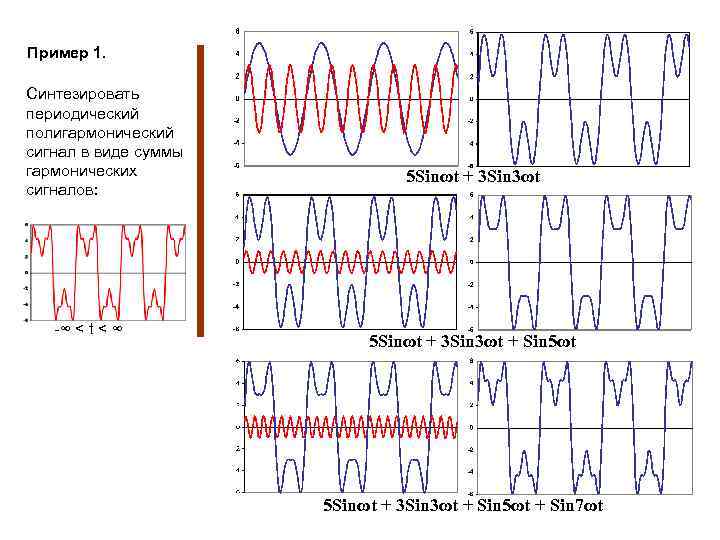Пример 1. Синтезировать периодический полигармонический сигнал в виде суммы гармонических сигналов: -∞ < t < ∞ 5 Sinωt + 3 Sin 3ωt + Sin 5ωt + Sin 7ωt

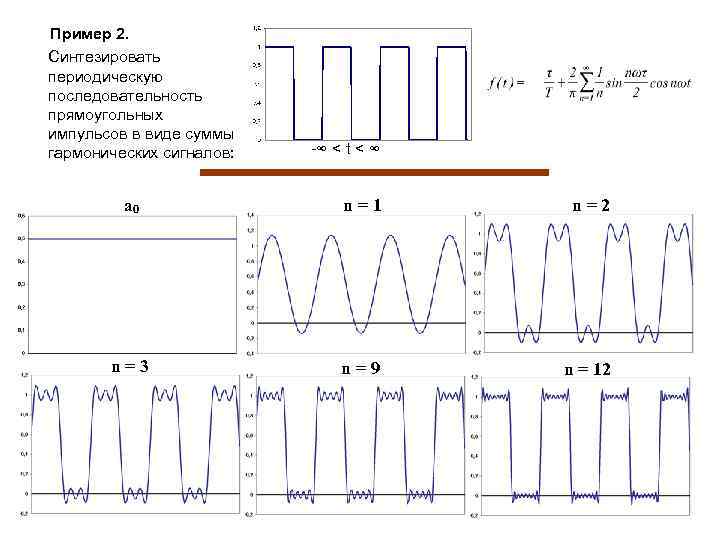Пример 2. Синтезировать периодическую последовательность прямоугольных импульсов в виде суммы гармонических сигналов: -∞ < t < ∞ а 0 n=1 n=2 n=3 n=9 n = 12

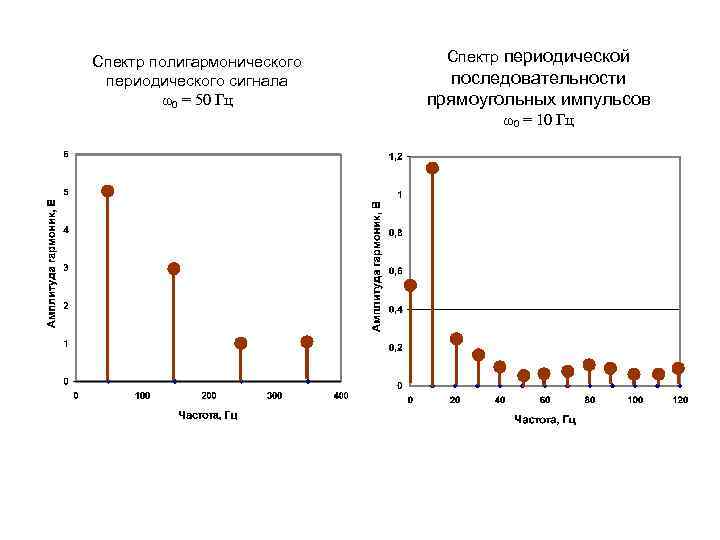Спектр полигармонического периодического сигнала ω0 = 50 Гц Спектр периодической последовательности прямоугольных импульсов ω0 = 10 Гц

Эквивалентные формы ряда Фурье: 1 2

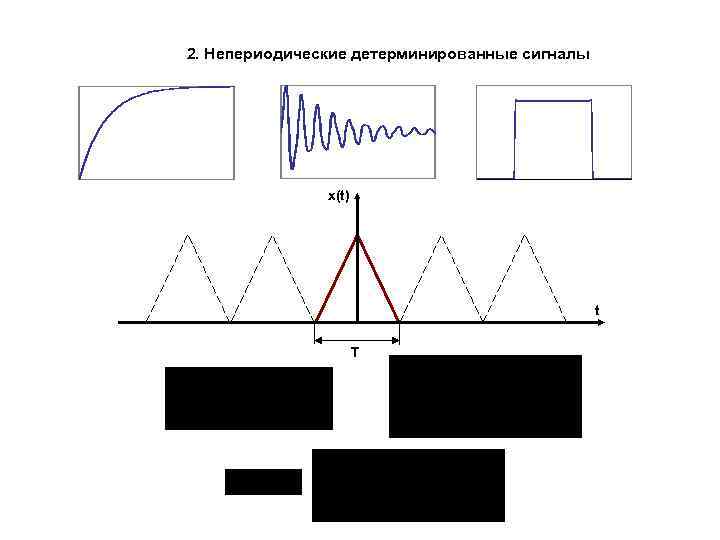2. Непериодические детерминированные сигналы x(t) t Т

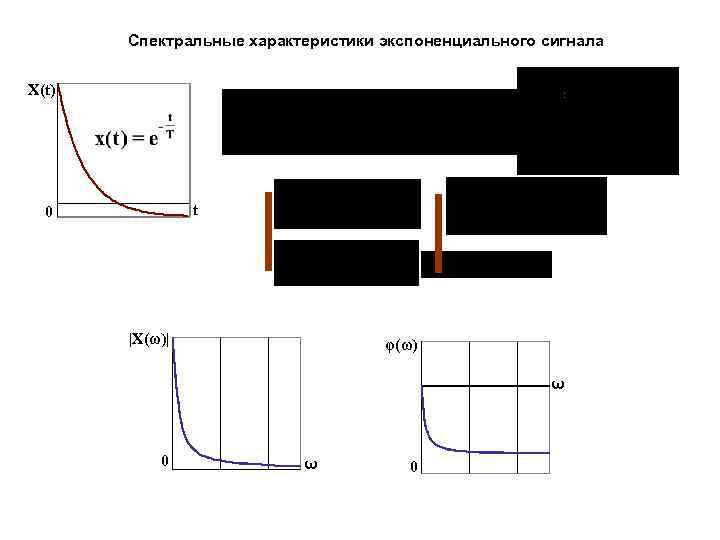Спектральные характеристики экспоненциального сигнала ∞ X(t) 0 t 0 |X(ω)| φ(ω) ω 0

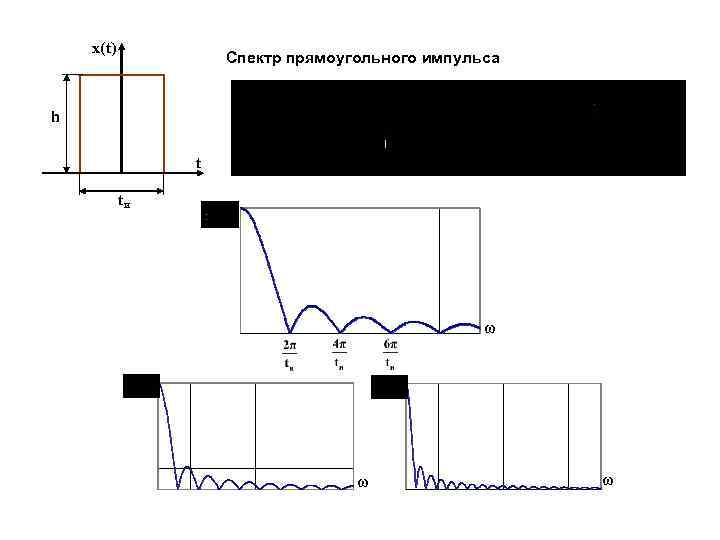x(t) Спектр прямоугольного импульса h t tи ω ω ω

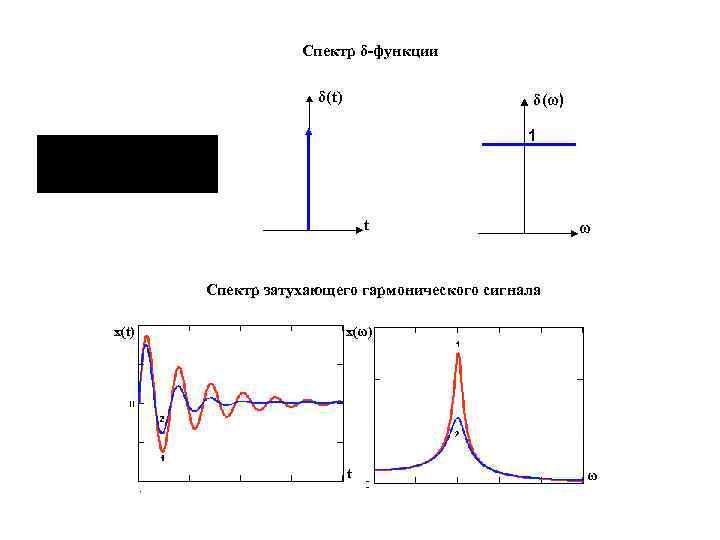Спектр δ-функции δ(t) δ(ω) 1 t ω Спектр затухающего гармонического сигнала x(t) x(ω) t ω

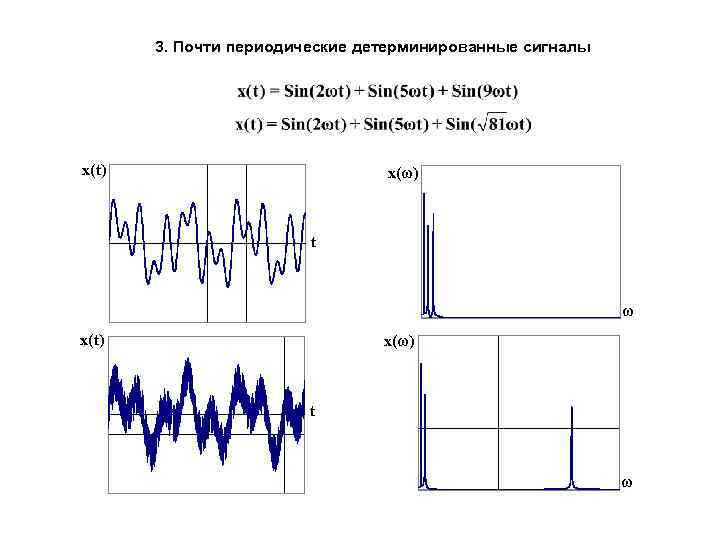3. Почти периодические детерминированные сигналы x(t) x(ω) t ω

Свойства преобразования Фурье 1. Суммирование функций: 2. Смещение функции по аргументу: 3. Изменение масштаба аргумента: 4. Дифференцирование функции: 5. Интегрирование функции: 6. Свертка функций: 7. Обратимость:

Свойства преобразования Фурье