ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ Способ снижения вероятности ошибок приеме – введение избыточности в передаваемую информацию. Варианты введения избыточности: - помехоустойчивое кодирование; - многократная передача информации; - одновременная передача информации по нескольким параллельно работающим каналам. Помехоустойчивое кодирование - самый оптимальный способ. Применяется для обнаружения и исправления ошибок в сигнале при его передаче по каналам связи. Предполагает введение в передаваемое сообщение проверочных разрядов, формируемых в устройствах защиты от ошибок: кодере – на передающей стороне, декодере – на приемной. Избыточность позволяет отличить разрешенную и запрещенную (искаженную за счет ошибок) комбинации приеме.
Помехоустойчивый код характеризуется тройкой чисел (n, k, dmin): n – общее число разрядов кодовой комбинации (n = k + r); k – число информационных разрядов, r – число проверочных разрядов. Соответственно, – количество возможных кодовых комбинаций; – количество разрешенных кодовых комбинаций (N M); Расстояние между двумя кодовыми комбинациями – расстояние по Хэммингу – d. Минимальное расстояние по Хэммингу для данной совокупности разрешенных кодовых комбинаций dmin называют кодовым расстоянием dk
Связь исправляющей способности кода с dmin Количество обнаруживаемых ошибок: где – кратность ошибки (число искажённых разрядов). Если произошла ошибка в одном разряде, то она называется однократной, в двух разрядах – двукратной и т. д. Количество исправляемых ошибок: Количество единиц в коде называют весом кодовой комбинации. Например, кодовая комбинация 1100101: значность n = 7, вес V = 4.
Для указания разрядов кодовой комбинации, в которых произошли ошибки, используется понятие вектор ошибки Вектор ошибки n-разрядного кода – это n-разрядная комбинация, где единицы указывают положение разрядов искажённых символов. Например, = 0101, значит искажены символы во втором и четвертом разрядах. Вес вектора ошибки характеризует кратность ошибки Исходная неискажённая комбинация состоит из суммы по модулю 2 искажённой комбинации и вектора ошибки: a = a’
Геометрическое представление кодов Представление кодов с помощью матриц САМОСТОЯТЕЛЬНО
Пример Код задан производящей (генераторной) матрицей: Параметры кода: n – длина кодовой комбинации (количество столбцов в матрице), n = 6. Каждая строка матрицы [G] состоит из k информационных символов и r проверочных:
![Разбиваем [G] на 2 части так, чтобы слева осталась единичная матрица; k равно количеству](https://present5.com/presentation/3/8284840_132529327.pdf-img/8284840_132529327.pdf-7.jpg "Разбиваем [G] на 2 части так, чтобы слева осталась единичная матрица; k равно количеству")
Разбиваем [G] на 2 части так, чтобы слева осталась единичная матрица; k равно количеству столбцов в этой единичной матрице (k = 3). a 1 a 2 a 3 b 4 b 5 b 6 – разряды кодовых комбинаций: a – информационные b – проверочные , Ek R Ek – единичная подматрица k-го (3 -го) порядка; R – проверочная подматрица. Определим N – количество возможных кодовых комбинаций длиной n: Определим М – количество разрешенных кодовых комбинаций:
Построим проверочную матрицу. Она состоит из двух подматриц: RТ Еn-k где RТ – транспонированная матрица R; Еn-k – единичная подматрица порядка n-k. Запишем уравнения проверок. В уравнение входят только те разряды, которым соответствуют единицы в соответствующих строках матрицы [H]:
Составим таблицу исправлений (синдромов): Синдром S 1 Конфигурация синдрома Ошибочная позиция S 2 S 3 101 110 011 a 2 a 3 Кодовое расстояние dmin равно числу единиц в строке матрицы [G] с минимальным весом: dmin = 3. Количество обнаруживаемых ошибок (кратность ошибки) определяется из неравенства: , где – кратность ошибки. 2. Таким образом, если в кодовой комбинации произошло одновременно две ошибки, то код позволит их обнаружить.
Количество исправляемых ошибок: 1. Таким образом, код может исправить только одиночную ошибку (ошибку в одном разряде).
Схема кодера Суммирование и вычитание по модулю два – операции эквивалентные. Поэтому алгоритм формирования контрольных символов можно получить, переписав уравнения проверок: . Кодер состоит из n-разрядного универсального регистра сдвига и n – k = r сумматоров по модулю два (в нашем случае сумматора три). В регистр можно одновременно записать k информационных символов (в нашем случае три). После этого формируются контрольные символы, согласно уравнениям проверок.
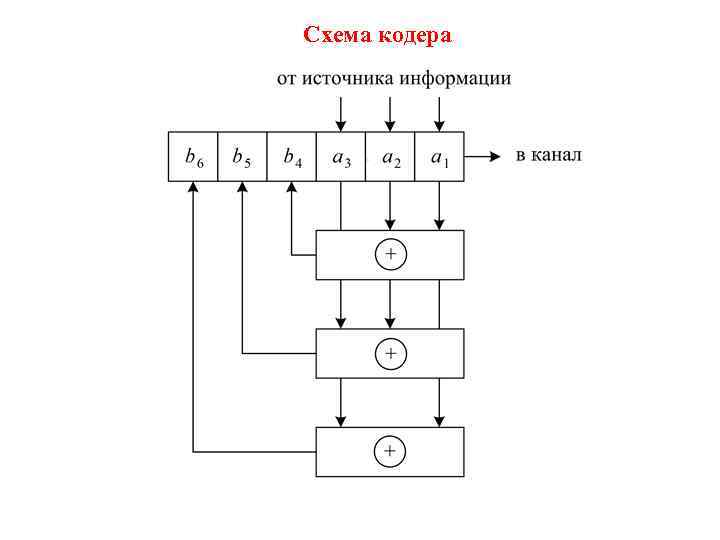
Схема кодера
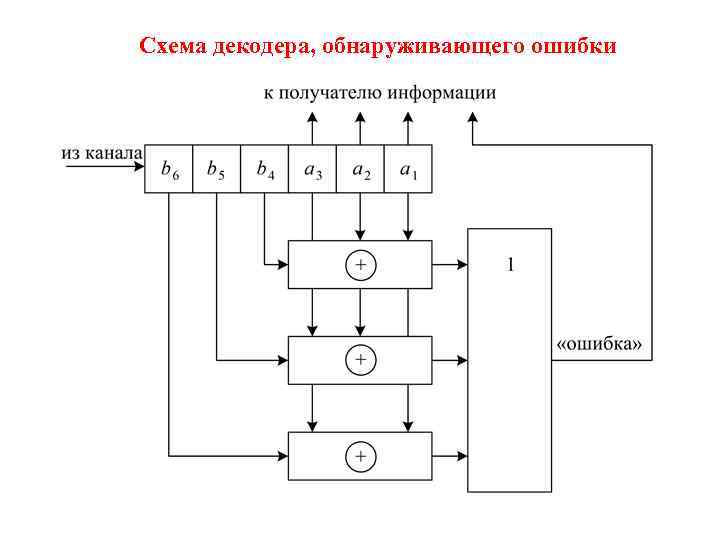
Схема декодера, обнаруживающего ошибки
Схема декодера, обнаруживающего ошибки, также составляется по уравнениям проверок. Регистр также n-разрядный. Сумматоров столько же, сколько и в схеме кодера, только у каждого из них на один вход больше. Если ошибок не было, то уравнения проверок выполняются и на входах и выходе схемы «ИЛИ» – нули. . Если хотя бы в одной позиции была ошибка, то хотя бы на одном из входов и выходе появится « 1» , что сигнализирует об ошибке.
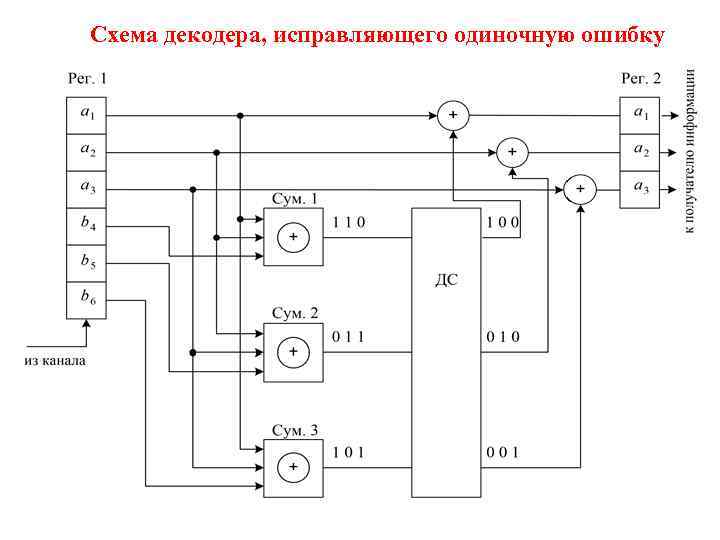
Схема декодера, исправляющего одиночную ошибку
Схема декодера, исправляющего одиночную ошибку Кодовые комбинации из канала в последовательном режиме записываются в регистр Рег. 1. С помощью трех сумматоров по модулю два осуществляется проверка на наличие ошибки в информационных разрядах, согласно уравнениям проверок. В зависимости от номера разряда, в котором произошла ошибка, на выходах 1 -го, 2 -го и 3 -го сумматоров будут различные кодовые комбинации. Если ошибка произошла в разряде a 1, то на выходах трех сумматоров появится комбинация 101, т. к. a 1 подается на первый и третий сумматоры; если ошибка в разряде a 2 – комбинация 110 (a 2 подается на первый и второй сумматоры); если ошибка в разряде a 3 – комбинация 011 (a 3 подается на второй и третий сумматоры). Если ошибки нет, то кодовая комбинация будет 000. Эти кодовые комбинации называются синдромами ошибок.
Схема декодера, исправляющего одиночную ошибку Анализ синдромов осуществляет дешифратор синдромов (ДС). Он имеет три выхода. При наличии ошибки « 1» появится на том выходе, в какой позиции произошла ошибка. На остальных выходах – нули. Ошибка исправляется следующим образом. Для исправления ошибки нужно знать номер позиции, в которой она произошла. Как следует из таблицы истинности для двухвходового сумматора по модулю «два» , если на одном входе « 0» , то для второго входа сумматор работает как повторитель. Если же на одном из входов « 1» , то для второго входа он работает как инвертор. Очевидно, что для того, чтобы исправить ошибку в двоичном коде, надо ошибочный разряд инвертировать. Например, произошла ошибка в разряде a 1. Синдром ошибки будет 101, на выходе дешифратора синдромов – 100. Поэтому второй и третий разряды инвертированы не будут, а первый разряд будет инвертирован. Таким образом, в регистр Рег. 2 запишется исправленная информационная кодовая комбинация, которую примет получатель информации.
Скачать презентацию ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ Способ снижения вероятности ошибок приеме –
5. Помехоустойчивое кодирование.ppt