Полтавський національний технічний університет імені Юрія Кондратюка Кафедра

Полтавський національний технічний університет імені Юрія Кондратюка Кафедра залізобетонних і кам’яних конструкцій та опору матеріалів yx у σx σy xy σx xy yx σy x Мультимедійний курс лекцій з ОПОРУ МАТЕРІАЛІВ Частина 1 (модуль 1 і 2) Полтава - 2012

Мультимедійний курс лекцій з опору матеріалів для студентів напрямів підготовки 6. 050502 “Інженерна механіка”, 6. 050503 “Машинобудування”, 6. 070106 “Автомобільний транспорт” (частина 1). – Полтава: Полт. НТУ, 2012. – 75 слайдів. Укладачі: к. т. н. , доц. В. В. Муравльов, к. т. н. , доц. А. В. Гасенко Відповідальний за випуск: завідувач кафедри залізобетонних і кам’яних конструкцій та опору матеріалів А. М. Павліков, доктор техн. наук, професор Рецензент: О. Г. Фенко кандидат техн. наук, доцент кафедри залізобетонних і кам’яних конструкцій та опору матеріалів Затверджено науково-методичною радою університету протокол № 5 від 25 січня 2012 р. Авторська редакція Комп’ютерна верстка: А. В. Гасенко 41. 07. 02. 01 2

Зміст n n n МОДУЛЬ 1 Лекція 1. Задачі науки про опір матеріалів. Класифікація тіл по геометричних ознаках. Об'єкти вивчення в курсі з опору матеріалів. Зв'язок науки про опір матеріалів з іншими науками. Реальний об'єкт та розрахункова схема. Основні гіпотези. Зовнішні сили та класифікація навантажень. Визначення внутрішніх зусиль. Метод уявних перерізів. Лекція 2. Розтяг та стиск прямого бруса. Повздовжні сили, їх епюри. Напруження в поперечному і нахиленому під довільним кутом перерізі бруса. Повздовжні та поперечні деформації. Закон Гука при розтязі та стиску. Лекція 3. Механічні характеристики матеріалів при розтязі та стиску. Розтяг та стиск пластичних матеріалів. Основні механічні властивості. Особливості деформування та зруйнування пластичних матеріалів. Розтяг та стиск крихких матеріалів, їх основні характеристики. Лекція 4. Поняття про повзучість, релаксацію та тривалу міцність. Потенційна енергія деформації при розтязі та стиску. Повна та питома робота, що витрачається на деформування матеріалів. Особливості їх поведінки під навантаженням. Вплив швидкості навантаження, температури та других факторів на характеристики міцності матеріалів. Лекція 5. Розрахунки на міцність і жорсткість при розтязі та стиску. Основні поняття про міцність, надійність, довговічність конструкцій. Методи розрахунків по допустимих напруженнях, допустимих навантаженнях. Основні типи задач в опорі матеріалів. Поняття концентрації та коефіцієнта концентрації. Лекція 6. Врахування власної ваги при розтязі та стиску. Поняття про брус рівного опору. Переміщення під дією власної ваги. Лекція 7. Основні поняття про геометричні характеристики перерізів. Статичний момент інерції. Центр ваги фігури. Моменти інерції простих фігур. Лекція 8. Зміна осьових та відцентрових моментів при паралельному переході від центральних осей до довільних. Зміна осьових та відцентрових моментів при повороті координатних осей. Поняття про головні осі, головні центральні осі. Визначення головних моментів та моментів інерції для складних перерізів. Моменти опору. Радіус інерції. МОДУЛЬ 2 Лекція 9. Основні поняття про напружений стан тіла в точці. Способи визначення напруженого стану. Закон парності дотичних напружень. Лекція 10. Типи напружених станів тіла в точці. Лінійний напружений стан. Зміна напружень при повороті площадок. Визначення головних напружень через напруження взаємно перпендикулярних площадок. Графічне відображення плоского напруженого стану. Траєкторія головних напружень. Лекція 11. Поняття про об’ємний напружений стан. Об’ємна деформація. Зв'язок між напруженням та деформаціями. Загальний закон Гука. Залежність між пружними постійного матеріалу. Відносна зміна об'єму. Потенційна енергія пружної деформації. Питома енергія та енергія зміни об'єму та форми. Лекція 12. Призначення теорії міцності. Поняття про еквівалентне напруження. Класифікація теорій міцності. Теорія Мора, енергетична теорія та інші. Загальні відомості про нові теорії та гіпотези міцності та пластичності. 3

n n n 1. 2. 3. 4. 5. 1. 2. 3. 4. 5. Лекція 13. Напруження і деформації при зсуві. Чистий зсув. Розрахунки на міцність і умови міцності при зсуві. Лекція 14. Основні типи опор і балок. Чистий і поперечний згин. Внутрішні зусилля при згині. Диференціальні залежності. Побудова епюр поперечних сил і згинальних моментів. Лекція 15. Нормальні та дотичні напруження при згині. Основні припущення. Залежність між згинаючим моментом та кривизною осі зігнутого брусу. Жорсткість при згині. Напружений стан при згині. Розрахунок при згині на міцність по допустимих напруженнях. Потенційна енергія деформації при згині. Лекція 16. Зовнішні сили, що визивають кручення бруса. Кручення прямого брусу круглого поперечного перерізу. Основні припущення. Напруження в поперечних перерізах бруса. Кут закручення. Жорсткість та міцність при крученні. Основні результати теорії кручення брусів прямокутного перерізу. Кручення стержнів, перерізи яких складаються з декількох вузьких прямокутників. Поняття про мембранну аналогію. Лекція 17. Розрахунки циліндричних кругових пружин. Потенційна енергія деформації. Умови міцності та жорсткості при крученні пружин. Лекція 18. Статична невизначеність стержневих систем. Статично невизначені задачі при розтязі та стиску, температурному впливу, конструкційних особливостях та інше. Порогові навантаження статично невизначених стержневих систем та напруження в них. Рекомендована література Смирнов А. Ф. Опір матеріалів. – М. , 1976. Писаренко Г. С. Опір матеріалів. – К. , 1986. Біляєв Н. М. Опір матеріалів. – М. : Наука, 1976. Качурин В. К. , Біляєв Н. М. та ін. Збірник задач з опору матеріалів / Під ред. В. К. Качурина. – М. : Наука, 1972. Писаренко Г. С. , Яковлев А. П. та ін. Довідник з опору матеріалів. – К. Наукова думка, 1975. Методичне забезпечення Методичні вказівки та завдання до виконання розрахунково-проектувальних робіт із курсу “Опір матеріалів” для студентів електромеханічного факультету / Укладачі: К. І. Залужна, В. А. Кириченко, В. В. Муравльов, В. М. Чередніков – Полтава : Полт. НТУ, 2005. – 30 с. Методичні вказівки та завдання до виконання курсової роботи із курсу “Опір матеріалів” для студентів електромеханічного факультету / Укладачі: К. І. Залужна, В. А. Кириченко, В. В. Муравльов, В. М. Чередніков. – Полтава : Полт. НТУ, 2006. – 28 с. Журнал лабораторних робіт з опору матеріалів / Укладачі: В. А. Кириченко, В. В. Муравльов, В. М. Чередніков. – Полтава : Полт. НТУ, 2004. – 33 с. Методичні вказівки до виконання лабораторних робіт з опору матеріалів для студентів усіх напрямів підготовки / Укладачі: А. В. Гасенко, О. Г. Фенко. – Полтава : Полт. НТУ, 2011. – 39 с. Методичні вказівки для самостійної роботи з дисципліни “Опір матеріалів” для студентів денної та заочної форм навчання за спеціальністю “Технологія машинобудування” / Укладачі: О. Г. Фенко. – Полтава: Полт. НТУ, 2005. – 29 с. 4

Лекція 1 Вступ Опір матеріалів є частиною більш загальної науки - механіки твердого деформівного тіла, в яку входять: теорія пружності, теорії пластичності і повзучості, теорія споруд, будівельна механіка, механіка руйнування та ін. Завданням опору матеріалів є вивчення методів розрахунку найпростіших елементів конструкцій і деталей машин на міцність, жорсткість і стійкість. n Механіка твердого тіла, що деформується Механіка підземних споруд Теорія споруд Будівельні конструкції Будівельна механіка Опір матеріалів Теорія пластичності і повзучості Теорія пружності Деталі машин Механіка ґрунтів Механіка руйнування Прикладна механіка Міцністю називається здатність елемента конструкції чинити опір дії прикладених до нього сил не руйнуючись. Жорсткістю називається здатність елемента конструкції чинити опір дії прикладених до нього сил, отримуючи лише малі пружні деформації. Стійкістю називається здатність елемента конструкції зберігати первинну форму рівноваги під дією прикладених сил. Реальні тіла не є абсолютно твердими і під дією прикладених до них сил змінюють свою первинну форму і розміри, тобто деформуються. Деформації тіла, що зникають після зняття зовнішніх сил, називаються пружними, а не зникають - залишковими або пластичними. Визначення розмірів деталей або зовнішніх навантажень, при яких виключається можливість руйнування деталей, є метою розрахунку на міцність. Визначення розмірів деталей або зовнішніх навантажень, при яких виключається можливість появи неприпустимих з точки зору нормальної роботи конструкції деформацій цих деталей, є метою розрахунку на жорсткість. n n Реальний об'єкт і розрахункова схема Реальний об'єкт, звільнений від несуттєвих особливостей, які не впливають помітним чином натакі як скло і смоли. Ізотропними є аморфні матеріали, роботу системи в цілому, називається розрахунковою схемою. Перехід від реального об'єкта до розрахункової схеми здійснюється шляхом схематизації властивостей Анізотропними є пластмаси, текстоліт матеріалу, системи прикладених сил, геометрії реального об'єкта, типів опорних пристроїв і т. д. і т. п. Метали є полікристалічний тілами, що складаються з великої Схематизація властивостей матеріалу кількості зерен, розміри яких дуже малі (близько 0, 01 мм). Реальні матеріали володіють різноманітними фізичними властивостями є характерною для кожного з них структурою. З метою спрощення Кожне зерно і анізотропним, але внаслідок малих розмірів зерен розрахунків в опорі матеріалів використовуються наступні припущення про властивості матеріалу. і безладного їх розташування метали проявляють властивість ізотропії. 1. Матеріал вважається однорідним, якщо його властивості у всіх точках однакові. 2. Матеріал вважається ізотропним, якщо його властивості у всіх напрямках однакові. 5

Лекція 1 (продовження – 1. 2) 3. Матеріал має властивість ідеальної пружності, внаслідок якої деформоване тіло повністю відновлює свою форму і розміри після зняття навантаження незалежно від величин навантажень і температури тіла. 4. Форма і розміри пружного тіла змінюються прямо пропорційно зміні навантажень, тобто підпорядковується закону Гука (1660 р. ). 5. Матеріал має властивість суцільності, тобто здатністю суцільно (без порожнин) заповнювати простір, обмежений поверхнею тіла. Внаслідок цього матеріал вважається безперервним, що дозволяє використовувати для визначення напружень і деформацій математичний апарат диференціального й інтегрального числення. 6. Пружні тіла є відносно жорсткими, завдяки чому переміщення точок тіла дуже малі в порівнянні з розмірами самого тіла. Ця гіпотеза служить підставою для використання при розрахунку початкових (вихідних) розмірів тіла (по недеформованій схемі). Схематизація геометрії реального об'єкта - спрощує геометрію реально існуючих тіл, що складають конструкцію. Більшість споруд, механізмів і машин можна розчленувати на окремі тіла простої геометричної форми: Брус - тіло, два розміри якої малі в порівнянні з третім (стрижні, стійки, вали, балки). Брус може мати різну форму поперечного перерізу (круглий, кільцевий, прямокутний, коробчастий, двотавровий та ін. ) Поперечний переріз утворюється при розрізі бруса площиною, перпендикулярної поздовжньої осі, а поздовжня вісь є лінією, що з'єднує центри ваги поперечних перерізів, і може бути прямою або криволінійної. Брус є основним об'єктом, що розглядається в курсі опору матеріалів. Наступні тіла є об'єктами розгляду в інших розділах механіки твердого тіла, що деформується (теорія пластин та оболонок, теорія пружності та ін): Оболонка, пластина - тіло, один вимір якого малий в порівнянні з двома іншими (тонкостінні резервуари, оболонки перекриття, плити, стінки). Масив - тіло, всі три виміри якого мало відрізняються один від одного (фундаментні блоки, кулька підшипника, тіло гравітаційної греблі). n Схематизація силового впливу - представляє модель механічної дії зовнішніх сил на об'єкт від інших тіл або середовищ. До зовнішніх сил належать також і реакції зв'язків, що визначаються методами теоретичної механіки. Схематизація силового впливу зводиться до розгляду трьох типів навантаження: Зосереджена сила - сила, що розглядалася в курсі теоретичної механіки як вектор, що характеризується модулем (величиною), напрямком дії і точкою прикладання. Тут така сила є умовною, оскільки механічна взаємодія деформованих тіл не може здійснюватися в точці (площа контакту не дорівнює нулю). Умовність полягає в тому, що в разі малості площини контакту у порівнянні з розмірами об'єкта, сила вважається прикладеної в точці. Якщо ж визначаються контактні напруження, наприклад, в головці рейки, то враховується фактичний розподіл навантаження на рейку по площадці контакту, розміри якої залежать від величини стискаючої сили (рівнодійної тиску). Зосереджена сила вимірюється в ньютонах (Н). Об'ємні сили - сили, розподілені по об'єму (сили тяжіння, сили інерції), прикладені в кожній частині об’єму. Для цих сил схематизація часто полягає в завданні простого закону зміни цих сил за об’ємом. Об'ємні сили визначаються їх інтенсивністю, як границі відношення рівнодіючої сили в розглянутому елементарному об’ємі до величини цього об’єму, що прагне до нуля: і вимірюються в Н/м 3. n 6

Лекція 1 (продовження – 1. 3) Поверхневі сили - сили, розподілені по поверхні (тиск рідини, газу або іншого тіла), що характеризуються інтенсивністю тиску, як границя відношення рівнодіючої сили на розглянутій елементарній площадці до величини площі Цієї площадки, що прагне до нуля: Лінійно розподілене навантаження - сили, розподілені по деякій лінії (довжині), що характеризується інтенсивністю навантаження, як границя відношення рівнодіючої сили на розглянутій елементарній довжині лінії до величини довжини цієї лінії, Що прагне до нуля: і вимірюються в Н/м 2. Для цих сил схематизація часто полягає в завданні простого закону зміни цих сил по поверхні. і вимірюються в Н / м. Для цих сил умовність полягає у представленні області контакту у вигляді лінії нульової товщини. Характер зміни часто задається у вигляді простого закону (постійного, лінійного). F A F q=q(s) s За характером впливу на споруди зовнішні сили діляться на статичні і динамічні. Динамічне навантаження швидко змінюється в часі (при русі рухомого складу, коливання, удар). При повільній зміні навантаження, можна знехтувати силами інерції і деформаціями, що виникають в об'єкті, і таке навантаження може умовно вважатися статичним. За час дії на споруди навантаження ділиться на постійне (вага несучих конструкції будівлі, вага мостового полотна) і тимчасове (навантаження від рухомого складу, вітрове або снігове навантаження). Тимчасові навантаження регламентуються спеціальними документами (СНи. П, ТУ). n Внутрішні зусилля. Під дією зовнішніх сил на об'єкт відбувається зміна відстаней між частинками (атомами) розглянутого тіла і сил взаємодії між ними. В результаті виникають так звані внутрішні сили, які можна визначити методом перерізів : 1. Нехай брус під дією сил F 1, F 2, . . . перебуває в рівновазі. Для даного об'єкту F 3 My задовольняються рівняння рівноваги: 2. Проведемо переріз площиною, що співпадає з Rz Qy поперечним перерізом брусу, в якому необхідно знайти Rx RN Mz внутрішні сили. O Rx Або, як легко можна довести: z Qy 3. Відкинемо одну з частин (наприклад, ліву) і замінимо її дію на частину бруса, що M 0 залишилась, сукупністю реактивних сил, розподілених деяким чином по поверхні Mx поперечного перерізу. F 2 F 4 4. Отриману систему внутрішніх сил можна спростити приведенням до головного вектору і x головного моменту, вибравши як центр приведення центр ваги поперечного перерізу. 5. Розкладемо головний вектор і головний момент на складові по осях x, y, z: Rx, Ry, Rz і Mx, My, Mz. 6. Отримані компоненти мають в опорі матеріалів спеціальні назви, що відповідають видам деформації: Rz = N - поздовжняа сила, Rx = Qx, Ry = Qy - поперечні сили і Mz - крутний момент, Mx, My - згинальні моменти. 7. Оскільки залишена частина бруса повинна залишитися в рівновазі, отримані внутрішні силові фактори можуть бути визначені: з рівнянь рівноваги, складених для цієї частини: F 1 y 7

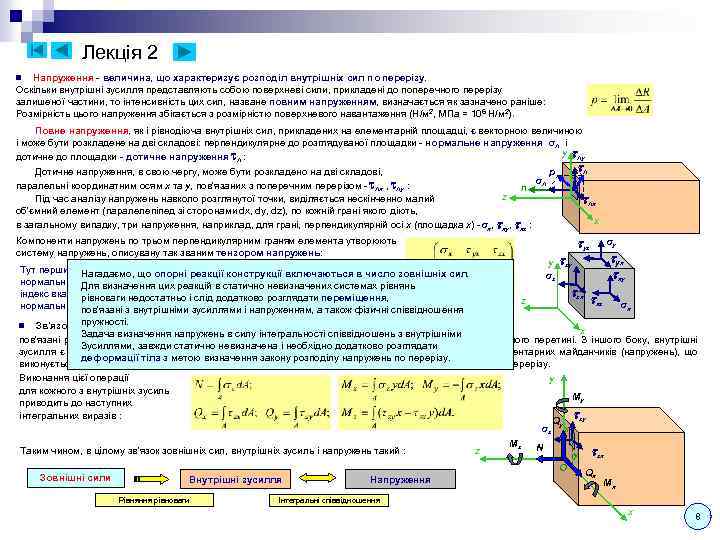Лекція 2 Напруження - величина, що характеризує розподіл внутрішніх сил по перерізу. Оскільки внутрішні зусилля представляють собою поверхневі сили, прикладені до поперечного перерізу залишеної частини, то інтенсивність цих сил, назване повним напруженням, визначається як зазначено раніше: Розмірність цього напруження збігається з розмірністю поверхневого навантаження (Н/м 2, МПа = 106 Н/м 2). n Повне напруження, як і рівнодіюча внутрішніх сил, прикладених на елементарній площадці, є векторною величиною і може бути розкладене на дві складові: перпендикулярне до розглядуваної площадки - нормальне напруження σn і y ny дотичне до площадки - дотичне напруження n : n Дотичне напруження, в свою чергу, може бути розкладено на дві складові, p σn паралельні координатним осям x та y, пов'язаних з поперечним перерізом - nx , ny : n z Під час аналізу напружень навколо розглянутої точки, виділяється нескінченно малий об'ємний елемент (паралелепіпед зі сторонами dx, dy, dz), по кожній грані якого діють, в загальному випадку, три напруження, наприклад, для грані, перпендикулярній осі x (площадка x) -σx, xy, xz : x yz Компоненти напружень по трьом перпендикулярним граням елемента утворюють систему напружень, описувану так званим тензором напружень: Тут перший стовпець представляє компоненти напружень на площадках, число зовнішніх сил. Нагадаємо, що опорні реакції конструкції включаються в нормальних до осі x, другий і третій - до осі статично невизначених системах рівнянь Для визначення цих реакцій в y та z відповідно. перший індекс вказуєрівноваги недостатньо ідругий - напрям. розглядати переміщення, площадку ("місце") дії, слід додатково Для нормальних напружень індекси збігаються і один напруженням, а також фізичні співвідношення пов'язані з внутрішніми зусиллями і індекс опускається. nx y σz z σy yx xy zy zx xz σx пружності. Зв'язок внутрішніх зусиль і напружень - Внутрішні зусилля в перерізі, як було показано вище, x Задача визначення напружень в силу інтегральності співвідношень з внутрішніми пов'язані рівняннями рівноваги з зовнішніми силами, прикладеними до залишеної частини бруса при його перетині. З іншого боку, внутрішні Зусиллями, завжди статично невизначена і необхідно додатково розглядати зусилля є результат приведення до центру поперечного перерізу внутрішніх сил, прикладених до елементарних майданчиків (напружень), що деформації тіла з метою визначення закону розподілу напружень по перерізу. виконується додаванням, яке для елементарних сил зводиться до інтегрування за площею поперечного перерізу. Виконання цієї операції y для кожного з внутрішніх зусиль My приводить до наступних zy інтегральних виразів : Q σz y x Mz N Таким чином, в цілому зв'язок зовнішніх сил, внутрішніх зусиль і напружень такий : z y zx O Qx Зовнішні сили Напруження Внутрішні зусилля M n x Рівняння рівноваги Інтегральні співвідношення x 8

Лекція 2 (продовження – 2. 2) Переміщення – перехід точок тіла в нове положення внаслідок зміни форми і розмірів тіла під дією навантаження. Повне переміщення точки в просторі розкладається на компоненти u, v і w, паралельні осям x, y і z, відповідно. Переміщення розглядуваної точки залежить від деформації всіх навантажених областей тіла і включає в себе переміщення як жорсткого цілого ненавантажених областей. Таким чином, переміщення не може характеризувати ступінь деформування навколо розглядуваної точки. ■ Деформація в точці - міра деформування матеріалу навколо точки. Виділимо в даній точці тіла елементарний об’єм (паралелепіпед зі сторонами dx, dy, dz) і розглянемо його можливі зміни розмірів і форми. Нехай за рахунок деформації довжини його ребер отримають абсолютні видовження dx, dy та dz: dy y Відносні лінійні деформації в точці : dy z n Крім лінійних деформацій, пов'язаних зі зміною розмірів лінійних елементів, виникають кутові деформації або кути зсуву, пов'язані зі зміною форми. Наприклад, у площині xy можуть виникати малі зміни прямих кутів паралелепіпеда : x y dy xy x dx dz dx Такі кутові деформації в загальному випадку можуть мати місце у всіх трьох x площинах. Всі відносні деформації досить малі і мають для реальних матеріалів порядок ≈10 -4 -10 -3. Таким чином, сукупність відносних лінійних і кутових деформацій визначають деформований стан в точці і утворюють тензор деформацій, подібний тензора напружень: Примітка: Половинні кути зсуву використовуються з метою отримання аналогічних формул перетворення з тензором напружень. Залежно від того, які з компонент відносних деформацій мають нульове значення в даній області або для всього тіла, розрізняють такі прості види деформацій: 1. Лінійна деформація - εz ≠ 0, кути зсуву дорівнюють нулю, іншими лінійними відносними деформаціями нехтується (Характеризується абсолютним і відносним подовженням). 2. Плоска деформація - εz ≠ 0, εx ≠ 0 або εy ≠ 0, інші відносні деформації дорівнюють нулю (характеризується абсолютним і відносним звуженням площі поперечного перерізу). Ці види деформацій зазвичай реалізуються при розтязі-стиску. 3. Об'ємна деформація - εz ≠ 0, εx ≠ 0, εy ≠ 0, кути зсуву дорівнюють нулю (характеризується абсолютною і відносною зміною об’єму). 4. Чистий зсув - лінійні відносні деформації дорівнюють нулю, кути зсуву не рівні нулю (характеризується зміною форми, зміна об’єму не відбувається). Цей вид деформації також виникає при крученні. Відповідно до виду деформації спочатку послідовно вивчають такі найпростіші напружено-деформовані стани як розтяг-стиск, чистий зсув і кручення, чистий згин. Далі вивчаються більш складні - поперечний згин, складний опір, поздовжній згин. dz 9

Лекція 2 (продовження – 2. 3) ■ Визначення внутрішніх зусиль - Внутрішні зусилля визначаються методом перерізів в сукупності точок по довжині бруса з метою виявлення їх максимальних значень. Графік зміни внутрішнього зусилля по осі бруса називається епюрою. Загальний порядок побудови епюр внутрішніх зусиль: 1. Якщо необхідно, то визначаються опорні реакції так, як це робиться в курсі теоретичної механіки (обрати об'єкт, відкинути зв'язок, замінити відкинуті зв'язки реакціями, скласти рівняння рівноваги). Реакції можна не знаходити, якщо вони не входять до числа зовнішніх сил, прикладених по одну сторону від розглядуваних перерізів. З рівняння на яких навантаження або для поздовжньої сили на ділянці 1: 2. Визначається число ділянок по довжині бруса, рівноваги отримуємо виразгеометрія бруса не змінюється. Межею ділянки є будь-який Повторюємо кроки 3 та для наступних ділянок: фактор, що впливає на різку (стрибкоподібну) зміну аналізованого 4 внутрішнього зусилля (початок чи кінець бруса, перелом осі бруса, місце розташування опори, точка прикладення зовнішньої зосередженої силиділянці і визначимо поточну координату перерізу моменту, 3. Проведемо переріз II-II на другій або іншого фактора, наприклад, зосередженого і межі її початок або кінець розподіленого навантаження). z b. зміни: 0 2 3. На кожній з ділянок проводиться переріз, віддалений від початку ділянки на деякій довільній (змінній) відстані. Для II-II 4. Відкинемо ліву частину, замінимо її початку бруса і записуються межі зміни координати. кожного перерізу вказується поточна координата (z) від початку ділянки або від дію поздовжньої силою N і складемо рівняння рівноваги в проекції на вісь z: При виборі початку локальних координат на початку ділянки нижня межа завжди дорівнює нулю. 4. Для розглядуваного перерізу записується вираз рівноваги отримуємо вираз для поздовжньої сили на ділянці 2: З рівняння внутрішнього зусилля у вигляді функції від координати z, розглядаючи рівновагу залишеної частини або використовуючи встановлені визначення для обчислення внутрішнього зусилля по зовнішнім силам, розташованим по одну Аналогічно отримуємо для ділянки 3 (0 z 3 c): сторону від перерізу. 5. За отриманими виразами будується епюра зміни зусилля підстановкою верхньої і нижньої меж, і якщо необхідно, Отримані вирази показують, що поздовжня сила в перерізі дорівнює алгебраїчній сумі інших значень координат в дозволеному інтервалі, зазвичай в середині інтервалу. проекцій на вісь бруса сил, взятих по одну сторону від перерізу! Знак доданків позитивний, якщо розглянута сила виникає лише Внутрішні зусилля при розтязі-стиску - при розтязі-стиску в поперечному перерізі стержняспрямована один силовий від перерізу, тобто будучи прикладена до перерізу викликає розтягування частини бруса по інший бік фактор - поздовжня сила N. Відповідно до методу перерізів величина і напрям поздовжньої сили можуть бути знайдені з від розрізу. рівняння рівноваги в проекції на вісь, що збігається з віссю стержня, складеного для залишеної частини: n n Поздовжня сила вважається позитивною, якщо вона викликає розтяг, тобто спрямована від перерізу (у бік зовнішньої нормалі), і негативною, якщо вона викликає стиск, тобто направлено до перерізу. z 1 z 2 z 3 III I II Використовуючи отримані вирази для поздовжньої сили побудуємо епюру поздовжніх Нехай прямолінійний брус навантажений поздовжніми зосередженими силами F 1, F 2: сил: При побудові епюри N, додатні значення зазвичай відкладаються вгору від базисної лінії F 1 F 2 1. або Реакції лівої опори вертикальна. вправо, якщо вона можна не визначати, тому що в цьому прикладі можна обмежитися розглядом лише сил, прикладених = 100 к. Н. Відкладаючичастин (праворуч від перерізів). III Нехай F 1 = 250 к. Н, F 2 до правих залишених на кожній з ділянок значення поздовжньої сили в деякому I II c a b 2. вибраному масштабі отримуємо епюру N: Число ділянок - 3 NI-I 3. Проведемо переріз щона першій ділянці та розташовуються в точках прикладення зовнішніх зміни: F 1 F 2 Зверніть увагу, I-I стрибки на епюрі N визначимо поточну координату перерізу й межі її 0 z 1 a. зосереджених сил і рівні величинам цих сил. Відповідно стрибок на лівому кінці NII-II F 2 епюри дає частину, опорної її дію поздовжньої силою NI-I 4. Відкинемо ліву величинузамінимореакції. і складемо рівняння рівноваги в проекції на вісь z: NIII-III 10

Лекція 2 (продовження – 2. 4) n n n Центральний розтяг-стиск. У багатьох елементах конструкцій виникають тільки поздовжні зусилля, що викликають у них деформації розтягу або стиску (стійки, елементи ферм, тяги, троси і т. п. ). При цьому в місцях прикладення умовно зосереджених сил характер розподілу деформацій досить складний і відрізняється від розподілу деформацій на деякій відстані від цієї локальної області. Розмір цієї області дорівнює приблизно найбільшому з розмірів поперечного перерізу. Принцип Сен-Венана - Якщо сукупність деяких сил, прикладених до невеликої частини поверхні тіла, замінити статично еквівалентною системою інших сил, то така заміна не викличе суттєвих змін в умовах навантаження частин тіла, досить віддалених від місць прикладання вихідної системи сил. Як показує досвід, за межами цієї області деформації практично постійні і поперечні перерізи переміщуються паралельно своїм початковим положенням. На підставі цього вводиться гіпотеза плоских перерізів (Я. Бернуллі): Поперечні перерізи стержня, плоскі і перпендикулярні до осі стержня до деформації, залишаються плоскими і перпендикулярними після деформації. Напруження і деформації - Як було раніше сказано, задача визначення напружень завжди є статично невизначеною. Такі завдання вирішуються послідовним розглядом статичної, геометричної і фізичної сторін. В даному випадку маємо статичне рівняння, що зв'язує внутрішнє зусилля - поздовжню силу з напруженням: n Для обчислення інтеграла необхідно знати закон зміни напружень по перерізу. Цей закон можна встановити вивченням безпосередньо досліджуваних переміщень (деформацій). Оскільки приймається гіпотеза плоских перерізів, то при відсутності зовнішнього розподіленого поздовжнього навантаження, деформації постійні по перерізу і по довжині стержня (геометрія). З введеного раніше визначення деформацій у точці: де l – абсолютна поздовжня деформація (видовження), l - довжина (базова довжина) стержня. Дослідним шляхом встановлений фундаментальний (фізичний) зв'язок зусиль і видовжень (Р. Гук) і в наступному, напруження і деформацій (Коші, Навьє) у вигляді: де Е – модуль пружності (фізична постійна матеріалу, що визначається експериментально). Підстановка останнього співвідношення - закону Гука в інтегральне вираження з урахуванням сталості деформацій та напружень дає : Нормальні напруження в поперечному перерізі прямо пропорційно величині поздовжнього зусилля і обернено пропорційно площі перерізу. Абсолютну деформацію (видовження) стержня також можна визначити через поздовжнє зусилля (отримана таким чином залежність називається законом Гука в розгорнутому вигляді): Формула для абсолютного видовження справедлива лише при постійній по довжині стержня поздовжній силі і незмінній площі поперечного перерізу! У разі змінної поздовжньої сили, наприклад, при врахуванні власної ваги вертикальних стержнів, та / або змінної площі необхідно використовувати інтегральний вираз: 11

Лекція 2 (продовження – 2. 5) n Коефіцієнт Пуассона - при розтягу стержня поряд з поздовжньою деформацією (видовженням), яке визначається законом Гука, виникає поперечна деформація (звуження поперечного перерізу), що виражається в зменшенні поперечних розмірів стержня. Відносні поперечні деформації обчислюються як де b, h - розміри поперечного перерізу. Експериментально встановлено, що існує лінійний зв'язок між поздовжньої і поперечної деформацією: де ν – коефіцієнт пропорційності, що називається коефіцієнтом Пуассона. Коефіцієнт Пуассона для певного матеріалу в межах пружних деформацій має постійне значення Матеріал і знаходиться в межах від 0 до 0, 5. За законом Гука, який визначає зв'язок нормальних напружень з поздовжніми деформаціями: тоді ν Сталь Мідь, бронза 0, 23 -0, 27 Бетон 0, 08 -0, 18 Деревина: вздовж волокон поперек волокон 0, 5 0, 02 Алюміній 0, 32 -0, 36 Резина, каучук Напруження на похилих площадках - при розтязі стержня в його поперечному перерізі виникають тільки нормальні напруження. Визначимо, які напруження виникають в перерізі, не перпендикулярному до осі стержня. n 1. Відкинемо праву частину та замінимо її дію головним вектором сил R : Аналіз отриманих співвідношень показує: Із рівнянь рівноваги, спроектувавши на вісь стержня R = F. 1. При α = 0 (похила площадка збігається з поперечним перерізом): 2. Розкладемо це внутрішнє зусилля на нормальну та дотичну до перерізу складову N и Q : дотичні напруження відсутні, а нормальні напруження максимальні. 0, 31 -0, 35 Чавун Як згадувалося раніше, в загальному випадку навантаження, по гранях виділеного елемента виникають нормальні і дотичні напруження. Останні, викликаючи деформації зсуву і не впливають на лінійні деформації, оскільки не змінюють довжин сторін елемента. Використовуючи принцип незалежності дії сил, справедливий для ізотропного і лінійно пружного матеріалу, можна записати узагальнений закон Гука, що враховує одночасну дію нормальних напружень по всіх гранях елемента: 0, 25 -0, 33 0, 47 -0, 5 N F 2. При α = 450 нормальні та 3. Підрахуємо : дотичні напруження максимальні, а нормальні напруження дотичні напруження на дорівнюють дотичним. похилому перерізу площею A =A / cos : 0 3. При раніше, (поздовжня площадка) нормальні і дотичні напруження перетворюються Тут, як і α = 90 : передбачається рівномірний З урахуванням того, що поздовжня сила N у поперечному перерізі в нуль (поздовжні волокна не розподіл напружень по перерізу. тиснуть один на одного і не зсуваються). дорівнює зовнішній розтягувальній силі F, відношення F / A = N / A є 4. На двох взаємно перпендикулярних площадках дотичні напруження нормальним напруженням в поперечному перерізі. Тоді отримуємо: рівні за абсолютною величиною. R F Q 12

Лекція 3 Випробування матеріалів на розтяг - стиск - При проектуванні конструкцій, машин і механізмів необхідно знати міцнісні і деформаційні властивості матеріалів. Їх визначають експериментально на спеціальних випробувальних машинах. З усіх властивостей (твердість, опірність ударним навантаженням, протидія високим або низьким температурам і т. п. ) основними є опір на розтягування і стиснення, що дають найбільшу і найважливішу інформацію про механічні властивості металів. n Випробування на розтяг – проводять на розривних або універсальних машинах, які мають спеціальні захвати для передачі зусилля. Використовуються стандартні зразки спеціальної форми (l 0 – довжина робочої частини, l 0/ a 0 = 5 – короткі, l 0/ a 0 = 10 – довгі): d n При випробуваннях на стиск застосовуються циліндричні зразки з відношенням висоти до діаметра h/d = 1, 5 – 3. Зразки встановлюються на опорну поверхню з використанням мастила для ослаблення впливу сил тертя. a 0 l 0 b 0 Всі машини обладнані пристроєм для автоматичного запису l 0 в певному масштабі діаграми-графіка залежності величини розтягуючої сили від подовження зразка. Сучасні машини комп'ютеризовані і мають засоби управління процесом навантаження по різним заданим програмам, виведення даних на екран і збереження їх у файлах для подальшої обробки: n Діаграми розтягу пластичних і крихких матеріалів – характерною діаграмою пластичних матеріалів є діаграма розтягування маловуглецевої сталі (< 0, 25% С): 1. У початковій стадії (OA, до Fпц) навантаження подовження зростає прямопропорційно величині навантаження F (на цій стадії справедливий закон Гука). E Fмакс K 2. Далі (AB, до Fпр) деформації починають рости трохи швидше і нелінійно, але залишаються малими і пружними Fпр С D FТ (деформації зникаючими після зняття навантаження). B Fпц Fк A 3. При подальшому навантаженні (BС, до Fт) криволінійна частина переходить в горизонтальну площадку CD, на якій деформації ростуть без збільшення навантаження (текучість). Зона BCD – зона загальної текучості. 4. При подальшому навантаженні (DE, до Fмакс) змінюється структура металу і матеріал O В точці K зразок раптово руйнується с різким ударним звуком, але без світлових ефектів. l знову може сприймати зростаюче навантаження (зміцнення) аж до максимального. 5. Далі (EK, до Fк) в найбільш слабкому місці виникає і розвивається локальне зменшення поперечного перерізу (шийка). Зона EK – зона місцевої текучості. 13

Лекція 3 (продовження – 3. 2) Характеристика міцності і пластичності – Розглянута вище діаграма розтягу зразка, що зв'язує навантаження з його видовженням не може безпосередньо характеризувати міцність і пластичність матеріалу, оскільки навантаження залежить від площі поперечного перерізу зразка, а видовження - від базової його довжини. Для отримання об'єктивних механічних характеристик матеріалу, що не залежать від перерізу і довжини зразка, необхідно перейти до напружень і відносних видовжень. Для цього навантаження ділиться на початкову або поточну площу поперечного перерізу зразка, а по осі абсцис відкладається відповідне відносне видовження для кожної їх характерних точок. n В результаті отримуємо діаграму напружень, подібну діаграмі розтягування : F E Fмакс Fпр С D B A Fпц FТ K Fк На цій діаграмі характерні точки визначають наступні механічні властивості матеріалу : 1. Межа пропорційності σпц – найбільше напруження, до якого існує пропорційна залежність між навантаженням і деформацією (для Ст3 σпц =195 -200 МПа). 2. Межа пружності σпр – найбільше напруження, при якому в матеріалі не виявляється ознак пластичної (залишкової) деформації (для Ст3 σпр =205 -210 МПа). l O 3. Межа текучості σт – найменше напруження, при якому зразок деформується без помітного збільшення розтягуючого навантаження (для Ст3 σт =220 -250 МПа). 4. Межа міцності або тимчасовий опір σв – напруження, що відповідає найбільшому навантаженню, що передбачає руйнування зразка (для Ст3 σв =370 -470 МПа). σ E σв σпр σпц O С D B A σТ σк σд 5. Дійсна межа міцності або дійсний опір розриву σд – напруження, що відповідає руйнуючій силі FK, обчислене для K 1 площі поперечного перерізу зразка в місці розриву A 1 (для Ст3 σд =900 -1000 МПа). Оскільки на ділянці EK утворюється шийка і площа K поперечного перерізу швидко зменшується, напруження збільшується (EK 1) при реєстрованому падінні зусилля. Механізм руйнування: в області шийки утворюються дрібні поздовжні тріщини, які потім зливаються в одну центральну тріщину, перпендикулярну осі розтягування, далі тріщина поширюється до поверхні шийки, розвертаючись приблизно на 450, і при виході на поверхню утворює конічну частину зламу. У результаті виходить поверхня зламу у вигляді "конуса" і "чашки". Стадія утворення конічної поверхні показує, що матеріал на вершині тріщини ε починає руйнуватися за механізмом ковзання (по майданчиках максимальних дотичних напружень), характерному для крихких матеріалів. 14

Лекція 3 (продовження – 3. 3) n n F FТ Fпц Діаграма стиску різних матеріалів – При стиску поводження матеріалу зразка відрізняється від його поведінки при розтягуванні. Діаграма маловуглецевої сталі – Початкова ділянка діаграми є прямолінійним (до точки A) і збігається з аналогічною ділянкою діаграми розтягування. Це свідчить про те, що модуль пружності у сталі можна приймати однаковим при розтягуванні і стисненні. Нелінійна ділянка до площадки текучості також збігається з подібною ділянкою на діаграмі розтягування. Значення межі пропорційності і межі текучості при розтягуванні і стисненні практично однакові. Площадка текучості при стисненні виражена дуже слабо і після неї крива йде все більш круто вгору внаслідок розвитку значних пластичних деформацій, що приводять до збільшення площі поперечного перерізу. Зразок сплющується B приймаючи бочкоподібну форму. На цьому випробування закінчують, тому що зразок зруйнувати A не вдасться, не вдається визначити і межу міцності. ■ Діаграма стиску чавуну – Початкова ділянка діаграми має майже лінійну залежність, на цій ділянці форма і розміри зразка змінюються незначно. При наближенні до максимального навантаження крива стає більш пологою і зразок приймає трохи бочкоподібну форму. При досягненні навантаженням найбільшого значення, з'являються тріщини під кутом приблизно 450 і настає руйнування по майданчиках з найбільшими дотичними напруженнями (крихке руйнування). Інші крихкі матеріали (камінь, бетон) мають подібну діаграму і такий характер руйнування. Крихкі матеріали працюють на стиск значно краще, ніж на розтяг, наприклад, межа міцності сірого чавуну на стиск 560 -900 МПа, а на розтяг - 120 -190 МПа. F l O Fmax l Fmax F A O B l ■ Діаграма стиску деревини – деревина – анізотропний матеріал. Опір при стисненні залежить від розташування волокон щодо направлення стискаючої сили. При стисненні вздовж волокон на ділянці OA деревина працює майже пружно, деформації ростуть пропорційно збільшенню стискаючої сили. Далі деформації починають рости швидше, ніж зусилля, внаслідок виникнення пластичних деформацій в окремих волокнах. Руйнування відбувається при максимальному навантаженні в результаті втрати місцевої стійкості ряду волокон, супроводжуваної зрушенням з утворенням поздовжніх тріщин. При стисненні деревини поперек волокон на ділянці OB деревина працює майже пружно, деформації ростуть пропорційно збільшенню стискаючої сили. далі деформації починають рости дуже швидко при малому збільшенні сили, внаслідок ущільнення (спресовування) окремих волокон. При наявності сучків і інших пороків (тріщин) зразок може зруйнуватися розколюванням. Руйнівне навантаження визначається умовно при досягненні деформації стиснення при якій висота зразка зменшується на третину вихідної висоти. 15

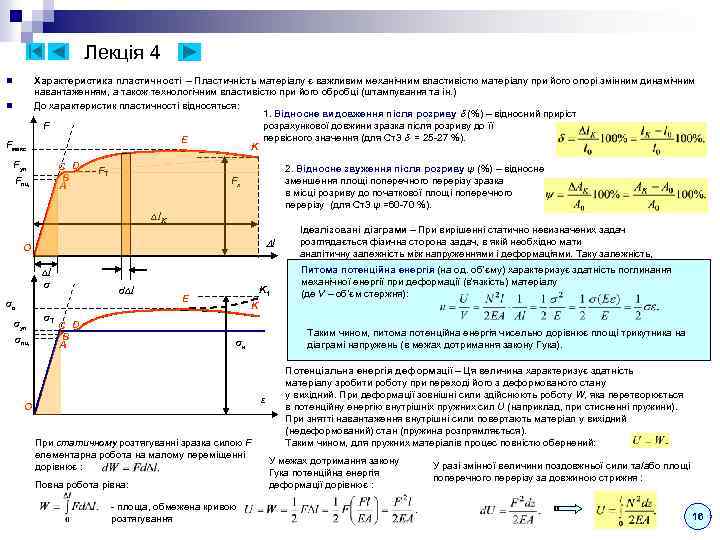Лекція 4 n n Fмакс Характеристика пластичності – Пластичність матеріалу є важливим механічним властивістю матеріалу при його опорі змінним динамічним навантаженням, а також технологічним властивістю при його обробці (штампування та ін. ) До характеристик пластичності відносяться: 1. Відносне видовження після розриву (%) – відносний приріст F розрахункової довжини зразка після розриву до її первісного значення (для Ст3 = 25 -27 %). E K Fуп С D B A Fпц FТ 2. Відносне звуження після розриву ψ (%) – відносне зменшення площі поперечного перерізу зразка в місці розриву до початкової площі поперечного перерізу (для Ст3 ψ =60 -70 %). Fк l K l O l σ d l σв σуп σпц σТ С D B A K 1 E K σи ε O При статичному розтягуванні зразка силою F елементарна робота на малому переміщенні дорівнює : Повна робота рівна: - площа, обмежена кривою розтягування Ідеалізовані діаграми – При вирішенні статично невизначених задач розглядається фізична сторона задач, в якій необхідно мати аналітичну залежність між напруженнями і деформаціями. Таку залежність, представлену отриманою експериментальнохарактеризує здатність поглинання Питома потенційна енергія (на од. об’єму) діаграмою напружень, складно отримати в енергії при деформації (в'язкість) матеріалу розрахунках. механічної аналітичному вигляді та використовувати в У (де V – об’єм стержня): зв’язку з цим, використовують спрощені (ідеалізовані) діаграми, що відображають основні закономірності. Наприклад, для пластичних матеріалів часто використовується діаграма Прандтля, що складається з двох прямолінійних ділянок. Як видно, діаграма Прандтля чином, питома потенційна енергія чисельно дорівнює площі трикутника на Таким поширює зону дії закону Гука до межі текучості, після чого передбачається (задається), напружень (в межах дотримання законуаж до руйнування. діаграмі що матеріал піддається далі текучості Гука). Потенціальна енергія деформації – Ця величина характеризує здатність матеріалу зробити роботу при переході його з деформованого стану у вихідний. При деформації зовнішні сили здійснюють роботу W, яка перетворюється в потенційну енергію внутрішніх пружних сил U (наприклад, при стисненні пружини). При знятті навантаження внутрішні сили повертають матеріал у вихідний (недеформований) стан (пружина розпрямляється). Таким чином, для пружних матеріалів процес повністю обернений: У межах дотримання закону Гука потенційна енергія деформації дорівнює : У разі змінної величини поздовжньої сили та/або площі поперечного перерізу за довжиною стрижня : 16

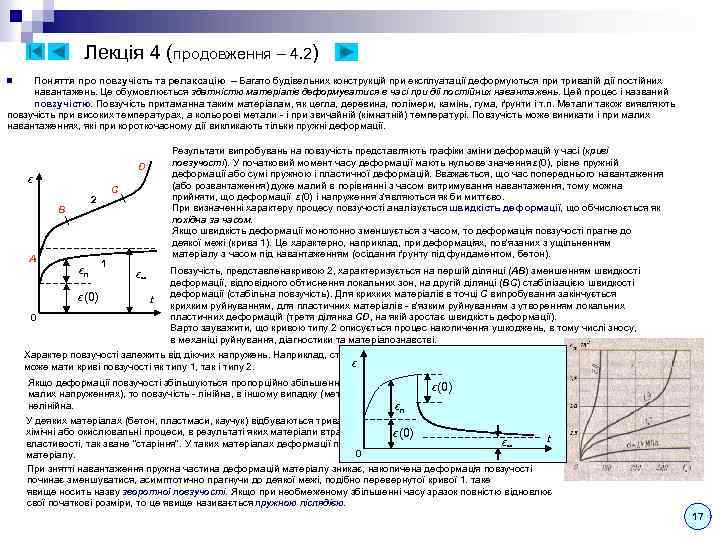Лекція 4 (продовження – 4. 2) Поняття про повзучість та релаксацію – Багато будівельних конструкцій при експлуатації деформуються при тривалій дії постійних навантажень. Це обумовлюється здатністю матеріалів деформуватися в часі при дії постійних навантажень. Цей процес і названий повзучістю. Повзучість притаманна таким матеріалам, як цегла, деревина, полімери, камінь, гума, ґрунти і т. п. Метали також виявляють повзучість при високих температурах, а кольорові метали - і при звичайній (кімнатній) температурі. Повзучість може виникати і при малих навантаженнях, які при короткочасному дії викликають тільки пружні деформації. n D ε εп ε(0) 0 C 2 B A Результати випробувань на повзучість представляють графіки зміни деформацій у часі (криві повзучості). У початковий момент часу деформації мають нульове значення ε(0), рівне пружній деформації або сумі пружною і пластичної деформацій. Вважається, що час попереднього навантаження (або розвантаження) дуже малий в порівнянні з часом витримування навантаження, тому можна прийняти, що деформації ε(0) і напруження з'являються як би миттєво. При визначенні характеру процесу повзучості аналізується швидкість деформації, що обчислюється як похідна за часом. Якщо швидкість деформації монотонно зменшується з часом, то деформація повзучості прагне до деякої межі (крива 1). Це характерно, наприклад, при деформаціях, пов'язаних з ущільненням матеріалу з часом під навантаженням (осідання ґрунту під фундаментом, бетон). 1 ε∞ t Повзучість, представленакривою 2, характеризується на першій ділянці (AB) зменшенням швидкості деформації, відповідного обтиснення локальних зон, на другій ділянці (BC) стабілізацією швидкості деформації (стабільна повзучість). Для крихких матеріалів в точці C випробування закінчується крихким руйнуванням, для пластичних матеріалів - в'язким руйнуванням з утворенням локальних пластичних деформацій (третя ділянка CD, на якій зростає швидкість деформації). Варто зауважити, що кривою типу 2 описується процес накопичення ушкоджень, в тому числі зносу, в механіці руйнування, діагностики та матеріалознавстві. Характер повзучості залежить від діючих напружень. Наприклад, сталь при різних рівнях напружень ε може мати криві повзучості як типу 1, так і типу 2. Якщо деформації повзучості збільшуються пропорційно збільшенню напружень (бетон, пластмаса при ε(0) малих напруженнях), то повзучість - лінійна, в іншому випадку (метал при високих температурах) нелінійна. εп У деяких матеріалах (бетон, пластмаси, каучук) відбуваються тривалі, повільно протікаючі хімічні або окислювальні процеси, в результаті яких матеріали втрачають свої ε(0) первинні ε∞ властивості, так зване "старіння". У таких матеріалах деформації повзучості звичайно залежать від "віку" 0 матеріалу. t При знятті навантаження пружна частина деформацій матеріалу зникає, накопичена деформація повзучості починає зменшуватися, асимптотично прагнучи до деякої межі, подібно перевернутої кривої 1. таке явище носить назву зворотної повзучості. Якщо при необмеженому збільшенні часу зразок повністю відновлює свої початкові розміри, то це явище називається пружною післядією. 17

Лекція 4 (продовження – 4. 3) n Релаксація напружень – Якщо зразок витримується протягом деякого тривалого часу в стані, при якому деформація залишається постійною, то напруження в матеріалі, що мали в початковий момент значення σ(0), понижуються асимптотично до деякого значення. Явище повільного зменшення напружень у зразку при постійній деформації називається релаксацією. Таким чином, явище релаксації в деякій мірі зворотне повзучості, але природа цих двох явищ одна енергія теплових пружних коливань атомів додається до енергії, яка забезпечується зовнішніми силами, що викликають деформацію. При вільній деформації під дією прикладених сил відбувається додатковий рух дислокацій (дислокаціїдефекти кристалічної решітки) і деформація зростає. Оскільки при звичайній температурі ця енергія незначна, то повзучість (приріст деформацій) відбувається в цьому випадку повільно. При постійній деформації надходження додаткової енергії теплових коливань атомів призводить до перерозподілу дислокацій з частковим відновленням регулярності кристалічної решітки. При цьому енергія деформації зменшується, що призводить до зменшення напружень, якщо деформація залишається постійною. σ σ(0) 0 t σ∞ 18

Лекція 5 n n Основні відомості про розрахунок конструкцій. Методи допустимих напружень та граничних станів – Основним завданням розрахунку конструкції є забезпечення її міцності в умовах експлуатації. Міцність конструкції, виконаної з крихких матеріалів, вважається забезпеченою, якщо у всіх поперечних перерізах фактичні напруження менше межі міцності матеріалу. Величини навантаження, напруження в конструкції та механічні характеристики матеріалу не можуть бути встановлені зовсім точно через те, що мають місце такі чинники, як випадковий характер навантаження, наближеність розрахунку, похибка випробувань, розкид механічних властивостей реальних матеріалів і т. д. Тому необхідно, щоб найбільші напруження, отримані в результаті розрахунку (розрахункові напруження) не перевищували деякої величини, меншої межі міцності. Ця величина називається допустимими напруженнями і встановлюється діленням межі міцності на коефіцієнт, більший одиниці, названий коефіцієнтом запасу міцності. Відповідно до цього умова міцності : де - найбільші розрахункові розтягуючі і стискаючі напруження в конструкції; - допустимі напруження при розтягуванні і стисненні відповідно. Допустимі напруження пов'язані з межею міцності на розтягування і стиснення відношеннями : де n. В – нормативний (необхідний) коефіцієнт запасу міцності по відношенню до межі міцності, який визначається в залежності від класу конструкції (капітальна, тимчасова і т. п. ), від передбачуваного (заданого) терміну служби, від характеру навантаження (статична, динамічна і т. п. ), від умов роботи конструкції, від якості виготовлення матеріалів та інших факторів. Величина n. В в більшості випадків приймається в діапазоні від 2, 5 до 5. Для конструкцій з пластичних матеріалів, що мають однакові межі міцності на розтягування і стиснення, умова міцності : Допустимі напруження : де max – найбільші за абсолютною величиною стискаючі або розтягуючі напруження в конструкції. де n. Т – нормативний (необхідний) коефіцієнт запасу міцності по відношенню до межі текучості (n. Т = 1, 5 – 2, 5). Отже, умова міцності за методом допустимих напружень при перевірці напружень при розтягуванні-стисненні стрижнів має вигляд : При підборі перерізу, прийняті розміри перерізу повинні забезпечувати нерівність, що випливає з умови міцності : При визначенні вантажопід’ємності обчислюється допустима поздовжня сила в найбільш навантаженому стержні : За отриманою допустимої силі визначається далі величина допустимого навантаження [F]. Умова міцності приймає вид : 19

Лекція 5 (продовження – 5. 2) n Визначення граничних навантажень в статично невизначених системах з ідеального пружно-пластичного матеріалу –Раніше на лекціях було розглянуто розрахунок статично невизначених стержневих систем при їх роботі в пружній стадії. Метою розрахунку було визначення зусиль, що виникають в стержнях, знання яких дозволяє підібрати переріз. Оскільки в пружному розрахунку співвідношення жорсткостей (а, отже, площ) задається заздалегідь, то завжди виявляється, що в деяких стержнях, або ділянках стержнів змінного перерізу, напруження будуть менше граничних (або допустимих), ніж в стержні (або на ділянці), в якому напруження максимальні і які були використані при складанні умови міцності та визначення необхідної площі поперечного перерізу. Все це становить основу методу розрахунку по допустимих напруженнях. Статично невизначені системи мають "зайві" зв'язки і вихід одного з них з ладу при збільшенні навантаження не означає, що система більше не може залишатися в рівновазі. Таким чином, граничним станом для статично невизначених систем не є виникнення напружень більше розрахункових (допустимих) в самому навантаженому стержні (або на ділянці ступінчастого стержня). n Метод руйнуючих навантажень – Оскільки при досягненні в одному із стержнів напружень більше розрахункових (границі текучості) несуча здатність статичної системи не вичерпується, то слід прийняти за небезпечний стан такий, при якому у всіх стержнях, що Тепер при Fгран = [F]n виникає переміщень) виникають напруження, рівні межі текучості. забезпечують незмінність системи (рівновагу при відсутності будь-яких текучість ще й на третій ділянці і система вже не може сприймати навантаження (друга ділянка буде Для такого стану система перестає бути статично невизначеної, так як тепер відомі зусилля в цих стержнях. Вони дорівнюють добутку переміщуватися внаслідок текучості на першій та третій ділянках). поперечної площі перерізу на напруження, рівні межі текучості. Вантажопід’ємність, визначена по методу (діаграми Прандтля), яка Все це справедливо при використанні ідеалізованої діаграми розтягування-стисненняруйнівних навантажень, не враховує зміцнення більше, матеріалу після проходження площадки текучості. ніж визначена по методу допустимих напружень на (0, 3750, 25)/0, 25)100%=50%, тобто в півтора рази. Таким чином, граничне навантаження може бути визначене з умов рівноваги. Очевидно, що таке навантаження не може бути допущене щоб уникнути руйнування системи. Тому його величину ділять на коефіцієнт запасу n, подібно до того, як граничні напруження при пружному розрахунку ділилися на цей коефіцієнт по відношенню до межі міцності або межі текучості. Умова міцності за методом руйнуючих навантажень при розтягуванні-стисненні стрижнів статично невизначеної системи має вигляд : де n У випадку дії декількох сил передбачається, що сили одночасно збільшуються пропорційно деякого параметру. Тоді знаходиться граничне значення цього параметра, що характеризує граничне навантаження. Приклад – Стержень ступінчастого перерізу знаходиться під дією сили F. Ця статично невизначена задача була розглянута і вирішена раніше на лекціях. Отримане пружне рішення : max = 0. 375 F/A. Необхідно визначити z B RB RA A вантажопідйомність за методом допустимих напружень і методу руйнуючих навантажень. F Умова міцності по допустимим напруженням: a a a Тоді при Fгран = Fn виникає текучість на першій ділянці, але система може ще сприймати навантаження, тому що на інших ділянках напруження менше Т. 0, 375 F/A + 0, 125 F/A - 0, 25 F/A - σ умова міцності по руйнуючим навантаженням: 20

Лекція 5 (продовження – 5. 3) Три види розрахунків на міцність при розтягу та стиску Умова міцності при розтязі та стиску 1. Перевірочний розрахунок (перевірка умови міцності): відоме навантаження (поздовжня сила) - N; відомі розміри перерізу (площа поперечного перерізу) – А; відомий матеріал (допустимі напруження) - [σ]. 2. Підбір розмірів поперечного перерізу: відоме навантаження (поздовжня сила) - N; відомий матеріал (допустимі напруження) - [σ]; відомий тип площі поперечного перерізу. 3. Визначення найбільшого допустимого навантаження: відомі розміри перерізу (площа поперечного перерізу) – А; відомий матеріал (допустимі напруження) - [σ]. ПРИКЛАД: Умова міцності: , , . 21

Лекція 6 n Визначення переміщень при розтязі-стиску. Розглянемо стержень, навантажений розтягуючою силою F. Виділимо на відстані z ділянку довжиною dz. Видовження цієї ділянки dz рівне переміщенню другої її межі щодо першої dw. Деформація на цій ділянці визначається виразом, w(z)+dw і представляє собою диференціальне рівняння: F z Розділимо змінні і зведемо рішення цього рівняння до інтегрування лівої і правої частин: z dz Підставимо межі і вираз для деформації, що слідує із закону Гука : Тут w 0 – переміщення лівої межі аналізованої ділянки на відстані z, EА- жорсткість стержня при розтязі-стиску, N - поздовжня сила. У разі постійності поздовжньої сили і площі поперечного перерізу маємо: Звідси, як окремий випадок, отримуємо вираз для абсолютного подовження стержня (w 0 = 0, z = l): Загальна формула обчислення переміщень показує, що переміщення обчислюються наростаючим підсумком, тобто до переміщення, обчислюваному Таким чином, врахування рівномірно розподіленого поздовжнього навантаження (власної ваги) може бути на даній ділянці [z 0, z] (другий доданок), додається переміщення перерізу, відповідного лівій межі, іділянці або використанням виконано безпосереднім інтегруванням по розглядуваній представляє переміщення всієї ділянки, як жорсткого цілого (твердого тіла). Якщо на кожній з ділянок поздовжнє при постійній поздовжній силі, виразу, подібного абсолютному видовження стержня зусилля і площа поперечного перерізу постійні, то визначення переміщення будь-якого перерізу або кінця стержня зводиться до результатпідсумовування видовжень кожного в якому сила зменшена удвічі! (див. простого визначення переміщення кінця стержня). з ділянок від нерухомого перерізу до розглянутого. Наприклад, другий результат власною вагою (довжина стержня об'ємна вага матеріалу стержня ). n Врахування власної ваги. Розглянемо стержень, навантажений (переміщення перерізу посерединіl, довжини стержня) може бути отриманий, як сума переміщень розглянутого перерізу стержня від дії власної ваги верхньої Поздовжнє зусилля від власної ваги в довільному перерізі на відстані z дорівнює вазі нижчерозташованої частини стержня частини, враховуваного як розподілене навантаження, і переміщення його від ваги нижньої частини, і лінійно залежить від координати. Епюри поздовжньої сили і нормальних напружень мають вигляд трикутників: діючого на верхню частину як зовнішня сила: Переміщення будь-якого перерізу на відстані z має квадратну залежність від координати: σ N w + z + Визначимо переміщення кінця стержня і перерізу на відстані половини довжини : + Тут G - вага стержня. 22 z

Лекція 6 (продовження – 6. 2) Брусом рівного опору називається брус, у якому напруження за довжиною не змінюються і, як правило, дорівнюють допустимим напруженням. Умова рівноваги знизу ділянки dx (переріз 1): Умова рівноваги зверху ділянки dx (переріз 2): Віднявши ці два рівняння, отримаємо: або Проінтегруємо ліву і праву частини отриманої рівності: Знайдемо сталу інтегрування С: При х = 0, Із знайденою сталою інтегрування С: Звідки - формула підбору перерізу брусу рівного опору при розтязі або стиску. Для спрощення розрахунку та виготовлення, брус рівного опору замінюють ступінчастим брусом. 23

Лекція 7 Геометричні характеристики поперечних перерізів. Величина нормальних напружень у поперечному перерізі розтягнутого (стиснутого) стержня залежить від площі цього перерізу. Таким чином, площа поперечного перерізу є геометричною характеристикою, що визначає напруження при розтягуванні (стисканні). У випадку інших видів напружено-деформованого стану (згин, кручення), напруження залежать не від площі, а від деяких інших геометричних характеристик поперечного перерізу. Ієрархія геометричних характеристик встановлюється видом підінтегрального виразу і представляється наступним чином: Площа поперечного перерізу: n y. C y n. Статичні dy y d. A n. Статичні dx x моменти використовуються при визначенні положення центру ваги: x. C Визначення координат центру ваги. Методи визначення положення центра ваги плоских фігур розглядалися в курсі теоретичної механіки, наприклад, метод розбиття на декілька елементарних елементів: x x. C C y. C O моменти площі поперечного перерізу: Тут xi, yi - координати центрів ваги простих фігур, для яких вони відомі або легко знаходяться. Нагадаємо процедуру визначення положення центра ваги: 1. вибрати довільну (початкову) систему координат x, y. 2. розбити задану фігуру на більш прості фігури. 3. обчислити статичні моменти і використовувати формули координат центру ваги. Осі, що проходять через центр ваги фігури, називаються центральними. Можна показати, що відносно центральних осей, статичні моменти площі перетворюються в нуль. Приклад 1 - Визначити положення центру ваги куткового поперечного перерізу. 1. Вибираємо систему координат x, y з початком в нижньому лівому куті перерізу. 4 2. Розбиваємо фігуру на два прямокутники, обчислюємо площі і координати центрів ваги кожного: 1 C 12 2 4 O 3. Обчислюємо статичні моменти і координати центру ваги всього перерізу: 20 24

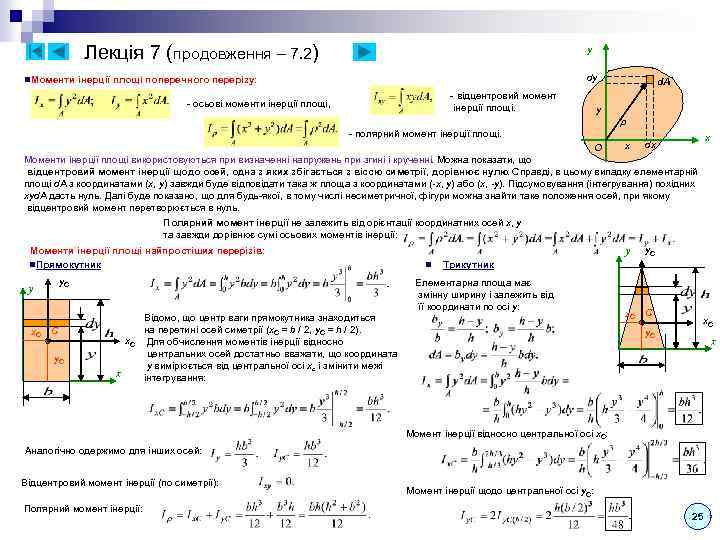Лекція 7 (продовження – 7. 2) n. Моменти y dy інерції площі поперечного перерізу: - відцентровий момент інерції площі. - осьові моменти інерції площі, y d. A - полярний момент інерції площі. O x x dx Моменти інерції площі використовуються при визначенні напружень при згині і крученні. Можна показати, що відцентровий момент інерції щодо осей, одна з яких збігається з віссю симетрії, дорівнює нулю. Справді, в цьому випадку елементарній площі d. A з координатами (x, y) завжди буде відповідати така ж площа з координатами (-x, y) або (x, -y). Підсумовування (інтегрування) похідних xyd. A дасть нуль. Далі буде показано, що для будь-якої, в тому числі несиметричної, фігури можна знайти таке положення осей, при якому відцентровий момент перетворюється в нуль. Полярний момент інерції не залежить від орієнтації координатних осей х, у та завжди дорівнює сумі осьових моментів інерції: Моменти інерції площі найпростіших перерізів: n. Прямокутник y. C y x. C C x. C y. C x Відомо, що центр ваги прямокутника знаходиться на перетині осей симетрії (x. C = b / 2, y. C = h / 2). Для обчислення моментів інерції відносно центральних осей достатньо вважати, що координата y вимірюється від центральної осі xc і змінити межі інтегрування: у n y. C Трикутник Елементарна площа має змінну ширину і залежить від її координати по осі y: x. C C y. C x Момент інерції відносно центральної осі x. C: Аналогічно одержимо для інших осей: Відцентровий момент інерції (по симетрії): Полярний момент інерції: Момент інерції щодо центральної осі y. C: 25

Лекція 7 (продовження – 7. 3) n. Круглий переріз: Обчислимо спочатку полярний момент інерції: y d R Моменти інерції щодо центральних осей з x урахуванням симетрії: У техніці часто використовують наближені значення (похибка менше 2%): n. Кільцевий y переріз: Достатньо змінити межі інтегрування: d R Моменти інерції площі складених перерізів обчислюються, так само як і при обчисленні координат центру ваги, методом розбиття на прості фігури, для яких відомі або легко обчислюються координати центрів ваги і моменти інерції. Наприклад, момент інерції кільцевого перерізу може бути обчислений як різниця моментів інерції круглого суцільного перерізу радіусу R і такого ж перерізу, але радіуса r. Зауважимо, що при додаванні моментів інерції по кожній з координатних осей для кожної з фігур моменти інерції повинні обчислюватися відносно осей, які є загальними для розглянутого перерізу і всіх складових фігур. Звідси випливає необхідність оперувати формулами, що дозволяють переходити від одних до інших осей. n n. Залежність між моментами інерції при паралельному переносі осей d. A x 1 x Моменти інерції щодо центральних осей з урахуванням симетрії: r y y 1 O y Для тонкостінного кільця (t < 0, 075 R) можна наближено вважати, що = Rср = const по його товщині A = 2 Rсрt: t R R O 1 b y x a x 1 x Аналогічно для осі y 1: x У техніці іноді використовують наближені значення у вигляді: Формули спрощуються, якщо вихідні осі є центральними, т. я. Sx. C = Sy. C = 0: 26

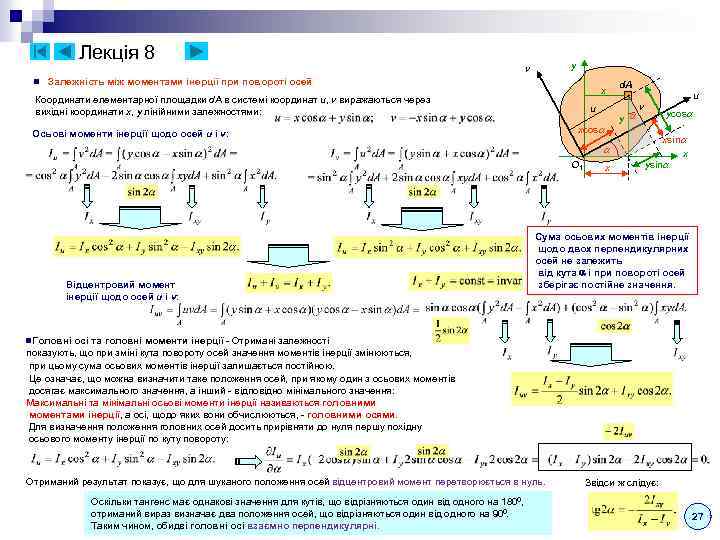Лекція 8 n y v Залежність між моментами інерції при повороті осей x Координати елементарної площадки d. A в системі координат u, v виражаються через вихідні координати x, y лінійними залежностями: u y xcos Осьові моменти інерції щодо осей u і v: O 1 Відцентровий момент інерції щодо осей u і v: d. A x u v ycos xsin x ysin Сума осьових моментів інерції щодо двох перпендикулярних осей не залежить від кута і при повороті осей зберігає постійне значення. n. Головні осі та головні моменти інерції - Отримані залежності показують, що при зміні кута повороту осей значення моментів інерції змінюються, при цьому сума осьових моментів інерції залишається постійною. Це означає, що можна визначити таке положення осей, при якому один з осьових моментів досягає максимального значення, а інший - відповідно мінімального значення: Максимальні та мінімальні осьові моменти інерції називаються головними моментами інерції, а осі, щодо яких вони обчислюються, - головними осями. Для визначення положення головних осей досить прирівняти до нуля першу похідну осьового моменту інерції по куту повороту: Отриманий результат показує, що для шуканого положення осей відцентровий момент перетворюється в нуль. Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз визначає два положення осей, що відрізняються один від одного на 900. Таким чином, обидві головні осі взаємно перпендикулярні. Звідси ж слідує: 27

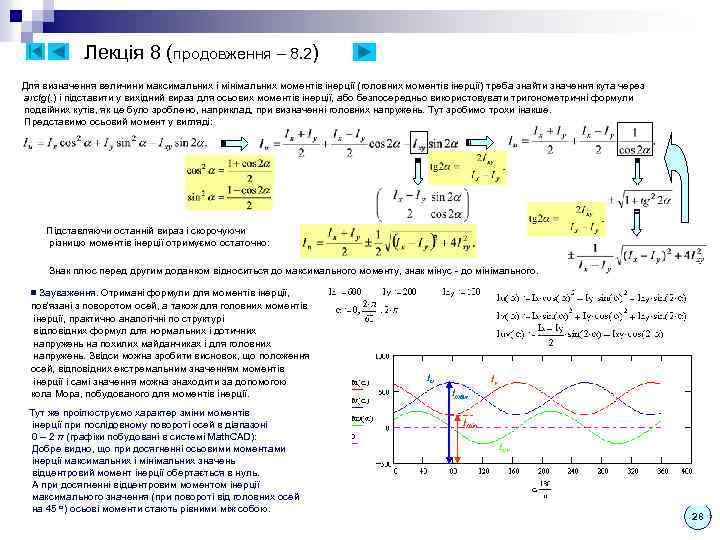Лекція 8 (продовження – 8. 2) Для визначення величини максимальних і мінімальних моментів інерції (головних моментів інерції) треба знайти значення кута через arctg(. ) і підставити у вихідний вираз для осьових моментів інерції, або безпосередньо використовувати тригонометричні формули подвійних кутів, як це було зроблено, наприклад, при визначенні головних напружень. Тут зробимо трохи інакше. Представимо осьовий момент у вигляді: Підставляючи останній вираз і скорочуючи різницю моментів інерції отримуємо остаточно: Знак плюс перед другим доданком відноситься до максимального моменту, знак мінус - до мінімального. Зауваження. Отримані формули для моментів інерції, пов'язані з поворотом осей, а також для головних моментів інерції, практично аналогічні по структурі відповідних формул для нормальних і дотичних напружень на похилих майданчиках і для головних напружень. Звідси можна зробити висновок, що положення осей, відповідних екстремальним значенням моментів інерції і самі значення можна знаходити за допомогою кола Мора, побудованого для моментів інерції. n Тут же проілюструємо характер зміни моментів інерції при послідовному повороті осей в діапазоні 0 – 2 π (графіки побудовані в системі Math. CAD): Добре видно, що при досягненні осьовими моментами інерції максимальних і мінімальних значень відцентровий момент інерції обертається в нуль. А при досягненні відцентровим моментом інерції максимального значення (при повороті від головних осей на 45 о ) осьові моменти стають рівними між собою. Iu Iv Imax Imin Iuv 28

Лекція 8 (продовження – 8. 3) n Радіус інерції - є величина, що зв'язує момент інерції з площею поперечного перерізу і визначається з рівності: Радіус інерції являє собою відстань від розглянутої осі до тієї точки, в якій умовно можна зосередити всю площу поперечного перерізу. Ця величина характеризує наскільки добре "розвинений" переріз, як далеко знаходяться від осі окремі області перерізу, що в свою чергу характеризує економічність перерізу при згині і стиску із згином. Радіусом інерції зручно користуватися при оцінці гнучкості стиснутих стержнів. Звичайно для цього радіуси інерції попередньо обчислюються для типових і прокатних перерізів за формулами: Радіуси інерції, відповідні головним осях, називаються головними радіусами інерції і визначаються за формулами: Обчислення моментів інерції складних фігур - виконується в наступному порядку: Переріз розбивається на частини, для яких відомі координати центрів ваги і моменти інерції або легко знаходяться. Вибираються початкові осі, щодо яких обчислюються координати центру ваги перерізу. Обчислюються координати центра ваги перерізу. Проводяться центральні осі (що проходять через центр ваги перерізу), щодо яких обчислюються моменти інерції. Обчислюються осьові і відцентрові моменти інерції всього перерізу щодо центральних осей. Обчислюються головні центральні моменти і визначається положення головних осей. n 1. 2. 3. 4. 5. 6. Приклад 1 - Визначити головні центральні моменти інерції і положення головних осей кутикового поперечного перерізу. t 2 1 C h 1 2 t O a 29

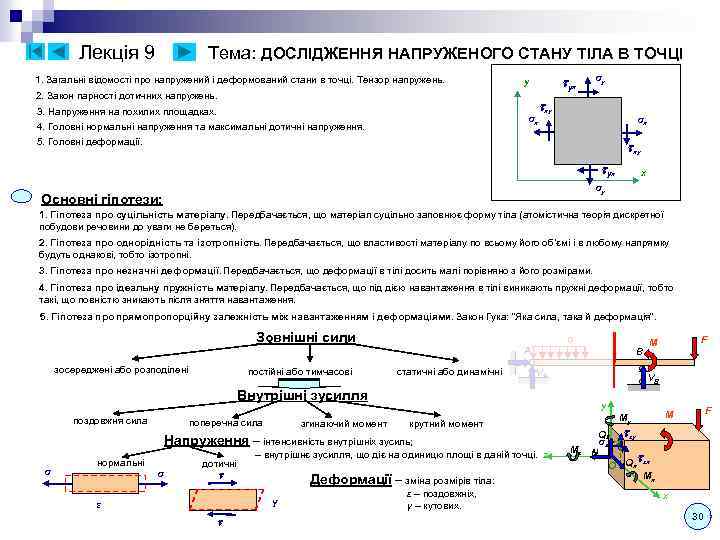Лекція 9 Тема: ДОСЛІДЖЕННЯ НАПРУЖЕНОГО СТАНУ ТІЛА В ТОЧЦІ 1. Загальні відомості про напружений і деформований стани в точці. Тензор напружень. yx у 2. Закон парності дотичних напружень. 3. Напруження на похилих площадках. σx 4. Головні нормальні напруження та максимальні дотичні напруження. σy xy σx 5. Головні деформації. xy yx x σy Основні гіпотези: 1. Гіпотеза про суцільність матеріалу. Передбачається, що матеріал суцільно заповнює форму тіла (атомістична теорія дискретної побудови речовини до уваги не береться). 2. Гіпотеза про однорідність та ізотропність. Передбачається, що властивості матеріалу по всьому його об’ємі і в любому напрямку будуть однакові, тобто ізотропні. 3. Гіпотеза про незначні деформації. Передбачається, що деформації в тілі досить малі порівняно з його розмірами. 4. Гіпотеза про ідеальну пружність матеріалу. Передбачається, що під дією навантаження в тілі виникають пружні деформації, тобто такі, що повністю зникають після зняття навантаження. 5. Гіпотеза про прямопропорційну залежність між навантаженням і деформаціями. Закон Гука: “Яка сила, така й деформація”. Зовнішні сили q A зосереджені або розподілені постійні або тимчасові статичні або динамічні B VA VB Внутрішні зусилля поздовжня сила поперечна сила згинаючий момент y σ нормальні σ дотичні – внутрішнє зусилля, що діє на одиницю площі в даній точці. z Деформації – зміна розмірів тіла: γ ε My крутний момент Напруження – інтенсивність внутрішніх зусиль; ε – поздовжніх, γ – кутових. F M Mz N F M Qу zy σz x O Qx zx Mx x 30

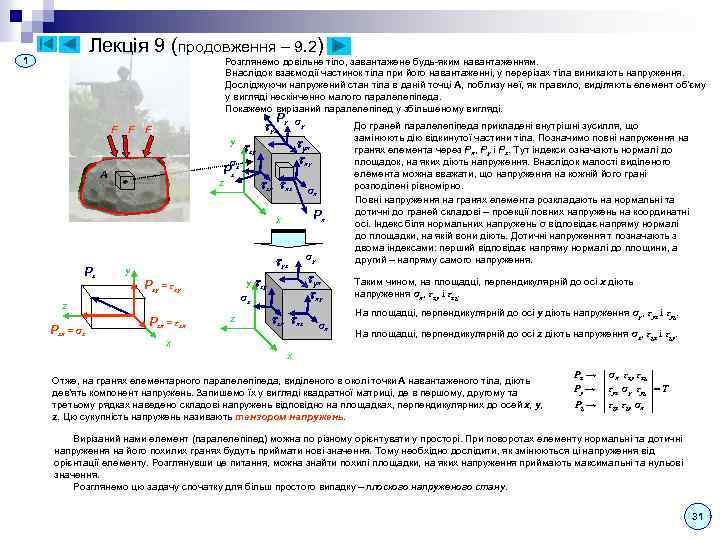Лекція 9 (продовження – 9. 2) 1 F F Розглянемо довільне тіло, завантажене будь-яким навантаженням. Внаслідок взаємодії частинок тіла при його навантаженні, у перерізах тіла виникають напруження. Досліджуючи напружений стан тіла в даній точці А, поблизу неї, як правило, виділяють елемент об’єму у вигляді нескінченно малого паралелепіпеда. Покажемо вирізаний паралелепіпед у збільшеному вигляді. Р До граней паралелепіпеда прикладені внутрішні зусилля, що у σy F yz y zx xz z yz y y σz Рzу = τzу z Рzх = σz Рzх = τzх z Таким чином, на площадці, перпендикулярній до осі х діють напруження σх, τху і τхz. σx Рх x Рz σy yx xy σ Рz z А замінюють дію відкинутої частини тіла. Позначимо повні напруження на гранях елемента через Рх, Ру і Рz. Тут індекси означають нормалі до площадок, на яких діють напруження. Внаслідок малості виділеного елемента можна вважати, що напруження на кожній його грані розподілені рівномірно. Повні напруження на гранях елемента розкладають на нормальні та дотичні до граней складові – проекції повних напружень на координатні осі. Індекс біля нормальних напружень σ відповідає напряму нормалі до площадки, на якій вони діють. Дотичні напруження τ позначають з двома індексами: перший відповідає напряму нормалі до площини, а другий – напряму самого напруження. yx xy zy zx xz x σx На площадці, перпендикулярній до осі у діють напруження σy, τуx і τyz. На площадці, перпендикулярній до осі z діють напруження σz, τzx і τzy. x Отже, на гранях елементарного паралелепіпеда, виділеного в околі точки А навантаженого тіла, діють дев’ять компонент напружень. Запишемо їх у вигляді квадратної матриці, де в першому, другому та третьому рядках наведено складові напружень відповідно на площадках, перпендикулярних до осей x, y, z. Цю сукупність напружень називають тензором напружень. Px → Py → σх τху τхz τyx σy τyz = T Pz → τzх τzy σх Вирізаний нами елемент (паралелепіпед) можна по різному орієнтувати у просторі. При поворотах елементу нормальні та дотичні напруження на його похилих гранях будуть приймати нові значення. Тому необхідно дослідити, як змінюються ці напруження від орієнтації елементу. Розглянувши це питання, можна знайти похилі площадки, на яких напруження приймають максимальні та нульові значення. Розглянемо цю задачу спочатку для більш простого випадку – плоского напруженого стану. 31

2 n Лекція 9 (продовження – 9. 3) yz Плоский напружений стан – такий стан, при якому дві паралельні грані елементу вільні від напружень, тобто на них відсутні і нормальні, і дотичні напруження. Такий стан виникає в тонких пластинках, поверхні яких вільні від навантаження, на ненавантаженій поверхні тіл, при згині балок, крученні валів тощо. σx zy yx xy zx xz yx z Розглянемо нескінченно малий об’єм у вигляді паралелепіпеда навколо досліджуваної точки А. Нехай, наприклад, по площадці, перпендикулярній вісі z напруження відсутні. y σz σy x Нижче буде показано, що в цьому випадку напруження zx і zу також будуть відсутні. σx σy σy yx у Тепер об’ємний елемент можна представити у вигляді його проекції на площину ху. На рисунку показані додатні напрямки напружень, що відповідають наступним правилам: 1. додатні нормальні напруження направлені в сторону зовнішньої нормалі відповідної грані, тобто вони викликають деформації розтягу елементу; 2. додатні дотичні напруження повертають елемент по годинниковій стрілці (назустріч осі z). σx xy У загальному випадку, напруження в деформованому стані змінюються від точки до точки, тобто являються функціями координат. Тут при розгляді нескінченно малого елементу можна вважати, що напружений стан однорідний і напруження по кожній грані постійні і на паралельних гранях елементу рівні між собою. Виділений елемент повинен знаходиться у рівновазі та задовольняти рівнянням рівноваги для будь-якої плоскої системи сил – рівнодіючої по кожній із граней прикладених зусиль: - суми проекцій на координатні осі тотожно рівні нулю. Складемо суму моментів всіх сил відносно лівого нижнього кута (точки А): σx dy A dx xy yx x σy Отриманий закон парності дотичних напружень: Дотичні напруження на двох взаємно перпендикулярних площадках рівні один одному по величині та протилежні по знаку. Таким чином, показані напрямки дотичних напружень на рисунку, присвячених правилам знаків, не відповідають стану рівноваги елементу. Можливі правильні напрямки дотичних напружень будуть наступні: yx<0 yx>0 xy<0 xy>0 yx xy yx 32

3 n Лекція 10 Напруження на похилих площадках. Для визначення напружень на похилій площадці, зовнішня нормаль якої повернута на кут α до осі х, використовуємо метод перерізів: 1. проведемо похилий переріз; 2. відкинемо праву частину; 3. замінимо відкинуту частину внутрішніми зусиллями, які представимо у вигляді компонент напружень – нормального та дотичного (на рисунку всі напруження показані додатними); y yx xy z 4. складемо рівняння рівноваги для рівнодіючих напружень в проекціях на нормаль n до похилого перерізу та вісь, дотичну t до перерізу: yx у σy dy σx xy n σ σx x dz σy t yx dy. tg σx xy x σy Після ділення рівнянь на dydz, множення на cos , підстановки закону парності дотичних напружень та переносу у праву частину відомих напружень, отримаємо: Або використовуючи відомі тригонометричні формули подвійного кута: Отримані формули для визначення напружень на будь-яких площадках, що проходять через дану точку, якщо відомі напруження x, y і yx = - xy. Визначимо, які будуть напруження на площадці, перпендикулярній до розглядуваної похилої площадки: Із порівняння виразів для дотичних напружень знову можна отримати закон парності дотичних напружень: +900 = - . Додаючи вирази для нормальних напружень, отримуємо закон незмінності суми нормальних напружень на будь-яких взаємно-перпендикулярних площадках: Із незмінності суми нормальних напружень слідує, що при повороті цих площадок приріст (зміна) нормальних напружень однакові і протилежні за знаком: Відповідно, якщо на одній із площадок нормальні напруження досягають максимуму, то на другій площадці вони перетворюються в мінімальні. 33

4 Лекція 10 (продовження – 10. 2) Головні напруження. При розрахунку конструкцій на міцність необхідно визначати величину максимальних напружень. Максимальні та мінімальні нормальні напруження називаються головними напруженнями, а площадки, на яких вони діють – головними площадками. Для визначення положення головних площадок достатньо прирівняти до нуля першу похідну нормальних напружень по куту нахилу площадок: n Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз визначає дві площадки, що відрізняються один від одного на 900. Таким чином, обидві головні площадки взаємно перпендикулярні. Зауважимо, що похідна нормальних напружень на похилій площадці по куту нахилу площадки рівна подвоєній величині дотичних напружень на цій площадці. Таким чином, на головних площадках дотичні напруження дорівнюють нулю. Для визначення величини максимальних і мінімальних нормальних напружень необхідно знайти значення кута через arctg(…) і підставити у вихідний вираз для нормальних напружень. Але простіше безпосередньо використати наступні тригонометричні формули: Підстановка цих тригонометричних функцій у формулу нормальних напружень дає для однієї із головних площадок: Оскільки кут для другої головної площадки відрізняється від першої на 900, то синус і косинус подвійного кута змінює знак на протилежний, що приводить до зміни знаку другого доданку: Таким чином, по двом головним площадкам діють головні напруження: 34

Лекція 10 (продовження – 10. 3) n Максимальні дотичні напруження. Існують площадки, на яких дотичні напруження досягають максимальних значень. Для визначення їх положення достатньо прирівняти до нуля першу похідну дотичних напружень по куту нахилу площадок: Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз визначає дві площадки, що відрізняються одна від одного на 900. Таким чином, обидві площадки взаємно перпендикулярні. Проте на цих площадках у загальному випадку нормальні напруження перетворюються в нуль. Площадки, на яких дотичні напруження максимальні, називаються площадками зсуву. Визначимо кут між площадкою зсуву і головною площадкою. Порівняємо формули для кутів нахилу головних площадок та площадок зсуву: Оскільки праві частини обернені один одному, то Таким чином, площадки зсуву повернуті відносно головних площадок на кут 450. Для визначення величини максимальних дотичних напружень необхідно знайти значення кута через arctg(…) і підставити у вихідний вираз для дотичних напружень, але простіше прийняти у якості вихідного стану головні площадки і перейти до площадок зсуву: При підстановці кута 1350 або -450 (друга площадка зсуву) отримаємо той же результат, але із оберненим знаком. Таким чином, знову дотримується закон парності дотичних напружень і в загальному випадку можна записати: Підставимо вирази для головних напружень: 5 n Поняття про круг Мора для напружень. Існує графічний спосіб визначення положень головних площадок та напружень, а також напружень на будь-яких інших площадках. Спосіб базується на залежності між нормальними і дотичними напруженнями, що описується рівнянням ІІ порядку, а саме рівнянням круга. Отже, отримане рівняння ІІ порядку: Підведемо до квадрату обидві частини рівнянь для напружень і Порівняємо його з рівнянням круга: додамо: =0 =1 =1 35

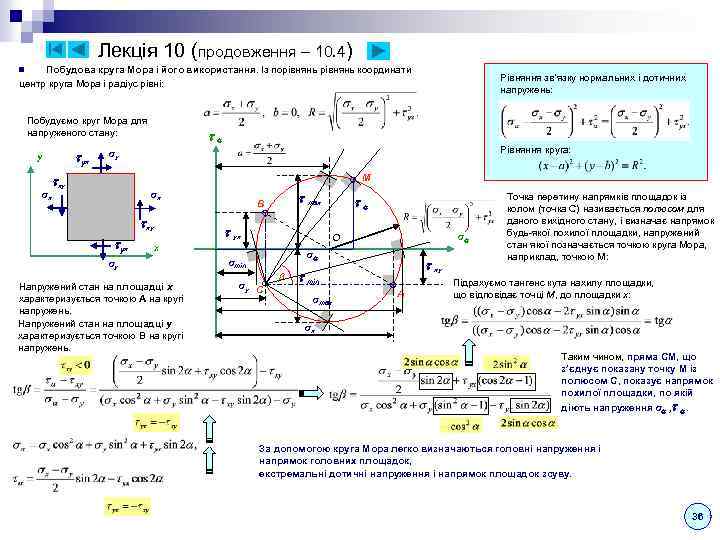Лекція 10 (продовження – 10. 4) Побудова круга Мора і його використання. Із порівнянь координати центр круга Мора і радіус рівні: n Побудуємо круг Мора для напруженого стану: yx у σx Рівняння зв’язку нормальних і дотичних напружень: Рівняння круга: σy M xy σx xy yx max B yx Напружений стан на площадці х характеризується точкою А на кругі напружень. Напружений стан на площадці у характеризується точкою В на кругі напружень. σ O x σy σ σmin σy С xy min σmax A Точка перетину напрямків площадок із колом (точка С) називається полюсом для даного вихідного стану, і визначає напрямок будь-якої похилої площадки, напружений стан якої позначається точкою круга Мора, наприклад, точкою М: Підрахуємо тангенс кута нахилу площадки, що відповідає точці М, до площадки х: σx Таким чином, пряма СМ, що з’єднує показану точку М із полюсом С, показує напрямок похилої площадки, по якій діють напруження σ , . За допомогою круга Мора легко визначаються головні напруження і напрямок головних площадок, екстремальні дотичні напруження і напрямок площадок зсуву. 36

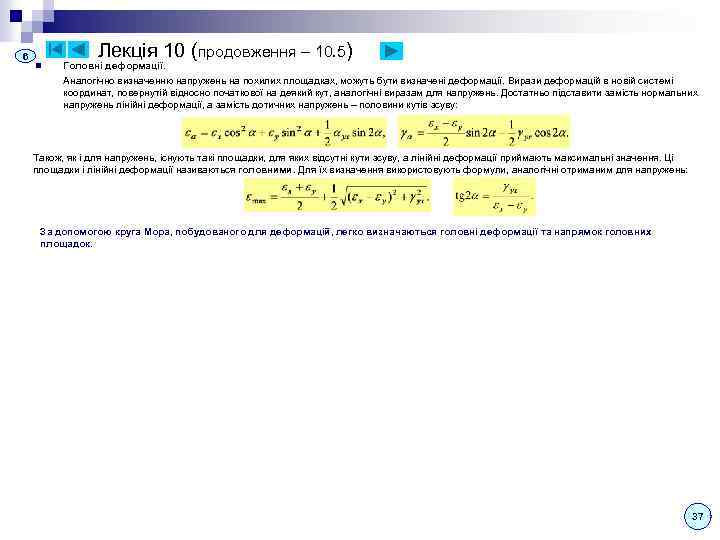Лекція 10 (продовження – 10. 5) 6 n Головні деформації. Аналогічно визначенню напружень на похилих площадках, можуть бути визначені деформації. Вирази деформацій в новій системі координат, повернутій відносно початкової на деякий кут, аналогічні виразам для напружень. Достатньо підставити замість нормальних напружень лінійні деформації, а замість дотичних напружень – половини кутів зсуву: Також, як і для напружень, існують такі площадки, для яких відсутні кути зсуву, а лінійні деформації приймають максимальні значення. Ці площадки і лінійні деформації називаються головними. Для їх визначення використовують формули, аналогічні отриманим для напружень: За допомогою круга Мора, побудованого для деформацій, легко визначаються головні деформації та напрямок головних площадок. 37

Лекція 11 n Деформації при об’ємному напруженому стані. Узагальнений закон Гука. При лінійному напруженому стані: – відносна поздовжня деформація; або – відносна поперечна деформація. Закон Гука в загальному вигляді Коефіцієнт Пуассона При об’ємному напруженому стані: Згідно з принципом незалежності дії сил, запишемо повні деформації у напрямку дії напруження σ1: a відповідно повна деформація тіла буде виглядати так: Це і є узагальнений закон Гука, в напруженнях, який дозволяє встановити взаємозв'язок між лінійними деформаціями і головними нормальними напруженнями. Цей закон Гука справедливий не тільки для головних площадок, але і для відносних деформацій по будьякому із трьох взаємно перпендикулярних напрямків. 38

Лекція 11 (продовження – 11. 2) n Об’ємна деформація. Об’ємний закон Гука. Узагальнений закон Гука дає можливість оцінити відносну зміну об'єму. Так, до деформування елемент займав об'єм У деформованому стані: Перемножимо дужки, нехтуючи величинами другого та третього порядку малості: Тоді Таким чином - відносна зміна об’єму Підставляємо деформації із узагальненого закону Гука в відносну зміну об’єму: - об’ємний закон Гука. Із цього співвідношення видно, що відносна зміна об'єму дорівнює нулю в двох випадках: 1) коли коефіцієнт Пуассона ν=0, 5 (гума); 2) при чистому зсуві, для якого , а При рівномірному всебічному стиску, коли: де називається модулем об'ємної деформації матеріалу. 39

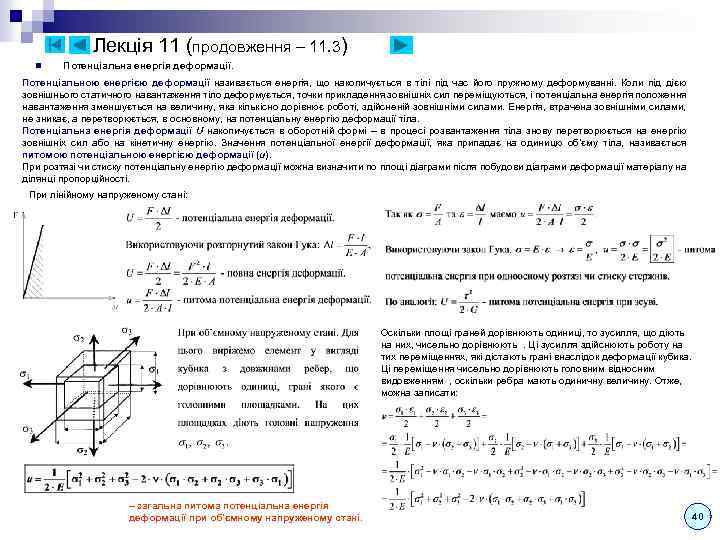Лекція 11 (продовження – 11. 3) n Потенціальна енергія деформації. Потенціальною енергією деформації називається енергія, що накопичується в тілі під час його пружному деформуванні. Коли під дією зовнішнього статичного навантаження тіло деформується, точки прикладення зовнішніх сил переміщуються, і потенціальна енергія положення навантаження зменшується на величину, яка кількісно дорівнює роботі, здійсненій зовнішніми силами. Енергія, втрачена зовнішніми силами, не зникає, а перетворюється, в основному, на потенціальну енергію деформації тіла. Потенціальна енергія деформації U накопичується в оборотній формі – в процесі розвантаження тіла знову перетворюється на енергію зовнішніх сил або на кінетичну енергію. Значення потенціальної енергії деформації, яка припадає на одиницю об’єму тіла, називається питомою потенціальною енергією деформації (и). При розтязі чи стиску потенціальну енергію деформації можна визначити по площі діаграми після побудови діаграми деформації матеріалу на ділянці пропорційності. При лінійному напруженому стані: Оскільки площі граней дорівнюють одиниці, то зусилля, що діють на них, чисельно дорівнюють. Ці зусилля здійснюють роботу на тих переміщеннях, які дістають грані внаслідок деформації кубика. Ці переміщення чисельно дорівнюють головним відносним видовженням , оскільки ребра мають одиничну величину. Отже, можна записати: – загальна питома потенціальна енергія деформації при об'ємному напруженому стані. 40

Лекція 11 (продовження – 11. 4) n Питома потенціальна енергія формозміни. При деформуванні елемента взагалі змінюється як його об’єм, так і форма: и = иv + иф. Безпосередньо визначити иф важко, тому знайдемо спочатку енергію зміни об’єму иv. Це можна зробити, виходячи з припущення про те, що в різних елементах при дії різних головних напружень значення иv буде однакове, якщо елементи будуть однаково змінювати об’єми εv. Крім розглядуваного елементу (назвемо його А) введемо ще допоміжний елемент А΄. Нехай А΄ – також одиничний кубик, але по його гранях діють однакові головні напруження. Тоді для цього елементу: - питома потенціальна енергія деформування, що йде на зміну об’єму. – питома потенціальна енергія, що витрачається на зміну форми елемента, що деформується. 41

Лекція 11 (продовження – 11. 5) 42

Лекція 11 (продовження – 11. 6) 43

Лекція 12 ■ Загальні поняття про теорії міцності - При випробуваннях матеріалів статичним навантаженням на центральне розтягування (стиснення) досягається граничний стан, що характеризується настанням текучості, появою значних залишкових деформацій і / або тріщин. Для пластичних матеріалів за граничну або небезпечну величину напружень приймається межа текучості Т, для крихких - межа міцності В. При експлуатації конструкцій в загальному випадку по площадках елементарного об’єму виникають нормальні і дотичні напруження, . пропорційні збільшенню навантаження. Значення кожного з напружень залежать від орієнтації розглянутих площадок. yz y σz σy yx xy zy zx z xz σx x σ2 σ3 σ2 σ1 σ3 σz Варіацією кутів повороту площадок можна визначити площадки, вільні від дотичних напружень, на яких виникають максимальні нормальні напруження. Такі площадки і напруження називаються головними (способи їх визначення для плоского напруженого стану були розглянуті на лекції 9 даного курсу). Саме головні напруження і можуть служити об'єктивною характеристикою напруженого стану в точці, оскільки вони є інваріантами - величинами, незалежними від орієнтації майданчиків. У результаті при оцінці міцності матеріалу замість розгляду 9 компонентів напруженого стану, що залежать від орієнтації елементарних площадок, можна розглядати всього 3 ( 1> 2> 3). При роботі конструкції під навантаженням деякі точки знаходяться в умовах плоского або просторового напруженого стану, для яких можливі самі різні співвідношення між головними напруженнями. Для визначення граничного (небезпечного) стану в точці (і тим самим всієї конструкції), слід було б порівняти ці σ1 напруження з граничними. Однак, практично це зробити неможливо, оскільки провести експерименти, подібні випробувань на центральний розтяг-стиск до руйнування, довелося б зробити для кожного з можливих співвідношень між головними напруженнями, не кажучи вже про те, що реалізувати ці співвідношення при випробуваннях технічно важко. Таким чином, необхідно мати можливість зіставити міцність матеріалу при плоскому та просторовому напруженому стані з результатами випробувань при одноосьовому розтяганні-стисканні. Це завдання вирішується за допомогою висування гіпотези по якомусь одному критерії, що визначає умову переходу матеріалу в небезпечний стан, що становить основу відповідної теорії міцності. σz З використанням того чи іншого критерію головні напруження, що виникають в конструкції, вдається пов'язати з граничними механічними характеристиками, одержуваними при одноосьовому випробуванні. В результаті визначається деяке еквівалентне напруження, що характеризує аналізований напружений стан, який можна порівнювати з граничним або допустимими напруженнями при одноосьовому розтяганні-стисканні. ■ Критерій руйнування шляхом відриву (крихке руйнування) - Можливе часткове або повне руйнування тіла. Розрізняють руйнування в'язке і крихке, які можуть проявлятися як одночасно, так і послідовно. Крихке руйнування відбувається в результаті швидкого розповсюдження тріщини після незначної пластичної деформації або без неї. В останньому випадку руйнування називається ідеально крихким. При крихкому руйнуванні швидкість поширення тріщини велика (0, 2 -0, 5 швидкості звуку), а злам має кристалічний вигляд. При квазіхрупкому руйнуванні спостерігається деяка пластична зона перед краєм тріщини. Крихкі тріщини можуть виникати при середніх напруженнях, що не перевищують межу текучості. Часто тріщини повільно ростуть і процес їх росту може становити до 90% часу "Життя" деталі. Тому має значення не стільки факт виникнення тріщини, скільки темп її зростання. 44

Лекція 12 (продовження – 12. 2) Поля нормальних і дотичних напружень у вершині тріщини описуються деякими функціями, отримані методами теорії пружності, в які входить коефіцієнт інтенсивності напружень, мають різні значення в залежності від типу деформації тріщин: I - тріщина нормального відриву; II - тріщина плоского зсуву; III - тріщина антиплоского зсуву. Нижче розглядаються три теорії міцності, що ґрунтуються на критерії руйнування шляхом відриву. I теорія міцності - Теорія найбільших нормальних напружень: гіпотеза переходу матеріалу в небезпечний стан досягнення одного з головних напружень граничного (небезпечного) значення. З використанням цього критерію - при умова міцності має вигляд: Перша умова використовується при 1> 2> 3 > 0, друга – при 3 < 0, якщо | 3| > | 1| - при Теорія враховує лише одне з головних напружень, експериментально підтверджується лише для крихких матеріалів за умови, що одне з головних напружень значно більше за інших. II теорія міцності - Теорія найбільших деформацій: гіпотеза переходу матеріалу в небезпечний стан - досягнення деформаціями граничного (небезпечного) значення. Тут при обчисленні максимальної деформації беруть участь всі три головні З використанням цього критерію напруження: умова міцності має вигляд: Отже, умова міцності, виражена через головні напруження набуває вигляду: Теорія враховує всі три головні напруження, але експериментально підтверджується лише для крихких матеріалів за умови, що всі головні напруження негативні. Таким чином, I і II теорії міцності можуть застосовуватися лише для крихких матеріалів. Зауважимо, що крихкі матеріали часто мають різні механічні характеристиками при розтягуванні і стисненні. Тому в цих випадках необхідно використовувати відповідні розрахункові (допустимі) напруження. Теорія міцності Мора - використовує припущення, що напруження 2 мало впливає на міцність матеріалу (в межах 15%). Таким чином розрахунок міцності в загальному випадку тривісного напруженого стану зводиться до розрахунку міцності при двохосьовому напруженому стані. Це не означає, що в умові для II теорії просто слід прирівняти 2 нулю. Тут розрахункове напруження визначається з урахуванням двох випробувань: на розтяг - р і на стиск - с. 45

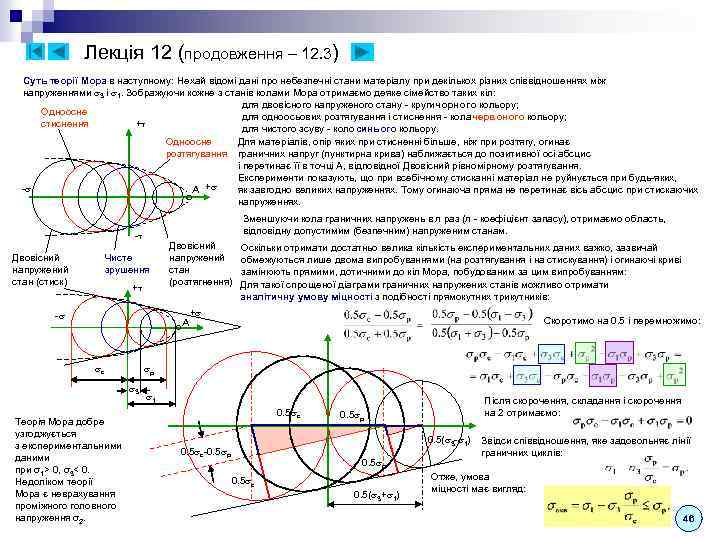Лекція 12 (продовження – 12. 3) Суть теорії Мора в наступному: Нехай відомі дані про небезпечні стани матеріалу при декількох різних співвідношеннях між напруженнями 3 і 1. Зображуючи кожне з станів колами Мора отримаємо деяке сімейство таких кіл: для двовісного напруженого стану - круги чорного кольору; Одноосне для одноосьових розтягування і стиснення - кола червоного кольору; стиснення + для чистого зсуву - коло синього кольору. Для матеріалів, опір яких при стисненні більше, ніж при розтягу, огинає Одноосне розтягування граничних напруг (пунктирна крива) наближається до позитивної осі абсцис і перетинає її в точці A, відповідної Двовісний рівномірному розтягування. Експерименти показують, що при всебічному стисканні матеріал не руйнується при будь-яких, - A + як завгодно великих напруженнях. Тому огинаюча пряма не перетинає вісь абсцис при стискаючих напруженнях. Зменшуючи кола граничних напружень в n раз (n - коефіцієнт запасу), отримаємо область, відповідну допустимим (безпечним) напруженим станам. - Двовісний напружений стан (стиск) Чисте зрушення + - Двовісний напружений стан (розтягнення) A с + Скоротимо на 0. 5 і перемножимо: р 3 Теорія Мора добре узгоджується з експериментальними даними при σ1> 0, σ3< 0. Недоліком теорії Мора є неврахування проміжного головного напруження σ2. Оскільки отримати достатньо велика кількість експериментальних даних важко, зазвичай обмежуються лише двома випробуваннями (на розтягування і на стискування) і огинаючі криві замінюють прямими, дотичними до кіл Мора, побудованим за цим випробуванням: Для такої спрощеної діаграми граничних напружених станів можливо отримати аналітичну умову міцності з подібності прямокутних трикутників: 1 0. 5 с Після скорочення, складання і скорочення на 2 отримаємо: 0. 5 р 0. 5( 3 - 1) 0. 5 с-0. 5 р 0. 5 с 0. 5( 3+ 1) Звідси співвідношення, яке задовольняє лінії граничних циклів: Отже, умова міцності має вигляд: 46

Лекція 12 (продовження – 12. 4) ■ Критерій пластичного стану - При випробуваннях матеріалів було виявлено, що в пластичному стані максимальне дотичне напруження має одне і те ж значення для даного матеріалу. У результаті, в якості наступної гіпотези переходу матеріалу в граничний стан можна вибрати досягнення найбільших дотичних напружень граничного (небезпечного) значення (критерій пластичності). Ця гіпотеза лягла в основу III теорії міцності. З використанням цього критерію умова міцності має вигляд: У разі плоского напруженого стану: При згині з крученням: Експериментальні дані показують хороший збіг результатів для пластичних матеріалів. Недоліком III теорії, як і вище вказаних теорій, є неврахування середнього головного напруження 2. ■ IV теорія міцності (енергетична) - Першою спробою зв'язати всі три головні напруження було висунення гіпотези переходу в граничний стан питомої потенційної енергії деформації деякого граничного значення. Експерименти показали, що при всебічному стисканні, пластичні деформації не виникають, хоча при цьому накопичується велика питома потенційна енергія. У зв'язку з цим була висунута гіпотеза про те, що граничний стан обумовлюється досягненням граничного значення лише тієї частини питомої потенційної енергії деформації, яка пов'язана зі зміною форми: де - повна питома потенційна енергія. Підстановка узагальненого закону Гука дає такий вираз для повної питомої потенційної енергії: Питому потенційну енергію, витрачену на зміну об'єму, можна отримати з цього виразу, приймаючи 1 = 2 = 3= о: Приймемо: Питома потенційна енергія, що витрачається на зміну форми: 47

Лекція 12 (продовження – 12. 5) Отриманий вираз після приведення до спільного знаменника, розкриття квадрата суми, множення і віднімання дає: або Зауваження: Ці ж співвідношення можна отримати безпосередньо з виразу для повної питомої енергії деформації задаючи по головних площадках напруження, рівні різниці діючих головних напружень і середнього напруження: 1’ = 1 - о, 2’ = 2 - о, 3’ = 3 - о: і підставляючи значення середнього напруження: Для одноосного розтягування при настанні текучості 1 = Т , 2 = 3 = 0 питома потенційна енергія складає величину: Прирівнюючи вирази питомої потенційної енергії зміни форми для тривісного напруженого стану і для одноосного, отримуємо еквівалентне напруження: або При згині з крученням: Як і теорія III, енергетична теорія дає хороший збіг результатів з експериментальними даними для пластичних матеріалів. ■ Поняття про нові теорії міцності та механіки руйнування - Гранична поверхня, відповідна умові появи масових пластичних деформацій і по IV теорії, визначається рівнянням: Рівняння відповідає поверхні кругового циліндра радіуса , вісь якого рівно нахилена до координатних осей 1, 2 і 3. Критерій, використаний в ІІІ теорії, дає поверхню правильної шестигранної призми, вписаної в циліндр, тобто гранична область майже співпадає з областю по IV теорії. Критерій найбільших нормальних напружень (І теорія міцності дає куб із ребром рівним о. Новітні теорії міцності ґрунтуються на на виборі різних варіантів граничної поверхні f( 1, 2, 3) = 0, при якій найбільш повно можливо врахувати особливості опору даного класу матеріалів в умовах складного напруженого стану. Наприклад, у композитних (армованих) матеріалах, руйнування може частково проходити за рахунок розриву волокон, а також частково за рахунок сколювання матриці. У випадку ортотропних матеріалів, що мають різні границі міцності при стиску і розтязі, умова міцності містить константи із відповідних дослідів, тобто використовується не один розрахунковий опір, а два і більше. 48

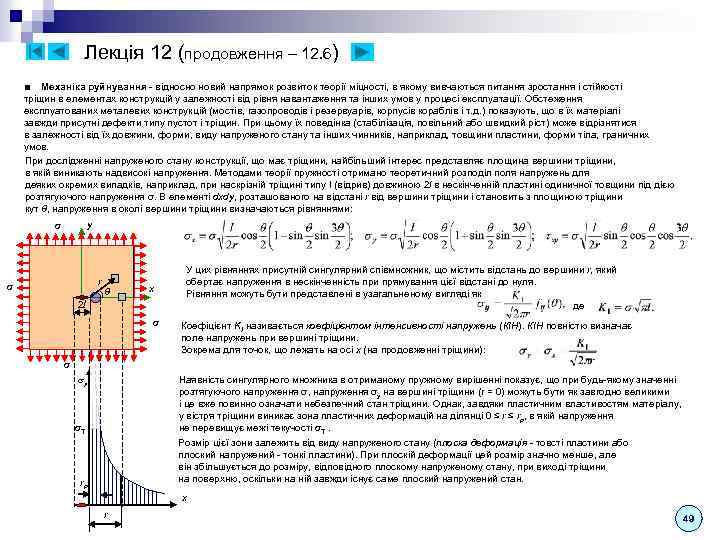Лекція 12 (продовження – 12. 6) ■ Механіка руйнування - відносно новий напрямок розвиток теорії міцності, в якому вивчаються питання зростання і стійкості тріщин в елементах конструкцій у залежності від рівня навантаження та інших умов у процесі експлуатації. Обстеження експлуатованих металевих конструкцій (мостів, газопроводів і резервуарів, корпусів кораблів і т. д. ) показують, що в їх матеріалі завжди присутні дефекти типу пустот і тріщин. При цьому їх поведінка (стабілізація, повільний або швидкий ріст) може відрізнятися в залежності від їх довжини, форми, виду напруженого стану та інших чинників, наприклад, товщини пластини, форми тіла, граничних умов. При дослідженні напруженого стану конструкції, що має тріщини, найбільший інтерес представляє площина вершини тріщини, в якій виникають надвисокі напруження. Методами теорії пружності отримано теоретичний розподіл поля напружень для деяких окремих випадків, наприклад, при наскрізній тріщині типу I (відрив) довжиною 2 l в нескінченній пластині одиничної товщини під дією розтягуючого напруження σ. В елементі dxdy, розташованого на відстані r від вершини тріщини і становить з площиною тріщини кут θ, напруження в околі вершини тріщини визначаються рівняннями: y σ r σ θ x 2 l σ У цих рівняннях присутній сингулярний співмножник, що містить відстань до вершини r, який обертає напруження в нескінченність при прямування цієї відстані до нуля. Рівняння можуть бути представлені в узагальненому вигляді як де Коефіцієнт KI називається коефіцієнтом інтенсивності напружень (КІН). КІН повністю визначає поле напружень при вершині тріщини. Зокрема для точок, що лежать на осі x (на продовженні тріщини): σ y Наявність сингулярного множника в отриманому пружному вирішенні показує, що при будь-якому значенні розтягуючого напруження σ, напруження σy на вершині тріщини (r = 0) можуть бути як завгодно великими і це вже повинно означати небезпечний стан тріщини. Однак, завдяки пластичним властивостям матеріалу, у вістря тріщини виникає зона пластичних деформацій на ділянці 0 ≤ rp, в якій напруження не перевищує межі текучості σТ. Розмір цієї зони залежить від виду напруженого стану (плоска деформація - товсті пластини або плоский напружений - тонкі пластини). При плоскій деформації цей розмір значно менше, але він збільшується до розміру, відповідного плоскому напруженому стану, при виході тріщини на поверхню, оскільки на ній завжди існує саме плоский напружений стан. σТ rp x r 49

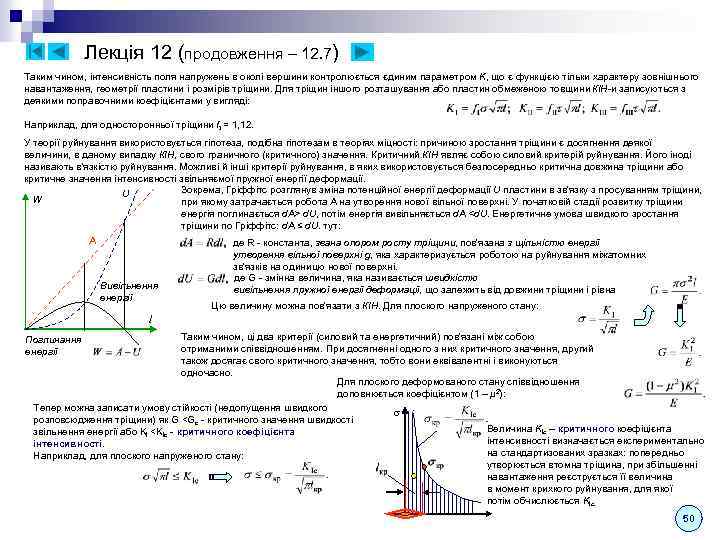Лекція 12 (продовження – 12. 7) Таким чином, інтенсивність поля напружень в околі вершини контролюється єдиним параметром K, що є функцією тільки характеру зовнішнього навантаження, геометрії пластини і розмірів тріщини. Для тріщин іншого розташування або пластин обмеженою товщини КІН-и записуються з деякими поправочними коефіцієнтами у вигляді: Наприклад, для односторонньої тріщини f. I = 1, 12. У теорії руйнування використовується гіпотеза, подібна гіпотезам в теоріях міцності: причиною зростання тріщини є досягнення деякої величини, в даному випадку КІН, свого граничного (критичного) значення. Критичний КІН являє собою силовий критерій руйнування. Його іноді називають в'язкістю руйнування. Можливі й інші критерії руйнування, в яких використовується безпосередньо критична довжина тріщини або критичне значення інтенсивності звільняємої пружної енергії деформації. Зокрема, Гріффітс розглянув зміна потенційної енергії деформації U пластини в зв'язку з просуванням тріщини, U W при якому затрачається робота A на утворення нової вільної поверхні. У початковій стадії розвитку тріщини енергія поглинається d. A> d. U, потім енергія вивільняється d. A

Лекція 13 Поняття про чистий зсув - Крім деформацій розтягування або стиснення матеріал завантаженого елемента конструкції може спиймати деформацію зсуву. Прикладом цьому може служити напружено-деформований стан елемента стінки балки в довільному перерізі, розглянутий на лекції по темі “Згин”. Там же було показано, що в опорних перерізах на нейтральній осі на гранях елемента відсутні нормальні напруження, а дотичні напруження максимальні. Іншим прикладом, можна сказати класичним, є кручення тонкостінної труби, z zy z y при якому будь-який елемент знаходиться тільки під дією дотичних напружень. Напружено-деформований стан, що характеризується тим, що на гранях yz елемента виникають тільки дотичні напруження, називають чистим зсувом. dz n Закон Гука при зсуві - Деформації чистого зсуву експериментально вивчаються шляхом кручення трубчастих зразків. Експериментальна діаграма зсуву, y пов'язує напруження і кут зсуву, та для пластичної сталі має такий же характер dy зміни, як і діаграма розтягування: A zy до напруження пц , названого межею пропорційності x при зсуві справедлива лінійна залежність (закон Гука при зсуві) : Тут - відносний кут зсуву: G – модуль зсуву. Т пц yz y Дотичне напруження, при якому кут зсуву зростає при постійному напруженні називається межею текучості при зсуві. ■ Зв'язок між модулем зсуву і модулем пружності при розтягуванні - Модуль зсуву і модуль пружності при розтягуванні є фізичними постійними матеріалу, що характеризують жорсткість у кожному з цих двох видів деформації. Оскільки подовження діагоналі елемента, викликане зсувом, може бути отримано також розтягуванням цього волокна під дією нормальних напружень, ці константи повинні бути пов'язані між собою деяким співвідношенням: Подовження діагоналі елемента внаслідок деформації зсуву (dy = dz): tg = G ds y ds dz A Подовження діагоналі елемента внаслідок деформації розтягування (σ1 = , σ2 = - ): dy або Таким чином існує співвідношення між модулем зсуву і модулем пружності при розтягуванні, використовуючи коефіцієнт Пуассона. Будь-яку з цих величин можна визначити, якщо відомі дві інші. 51

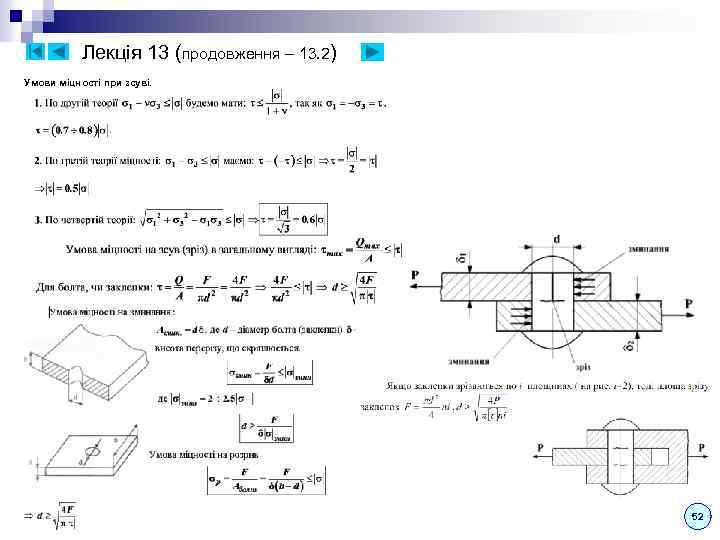Лекція 13 (продовження – 13. 2) Умови міцності при зсуві. 52

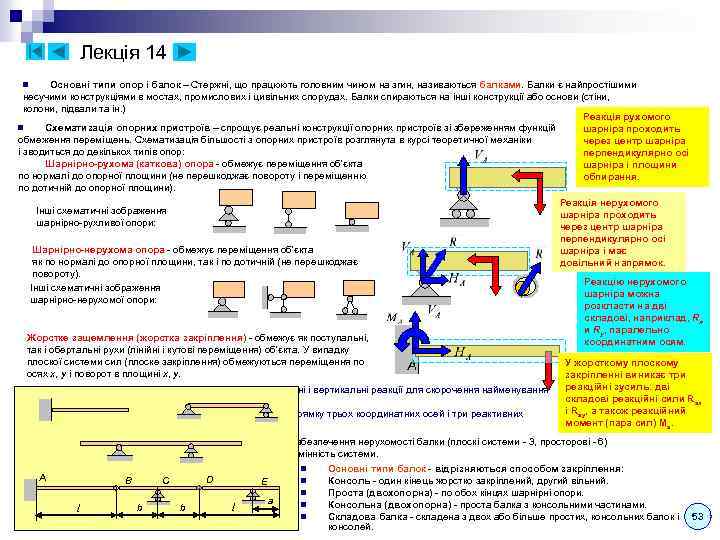Лекція 14 Основні типи опор і балок – Стержні, що працюють головним чином на згин, називаються балками. Балки є найпростішими несучими конструкціями в мостах, промислових і цивільних спорудах. Балки спираються на інші конструкції або основи (стіни, колони, підвали та ін. ) Реакція рухомого n Схематизація опорних пристроїв – спрощує реальні конструкції опорних пристроїв зі збереженням функцій шарніра проходить обмеження переміщень. Схематизація більшості з опорних пристроїв розглянута в курсі теоретичної механіки через центр шарніра і зводиться до декількох типів опор: перпендикулярно осі Шарнірно-рухома (каткова) опора - обмежує переміщення об'єкта шарніра і площини по нормалі до опорної площини (не перешкоджає повороту і переміщенню обпирання. по дотичній до опорної площини). Реакція нерухомого Інші схематичні зображення шарніра проходить шарнірно-рухливої опори: через центр шарніра перпендикулярно осі Шарнірно-нерухома опора - обмежує переміщення об'єкта шарніра і має як по нормалі до опорної площини, так і по дотичній (не перешкоджає довільний напрямок. повороту). Реакцію нерухомого Інші схематичні зображення шарніра можна шарнірно-нерухомої опори: розкласти на дві складові, наприклад, Rx и Ry, паралельно Жорстке защемлення (жорстка закріплення) - обмежує як поступальні, координатним осям. так і обертальні рухи (лінійні і кутові переміщення) об'єкта. У випадку плоскої системи сил (плоске закріплення) обмежуються переміщення по У жорсткому плоскому A осях x, у і поворот в площині x, у. закріпленні виникає три реакційні зусиль: дві В опорі матеріалів і далі в будівельній механіці горизонтальні і вертикальні реакції для скорочення найменування складові реакційні сили Rаx часто позначають як HA (horizontal) та VA (vertical). і Rаy, а також реакційний У разі просторової системи сил виникають три реакції у напрямку трьох координатних осей і три реактивних момент (пара сил) Mа. моменту (пар сил) щодо цих осей. n У всіх випадках число зв'язків повинно бути достатнім для забезпечення нерухомості балки (плоскі системи - 3, просторові - 6) і способи влаштування зв'язків повинні виключати миттєву змінність системи. Приклади миттєво-змінюваних систем: n Основні типи балок - відрізняються способом закріплення: A D C B n Консоль - один кінець жорстко закріплений, другий вільний. E n Проста (двохопорна) - по обох кінцях шарнірні опори. a n Консольна (двохопорна) - проста балка з консольними частинами. l b b l n Складова балка - складена з двох або більше простих, консольних балок і консолей. 53

Лекція 14 (продовження – 14. 2) n n Визначення опорних реакцій в балках - виконується методами теоретичної механіки. . Рівняння рівноваги можуть бути складені у вигляді однієї з трьох форм : Оскільки знайдені опорні реакції будуть використовуватися у подальших розрахунках (побудова епюр внутрішніх зусиль, визначення напружень і переміщень) слід активно користуватися цими формами рівнянь так, щоб в кожне з рівнянь входила лише одна визначуванареакція, щоб виключити підстановку раніше знайдених і неперевірених реакцій. Після незалежного обчислення всіх реакцій обов'язково повинна бути виконана перевірка складанням такого рівняння рівноваги, в якому б були присутні всі або більшість із знайдених реакцій. Оскільки балки несуть переважно вертикальне навантаження, то в загальному випадку рекомендується скористатись формою II і перевірити вертикальні реакції складанням рівняння у проекціях на вертикальну вісь. Пам'ятайте, що невірно знайдені реакції у будь-якому випадку приведуть до невірних результатів при побудові епюр, визначенні напружень і переміщень! n Внутрішні зусилля при згині - При згині виникають у загальному випадку згинальні моменти Mx, My і поперечні сили Qx, Qy. Якщо в поперечному перерізі виникає тільки один згинаючий момент Mx, то такий згин називається чистим. Mx Mx + У більшості випадків додатково до згинаючого моменту виникає поперечна сила Qy, і такий згин називається поперечним. n Якщо зовнішнє навантаження і реакційні зусилля лежать в одній площині, то такий згин називається плоским. n Правила знаків для згинального моменту - Згинальний момент приймається позитивним, Mx Mx З використанням цих основних залежностей балки викривляється якщо він згинає елемент балки так, що нижні волокна виявляються розтягнутими, тобто вісь отримуємо: + Qy опуклістю вниз. n Правила знаків для поперечної сили - Поперечна сила вважається позитивною, якщо вона Qy прагне повернути елемент балки по ходу годинникової стрілки. Qy ■ Диференціальні залежності при згині - пов'язують внутрішні зусилля між собою в перерізі і Друга похідна від згинального моменту навантаженням. Виділимо з балки елемент довжиною dz, що знаходиться під дією зовнішнього вертикального Qy y по поздовжній координаті дорівнює рівномірно розподіленого навантаженням q, і замінимо дію відкинутих частин внутрішніми зусиллями: qy інтенсивності розподіленого навантаження. Виділений елемент знаходиться в рівновазі Mx Qy Mx+d. Mx і задовольняє рівняння рівноваги: O z З першого рівняння отримуємо: Qy+d. Qy З другого рівняння, нехтуючи значеннями dz другого порядку малості отримуємо: Похідна від поперечної сили Похідна від згинального моменту по поздовжній координаті дорівнює 54 інтенсивності розподіленого навантаження. по поздовжній координаті дорівнює поперечної силі. n

Лекція 14 (продовження – 14. 3) Побудова епюр згинаючих моментів і поперечних сил - принципово нічим не відрізняється від побудови епюри поздовжніх сил і крутних моментів. Позитивні значення поперечної сили Qy відкладаються нагору від горизонтальної базової лінії, а негативні - вниз. Позитивні значення згинальних моментів Mx відкладаються вгору - з боку стиснутого волокна. Таким чином розташування ординат епюри Mx вказують, які волокна стиснуті. Примітка: Це правило прийнято в машинобудівних та авіаційних вузах, у той час, як в будівельних і транспортних вузах використовується Використовуючи отримані вирази для поперечної сили і згинального моменту побудуємо епюру зворотне правило (позитивний момент відкладається з боку розтягнутого волокна). поперечних сил і згинальних моментів, підставляючи значення реакцій і координати 2: Нехай балка навантажена рівномірно розподіленим навантаженням q, зосередженої силою F = qa і обертовим моментом M=qaпочатку і кінця ділянок. У разі квадратичної зміни величини (згинальний момент на першій ділянці) додатково y х1 I х2 II х3 III F 1. визначаємо q підставляється: координата точки всередині інтервалу, наприклад, посередині. M опорні реакції HA A VB B Відкладаючи на кожній з ділянці значення поперечних сил і згинального моменту = 1, 75 qa z в деякому вибраному масштабі отримуємо епюри Qy і Mx: VA I II III VA = 1, 25 qa VB 2 кількість ділянок– 3. 2 a 2 a 2 a Із другого та третього 3. Проведемо отримуємо: першій ділянці та визначимо поточну координату перерізу та межі її зміни: y рівняння переріз І-І на 0 х1 2 a. Mx. I-I q A 4. Відкинемо праву частину, замінивши її дію поперечною силою Qy. I-I та згинаючим моментом Mx. I-I та C складемо рівняння рівноваги в проекціях і в моментах відносно вісі х, що проходить через центр Виконуємо контроль: VA поточного перерізу (тобто відносно точки С): Qy. I-I Отримані вирази показують, що: q поперечна сила в перерізі дорівнює Mx. II-II A алгебраїчній сумі проекцій Звідси отримуємо : D Q III-III F на вертикальну вісь зовнішніх сил, y VA Qy. II-II взятих по одну сторону від перерізу, Властивості ділянок Повторюємо кроки 3 та 4 для наступних епюр: : згинальний момент - алгебраїчній. E сумі III-III 3. Проведемо переріз II-II на 1. Рівномірно розподілене навантаження на ділянці другій ділянці і визначимо поточну координату перерізу і межі її Mx моментів відносно горизонтальної осі, що своєї дії викликає на епюрі Q похилу зміни : 0 х2 2 a. проходить через центр ваги перерізу, пряму лінію, спадаючу в сторону дії навантаження, 4. Відкинемо праву частину, замінимо її дію поперечної силою Qy. II-II і згинаючим моментом Mx. II-II зовнішніх сил взятих по одну сторону від а в епюрі M в моментах щодо осі проти дії навантаження. і складемо рівняння рівноваги напроекціях-і параболу з опуклістю x, що проходить через перерізу! 2. Зосереджена сила викликає на епюрі Q центр поточного перерізу (тобто відносно точки D): стрибок в точці прикладання сили в бік дії сили, а на епюрі М - перелом проти дії навантаження. Звідси отримуємо: 3. Зосереджений момент не викликає на епюрі Q в точці його програми ніяких особливостей, Знак доданків позитивний, якщо а на епюрі M х 2 a): розглянутий фактор, будучи Аналогічно отримуємо для ділянки 3 (0 викликає стрибок. 3 прикладений до поперечного перерізу Дивіться і дивуйтеся! іншої частини, відповідаючи позитивному напрямку визначаємого внутрішнього зусилля. 55 n

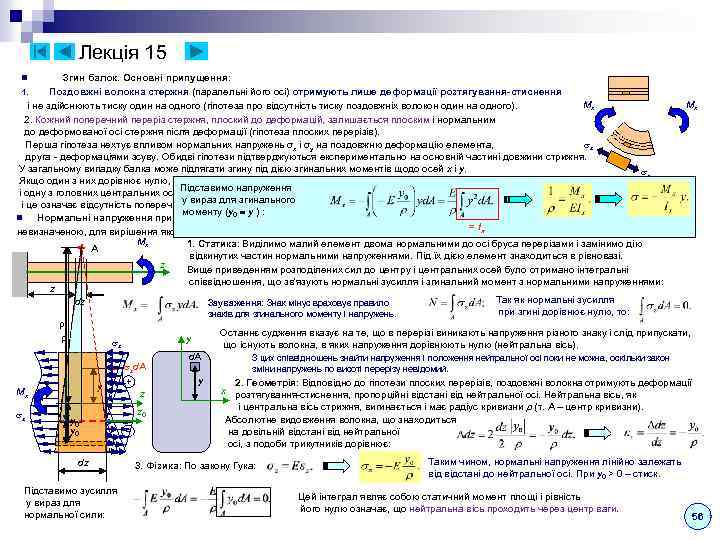Лекція 15 Згин балок. Основні припущення: Поздовжні волокна стержня (паралельні його осі) отримують лише деформації розтягування-стиснення Mx Mx і не здійснюють тиску один на одного (гіпотеза про відсутність тиску поздовжніх волокон один на одного). 2. Кожний поперечний переріз стержня, плоский до деформацій, залишається плоским і нормальним до деформованої осі стержня після деформації (гіпотеза плоских перерізів). z Перша гіпотеза нехтує впливом нормальних напружень σx і σy на поздовжню деформацію елемента, друга - деформаціями зсуву. Обидві гіпотези підтверджуються експериментально на основній частині довжини стрижня. У загальному випадку балка може підлягати згину під дією згинальних моментів щодо осей x і y. z Якщо один з них дорівнює нулю, а інший лежить у головній площині перерізу (площині, що проходить через вісь стержня Підставимо напруження і одну з головних центральних осей інерції), то такий згин називається плоским згином. Якщо при цьому згинальний момент постійний, у вираз для згинального і це означає відсутність поперечної сили, то такий вигин називається чистим згином. моменту (y 0 y ) : n Нормальні напруження при чистому згині - Як вказувалося раніше, задача визначення напружень є статично = Ix невизначеною, для вирішення якої необхідно послідовно розглянути три сторони задачі: Mx 1. Статика: Виділимо малий елемент двома нормальними до осі бруса перерізами і замінимо дію A відкинутих частин нормальними напруженнями. Під їх дією елемент знаходиться в рівновазі. z Вище приведенням розподілених сил до центру і центральних осей було отримано інтегральні співвідношення, що зв'язують нормальні зусилля і згинальний момент з нормальними напруженнями: z Так як нормальні зусилля dz Зауваження: Знак мінус враховує правило при згині дорівнює нулю, то: знаків для згинального моменту і напружень. Останнє судження вказує на те, що в перерізі виникають напруження різного знаку і слід припускати, y z що існують волокна, в яких напруження дорівнюють нулю (нейтральна вісь). d. A З цих співвідношень знайти напруження і положення нейтральної осі поки не можна, оскільки закон zd. A зміни напружень по висоті перерізу невідомий. y + 2. Геометрія: Відповідно до гіпотези плоских перерізів, поздовжні волокна отримують деформації y x розтягування-стиснення, пропорційні відстані від нейтральної осі. Нейтральна вісь, як Mx z і центральна вісь стрижня, вигинається і має радіус кривизни (т. А – центр кривизни). z 0 z Абсолютне видовження волокна, що знаходиться y 0 – на довільній відстані від нейтральної осі, з подоби трикутників дорівнює: n 1. dz Підставимо зусилля у вираз для нормальної сили: 3. Фізика: По закону Гука: Таким чином, нормальні напруження лінійно залежать відстані до нейтральної осі. При y 0 > 0 – стиск. Цей інтеграл являє собою статичний момент площі і рівність його нулю означає, що нейтральна вісь проходить через центр ваги. 56

Лекція 15 (продовження – 15. 2) Момент опору при згині - З формули напружень при згині випливає, що найбільші (позитивні - розтягуючі) і найменші (негативні – стискаючі) напруження в поперечному перерізі виникають в точках, найбільш віддалених від нейтральної осі, розташованих по обидві сторони від неї: n При симетричному перерізі відносно нейтральної осі абсолютні величини найбільших розтягуючих і стискаючих напружень рівні і можуть бути визначені за формулою: В інших випадках необхідно спеціально шукати ymax , але формула залишається вірною. Величина, що залежить тільки від розмірів і форми поперечного перерізу, називається осьовим моментом опору: З використанням осьового моменту опору максимальні напруження обчислюються як: Моментом опору зручно користуватися при розрахунку на міцність (підборі перерізу) балки при згині. Звичайно, для цього моменти опору попередньо обчислюються для типових і прокатних перерізів за попередньою формулою. Момент опору типових і прокатних перерізів: 1. Прямокутний переріз: 2. Круглий переріз: n y y x h d R b n x 3. Для прокатних перерізів всі геометричні характеристики, в тому числі і моменти опору, вже обчислені та зібрані до спеціальних таблиць - сортаменту. У всіх випадках, крім круглого перерізу, потрібно використовувати моменти опору, відповідні орієнтації площини дії згинального моменту. Наприклад, при дії на балку прямокутного перерізу моменту My при обчисленні максимальних нормальних напружень необхідно використовувати Wy: Умова міцності по нормальним напруженням: Максимальні напруження не повинні перевищувати розрахункових або допустимих напружень. Звідси при підборі перерізу визначається необхідна величина моменту опору для прокатних перерізів або характерних розмірів для інших перерізів: У випадку, наприклад, прямокутного перерізу необхідно задати один з розмірів або співвідношення між ними. Нехай h / b = k. Тоді необхідна висота перерізу: 57

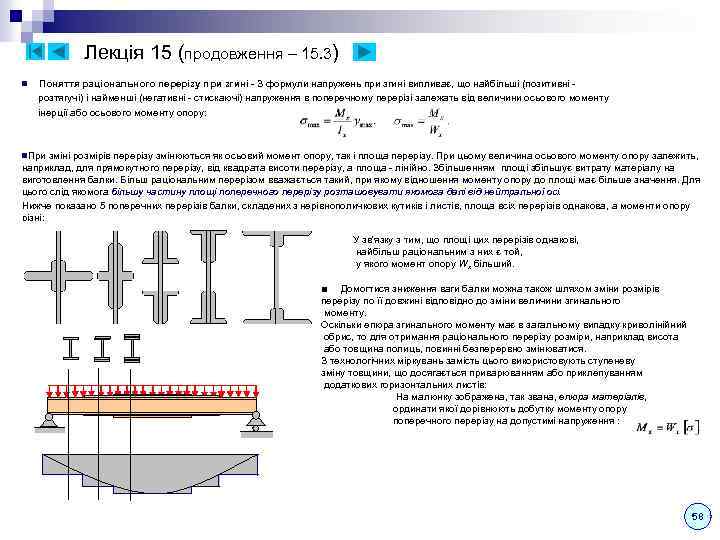Лекція 15 (продовження – 15. 3) n Поняття раціонального перерізу при згині - З формули напружень при згині випливає, що найбільші (позитивні розтягучі) і найменші (негативні - стискаючі) напруження в поперечному перерізі залежать від величини осьового моменту інерції або осьового моменту опору: n. При зміні розмірів перерізу змінюються як осьовий момент опору, так і площа перерізу. При цьому величина осьового моменту опору залежить, наприклад, для прямокутного перерізу, від квадрата висоти перерізу, а площа - лінійно. Збільшенням площі збільшує витрату матеріалу на виготовлення балки. Більш раціональним перерізом вважається такий, при якому відношення моменту опору до площі має більше значення. Для цього слід якомога більшу частину площі поперечного перерізу розташовувати якомога далі від нейтральної осі. Нижче показано 5 поперечних перерізів балки, складених з нерівнополичкових кутиків і листів, площа всіх перерізів однакова, а моменти опору різні: У зв'язку з тим, що площі цих перерізів однакові, найбільш раціональним з них є той, у якого момент опору Wx більший. ■ Домогтися зниження ваги балки можна також шляхом зміни розмірів перерізу по її довжині відповідно до зміни величини згинального моменту. Оскільки епюра згинального моменту має в загальному випадку криволінійний обрис, то для отримання раціонального перерізу розміри, наприклад висота або товщина полиць, повинні безперервно змінюватися. З технологічних міркувань замість цього використовують ступеневу зміну товщини, що досягається приварюванням або приклепуванням додаткових горизонтальних листів: На малюнку зображена, так звана, епюра матеріалів, ординати якої дорівнюють добутку моменту опору поперечного перерізу на допустимі напруження : 58

Лекція 15 (продовження – 15. 4) Прямий поперечний згин - в поперечному перерізі балки, крім згинального моменту, діє також поперечна сила. При прямому поперечному згині згинальний момент діє в площині, що збігається з однією з головних площин інерції поперечного перерізу балки. Поперечна сила при цьому зазвичай паралельна площині дії згинального моменту. n ■ Дотичні напруження при поперечному згині - У загальному випадку при поперечному згині балок довільного профілю можуть виникати дві компоненти повного дотичного напруження в перерізі. Компонента zx для такого перерізу не може бути знайдена методами опору матеріалів. Дотичні напруження zy, що виникають в поперечному перерізі, пов'язані з поперечною силою, що діє в цьому перерізі бруса, інтегральною залежністю: Оскільки закон зміни дотичних напружень по перерізу невідомий, F Mx то з цього рівняння знайти дотичні напруження для відомої поперечної сили не можна. Qy Mx+d. Mx z Виділимо малий елемент двома нормалями до осі бруса і замінимо дію відкинутих частин нормальними напруженнями та дотичними напруженнями. Під їх дією елемент знаходиться в рівновазі. Qy z dz zy z+d z zy yz dz A 1 Aвідс zx zy d. A y z b При дії поперечної сили згинальний момент у перерізі, віддаленому на відстані dz від іншого перерізу, має приріст d. Mx. y згідно залежності x нормальні напруження також отримують збільшення : Відсічемо від розглянутого елемента деяку її частину горизонтальною площиною і замінимо її дію дотичними напруженнями (нормальні напруження відповідно до гіпотезою про відсутність здавлювання поздовжніх волокон не розглядаються). Залишений елемент як і раніше знаходиться в рівновазі. Рівняння рівноваги в проекції на вісь z: или Тут Aвідс – площа відсіченої частини поперечного перерізу, A 1 – площа горизонтального перерізу елемента, що дорівнює bdz. Перенесемо перший інтеграл в праву частину і підставимо в нього вираз для нормальних напружень: Приріст згинального моменту і осьовий момент інерції перерізу не залежать від площі відсіченої частини і їх можна винести за знак інтеграла. Залишений підінтегральної вираз співпадає з виразом для статичного моменту площі відсіченої частини поперечного перерізу: Вважаючи дотичні напруження постійними за площею A 1, що відповідає припущенням сталості деформацій зсуву по ширині поперечного перерізу, враховуючи закон парності дотичних переміщень і диференціальну залежність або поперечної сили, отримуємо: - формула Журавського 59

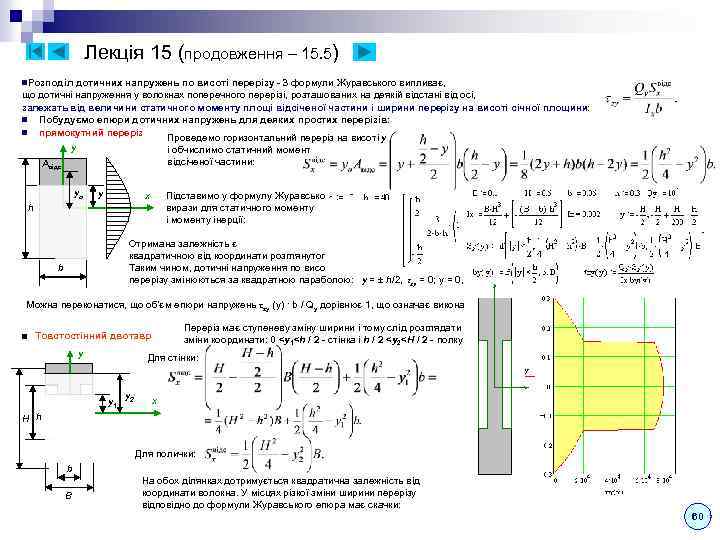Лекція 15 (продовження – 15. 5) n. Розподіл дотичних напружень по висоті перерізу - З формули Журавського випливає, що дотичні напруження у волокнах поперечного перерізі, розташованих на деякій відстані від осі, залежать від величини статичного моменту площі відсіченої частини і ширини перерізу на висоті січної площини: n Побудуємо епюри дотичних напружень для деяких простих перерізів: n прямокутний переріз Проведемо горизонтальний переріз на висоті y y і обчислимо статичний момент відсіченої частини: Aвідс yo y Підставимо у формулу Журавського вирази для статичного моменту інерції: x h Отримана залежність є квадратичною від координати розглянутого шару. Таким чином, дотичні напруження по висоті перерізу змінюються за квадратною параболою: y = h/2, zy = 0; y = 0, zy = zymax =3 Qy/(2 bh) =1, 5 zyср b Можна переконатися, що об’єм епюри напружень τzy (y) · b / Qy дорівнює 1, що означає виконання рівності. Переріз має ступеневу зміну ширини і тому слід розглядати окремо дві ділянки зміни координати: 0

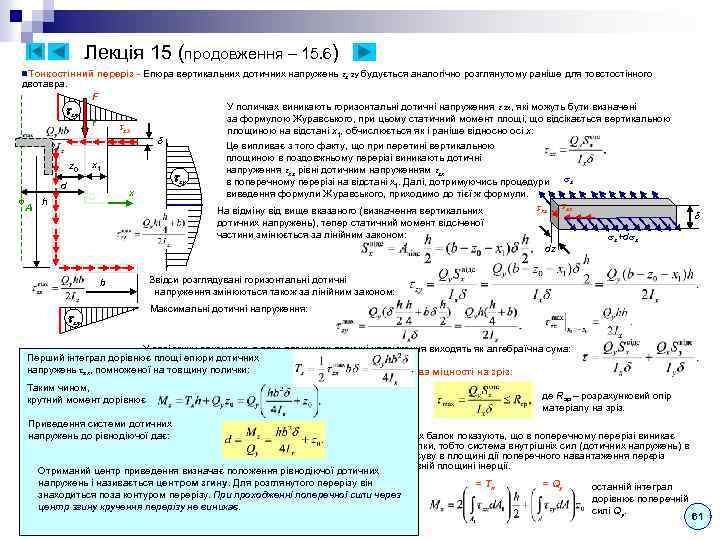Лекція 15 (продовження – 15. 6) n. Тонкостінний двотавра. zx z 0 d A переріз - Епюра вертикальних дотичних напружень z zy будується аналогічно розглянутому раніше для товстостінного F Y zx x 1 zy x С h У поличках виникають горизонтальні дотичні напруження zx, які можуть бути визначені за формулою Журавського, при цьому статичний момент площі, що відсікається вертикальною площиною на відстані x 1, обчислюється як і раніше відносно осі x: Це випливає з того факту, що при перетині вертикальною площиною в поздовжньому перерізі виникають дотичні напруження xz рівні дотичним напруженням zx в поперечному перерізі на відстані x 1. Далі, дотримуючись процедури виведення формули Журавського, приходимо до тієї ж формули. На відміну від вище вказаного (визначення вертикальних дотичних напружень), тепер статичний момент відсіченої частини змінюється за лінійним законом: xz dz b zx z zx z+d z Звідси розглядувані горизонтальні дотичні напруження змінюються також за лінійним законом: Максимальні дотичні напруження: У разі згину одночасно в двох площинах дотичні напруження виходять як алгебраїчна сума: Перший інтеграл дорівнює площі епюри дотичних напружень міцності – Епюри розподілуполички: напружень показують, що Умова міцності на зріз: n Умова τzx, помноженої на товщину дотичних максимальні дотичні напруження виникають на рівні нейтрального шару, де Таким чином, нормальні напруження від дії згинаючого моменту рівні нулю. Тоді міцність де Rзр – розрахунковий опір крутний момент дорівнює балки перевіряється на зріз. матеріалу на зріз. Приведення системи дотичних центр згину - Напрямки дотичних напружень по перерізу тонкостінних балок показують, що в поперечному перерізі виникає рівнодіючої дає: крутний момент відносно центру приведення, що збігається з центральною віссю балки, тобто система внутрішніх сил (дотичних напружень) в перерізі зводиться до головного вектору і головного моменту. Це означає, що крім зсуву в площині дії поперечного навантаження пере різ піддається деформації кручення, хоча поперечне навантаження знаходиться в головній площині інерції. Отриманий центр приведення визначає положення рівнодіючої дотичних Для попередження кручення необхідно змістити площину дії поперечного напружень і називається центром згину. Для розглянутого перерізу він = Tx = Qy останній інтеграл навантаження таким чином, щоб При проходженні поперечної урівноважив знаходиться поза контуром перерізу. крутний момент, що з’явився, сили через дорівнює поперечній момент від дотичних напружень, що рівний: центр згину кручення перерізу не виникає. силі Qy. n. Поняття про напружень до 61

Лекція 15 (продовження – 15. 7) Розрахунки на міцність по дотичним напруженням і зусиллям зсуву - Складені згинальні елементи збираються на основі клейових, зварних, клепаних і болтових з'єднань, що дозволяє створити раціональні перерізи. Ці з'єднання безпосередньо сприймають дотичні зусилля (напруження). ■ Клейові з'єднання - розраховуються на опір зрушенню складових частин. y zymax, 1 де Rкл – розрахунковий опір клею на зріз. умова міцності : n Aвідс x zymax yz z Крім того повинна бути забезпечена міцність на зріз основного матеріалу по найбільших дотичним напруженням на рівні нейтрального шару: де R – розрахунковий опір матеріалу зр на зріз. Якщо матеріал - дерево, міцність якого на сколювання нижче ніж на зріз поперек волокон, то береться розрахунковий опір на сколювання, оскільки τzx = τyz за законом парності дотичних напружень. ■ Зварні з'єднання - розраховуються на міцність зварного шва, що сприймає поздовжнє зсувне зусилля. Y Aвідс Небезпечним перерізом для кутового зварного шва є переріз, що проходить по бісектрисі прямого кута, що відповідає найменшій площі зрізу шва. За розрахунковий переріз приймається Aш = bш ∙ Lш = hш ∙ cos 450 ∙ Lш, де Lш - довжина шва (сегментна частина площі поперечного перерізу шва hш відкидається, як область, в якій не забезпечується якість шва). У загальному випадку приймається Aш = hш ∙ β ∙ Lш, де β - коефіцієнт форми кутового шва, що залежить x При розрахунку на зминання слід вважати, що зсуваюча від виду зварювання (для ручної зварки β=0, 7, напівавтоматичної – β=0, 85, автоматичної – β=1). сила, як рівнодіюча дотичних напружень в площині зсуву, Дотичні напруження, що виникають в розрахунковому перерізі шва, обчислена як для суцільного перерізу, не повинні перевищувати розрахункового опору на зріз матеріалу шва: викликає зминання бічної поверхні заклепок. Розрахунковою площею зминання є найменша з Звідси можна визначити необхідну висоту шва: площ, утвореної перетином діаметральної площиною тіла 2 – кількість швів вузла заклепки. В даному випадку Aзм = dз ∙ δ, де δ - товщина стінки. ■ Заклепкові і болтові з'єднання - розраховуються на зріз і зминання заклепок (болтів), що сприймають Умова міцності на зминання, подібно умові міцності повздовжнє дотичне зусилля. на зріз, приймає вигляд: Нехай крок заклепок, що з'єднують стінку і полку з кутикками однаковий. У цьому випадку, у більш важких умовах працюють заклепки на стінці балки, оскільки статичний момент відсіченої частини для них більше, ніж для заклепок на полиці. x Дотичні напруження, що виникають в поперечному перерізі заклепки, не повинні перевищувати розрахункового опору на зріз матеріалу заклепки (a - крок заклепок, dз - діаметр поперечного перерізу заклепки): Звідси можна визначити необхідний крок заклепок на зминання. Остаточно приймається найменший крок з Звідси можна визначити необхідний крок заклепок: 62 2 – кількість зрізів заклепки визначених за умов зрізу та зминання. Aвідс

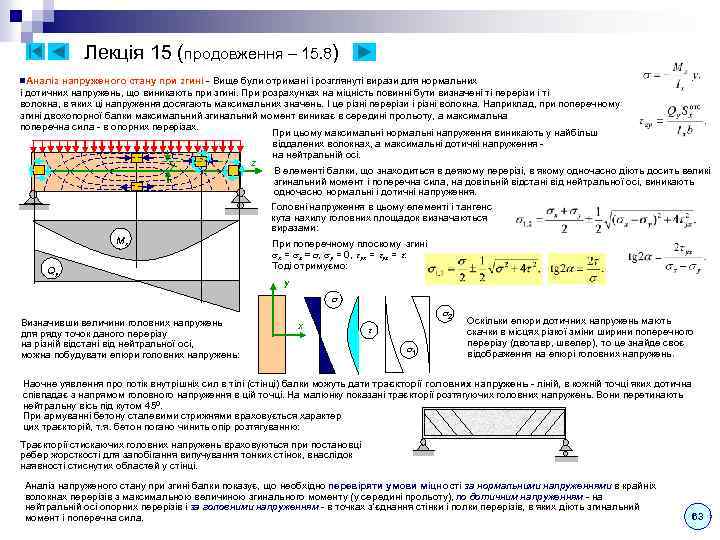Лекція 15 (продовження – 15. 8) n. Аналіз напруженого стану при згині - Вище були отримані і розглянуті вирази для нормальних і дотичних напружень, що виникають при згині. При розрахунках на міцність повинні бути визначені ті перерізи і ті волокна, в яких ці напруження досягають максимальних значень. І це різні перерізи і різні волокна. Наприклад, при поперечному згині двохопорної балки максимальний згинальний момент виникає в середині прольоту, а максимальна поперечна сила - в опорних перерізах. При цьому максимальні нормальні напруження виникають у найбільш віддалених волокнах, а максимальні дотичні напруження на нейтральній осі. z y В елементі балки, що знаходиться в деякому перерізі, в якому одночасно діють досить великі згинальний момент і поперечна сила, на довільній відстані від нейтральної осі, виникають одночасно нормальні і дотичні напруження. Головні напруження в цьому елементі і тангенс кута нахилу головних площадок визначаються виразами: Mx При поперечному плоскому згині x = z = , y = 0, yx = yz = : Тоді отримуємо: Q y y Визначивши величини головних напружень для ряду точок даного перерізу на різній відстані від нейтральної осі, можна побудувати епюри головних напружень: x 2 1 Оскільки епюри дотичних напружень мають скачки в місцях різкої зміни ширини поперечного перерізу (двотавр, швелер), то це знайде своє відображення на епюрі головних напружень. Наочне уявлення про потік внутрішніх сил в тілі (стінці) балки можуть дати траєкторії головних напружень - ліній, в кожній точці яких дотична співпадає з напрямом головного напруження в цій точці. На малюнку показані траєкторії розтягуючих головних напружень. Вони перетинають нейтральну вісь під кутом 450. При армуванні бетону сталевими стрижнями враховується характер цих траєкторій, т. я. бетон погано чинить опір розтягуванню: Траєкторії стискаючих головних напружень враховуються при постановці ребер жорсткості для запобігання випучування тонких стінок, внаслідок наявності стиснутих областей у стінці. Аналіз напруженого стану при згині балки показує, що необхідно перевіряти умови міцності за нормальними напруженнями в крайніх волокнах перерізів з максимальною величиною згинального моменту (у середині прольоту), по дотичним напруженням - на нейтральній осі опорних перерізів і за головними напруженням - в точках з'єднання стінки і полки перерізів, в яких діють згинальний момент і поперечна сила. 63

Лекція 15 (продовження – 15. 9) Згин стрижня в пружнопластичній стадії - Розглянуті раніше умови міцності ґрунтуються на порівнянні максимальних напружень з розрахунковим опором у припущенні пружної роботи матеріалу. Для крихких матеріалів за розрахунковий опір приймається величина, пов'язана з межею міцності, для пластичних - з межею текучості. Для крихких матеріалів виникнення максимальних напружень, більших розрахункового опору, дійсно означає вичерпання несучої здатності аналізованого перерізу і балки вцілому. y σ n Але це не так для матеріалів, що мають стадію текучості. Можна помітити, що у разі згину при досягненні напруженнями в крайніх волокнах граничних значень, волокна, що знаходяться ближче до нейтральної осі, відчувають менші, Напруження, що прямують аж до нуля. x σВ σТ Для цих матеріалів, виникнення напружень, рівних межі текучості, не є граничним станом, оскільки інші волокна ще залишаються пружними і можуть сприймати збільшення навантаження. При збільшенні навантаження зона текучості починає збільшуватися, просуваючись до нейтральної осі. Вичерпання несучої здатності перерізу відбудеться в момент, коли зона текучості пошириться аж до нейтральної осі і матеріал по всьому перерізу буде деформуватися при постійному навантаженні. Стан перерізу, коли у всіх його точках розвиваються пластичні деформації, називають пластичним шарніром. При виникненні пластичного шарніра балка не може залишитися в рівновазі і перетворюється на механізм: При утворенні пластичного шарніра нульова лінія займає положення, що розділяє переріз на дві рівновеликі частини. Це випливає з рівності нулю сумарного поздовжнього зусилля: ε εТ F Розвинутий пластичний шарнір не є ідеальним (здійснює роботу при взаємному повороті суміжних перерізів, тобто надає певний опір). Момент опору повороту суміжних перерізів можна визначити приведенням напружень щодо будь-якої осі, наприклад, центральної (рівнодіюча стискаючих і розтягуючих напружень утворюють пару): Вираз в дужках можна розглядати як пластичний момент опору, проводячи аналогію з моментом опору перерізу в пружній стадії: Пластичний момент опору завжди більше моменту опору перерізу в пружній стадії. Наприклад, для прямокутного перерізу: Таким чином, пластичний момент опору прямокутного перерізу в 1, 5 рази більше пружного, і це означає, що навантаження може бути збільшене в 1, 5 рази з моменту виникнення текучості до повного вичерпання несучої здатності конструкції. 64

Лекція 16 n n ■ Внутрішні зусилля при крученні - При крученні в поперечному перерізі стержня виникає лише один силовий фактор - крутний момент Mz. Відповідно до методу перерізів величина і напрямок крутного моменту може бути знайдені з рівняння рівноваги в моментах щодо осі, що збігається з віссю стрижня, складеного для залишеної частини: Крутний момент вважається позитивним, якщо при погляді на перетин з боку зовнішньої нормалі він повертає перетин по ходу годинникової стрілки. Увага! Це правило знаків умовне і не співпадає з прийнятими правилами знаків моментів, кутів повороту в теоретичній механіці і математиці, оскільки пов'язано не з системою координат, а з видом деформації залишеної частини, точно так, як правило знаків для поздовжнього зусилля пов'язано не з напрямком осі z , а з видом деформації розглянутої частини бруса. Побудова епюри крутних моментів принципово нічим не відрізняється від побудови епюри поздовжніх сил. Позитивні значення відкладаються нагору від горизонтальної базової лінії, а негативні - вниз. z 1 z 2 z 3 III I II Нехай прямолінійний брус навантажений зовнішніми зосередженими крутним моментом M 1, M 2: a MI-I I M 1 b II M 2 III c M 2 M 1 MII-II M 2 MIII-III 1. Реакції лівої опори можна не визначати, тому що в цьому прикладі можна обмежитися Використовуючи отримані вирази для крутного моменту побудуємо епюру крутних моментів: розглядом лише сил, = 250 Нм, M 2 = 100 Нм. Відкладаючичастин (праворуч відзначення крутного моменту Нехай M 1 прикладених до правих залишених на кожній з ділянок перерізів). в Число ділянок - 3 2. деякому вибраному масштабі отримуємо епюру Mz: Зверніть увагу, що стрибки першій ділянці і визначимо поточну координату перерізузовнішніх 3. Проведемо переріз I-I на на епюрі Mz розташовуються в точках прикладення і межі її зосереджених моментів і рівні величинам цих моментів. Відповідно стрибок зміни: 0 z 1 a. на лівому кінці епюри дає величину опорного моменту. 4. Відкинемо ліву частину, замінимо її дію крутним моментом M I-I і складемо рівняння рівноваги в моментах щодо осі z : z З рівняння рівноваги отримуємо вираз для крутного моменту на ділянці 1: Повторюємо кроки 3 та 4 для наступних ділянок: 3. Проведемо переріз II-II на другій ділянці і визначимо поточну координату перерізу і межі її зміни : 0 z 2 b. 4. Відкинемо ліву частину, замінимо її дію крутним моментом Mz. II-II і складемо рівняння рівноваги в моментах щодо осі z : З рівняння рівноваги отримуємо вираз для крутного моменту на ділянці 2: Аналогічно отримуємо для ділянки 3 (0 z 3 c): Отримані вирази показують, що крутний момент в перерізі дорівнює алгебраїчній сумі моментів зовнішніх сил щодо осі бруса, взятих по одну сторону від перерізу! Знак доданків позитивний, якщо розглянутий зовнішній крутний момент обертає перетин за годинниковою стрілкою при погляді на переріз з боку зовнішньої нормалі. 65

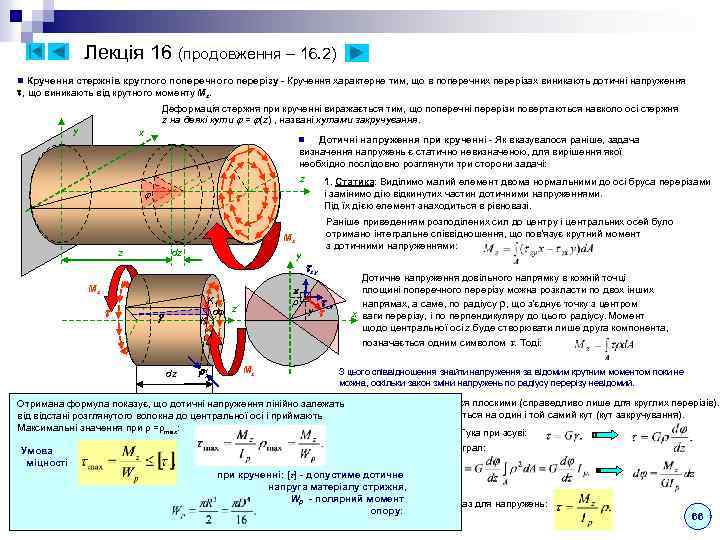Лекція 16 (продовження – 16. 2) Кручення стержнів круглого поперечного перерізу - Кручення характерне тим, що в поперечних перерізах виникають дотичні напруження , що виникають від крутного моменту Mz. n Деформація стержня при крученні виражається тим, що поперечні перерізи повертаються навколо осі стержня z на деякі кути = (z) , названі кутами закручування. y x Дотичні напруження при крученні - Як вказувалося раніше, задача визначення напружень є статично невизначеною, для вирішення якої необхідно послідовно розглянути три сторони задачі: n z 1. Статика: Виділимо малий елемент двома нормальними до осі бруса перерізами і замінимо дію відкинутих частин дотичними напруженнями. Під їх дією елемент знаходиться в рівновазі. Раніше приведенням розподілених сил до центру і центральних осей було отримано інтегральне співвідношення, що пов’язує крутний момент з дотичними напруженнями: Mz dz z Mz y x K 1 dφ z K dz zy Mz y zx Дотичне напруження довільного напрямку в кожній точці площині поперечного перерізу можна розкласти по двох інших напрямах, а саме, по радіусу , що з'єднує точку з центром x ваги перерізу, і по перпендикуляру до цього радіусу. Момент щодо центральної осі z буде створювати лише друга компонента, позначається одним символом . Тоді: З цього співвідношення знайти напруження за відомим крутним моментом поки не можна, оскільки закон зміни напружень по радіусу перерізу невідомий. 2. Отримана формула показує, що дотичні напруження лінійно залежать Геометрія: Відповідно до гіпотези плоских перерізів при своєму повороті перерізи залишаються плоскими (справедливо лише для круглих перерізів). Наступне допущення полягає в тому, центральної осіперерізу залишаються прямими і повертаються на один і той самий кут (кут закручування). відстані розглянутого волокна до що всі радіуси і приймають Максимальні значення при = max: Кут закручування двох суміжних перерізів відрізняється на величину dφ. 3. Фізика: По закону Гука при зсуві: Кут зсуву в будь-якій точці перерізу, що знаходиться на Підставляємо в інтеграл: Умова відстані ρ від центральної осі, рівний відношенню міцності довжини дуги КК 1 до dz: при крученні: [τ] - допустиме дотичне Довжина дуги KK 1: напруга матеріалу стрижня, Wρ - полярний момент Підставляємо у вираз для напружень: опору: 66

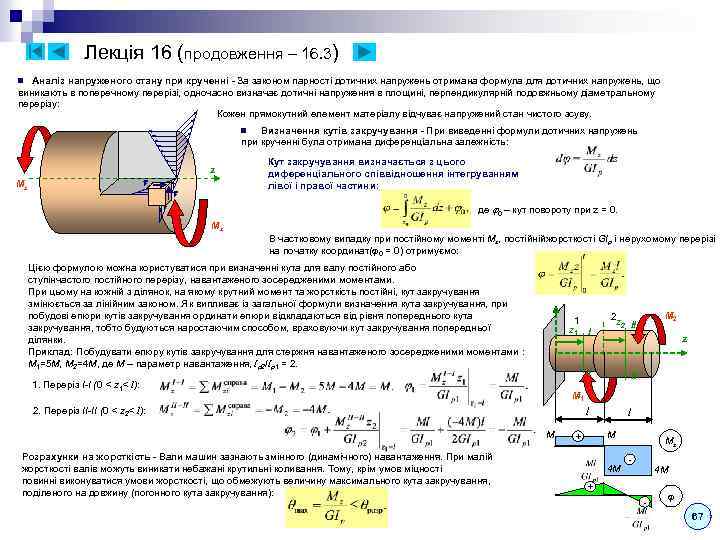Лекція 16 (продовження – 16. 3) Аналіз напруженого стану при крученні - За законом парності дотичних напружень отримана формула для дотичних напружень, що виникають в поперечному перерізі, одночасно визначає дотичні напруження в площині, перпендикулярній подовжньому діаметральному перерізу: Кожен прямокутний елемент матеріалу відчуває напружений стан чистого зсуву. n Визначення кутів закручування - При виведенні формули дотичних напружень при крученні була отримана диференціальна залежність: n Mz z Кут закручування визначається з цього диференціального співвідношення інтегруванням лівої і правої частини: де 0 – кут повороту при z = 0. Mz В частковому випадку при постійному моменті Mz, постійнійжорсткості GIp і нерухомому перерізі на початку координат(φ0 = 0) отримуємо: Цією формулою можна користуватися при визначенні кута для валу постійного або ступінчастого постійного перерізу, навантаженого зосередженими моментами. При цьому на кожній з ділянок, на якому крутний момент та жорсткість постійні, кут закручування змінюється за лінійним законом. Як випливає із загальної формули визначення кута закручування, при побудові епюри кутів закручування ординати епюри відкладаються від рівня попереднього кута закручування, тобто будуються наростаючим способом, враховуючи кут закручування попередньої ділянки. Приклад: Побудувати епюру кутів закручування для стержня навантаженого зосередженими моментами : M 1=5 M, M 2=4 M, де M – параметр навантаження, Ip 2/Ip 1 = 2. 1 z I II l 1. Переріз I-I (0 < z 1< l): l M 1 2. Переріз II-II (0 < z 2< l): M Розрахунки на жорсткість - Вали машин зазнають змінного (динамічного) навантаження. При малій жорсткості валів можуть виникати небажані крутильні коливання. Тому, крім умов міцності повинні виконуватися умови жорсткості, що обмежують величину максимального кута закручування, поділеного на довжину (погонного кута закручування): I M 2 2 z 2 II M + 4 M Mz - 4 M + - φ 67

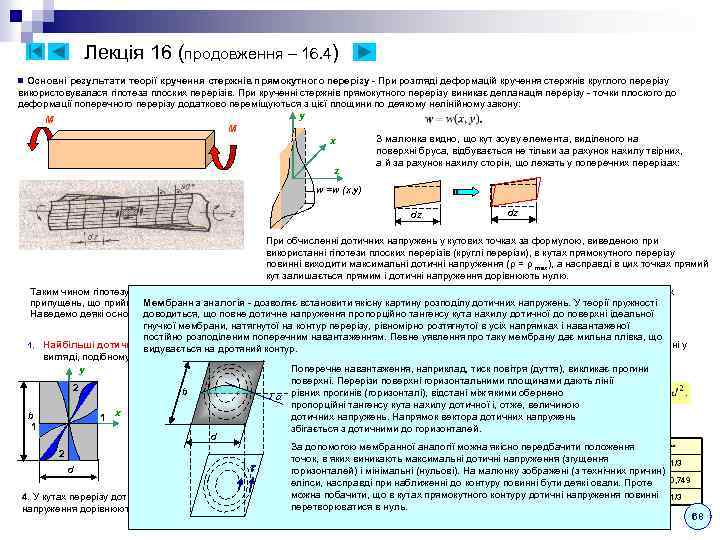Лекція 16 (продовження – 16. 4) Основні результати теорії кручення стержнів прямокутного перерізу - При розгляді деформацій кручення стержнів круглого перерізу використовувалася гіпотеза плоских перерізів. При крученні стержнів прямокутного перерізу виникає депланація перерізу - точки плоского до деформації поперечного перерізу додатково переміщуються з цієї площини по деякому нелінійному закону: y M M З малюнка видно, що кут зсуву елемента, виділеного на x поверхні бруса, відбувається не тільки за рахунок нахилу твірних, а й за рахунок нахилу сторін, що лежать у поперечних перерізах: z n w =w (x, y) dz dz При обчисленні дотичних напружень у кутових точках за формулою, виведеною при використанні гіпотези плоских перерізів (круглі перерізи), в кутах прямокутного перерізу повинні виходити максимальні дотичні напруження (ρ = ρ max), а насправді в цих точках прямий кут залишається прямим і дотичні напруження дорівнюють нулю. Таким чином гіпотезу плоских перерізів неможливо застосувати і задача кручення прямокутного стрижня не може бути вирішена в рамках Мембранна матеріалів. Точне рішення такої якісну розглядається в курсі теорії пружності припущень, що приймаються в опорі аналогія - дозволяє встановити задачі картину розподілу дотичних напружень. У теорії пружності Наведемо деякі основні доводиться, вирішення дотичне напруження пропорційно кручення кута нахилу дотичної до поверхні ідеальної результати що повне методами теорії пружності задачі тангенсу стрижнів прямокутної форми: гнучкої мембрани, натягнутої на контур перерізу, рівномірно розтягнутої в усіх напрямках і навантаженої постійно розподіленим поперечним навантаженням. Певне уявлення про таку мембрану дає мильна плівка, що 1. Найбільші дотичні напруження – виникають уконтур. видувається на дротяний середніх точках (1) довгих сторін прямокутного контуру. Вони можуть бути представлені у вигляді, подібному у раніш отриманій формулі: Тут момент опору при крученні обчислюється Поперечне навантаження, наприклад, тиск повітря (дуття), викликає прогини y за допомогою табличного коефіцієнта, що залежить поверхні. Перерізи поверхні горизонтальними площинами дають лінії від співвідношення довжин сторін (b / d): 2 b рівних прогинів (горизонталі), відстані між якими обернено 2. У середніх точках (2) коротких сторін прямокутного контуру, виникають дещо менші дотичні пропорційні тангенсу кута нахилу дотичної і, отже, величиною x напруження. Вони визначаються дотичних напружень. Напрямок вектора дотичних напружень через максимальні виразом: b 1 1 збігається з дотичними до горизонталей. 3. Кут закручування d Визначається виразом: b/d 1, 5 1, 75 2 2, 5 3 6 10 ∞ За допомогою1 мембранної аналогії можна якісно передбачити положення 2 точок, в яких виникають максимальні дотичні напруження (згущення d 4. У кутах перерізу дотичні напруження дорівнюють нулю. де k 1 0, 208 0, 231 0, 239 0, 246 0, 258 0, 267 0, 299 0, 313 горизонталей) і мінімальні (нульові). На малюнку зображені (з технічних причин) k 2 1 0, 859 0, 820 0, 795 0, 766 0, 753 0, 742 еліпси, насправді при наближенні до контуру повинні бути деякі овали. Проте можна побачити, що в 0, 156 прямокутного контуру дотичні напруження повинні кутах 0, 214 k 3 0, 141 0, 229 0, 249 0, 263 0, 299 0, 313 перетворюватися в нуль. 1/3 0, 749 1/3 68

Лекція 17 n Розрахунок циліндричних гвинтових пружин з малим кутом нахилу - умова міцності. Якщо пружина із тонкої проволки має досить великий діаметр в порівнянні із товщиною дроту, то добавкою за рахунок сил зсуву нехтують і максимальне дотичне напруження: 69

Лекція 17 (продовження – 17. 2) - усадка пружини. - умова жорсткості. 70

Лекція 18 n n RA Статично невизначені системи при розтязі-стиску. У статично невизначених системах число накладених зв'язків більше числа незалежних рівнянь рівноваги. Як зазначалося вище, такі завдання вирішуються послідовним розглядом статичної, геометричної і фізичної сторін, в результаті чого виходить повна система рівнянь, що дозволяє знайти шукані зусилля. Загальний порядок вирішення визначається вищесказаним, конкретні кроки і особливості розглянемо на прикладах: Приклад 1. Стержень змінного перерізу (2 A і A) жорстко закріплений з двох сторін і навантажений поздовжньою силою. Побудувати епюри N та σ. z 1. Вибираємо об'єкт рівноваги, відкидаємо зв'язки і замінюємо їх дію реакціями: B RB F A 2. Статика : Складаємо рівняння рівноваги : a a a B RB F A a Це єдине рівняння рівноваги, яке можна скласти для лінійної системи сил. Отже система один раз статично невизначена. 3. Геометрія: z Складаємо рівняння сумісності деформацій : Це рівняння встановлює незмінність загальної довжини стержня при будь-яких діях, яку забезпечували зв'язки (жорсткі закріплення) до їх видалення. 4. Фізика: Записуємо співвідношення зв'язку деформацій з зусиллями : a a 0, 75 F + N - 0, 375 F/A 0, 25 F + - Отримали повну систему рівнянь, що вирішує дану задачу (5 рівнянь та 5 невідомих - 2 реакції і 3 переміщення). Підставляємо співвідношення пружності в рівняння сумісності: 0, 25 F/A - σ Підставимо отримане співвідношення в рівняння рівноваги: Такий же результат можна отримати з використанням статично визначеної Складаємо рівняння сумісності деформацій : Після визначення з заданої статично невизначеної відкиданням системи, утвореноїопорних реакцій можна побудувати або епюру поздовжніх сил обчисленням значень по ділянках : “зайвого" зв'язку, та принципу незалежності дії сил: N 1 = RA = 3 F/4, Це рівняння встановлює незмінність загальної довжини, яку забезпечував зайвий зв’язок (праве жорстке закріплення) до її видалення, або Якщо був наявний початковий зазор, наприклад між правим кінцем N 2 = N 3 переміщень рівність = RB = F/4. та їх протилежний напрямок при окремій дії зовнішнього навантаження та реакції цього зв’язку. стержня і закріпленням, або навпаки натяг (початковий розмір стержня У перерізі, в якому прикладена зосереджена сила, перевищував відстань між опорами), то це враховується лише Записуємо відношення зв’язку деформацій отримали стрибок, що дорівнює величині цієї сили. в рівняннях сумісності деформацій : (переміщень) із також будується Епюра нормальних напруженьзусиллями: або ( >0 зазор, <0 натяг) обчисленням значень напружень по ділянках : Отримали повну систему рівнянь, що вирішує дану задачу (4 Підставимо до нього, співвідношення σ1 = N 1 / A = 3 F/8 A, Якщо замість силового навантаження, або додатково отримане діє рівняння та 4 1 невідомих – 2 реакції та 2 переміщення). у враховується введенням σ2 = N 2 / A 2= F/8 A, температурне навантаження (нагрів), то це рівняння рівноваги та отримаємо Підставляючи переміщення у рівняння сумісності: величину іншої опорної реакції (RB). 71 σ3 = N 3 / A 3= F/4 A. температурних видовжень в рівняння спільності деформацій. У перерізі різкої зміни площі отримали стрибок. 0, 125 F/A

Лекція 18 (продовження – 18. 2) Розрахунок статично невизначених систем на дію температури – У статично невизначених системах нагрівання (охолодження) елементів викликає додаткові внутрішні зусилля (напруження), які можуть значно перевищувати зусилля від дії силового навантаження. Загальний порядок вирішення завдання зберігається, але рівняння сумісності деформацій (видовжень) містять видовження від дії різниці температур t : - коефіцієнт лінійного розширення матеріалу, l - довжина стрижня. n Приклад 2. Стержень змінного перерізу (2 A і A), розглянутий у прикладі 1, додатково нагрівається на t градусів. t 1. Вибираємо об'єкт рівноваги, відкидаємо зв'язки і замінюємо їх дію реакціями: B RB RA F A 2. Статика : Складаємо рівняння рівноваги: 3. Геометрія: Складаємо рівняння сумісності деформацій : a a a n z Це рівняння встановлює незмінність загальної довжини стержня при будь-яких діях, у тому числі від нагріву, яку забезпечували зв'язки (жорсткі закріплення) до їх видалення. 4. Фізика: Записуємо співвідношення зв'язку деформацій з зусиллями і температурних впливом : Підставляємо співвідношення пружності і температурного видовження в рівняння сумісності: Підставимо отримане співвідношення в рівняння рівноваги: Тепер, при температурному впливі, у вирази для реакцій входять абсолютні значення модуля пружності E і площі A. Обчислимо величини реакцій для конкретних даних: F = 10 к. Н, A = 1 см 2, t = 10 o, E = 2*105 МПа, =10 -5 (сталь): При відсутності нагріву реакції виходять рівними -2. 5 КН і 7. 5 к. Н відповідно. Епюру поздовжніх сил будуємо обчисленням значень по ділянках : N 1 = RA = 4. 5 к. Н, N 2 = N 3 = RB = -5. 5 к. Н. У перерізі, в якому прикладена зосереджена сила, отримано стрибок, що дорівнює величині цієї сили. Епюра нормальних напружень також будується обчисленням значень напруг по ділянках: σ1 = N 1 / A 1= 22. 5 МПа, σ2 = N 2 / A 2= - 27. 5 МПа, σ3 = N 3 / A 3= - 55 МПа. При відсутності нагріву значення напружень виходять рівними 37. 5 МПа, - 12. 5 МПа, і -25 МПа відповідно (вид епюри напружень див. у прикладі 1). Таким чином, нагрів всього на 10 о привів до збільшення стискаючої сили і максимальних стискаючих напружень більше, ніж в 2 рази. Статично невизначені системи завжди реагують на зміну температури зміною внутрішніх зусиль. Це ж відбувається при взаємних зсувах опор (нерівномірне осідання опор). 72

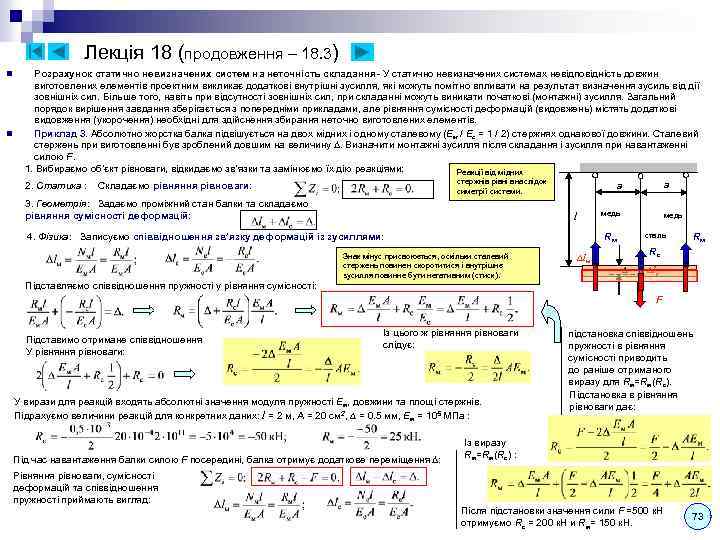Лекція 18 (продовження – 18. 3) n n Розрахунок статично невизначених систем на неточність складання - У статично невизначених системах невідповідність довжин виготовлених елементів проектним викликає додаткові внутрішні зусилля, які можуть помітно впливати на результат визначення зусиль від дії зовнішніх сил. Більше того, навіть при відсутності зовнішніх сил, при складанні можуть виникати початкові (монтажні) зусилля. Загальний порядок вирішення завдання зберігається з попередніми прикладами, але рівняння сумісності деформацій (видовжень) містять додаткові видовження (укорочення) необхідні для здійснення збирання неточно виготовлених елементів. Приклад 3. Абсолютно жорстка балка підвішується на двох мідних і одному сталевому (Eм / Eс = 1 / 2) стержнях однакової довжини. Сталевий стержень при виготовленні був зроблений довшим на величину Δ. Визначити монтажні зусилля після складання і зусилля при навантаженні силою F. 1. Вибираємо об’єкт рівноваги, відкидаємо зв’язки та замінюємо їх дію реакціями: Реакції від мідних 2. Статика : стержнів рівні внаслідок симетрії системи. Складаємо рівняння рівноваги: 3. Геометрія: Задаємо проміжний стан балки та складаємо рівняння сумісності деформацій: l 4. Фізика: Записуємо співвідношення зв’язку деформацій із зусиллями: медь сталь Rм Знак мінус присвоюється, оскільки сталевий стержень повинен скоротитися і внутрішнє зусилля повинне бути негативним (стиск). a a lм Rм Rс lс Підставляємо співвідношення пружності у рівняння сумісності: F Підставимо отримане співвідношення У рівняння рівноваги: Із цього ж рівняння рівноваги слідує: У вирази для реакцій входять абсолютні значення модуля пружності Eм, довжини та площі стержнів. Підрахуємо величини реакцій для конкретних даних: l = 2 м, A = 20 см 2, = 0. 5 мм, Eм = 105 МПа : Під час навантаження балки силою F посередині, балка отримує додаткове переміщення Δ: підстановка співвідношень пружності в рівняння сумісності приводить до раніше отриманого виразу для Rм=Rм(Rс). Підстановка в рівняння рівноваги дає: Із виразу Rм=Rм(Rс) : Рівняння рівноваги, сумісності деформацій та співвідношення пружності приймають вигляд: Після підстановки значення сили F =500 к. Н отримуємо Rс = 200 к. Н и Rм= 150 к. Н. 73

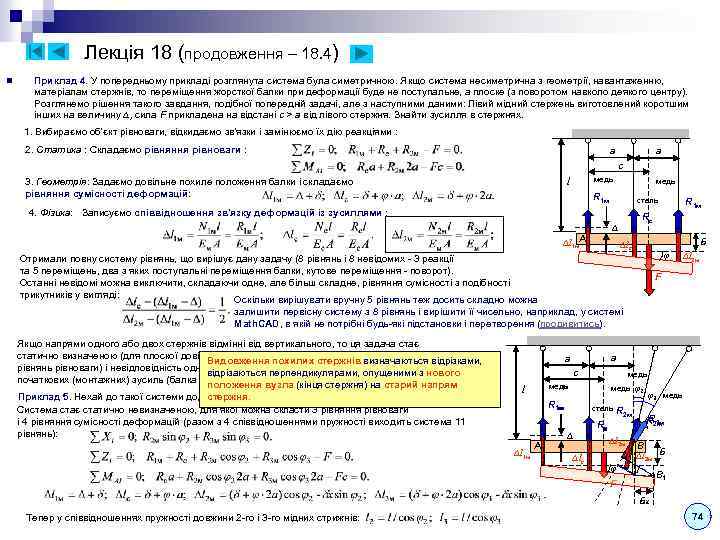Лекція 18 (продовження – 18. 4) n Приклад 4. У попередньому прикладі розглянута система була симетричною. Якщо система несиметрична з геометрії, навантаженню, матеріалам стержнів, то переміщення жорсткої балки при деформації буде не поступальне, а плоске (з поворотом навколо деякого центру). Розглянемо рішення такого завдання, подібної попередній задачі, але з наступними даними: Лівий мідний стержень виготовлений коротшим інших на величину , сила F прикладена на відстані c > a від лівого стержня. Знайти зусилля в стержнях. 1. Вибираємо об'єкт рівноваги, відкидаємо зв'язки і замінюємо їх дію реакціями : 2. Статика : Складаємо рівняння рівноваги : a a с медь l 3. Геометрія: Задаємо довільне похиле положення балки і складаємо рівняння сумісності деформацій: медь R 1 м сталь 4. Фізика: Записуємо співвідношення зв'язку деформацій із зусиллями : Rс l 1 м. А R 1 м б lс φ Отримали повну систему рівнянь, що вирішує дану задачу (8 рівнянь і 8 невідомих - 3 реакції та 5 переміщень, два з яких поступальні переміщення балки, кутове переміщення - поворот). Останні невідомі можна виключити, складаючи одне, але більш складне, рівняння сумісності з подібності трикутників у вигляді: Оскільки вирішувати вручну 5 рівнянь теж досить складно можна l 2 м F залишити первісну систему з 8 рівнянь і вирішити її чисельно, наприклад, у системі Math. CAD, в якій не потрібні будь-які підстановки і перетворення (продивитись). Якщо напрями одного або двох стержнів відмінні від вертикального, то ця задача стає статично визначеною (для плоскої довільної системи сил можна скласти 3 незалежних Видовження похилих стержнів визначаються відрізками, рівнянь рівноваги) і невідповідність одного або двох розмірів проектним не викликатимуть відрізаються перпендикулярами, опущеними з нового початкових (монтажних) зусиль (балка лише змінить свій стан при збірці). положення вузла (кінця стержня) на старий напрям Приклад 5. Нехай до такої системи доданий ще один "зайвий" стрижень). стержня. Система стає статично невизначеною, для якої можна скласти 3 рівняння рівноваги і 4 рівняння сумісності деформацій (разом з 4 співвідношеннями пружності виходить система 11 рівнянь): a a с l медь φ2 R 1 м l 1 м медь А сталь lс R 2 м Rс l 2 м φ φ3 медь R 3 м R 2 м B l 3 м б B 1 F бx Тепер у співвідношеннях пружності довжини 2 -го і 3 -го мідних стрижнів: 74

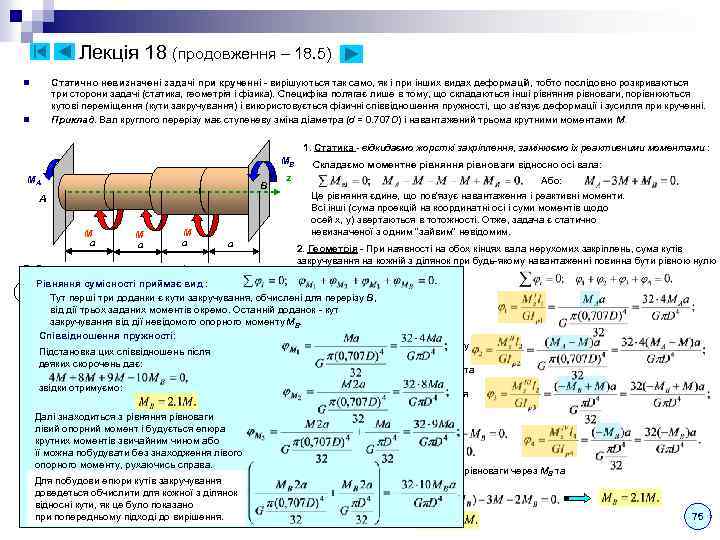Лекція 18 (продовження – 18. 5) Статично невизначені задачі при крученні - вирішуються так само, як і при інших видах деформацій, тобто послідовно розкриваються три сторони задачі (статика, геометрія і фізика). Специфіка полягає лише в тому, що складаються інші рівняння рівноваги, порівнюються кутові переміщення (кути закручування) і використовується фізичні співвідношення пружності, що зв'язує деформації і зусилля при крученні. Приклад. Вал круглого перерізу має ступеневу зміна діаметра (d = 0. 707 D) і навантажений трьома крутними моментами M. n n 1. Статика - відкидаємо жорсткі закріплення, замінюємо їх реактивними моментами : MB MA B A M a M a Побудуємо епюру крутних моментів: a z Складаємо моментне рівняння рівноваги відносно осі вала: Або: Це рівняння єдине, що пов'язує навантаження і реактивні моменти. Всі інші (сума проекцій на координатні осі і суми моментів щодо осей x, y) звертаються в тотожності. Отже, задача є статично невизначеної з одним "зайвим" невідомим. 2. Геометрія - При наявності на обох кінцях вала нерухомих закріплень, сума кутів закручування на кожній з ділянок при будь-якому навантаженні повинна бути рівною нулю - Рівняння сумісності деформацій): 0, 9 M Рівняння сумісності приймає вид : 0, 9 M + 3. Фізика – на кожній Тут перші три доданки є кути закручування, обчислені для перерізу B, з ділянок кут закручування пов’язаний з 0, 1 M від дії трьох заданих моментів окремо. Останній доданок - кут крутним моментом в перерізі закручування від дії невідомого опорного моменту MB. 1, 1 M (співвідношення пружності): Співвідношення пружності: Отримані 6 рівнянь утворюють повну Побудуємо епюру кутів закручування: 2, 1 M Підстановка цих співвідношень після систему рівнянь із шістьма деяких скорочень φ2= -0, 1 Ma/(GIp 1) дає: невідомими (2 реактивних моменти та φ1=0, 9 Ma/(GIp 1) φ3= -0, 275 Ma/(GIp 1) 4 кута закручування). Підставимо звідки отримуємо: φ3= -0, 525 Ma/(GIp 1)співвідношення пружності у рівняння сумісності. Однакові співмножники + Далі знаходиться з рівняння рівноваги винесемо за дужки та скоротимо: лівий опорний момент і будується епюра 0 + 0 крутних моментів звичайним чином або φ1 побудувати без φ1 +φ2 +φ3 = 0, 525 Ma/(GIp 1) Або: її можна+φ2 = 0, 8 Ma/(GIp 1) знаходження лівого опорного моменту, рухаючись справа. Виразимо, наприклад МА із рівняння рівноваги через МВ та Цю задачу можна вирішити інакше, використовуючи у Для побудови епюри статично визначену систему, підставимо в отримане рівняння: якості основної системи кутів закручування длядоведеться обчислити для кожної з ділянок якої можна знайти кути закручування із відносні кути, як це було показано використанням принципу незалежності дії сил від при попередньому підході до вирішення. заданих моментів та невідомого опорного моменту: Mz 75