Полнота непротиворечивость и независимость системы аксиом исчисления высказываний

Полнота, непротиворечивость и независимость системы аксиом исчисления высказываний

Доказуемость формулы и ее тождественная истинность В основе исчисления высказываний лежат абстрактные понятия синтаксиса: лишенные смысла знаки и формальные действия с ними алфавит, аксиома, формула, правило вывода, доказательство, теорема. Эти понятия называются синтаксическими. Алгебра высказываний пронизана содержательным смыслом: за каждой переменной стоит простое высказывание нашего языка, каждая формула может превращаться в составное высказывание истинное или ложное. Такие понятия считаются семантическими понятиями.

Связь исчисления высказываний и алгебры высказываний Формализованное исчисление высказываний построено так, что всякая его теорема является тавтологией алгебры высказываний. Обратно, для всякой тавтологии алгебры высказываний можно построить ее вывод из аксиом формализованного исчисления высказываний, то есть доказать, что она является теоремой исчисления высказываний.

Полнота исчисления высказываний состоит в совпадении множества доказуемых формул, выводимых из системы аксиом с множеством тавтологий алгебры высказываний. Теорема 1. Всякая теорема исчисления высказываний является ТИ формулой алгебры высказываний ( F |= F). Доказательство. Легко проверить, что аксиомы A 1 A 3 являются ТИ формулами. Также легко проверить, что формула, получаемая по правилу MP из ТИ формул сама является ТИ формулой. Теорема 2. Всякая ТИ формула алгебры высказываний доказуема в исчислении высказываний. Символически: |=F F.

Теорема о полноте исчисления высказываний Объединяя теоремы 1 и 2, получаем теорему о полноте (формализованного исчисления высказываний). Теорема. Формула тогда и только тогда доказуема в исчислении высказываний (является теоремой), когда она является тавтологией алгебры высказываний. Символическая запись: | F = F.

Непротиворечивость аксиоматической теории Аксиоматическая теория называется непротиворечивой, если ни для какого утверждения А, сформулированного в терминах этой теории, само утверждение А и его отрицание не могут быть одновременно теоремами данной теории. В противном случае теория называется противоречивой. Противоречивая теория ценности не имеет.

Непротиворечивость исчисления высказываний Теорема: формализованное исчисление высказываний есть непротиворечивая аксиоматическая теория. Доказательство: допустим противное, то есть пусть исчисление высказываний противоречиво. Значит имеется такая формула F, что F и являются теоремами исчисления высказываний. Тогда по теореме о полноте каждая из этих формул является тавтологией в алгебре высказываний. Но это невозможно на основание определения тавтологии. Следовательно, исчисление высказываний непротиворечиво.

Понятие о независимости системы аксиом После изучения исчисления высказываний могут возникнуть вопросы. Почему в качестве аксиом взята система из трех аксиом S = {A 1, A 2, A 3} ? Нельзя ли сократить число аксиом до двух, не теряя свойства полноты исчисления высказываний? Определение: аксиома A из системы аксиом S называется независящей от остальных аксиом этой системы, если ее нельзя вывести (доказать) из множества аксиом S {A}. Определение: система аксиом S называется независимой, если любая ее аксиома не зависит от остальных.

Теорема о независимости системы аксиом {A 1, A 2, A 3} Теорема: система аксиом {A 1, A 2, A 3} исчисления высказываний независима. Для доказательства независимости аксиомы от остальных, нужно построить модель системы аксиом, в которой выполнялись бы все аксиомы кроме той, независимость которой доказывается. При этом модель нужно выбрать так, чтобы выбранные объекты и отношения между ними обладали бы свойствами, сформулированными для аксиом из системы S {A} и не обладали бы свойством A. Наличие такой модели доказывает независимость аксиомы A от аксиом из множества S {A}.

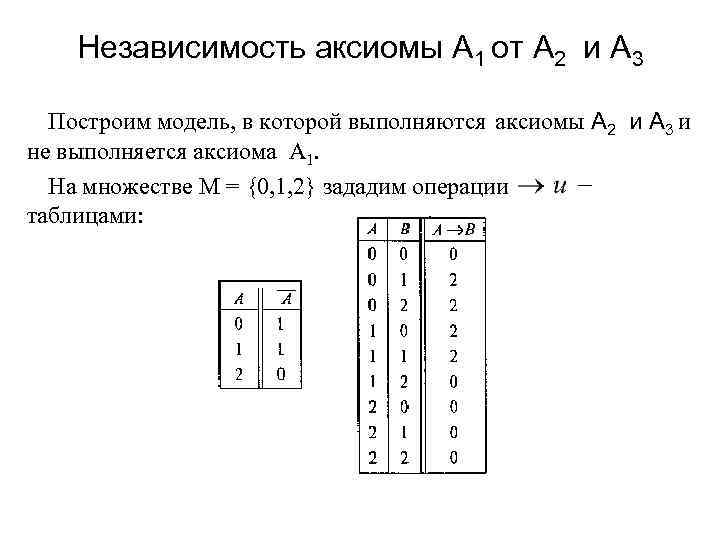Независимость аксиомы A 1 от A 2 и A 3 Построим модель, в которой выполняются аксиомы A 2 и A 3 и не выполняется аксиома A 1. На множестве M = {0, 1, 2} зададим операции таблицами:

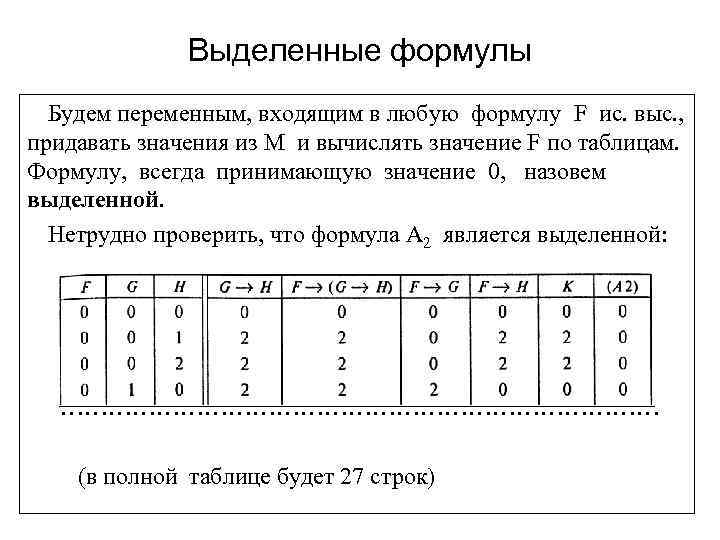Выделенные формулы Будем переменным, входящим в любую формулу F ис. выс. , придавать значения из M и вычислять значение F по таблицам. Формулу, всегда принимающую значение 0, назовем выделенной. Нетрудно проверить, что формула A 2 является выделенной: ………………………………… (в полной таблице будет 27 строк)

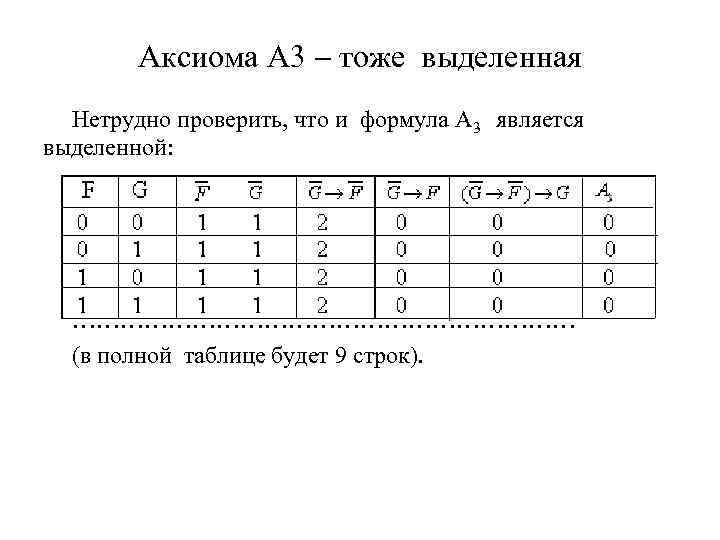Аксиома A 3 тоже выделенная Нетрудно проверить, что и формула A 3 является выделенной: …………………………… (в полной таблице будет 9 строк).

Правило MP сохраняет свойство выделенности В таблице, определяющей операцию над элементами множества {0, 1, 2} формулы A и A B принимают значение 0 только в первой строке. Но в этой строке B тоже принимает значение 0. Это означает, что правило MP сохраняет свойство выделенности. Из доказанных утверждений следует, что любая формула полученная из аксиом A 2 и A 3 с помощью правила MP является выделенной

Аксиома A 1 не выводима из A 2 и A 3 Аксиома A 1 не является выделенной. Если формула F принимает значение 1, а формула G имеет значение 2, то Модель, в которой выполняются аксиомы A 2 и A 3 и не выполняется аксиома A 1 построена. Значит Аксиома A 1 не зависит от аксиом A 2 и A 3. Аналогично доказывается независимость аксиом A 2 и A 3.

Теоремы К. Геделя (1906 -78) о неполноте Аксиоматический метод обладает многими достоинствами и с успехом применяется на практике для формализации разнообразных предметных областей в математике, физике и других науках. Однако этому методу присуще следующее принципиальное ограничение: Теорема 1 Геделя. Во всякой достаточно богатой теории (в частности, включающей формальную арифметику) существует такая истинная формула F, что ни F, ни не являются выводимыми в этой теории. Теорема 2 Геделя. Во всякой достаточно богатой теории (в частности, включающей формальную арифметику) формула F, утверждающая непротиворечивость этой теории не является выводимой в ней.

Вторая теорема Геделя не утверждает, что формальная арифметика противоречива. Она утверждает, что непротиворечивость достаточно богатой формальной теории не может быть установлена средствами самой этой теории. Возможно, непротиворечивость конкретной теории можно установить средствами другой, более мощной формальной теории. Но тогда возникает вопрос о непротиворечивости этой второй теории и так далее.