Поле комплексных чисел Выполнила: Рыбникова Екатерина Группа БУ-14
Комплексными числами называются упорядоченные пары действительных чисел вида , для которых операции сложения и умножения вводятся в соответствии со следующими аксиомами: 1. Два комплексных числа и считаются равными в том и только в том случае, если и , что при помощи логической символики записывается так: 2
2. Сумма двух комплексных чисел и является комплексным числом, которое находится по правилу: 3. Произведение двух комплексных чисел и является комплексным числом, которое находится по правилу: 3
4. Комплексное число отождествляется с действительным (вещественным) числом В частности, Число вида числами. называются мнимыми 4
Операции сложения и умножения комплексных чисел коммутативны и ассоциативны. Обозначим Коммутативность операций сложения и умножения комплексных чисел непосредственно следует из сравнения правых частей приведенных ниже равенств с учетом коммутативности операций сложения и умножения действительных чисел и аксиом 2 и 3: 5
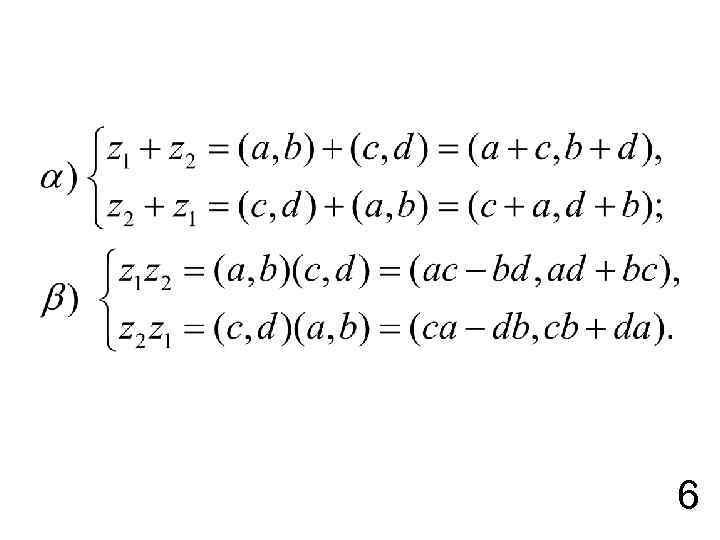
6
Ассоциативность операций сложения и умножения комплексных чисел также следует из свойств соответствующих операций над действительными числами, аксиом 2 и 3 и сравнения правых частей следующих неравенств: 7
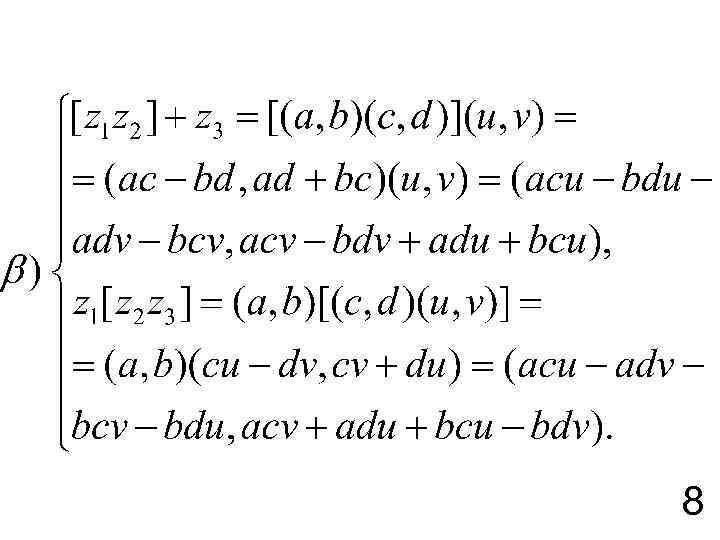
8
Операции умножения и сложения комплексных чисел связаны с дистрибутивными законами, справедливость которых вытекает из аксиомы 1 и следующих равенств: 9
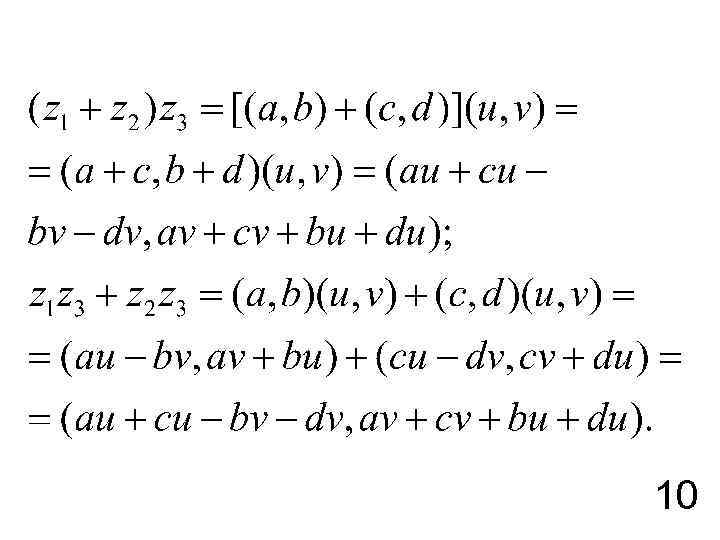
10
Разностью двух комплексных чисел называется такое комплексное число , что Частным комплексных чисел называется такое комплексное число , что 11
Алгебраическая форма комплексных чисел Рассмотрим следующую выкладку: Из которой в соответствии с аксиомой 4, постулирующей отождествление комплексных чисел вида с вещественными числами, и обозначением для мнимой единицы вытекает следующая форма записи комплексных чисел: 12
которая называется алгебраической формой комплексных чисел. Вещественное число называется вещественной частью комплексного числа и обозначается еще а вещественное число называется мнимой частью комплексного числа и обозначается Число вида называется комплексносопряженным к числу и обозначается 13
Декартова плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс на комплексной плоскости называется вещественной осью, а ось ординат – мнимой осью. Модулем комплексного числа называется длина радиуса – вектора точки на комплексной плоскости. Аргументом комплексного числа называется полярный угол точки, изображающей это число 14
Модуль комплексного числа обозначается , аргумент комплексного числа обозначается. Аргумент комплексного числа не имеет смысла. Положительным направлением отсчета аргумента комплексного числа считается направление от положительной полуоси вещественной оси к положительной полуоси мнимой оси, то есть против часовой стрелки. 15
Все возможные значения аргумента комплексного числа даются формулой: где - аргумент комплексного числа многозначен. Справедливы формулы: Откуда для комплексного числа получаем тригонометрическую форму записи: 16
Теорема 1. Для модуля суммы и разности двух комплексных чисел имеют место равенства: 1. 2. 3. 4. 17
Теорема 2. Корнем n-й степени из комплексного числа называется такое комплексное число (или числа) , что справедливо равенство Корни n-й степени из комплексного числа существуют и все они даются формулой при любом целом числе 18
Следствие из теоремы 2. Существуют ровно различных значений корня n-ой степени из комплексного числа , которые вычисляются по формуле (1) при 19
Скачать презентацию Поле комплексных чисел Выполнила Рыбникова Екатерина Группа БУ-14
Pole_komplexnykh_chisel.pptx