7c85a329dbd40d1167a4e14857e89fec.ppt
- Количество слайдов: 26

Polarimetry II Bob Sault 26 September 2012
Polarized light RAS 2012: Polarimetry II

Outline • Preliminaries • Stokes parameters; feeds; imaging • Nuts and bolts • Formalism; depolarization; calibration; feeds (again) • Advanced • More formalism; calibration requirements; off-axis response RAS 2012: Polarimetry II

How to describe polarized light • Polarized state of light can be described by 4 parameters e. g. • Total power; • Fractional powers in horizontal and vertical linear components; • Phase relationship between the horizontal and vertical components. RAS 2012: Polarimetry II

Stokes parameters • I – total power – the sum of the power in any two orthogonal components … • Q – difference in power between the vertical and horizontal components: • U – difference between ± 45 o components. • V – difference between circularly polarized components. RAS 2012: Polarimetry II

Feeds • Linearly-polarized feeds. Dipoles. • “Vertical” and “horizontal” - “X” and “Y” (note X is vertical, Y is horizontal) • Circularly-polarized feeds. Helical feeds. • “Right handed” and “left handed” • Quadrature hybrids. • Combiner/phasing networks to convert linear feeds to circular response. RAS 2012: Polarimetry II

Measurement of Stokes parameters • Conceptually use many feeds to measure the different orthogonal polarizations … • At radio frequencies voltages can be measured and correlated! where XX is and XY is RAS 2012: Polarimetry II and YY is and YX is (“parallel hand” correlations) (“cross hand” correlations).

Making Stokes images • Each antenna measures two orthogonal polarizations - X and Y. • For every baseline, form all four possible correlations - XX, YY, XY, YX. • Calibration and other tricks • Appropriately combine the four correlations to get four Stokes “visibilities”. • Perform standard imaging with these Stokes visibilities to make Stokes images. RAS 2012: Polarimetry II

Jones matrices • The response of an optical component to polarized light can described by a simple linear operation on the voltages: or more simply, in matrix form for a complex system, the overall Jones matrix will be the product of several matrices: RAS 2012: Polarimetry II

Jones matrices continued … • Jones matrices are “antenna based” • Antenna gain: • Polarization leakage: • Rotation: RAS 2012: Polarimetry II

Polarization leakage • For real-world feeds, the feed will respond both to the desired polarization, and to a small degree the orthogonal polarization: The leakage (“d term”) is typically ~10 -2. It is caused by alignment error, feed ellipticity, etc. Generic linear model (will suit practically anything). RAS 2012: Polarimetry II

Rotation RAS 2012: Polarimetry II

Rotation • Alt-az mount For a conventional alt-az mount, the sky rotates relative to the antenna feed - ``parallactic angle rotation’’ • Instrumental polarization (leakage) will be in the frame of the antenna • Astronomical polarization will be in the frame of the sky. • Instrumental and astronomical characteristics can be decoupled if the your observation spans a good range of parallactic angles. • Equatorial and “sky” mounts, parallactifiers RAS 2012: Polarimetry II

On-line calibration (ATCA) Generally there is little (or no!) signal in cross -hand correlations, so relative phase and delay of X and Y channels are difficult to set astronomically. → Noise source calibration RAS 2012: Polarimetry II

Off-line calibration (ATCA) • Determine leakage terms. • To first order, simple regular observation of “typical” calibrator is all that is needed. • Stokes parameters of calibrator either • Must be known and accounted for, or • Decoupled, using “parallactic angle rotation”, from instrumental polarization RAS 2012: Polarimetry II

Depolarization • Depolarization = loss of polarimetric signal. • Caused by the system polarimetric response not being constant (i. e. varying spatially, with time, across bandwidth etc) smearing out the polarimetric signal. • Calibrated interferometers generally have very low depolarization (in polarimetric jargon, a system with no depolarization is called “pure”). RAS 2012: Polarimetry II

Feeds • Some debate on whether linearly (e. g. ATCA, ASKAP, WSRT, KAT) or circularly polarized feeds (e. g. VLA) are “best”. • Linear feeds easier to engineer, better wideband performance. • Circular feeds have advantages for singlefeed (non-polarimetric) systems. • Linear feeds Û circular polarized sources • Circular feeds Û linearly polarized sources RAS 2012: Polarimetry II

Outline • Preliminaries • Stokes parameters; feeds; imaging • Nuts and bolts • Formalism; depolarization; calibration; feeds (again) • Advanced • More formalism; calibration requirements; off-axis response RAS 2012: Polarimetry II

More formalism • Jones matrices describe “pure” systems (systems without depolarization). A more general formalism – Mueller matrices - exists for systems with depolarization. ØLess relevant for interferometers because they are generally “pure” after calibration. ØMay be useful for single dish telescopes. ØMueller and Jones matrices can be a powerful way to analyse complex polarimetric systems. RAS 2012: Polarimetry II

Mueller matrices Muller matrices are of size 4 x 4 and relate output Stokes parameters to inputs: or For pure systems, a Mueller matrix has an associated Jones matrix RAS 2012: Polarimetry II

Advanced calibration • Polarimetric calibration converts an interferometer into a “pure” system. There are 7 parameters that are potentially illdetermined. RAS 2012: Polarimetry II

Advanced calibration … • “Standard” calibration removes leakage of Stokes I into Q, U, V. It does not calibrate out leakage of Q, U, V into each other. These leakages are second-order and often not important. • Formally three independent “observations” of known calibrators are needed to fully solve for all corrupting/leakage terms. Astrophysical requirements and “rotation” can vary this number. RAS 2012: Polarimetry II

Off-axis polarimetry • Polarimetric response (and Jones matrices) generally a function of position within the primary beam. A good body of theory exists for dealing with position-variant polarimetric response. • Fractional off-axis polarization (e. g. a the half power points or beyond) can be large if uncorrected. Treat with caution! RAS 2012: Polarimetry II
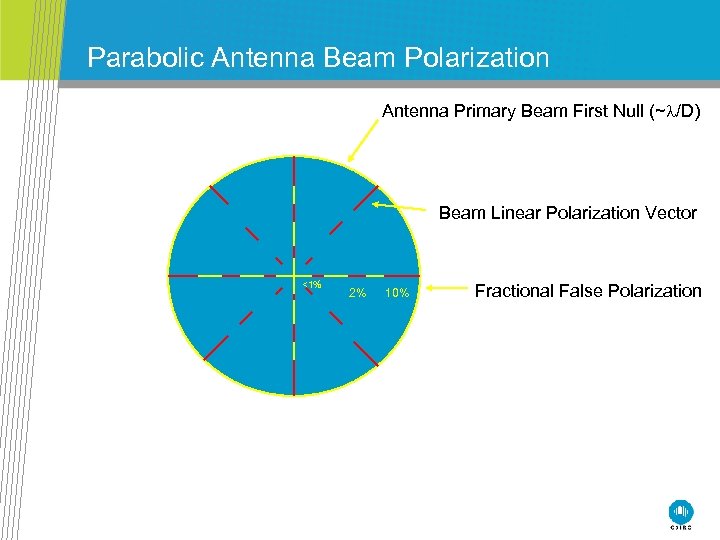
Parabolic Antenna Beam Polarization Antenna Primary Beam First Null (~l/D) Beam Linear Polarization Vector <1% 2% 10% Fractional False Polarization • Correction of polarization images for this effect is easy for equatorial mount antennas (beam is fixed on the sky), and VLA snapshot images. • Correction in the general full-synthesis case is more difficult, and is a subject of current imaging research.
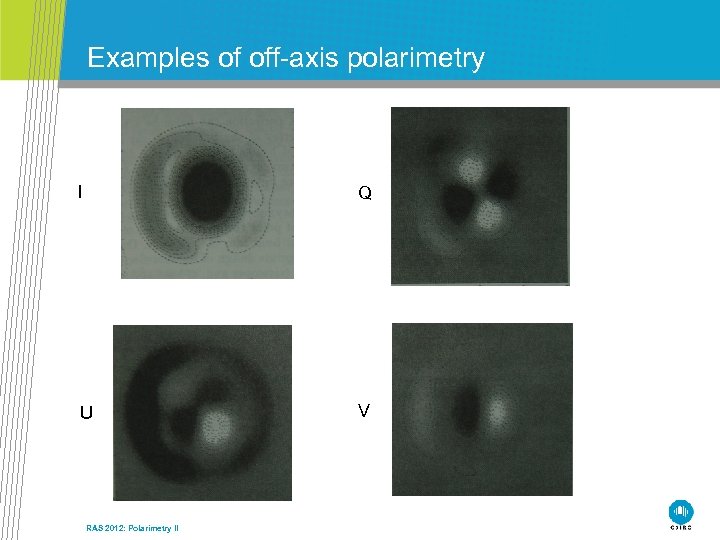
Examples of off-axis polarimetry I Q U V RAS 2012: Polarimetry II

Thank you RAS 2012: Polarimetry II
7c85a329dbd40d1167a4e14857e89fec.ppt