Показательными уравнениями неравенствами называются уравнения неравенства

• Показательными уравнениями (неравенствами) называются уравнения (неравенства), содержащие переменную в показателе степени!

Цель работы: • ввести определение показательной функции; • сформулировать её основные свойства; • показать построение графиков функции

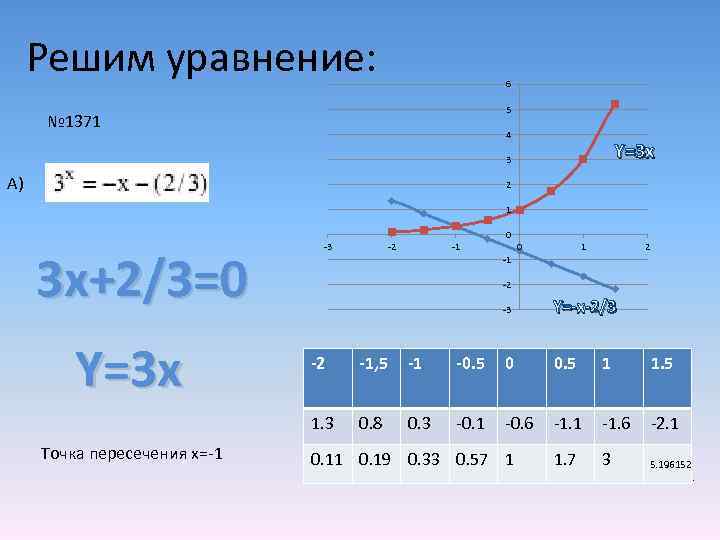Решим уравнение: 6 5 № 1371 4 Y=3 x 3 А) 2 1 0 3 x+2/3=0 Y=3 x -3 -2 -1 0 1 2 -1 -2 -3 Y=-x-2/3 -1, 5 -1 -0. 5 0 0. 5 1 1. 5 1. 3 Точка пересечения x=-1 -2 0. 8 0. 3 -0. 1 -0. 6 -1. 1 -1. 6 -2. 1 1. 7 3 5. 196152 0. 11 0. 19 0. 33 0. 57 1 .

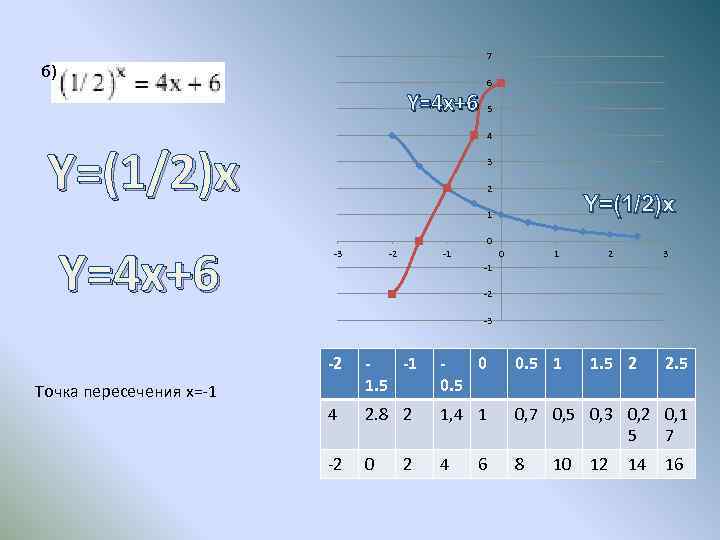7 б) 6 Y=4 x+6 5 4 Y=(1/2)x 3 2 Y=(1/2)x 1 Y=4 x+6 0 -3 -2 -1 0 1 2 3 -1 -2 -3 -2 -1 1. 5 0 0. 5 1 4 2. 8 2 1, 4 1 0, 7 0, 5 0, 3 0, 2 0, 1 5 7 -2 0 4 8 Точка пересечения x=-1 2 6 10 1. 5 2 12 14 2. 5 16

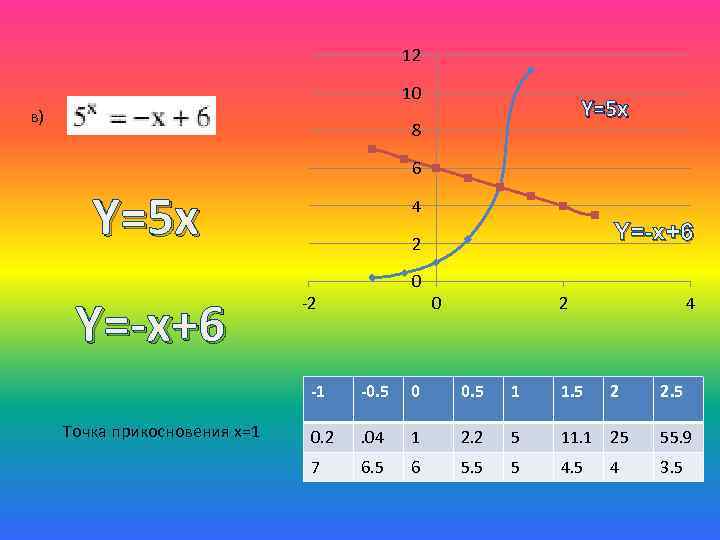12 10 в) Y=5 x 8 6 Y=5 x Y=-x+6 4 Y=-x+6 2 0 -2 0 2 4 -1 Точка прикосновения x=1 -0. 5 0 0. 5 1 1. 5 2 2. 5 0. 2 . 04 1 2. 2 5 11. 1 25 55. 9 7 6. 5 6 5. 5 5 4 3. 5

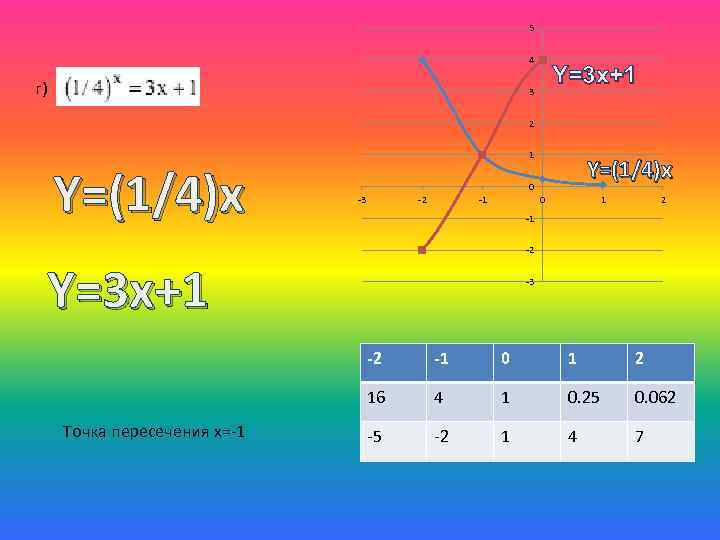5 4 г) Y=3 x+1 3 2 Y=(1/4)x 1 Y=(1/4)x 0 -3 -2 -1 0 1 2 -1 -2 Y=3 x+1 -3 -2 0 1 2 16 Точка пересечения x=-1 -1 4 1 0. 25 0. 062 -5 -2 1 4 7

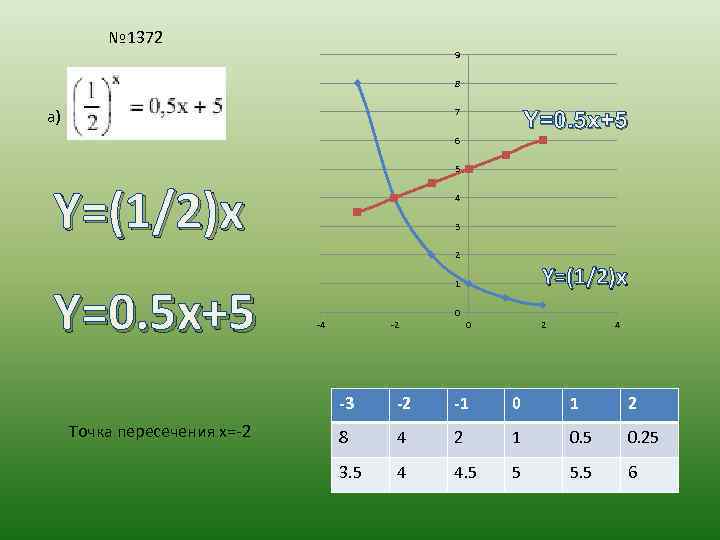№ 1372 9 8 а) 7 Y=0. 5 x+5 6 5 Y=(1/2)x 4 3 2 Y=0. 5 x+5 Y=(1/2)x 1 0 -4 -2 0 2 4 -3 Точка пересечения x=-2 -2 -1 0 1 2 8 4 2 1 0. 5 0. 25 3. 5 4 4. 5 5 5. 5 6

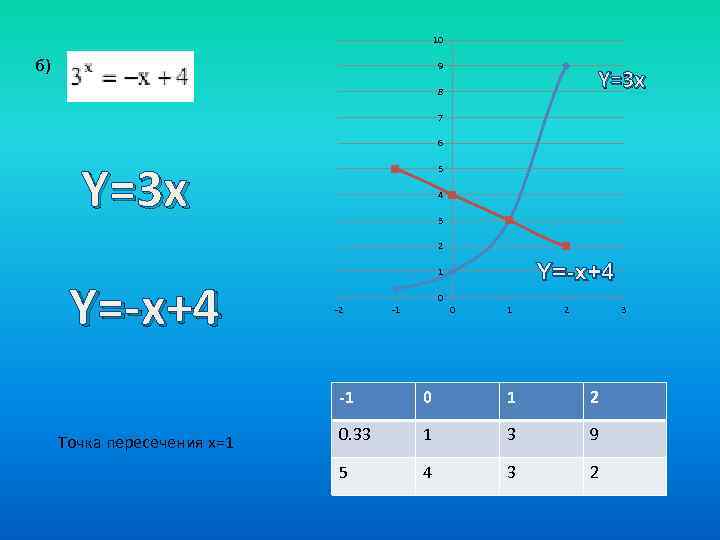10 б) 9 Y=3 x 8 7 6 Y=3 x 5 4 3 2 Y=-x+4 1 0 -2 -1 0 1 2 3 -1 Точка пересечения x=1 0 1 2 0. 33 1 3 9 5 4 3 2

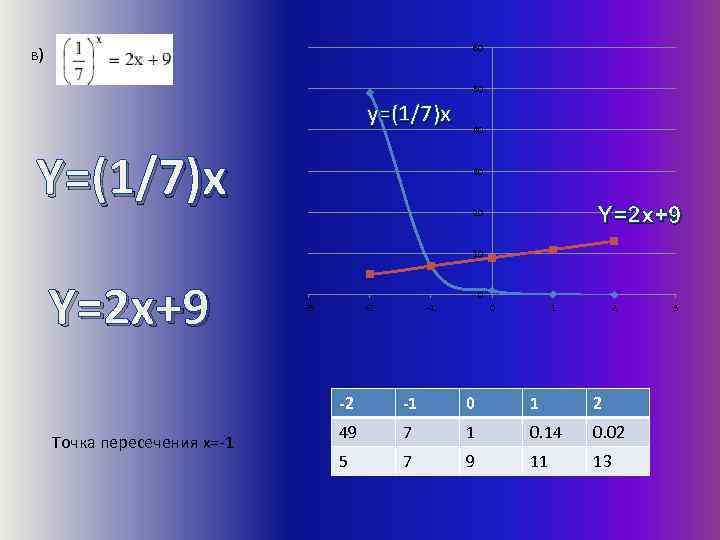60 в) 50 y=(1/7)x Y=(1/7)x 40 30 Y=2 x+9 20 10 Y=2 x+9 0 -3 -2 -1 0 1 2 -2 Точка пересечения x=-1 -1 0 1 2 49 7 1 0. 14 0. 02 5 7 9 11 13 3

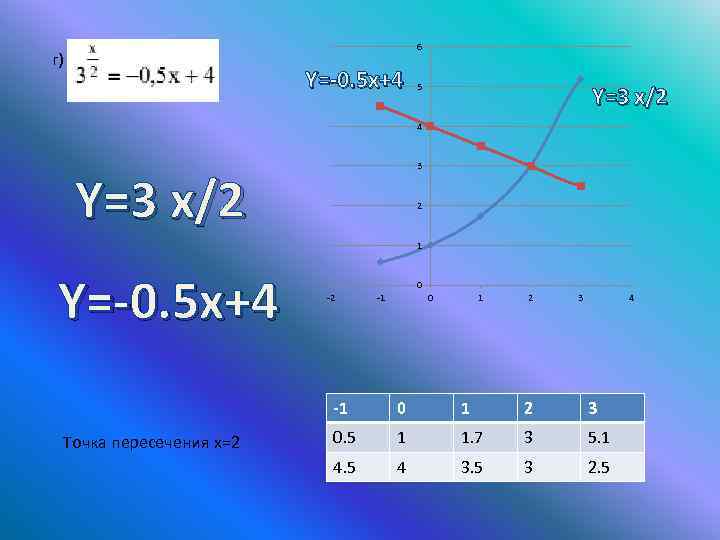6 г) Y=-0. 5 x+4 5 Y=3 x/2 4 3 Y=3 x/2 2 1 Y=-0. 5 x+4 0 -2 -1 0 1 2 3 4 -1 Точка пересечения x=2 0 1 2 3 0. 5 1 1. 7 3 5. 1 4. 5 4 3. 5 3 2. 5

The End