Показательные неравенства и способы их

Показательные неравенства и способы их решения стр. 285,

Повторение пройденного Неравенства строгие нестрогие > < ≤ ≥ Ответ: х€

Определение Показательными неравенствами называют неравенства вида: , где а>0, а≠ 1, и неравенства сводящиеся к этому виду. Пример. Решить графически неравенство: 2 х > 1 х у Решение. 0 у 8 1 7 -1 6 2 5 -2 4 3 -3 2 1 х -4 -3 -2 -1 0 1 2 3 4 5

Показательные неравенства решаются по следующим свойствам показательной функции: • если а > 1 , то неравенство a х1< а х2 справедливо х 1< х 2 • если 0 < а < 1, то неравенство a х 1 > а х 2 справедливо х 1< х 2

Решите неравенства: х 2 >0 х 1 2 x >1 х 0

Решите неравенства: 5 x >25 0, 2 x+1 < 0, 2 4 0, 7 x < 0, 49 9, 7 x-2 < 9, 7 10

Эталон ответа: n 2 х > 0 n 5 x >25 x- любое x>2 n 2 x >1 n 0, 7 x < 0, 49 x>0 x>2 х n 1 n 0, 2 x+1 < 0, 2 4 х 0 x>3 х n <0 n 9, 7 x-2 < 9, 7 10 x=Ø x < 12

Сравните • х0, 9 -5 1=1, 20 • x>y -4<0 1, 2 -4<1, 20 • x>-y 5/6 -2<6/5 -3

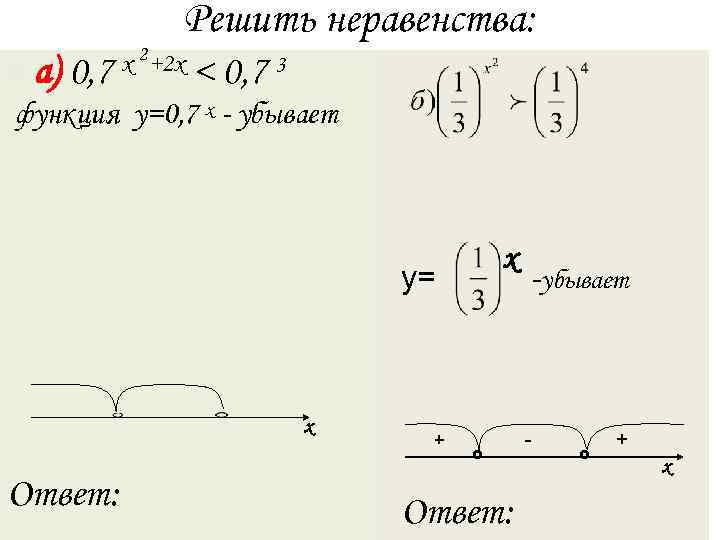
Решить неравенства: n а) 0, 7 х 2+2 х < 0, 7 3 функция y=0, 7 х - убывает х y= -убывает х -3 1 + - + ◦ х Ответ: Ответ:

Решить неравенства: n 0, 7 х 2+2 х < 0, 7 3 х2 > y=0, 7 х- убывает x 2+ 2 x > 3 х2 4 > x 2+2 x-3> 0, x 2+2 x-3=0 х x 1= -3, x 2=1 y= - убывает (x+3) (x-1)=0 x 2< 4 + _ + (х – 2)(х + 2) < 0 х -3 1 + - + ◦ -2 ◦ 2 х Ответ: (-∞; -3) (1; +∞) Ответ: (-2 ; 2)

Самостоятельная работа. • Вариант-1 • Вариант-2

Самостоятельная работа. • Вариант-1 1)

Домашнее задание. n § 47, стр 285. n Решить неравенства: а) 2³ ≤ 16 б) 9 > 27