Показатели вариации Частость относительный показатель частоты

Показатели вариации Частость – относительный показатель частоты – может быть выражен в долях единицы или процентах и позволяет сопоставлять вариационные ряды с различным числом наблюдений. Формально имеем: Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся среднее линейное отклонение, размах вариации, дисперсия, среднее квадратическое отклонение. Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: R = Xmax – Xmin. Такие показатели вариации, как среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, основаны на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической.

Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической: – абсолютное значение (модуль) отклонения варианта от средней арифметической; f– частота. Первая формула применяется, если каждый из вариантов встречается в совокупности только один раз, а вторая – в рядах с неравными частотами. Существует и другой способ усреднения отклонений вариантов от средней арифметической. Этот очень распространенный в статистике способ сводится к расчету квадратов отклонений вариантов от средней величины с их последующим усреднением.

Дисперсия (σ2) – средняя из квадратов отклонений вариантов значений признака от их средней величины (в простейшем случае несгруппированных данных): Вторая формула применяется при наличии у вариантов своих весов, дисперсия для сгруппированных данных и для интервальных рядов (или частот вариационного ряда). В экономико-статистическом анализе вариацию признака принято оценивать чаще всего с помощью среднего квадратического отклонения. Среднее квадратическое отклонение (σ) представляет собой корень квадратный из дисперсии:

Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели колеблемости: – наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.

Правило сложения дисперсий, межгрупповая дисперсия Межгрупповая дисперсия δ 2 характеризует систематическую вариацию под воздействием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних от общей средней для всей совокупности: где f — численность единиц в группе (частота). Внутригрупповая дисперсия есть уже известная нам дисперсия (для всей совокупности, называемая общей), но теперь эта формула применяется только к отдельной группе. Соответственно и обозначается она σ2 , но уже с индексом i, который подчеркивает, что расчет выполняется для отдельной i-группы. Внутригрупповая дисперсия отражает случайную вариацию, т. е. ту ее часть, которая обусловлена влиянием прочих (неучтенных) факторов, отличных от основания группировки.

По отдельным внутригрупповым дисперсиям, рассматривая их как значения некоторого особого признака, рассчитывают среднюю по внутригрупповым дисперсиям, которая уже характеризует вариацию по всей совокупности в целом под воздействием всех прочих (неучтенных) факторов, отличных от основания группировки. Существует простая и важная формула, связывающая общую дисперсию, межгрупповую дисперсию и среднюю по внутригрупповым дисперсиям: Это означает, что общая дисперсия равна сумме межгрупповой дисперсии и средней по внутригрупповым дисперсиям. Следовательно, зная две из трех дисперсий, можно всегда найти и третью.

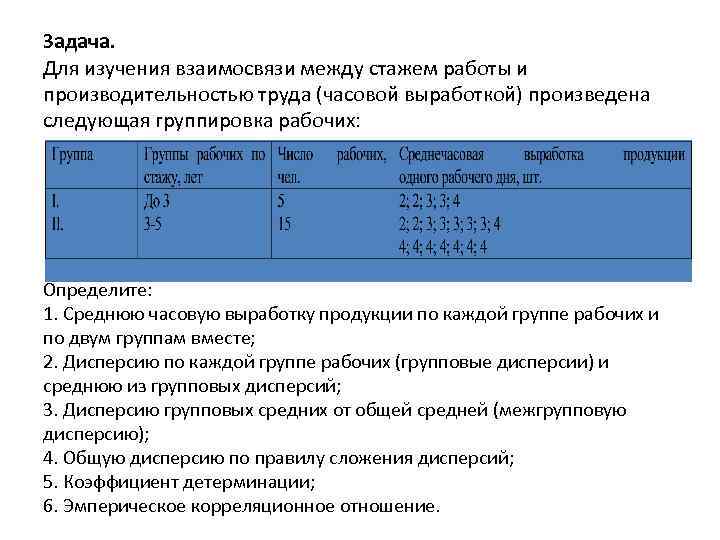Задача. Для изучения взаимосвязи между стажем работы и производительностью труда (часовой выработкой) произведена следующая группировка рабочих: Определите: 1. Среднюю часовую выработку продукции по каждой группе рабочих и по двум группам вместе; 2. Дисперсию по каждой группе рабочих (групповые дисперсии) и среднюю из групповых дисперсий; 3. Дисперсию групповых средних от общей средней (межгрупповую дисперсию); 4. Общую дисперсию по правилу сложения дисперсий; 5. Коэффициент детерминации; 6. Эмперическое корреляционное отношение.

Вторая группа Решение. Определим среднюю выработку по каждой группе рабочих и по двум группам. Исчислим дисперсии по каждой группе рабочих по формуле: Предварительно строим по каждой группе рабочих ряды распределения по выработке. Затем исчислим групповые дисперсии. Первая группа Вторая группа

Дисперсия для первой группы: Дисперсия для второй группы: Исчислим среднюю из групповых (частных) дисперсий по формуле: 3. Межгрупповая дисперсия: 4. Определим общую дисперсию по правилу сложения дисперсий: 5. Определяем коэффициент детерминации: Коэффициент детерминации показывает, что вариация среднечасовой выработки рабочих обусловлена вариацией стажа лишь на 11, 5%. 6. Исчислим эмпирическое корреляционное отношение: Оно показывает, что для данной группы рабочих связь между производственным стажем и среднечасовой выработкой незначительная.