Поиск подстроки образца в строке string-matching Алгоритмы Рабина-Карпа

Зарегистрируйтесь, чтобы просмотреть полный документ!

Поиск подстроки (образца) в строке (string-matching) Алгоритмы: Рабина-Карпа Хорспула Кнута-Морриса-Пратта, Бойера-Мура

Алгоритм прямого перебора Пусть S строка (набор символов из некоторого алфавита, называемый текстом), где нужно произвести поиск строки P (набор символов, называемый шаблоном или образцом). n - длина строки S, а m - длина строки P (m≤n). Сравниваем сначала первые m символов строки S с соответствующими m символами строки P. Если все символы в парах окажутся равными, то на этом поиск заканчивается – образец в тексте найден. В противном случае, начало поиска сдвигается на одну позицию вправо и осуществляется сравнение следующих m символов и так до тех пор пока, либо все символы не совпадут, либо после n-m сдвигов не будет достигнут конец строки S.

Алгоритм прямого перебора Результатом является указатель на первый символ в строке S, с которого начинается искомая строка в случае удачи, либо NULL, если строка P не найдена. Этот алгоритм достаточно эффективен в том случае, когда несовпадение пар символов происходит после всего лишь нескольких сравнений. Поскольку наибольшее количество таких проверок равно n-m+1 (далее проверять не надо, т. к. размер оставшейся части строки меньше размера шаблона) и в наихудшем случае при каждой проверке требуется выполнить m сравнений, общее количество сравнений в наихудшем случае равно (n-m+1)*m, так что производительность алгоритма (метод грубой силы) в наихудшем случае равна Θ((n-m+1)*m).

Алгоритм прямого перебора В среднем, однако, можно ожидать, что при каждой проверке будет сделано только несколько сравнений; в самом деле, для случайного естественного текста эффективность в среднем случае превращается в Θ(n). Графически этот алгоритм можно интерпретировать как скольжение шаблона с образцом по тексту, в процессе которого отмечается, для каких сдвигов все символы шаблона равны соответствующим символам текста. Чем меньше совпавших символов, тем быстрее шаблон смещается по строке в которой ведется поиск.

Алгоритм прямого перебора Naive_String_Matcher (S, P) n = length S // длина текста m = length P // длина шаблона for i = 0 to n - m do if (P[1. . m] == S[i+1. . i+m]) then print “Вхождение при сдвиге s”

Алгоритм Рабина-Карпа (1981 г. ) Возьмем некоторую функцию, определенную на словах длины m. Если значения этой функции на слове длины m в шаблоне S и подстроке в строке P различны, то совпадения нет. Только если значения одинаковы, нужно проверять совпадение по буквам. При сдвиге шаблона сравниваемое с шаблоном слово не меняется полностью, а лишь одна буква добавляется в конце и одна буква убирается в начале. По этим данным нужно так выбрать функцию, чтобы можно было просто рассчитать, как меняется функция при сдвиге шаблона.

Алгоритм Рабина-Карпа (1981 г. ) Пример. Заменим все символы в слове и образце их номерами (ASCII-кодами), представляющими собой целые числа. Тогда удобной функцией является сумма кодов символов. Если получающееся число будет очень большим, то его можно брать по модулю некоторого числа q. При сдвиге шаблона нужно добавить код добавляемого символа и вычесть код удаленного символа. Для каждой функции существуют слова, к которым она применима плохо. Зато другая функция в этом случае может работать хорошо. Идея: надо запасти много функций и в начале работы алгоритма выбирать из них случайную.

Алгоритм Рабина-Карпа (1981 г. ) Пример. Выберем некоторое число p (желательно простое). Каждое слово длины m будем рассматривать как коэффициенты многочлена степени m-1 и вычислим значение этого многочлена по модулю p в точке x. Сдвиг на 1 соответствует вычитанию старшего члена, умножению на x и добавлению свободного члена. Оценим время работы алгоритма. Значение функции на шаблоне вычисляется за время Θ(m), а n-m+1 значений функций – за время Θ(n-m+1). Фаза сравнения значений функций требует Θ(nm+1) времени.

Алгоритм Рабина-Карпа (1981 г. ) Таким образом, на предварительную обработку затрачивается время Θ(m), а время сравнения в наихудшем случае равно Θ((n-m+1)*m), т. е. не лучше, чем во время работы простейшего алгоритма. Однако, на практике в среднем он работает намного лучше. Можно все символы алфавита интерпретировать, как цифры в системе счисления по основанию d, где d – количество символов в алфавите. Тогда слово очень просто записывается, как число в этой системе счисления, просто, как совокупность тех же символов.

Алгоритм Рабина-Карпа (1981 г. ) Rabin_Karp_Matcher(S, P, d, q) n=length[S]; m=length[P]; h=dm-1 modq; p=0; s 0=0; for i=1 to m ►Предварительная проверка do p=(dp+P[i]) mod q; s 0=(ds 0+S[i]) mod q for j=0 to n-m ►Проверка do if p=sj then if P[1. . m]=S[j+1. . j+m] then print ”Образец обнаружен при сдвиге j” if j<n-m then sj+1=(d(sj-S[s+1]h)+S[j+m+1])mod q

Алгоритм Хорспула (1980 г. ) Мы начнем с рассмотрения упрощенной версии алгоритма Бойера-Мура, предложенной Хорспулом в 1980 году. Как и в алгоритме Бойера-Мура в алгоритме Хорспула выравнивание образца начинается по первому символу текста, а проверка же выполняется путем сравнения символов образца и текста справа налево, начиная с последнего символа образца. Пусть С последний символ текста, который при выравнивании находится напротив последнего символа образца. В общем случае могут возникнуть четыре разные ситуации.

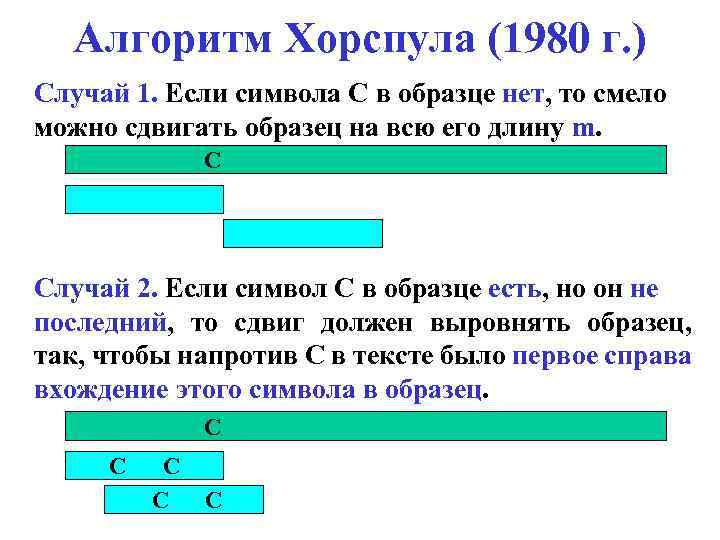
Алгоритм Хорспула (1980 г. ) Случай 1. Если символа С в образце нет, то смело можно сдвигать образец на всю его длину m. C Случай 2. Если символ С в образце есть, но он не последний, то сдвиг должен выровнять образец, так, чтобы напротив С в тексте было первое справа вхождение этого символа в образец. C C C

Алгоритм Хорспула (1980 г. ) Случай 3. Если С – последний символ образца и среди остальных m-1 символов образца такого символа нет, то образец следует сдвинуть на всю длину m. C C C Случай 4. Если С – последний символ образца и среди остальных m-1 символов образца имеются другие вхождения этого символа, то сдвиг должен быть подобен случаю 2. C С C

Алгоритм Хорспула (1980 г. ) Мы можем предварительно вычислить величины сдвигов для каждого возможного символа и хранить их в таблице. Такая таблица индексируется всеми символами, которые могут встретиться в тексте, включая, для естественных языков, пробелы, символы пунктуации и другие специальные символы. Элементы таблицы заполняются величинами сдвигов. В частности, для каждого символа С мы можем вычислить величину сдвига по формуле: m, если С нет среди первых m-1 символов образца t(C) = расстояние до крайнего справа символа С среди первых m-1 символов образца от его последнего символа

Алгоритм Хорспула (1980 г. ) Вот простой алгоритм для вычисления элементов таблицы сдвигов. Все значения инициализируются длиной образца m, а затем выполняется сканирование образца слева направо с выполнением m-1 раз следующих действий: для j-го символа образца (0≤j≤m-2) соответствующий ему элемент таблицы перезаписывается значением m-1 j, которое представляет собой расстояние от символа до правого конца образца. Заметим, что, поскольку алгоритм сканирует образец слева направо, последняя перезапись выполняется, когда встречается самое правое вхождение символа в образец, т. е. именно так, как требуется.

Алгоритм Хорспула (1980 г. ) Shift. Table(P[0. . m-1]) Инициализация всех элементов таблицы значениями m for j=0 to m-2 do Table[P[j]] = m-1 -j return Table

Алгоритм Хорспула (1980 г. ) Алгоритм Хорспула. Шаг 1. Для данного образца длиной m и алфавита, используемого в тексте и образце, описанным выше способом строится таблица сдвигов. Шаг 2. Выравниваем начало образца с началом текста. Шаг 3. Начиная с последнего символа образца, сравниваем соответствующие символы в образце и тексте, пока не будет установлено равенство всех m символов, либо пока не будет обнаружена пара разных символов. В последнем случае находим элемент t(C) из таблицы сдвигов и сдвигаем образец вдоль текста на t(C) символов вправо.

Алгоритм Бойера-Мура (1975 г. ) Если первое сравнение крайнего справа символа в образце с соответствующим символом С в тексте показывает, что они различны, алгоритм работает точно так же, как и алгоритм Хорспула, т. е. выполняется сдвиг вправо на количество символов, которое определяется таблицей сдвигов. Однако алгоритмы Бойера-Мура и Хорспула работают по-разному, если некоторое положительное количество k символов образца совпадает с символами текста, перед тем как встретится первое отличие. В этой ситуации алгоритм Бойера-Мура определяется величину сдвигов, рассматривая две величины.

Алгоритм Бойера-Мура (1975 г. ) Величина первого сдвига определяется символом текста С, который первым не соответствует символу образца при сравнении справа налево. Назовем его сдвигом несовпадающего символа. Рассмотрение данного сдвига выполняется так же, как и сдвига в алгоритме Хорспула. Если символ С не входит в образец, мы сдвигаем образец так, чтобы символ С вышел за пределы образца. Значение этого сдвига легко вычислить по формуле t 1(C)-k. Та же формула используется и в случае, когда несовпадающий символ С имеется в образце и при этом t 1(C)-k>0.

Алгоритм Бойера-Мура (1975 г. ) Если t 1(C)-k≤ 0, то очевидно, нельзя сдвигать образец на нулевое или отрицательное количество позиций. Вместо этого мы просто применяем метод грубой силы и сдвигаем образец на одну позицию вправо. Сдвиг можно выразить простой компактной формулой: d=max{t 1(C)-k, 1}. Сдвиг второго типа определяется совпадением последних k>0 символом образца. Будем называть конечную часть образца его суффиксом длиной k и обозначать как suff(k). Соответственно, этот тип сдвига будем называть сдвигом совпадающего суффикса (good-suffix shift).

Алгоритм Бойера-Мура (1975 г. ) Если имеется другая последовательность suff(k), которую предваряет символ, отличный от символа, предваряющего последнюю такую последовательность символов. В таком случае мы можем сдвинуть образец на расстояние d 2 между второй справа последовательностью suff(k) и такой же последовательностью, крайней справа в образце. Если в образце нет другой последовательности suff(k), которой предшествует символ, отличный от символа, предшествующего суффиксу suff(k), то следует найти наибольший префикс длиной l<k, совпадающий с суффиксом той же длины l.

Алгоритм Бойера-Мура (1975 г. ) Если такой префикс имеется, величина сдвига d 2 вычисляется как расстояние между префиксом и суффиксом; в противном случае d 2 устанавливается равным длине образца m.

Алгоритм Бойера-Мура (1975 г. ) Алгоритм Бойера-Мура. Шаг 1. Для данного образца и используемого алфавита строится таблица сдвигов несовпадающих символов. Шаг 2. Для данного образца строится таблица символов совпадающих суффиксов. Шаг 3. Начиная с последнего символа образца, сравниваем соответствующие символы в образце и тексте, пока не будет установлено равенство всех m символов, либо пока не будет обнаружена пара разных символов после k≥ 0 совпадающих символов. Сдвигаем образец вправо на количество позиций: d=d 1, если k=0 и d=max{d 1, d 2}, если k>0.

Алгоритм Бойера-Мура (1975 г. ) Пример. Рассмотрим поиск подстроки BAOBAB в тексте, состоящем из английских букв и пробелов. Таблица сдвигов несовпадающих символов: c A B C D … O … Z _ t 1 1 2 6 6 6 3 6 6 6 Таблица сдвигов совпадающих суффиксов: k Образец d 2 1 BAOBAB 2 2 BAOBAB 5 3 BAOBAB 5 4 BAOBAB 5 5 BAOBAB 5

Алгоритм Бойера-Мура (1975 г. ) BESS_KNEW_ABOUT_BAOBABS BAOBAB d 1=t 1(K)-0=6 BAOBAB d 1=t 1(_)-2=4 d 2=5 d=max{4, 5}=5 BAOBAB d 1=t 1(_)-1=5 d 2=2 d=max{4, 5}=5

Пример. //Поиск в строке по алгоритму Бойера-Мура #include <stdio. h> #include <string. h> #include <conio. h> int BM(char *S, char *P); void main() { char S[]="Иванович Иваникин"; char P[]="Иваникин"; int r; clrscr(); r = BM(S, P);

Пример. if(r<0) printf("n Подстрока "%s" не найдена", P); else printf("n Подстрока "%s" найдена, позиция i=%d", P, r); getch(); } //Поиск подстроки по алгоритму Бойера-Мура int BM(char *S, char *P) // S-исходная строка, P-строка-образец { int i, j, k, M, N, t; int d[256]; i=0; M=strlen(P); N=strlen(S); for(j=0; j<256; j++) d[j]=M; for(j=0; j<256; j++) d[(unsigned char)P[j]]=M-j-1;

Пример. //Поиск подстроки в строке j=M; while((j>0)&&(i<=N)) { j=M; k=i; while((j>0)&&(S[k-1]==P[j-1])) {k--; j--; } t=d[(unsigned char)S[i-1]]; i=i+t; } if(j<=0) return i-M-t; //строка найдена с позиции i-M-t else return 0; //строка не найдена }

Алгоритм Кнута-Морриса-Пратта (1970 г. ) базируется на том, что после частичного совпадения начальной части строки P с соответствующими символами строки S и при несовпадении очередной пары символов сдвиг производится на пройденное расстояние, если в нем нет начального символа строки P, либо до позиции с начальным символом. Алгоритм КМП дает выигрыш только тогда, когда после очередного сдвига неудаче предшествует некоторое совпадение символов.

Алгоритм Кнута-Морриса-Пратта Полезную информацию, позволяющую сделать вывод о допустимых сдвигах, можно получить путем сравнения образца с самим собой. Вычисляется самый длинный префикс образца, который также является его собственным суффиксом. Эти данные предварительно вычисляются и заносятся в массив π. Если первые q символов совпали при сдвиге s, то следующий сдвиг, который может оказаться допустимым, равен s’ = s + (q – π[q]). Префиксная функция π, предназначенная для какого-нибудь образца, содержит сведения о том, в какой мере образец совпадает сам с собой после сдвигов.

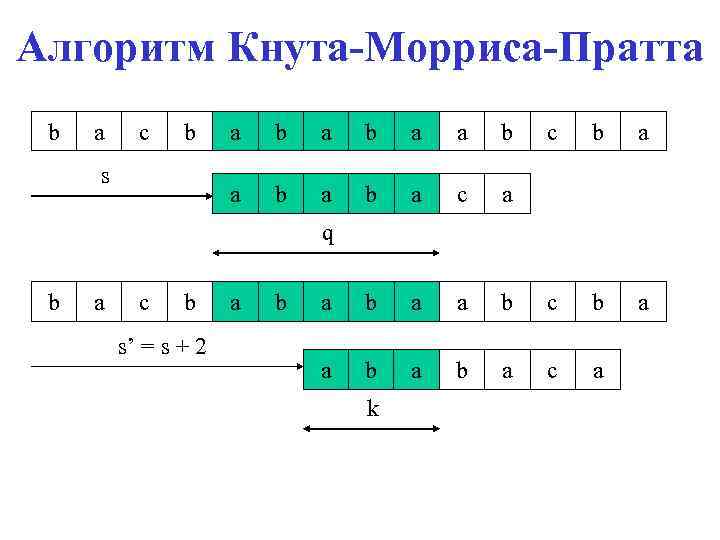
Алгоритм Кнута-Морриса-Пратта b a c b b a a b a s a c b a b a c a a b c b a a b a c a q b a c b s’ = s + 2 a b k

Алгоритм Кнута-Морриса-Пратта KMP_Matcher(T, P) n = length[T] m = length[P] π = Compute_Prefix_Function(P) q = 0 for i=1 to n do while q>0 и P[q+1]≠T[i] do q=π[q] if P[q+1]=T[i] then q=q+1 if q=m then print “Образец обнаружен при сдвиге”i-m q=π[q]

Алгоритм Кнута-Морриса-Пратта Compute_Prefix_Function(P) m = length[P] π[1]=0 k=0 for q=2 to m do while k>0 и P[k+1]≠P[q] do k=π[k] if P[k+1]=P[q] then k=k+1 π[q]=k return π

Пример. //Поиск с строке по алгоритму Кнута-Морриса-Пратта #include <stdio. h> #include <string. h> #include <conio. h> int KMP(char *S, char *P); void main() { char S[]="Иванович Иваникин"; char P[]="Иваникин"; int r; clrscr(); r = KMP(S, P);

Пример. if(r<0) printf("n Подстрока "%s" не найдена", P); else printf("n Подстрока "%s" найдена, позиция i=%d", P, r); getch(); } //Поиск подстроки по алгоритму Кнута-Морриса-Пратта int KMP(char *S, char *P) //S - исходная строка, //P - строка-образец { int i, j, k, M, N; int d[100]; M=strlen(P); N=strlen(S); d[0]=-1; j=0; k=-1;

Пример. while(j<(M-1)) { while((k>=0)&&(P[j]!=P[k])) k=d[k]; j++; k++; if(P[j]==P[k]) d[j]=d[k]; else d[j]=k; } i=0; j=0; k=0; while((j<M)&&(i<N)) { while((j>=0)&&(S[i]!=P[j]))j=d[j]; i++; j++; } if(j==M) return i-M; //Найдена позиция i-M else return 0; }

Скачать презентацию Поиск подстроки образца в строке string-matching Алгоритмы Рабина-Карпа

Лекция 20 Поиск в строках по образцу.ppt

Количество слайдов: 36