Поиск кратчайшего пути в графе Алгоритм Дейкстры

Поиск кратчайшего пути в графе Алгоритм Дейкстры

Типичные задачи, связанные с поиском путей в графе 1. Поиск пути в лабиринте; 2. Поиск минимального пути между заданными вершинами; 3. Поиск максимального пути между заданными вершинами; 4. Поиск циклов Эйлера (пройти по всем ребрам и вернуться в начальную вершину); 5. Поиск циклов Гамильтона (пройти по всем вершинам и вернуться в начальную). Для каждой задачи существует несколько вариантов решений.

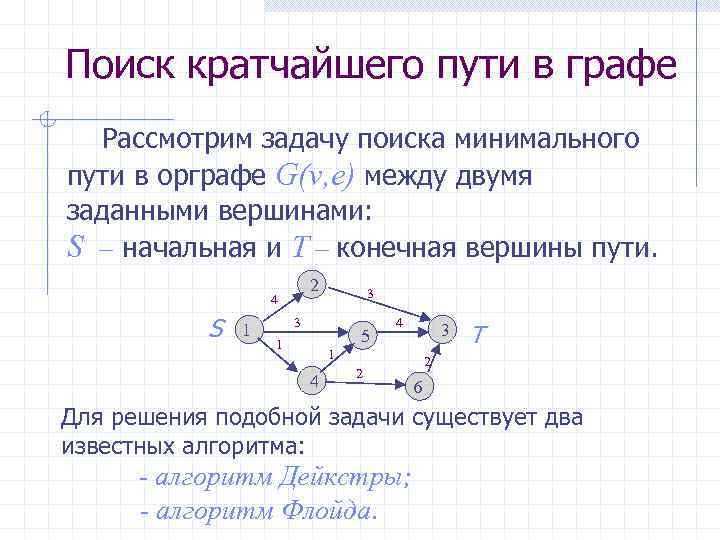Поиск кратчайшего пути в графе Рассмотрим задачу поиска минимального пути в орграфе G(v, e) между двумя заданными вершинами: S – начальная и T – конечная вершины пути. 2 4 S 1 3 3 5 1 4 3 1 4 2 Т 2 6 Для решения подобной задачи существует два известных алгоритма: - алгоритм Дейкстры; - алгоритм Флойда.

Алгоритм Дейкстры

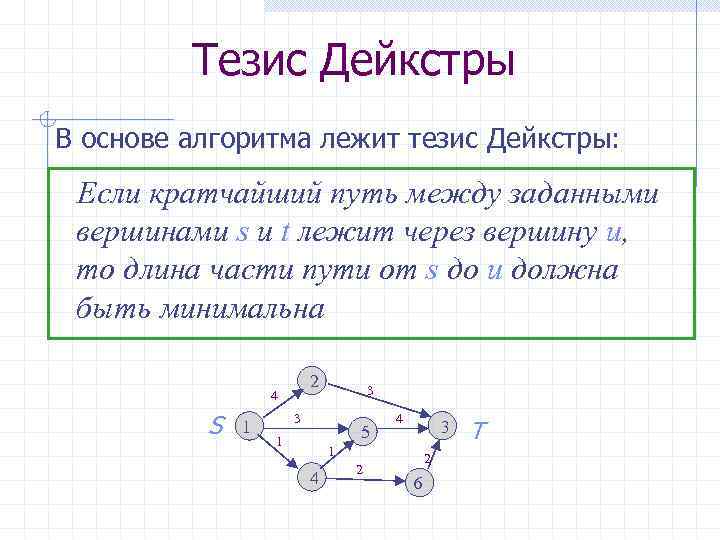Тезис Дейкстры В основе алгоритма лежит тезис Дейкстры: Если кратчайший путь между заданными вершинами s и t лежит через вершину u, то длина части пути от s до u должна быть минимальна 2 4 S 1 3 3 5 1 4 3 1 4 2 2 6 Т

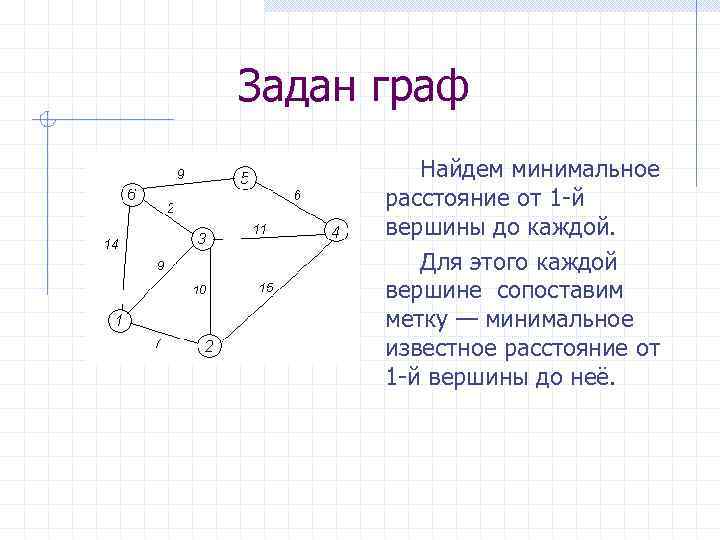Задан граф Найдем минимальное расстояние от 1 -й вершины до каждой. Для этого каждой вершине сопоставим метку — минимальное известное расстояние от 1 -й вершины до неё.

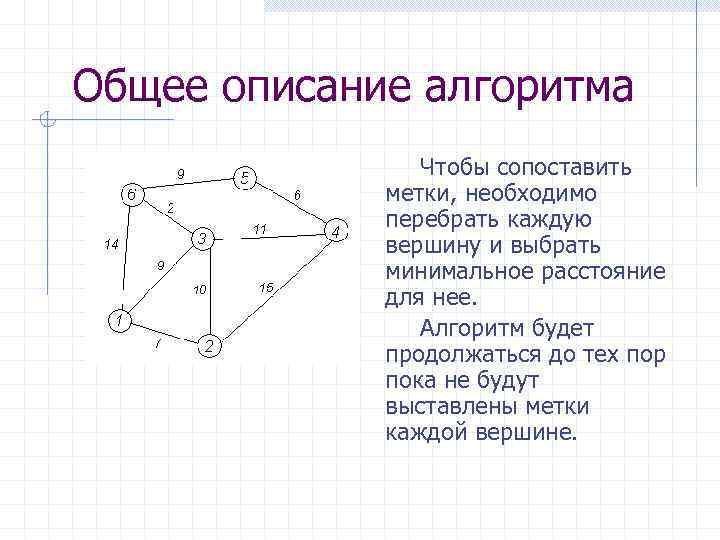Общее описание алгоритма Чтобы сопоставить метки, необходимо перебрать каждую вершину и выбрать минимальное расстояние для нее. Алгоритм будет продолжаться до тех пор пока не будут выставлены метки каждой вершине.

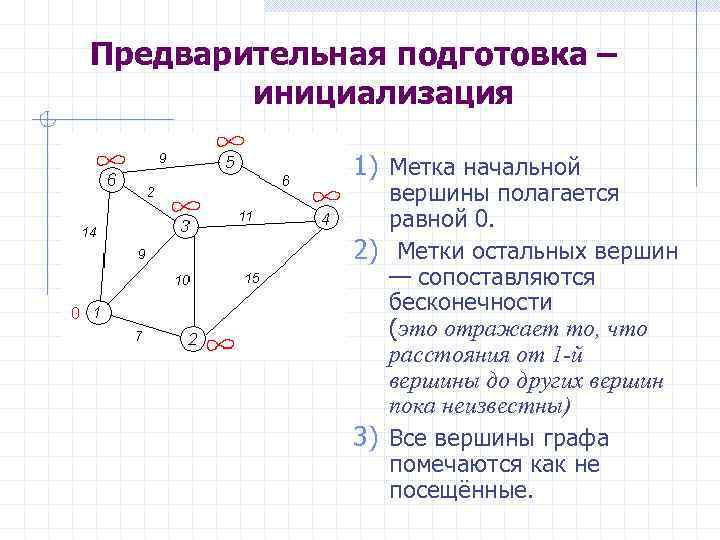Предварительная подготовка – инициализация 1) Метка начальной вершины полагается равной 0. 2) Метки остальных вершин — сопоставляются бесконечности (это отражает то, что расстояния от 1 -й вершины до других вершин пока неизвестны) 3) Все вершины графа помечаются как не посещённые.

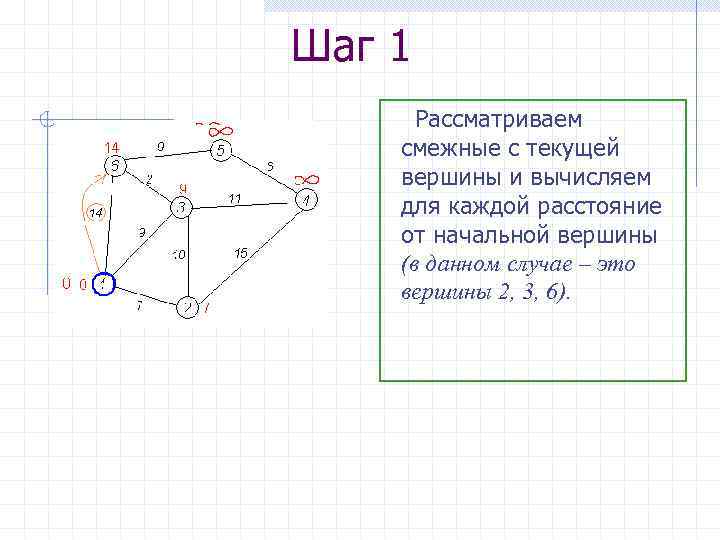Шаг 1 Рассматриваем смежные с текущей вершины и вычисляем для каждой расстояние от начальной вершины (в данном случае – это вершины 2, 3, 6).

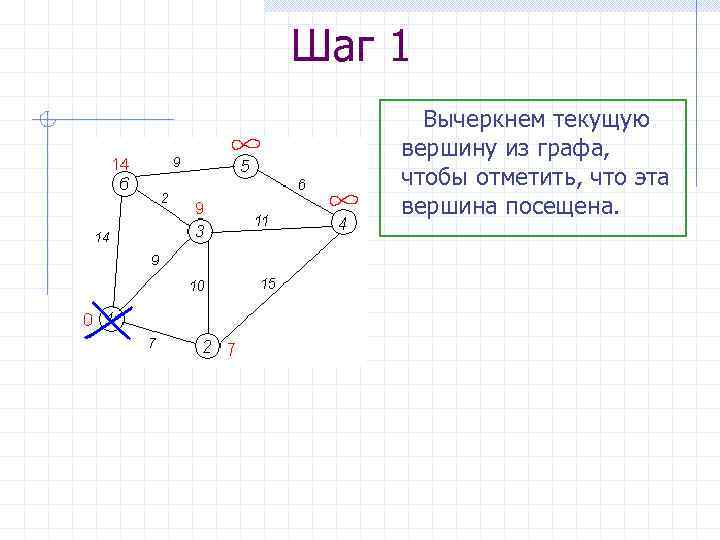Шаг 1 Вычеркнем текущую вершину из графа, чтобы отметить, что эта вершина посещена.

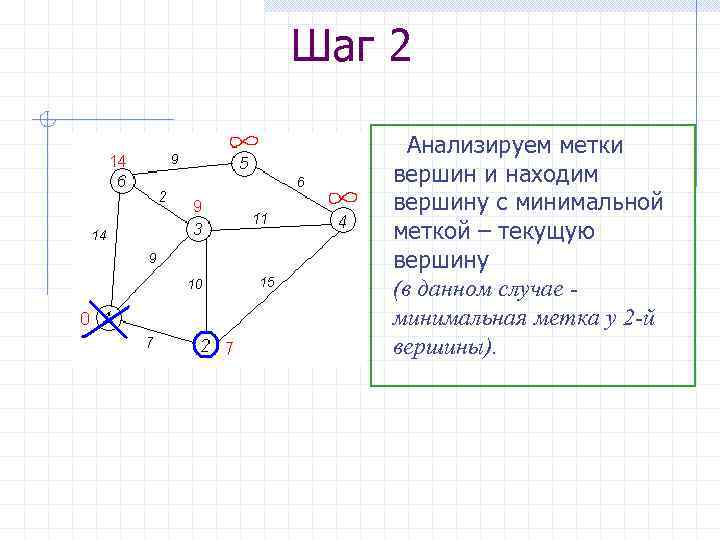Шаг 2 Анализируем метки вершин и находим вершину с минимальной меткой – текущую вершину (в данном случае - минимальная метка у 2 -й вершины).

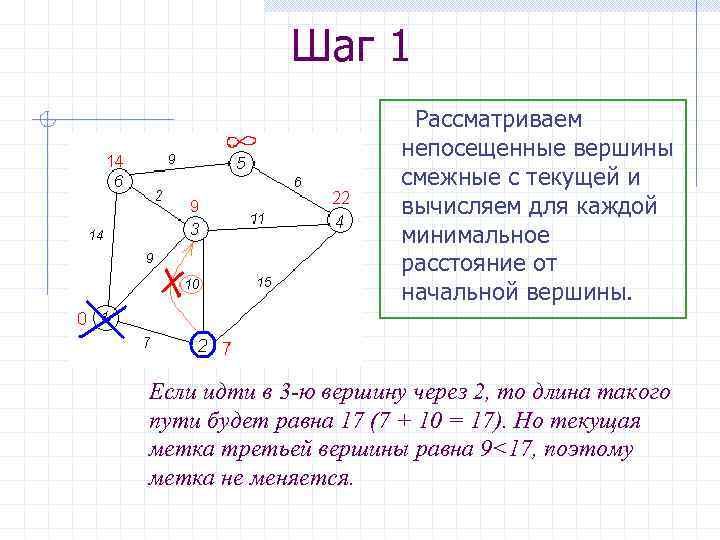Шаг 1 Рассматриваем непосещенные вершины смежные с текущей и вычисляем для каждой минимальное расстояние от начальной вершины. Если идти в 3 -ю вершину через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.

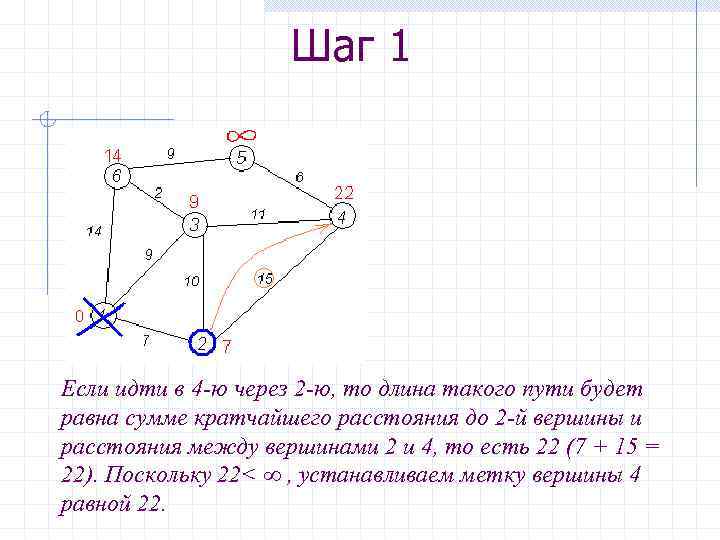Шаг 1 Если идти в 4 -ю через 2 -ю, то длина такого пути будет равна сумме кратчайшего расстояния до 2 -й вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 = 22). Поскольку 22< ∞ , устанавливаем метку вершины 4 равной 22.

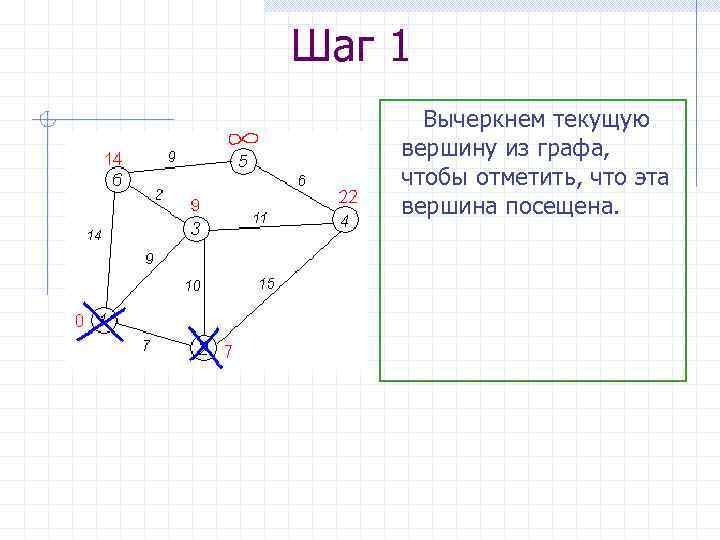Шаг 1 Вычеркнем текущую вершину из графа, чтобы отметить, что эта вершина посещена.

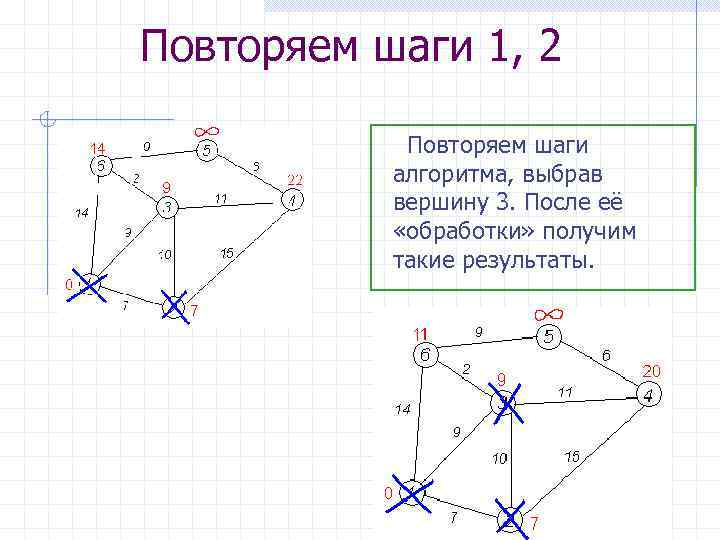Повторяем шаги 1, 2 Повторяем шаги алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты.

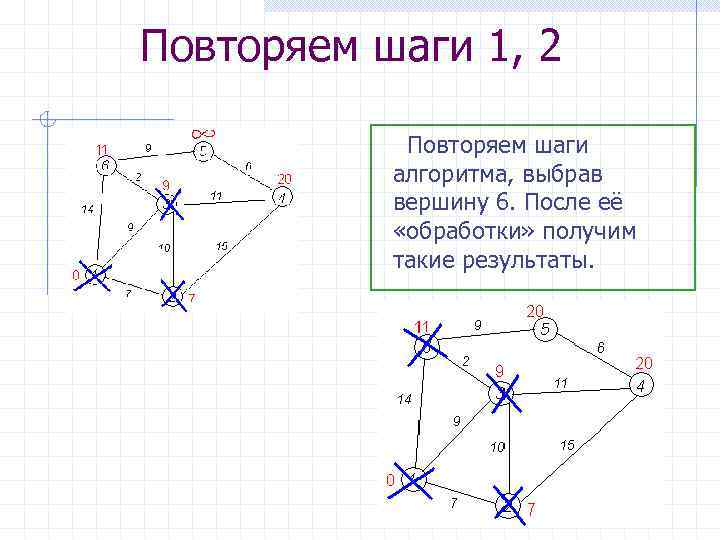Повторяем шаги 1, 2 Повторяем шаги алгоритма, выбрав вершину 6. После её «обработки» получим такие результаты.

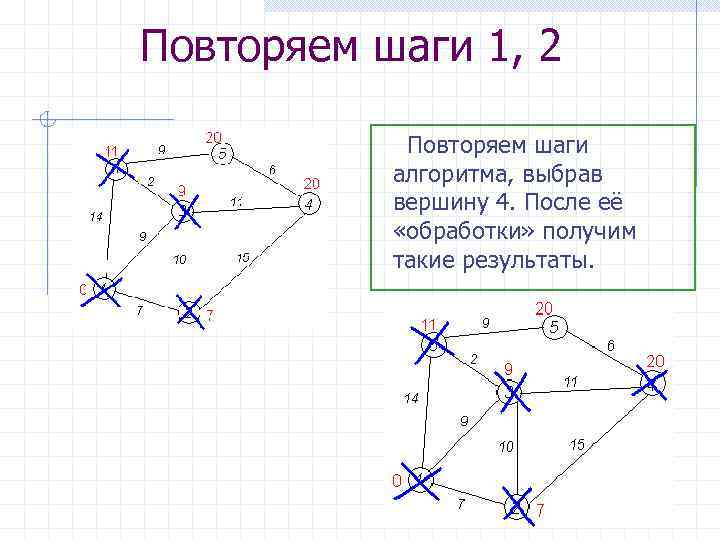Повторяем шаги 1, 2 Повторяем шаги алгоритма, выбрав вершину 4. После её «обработки» получим такие результаты.

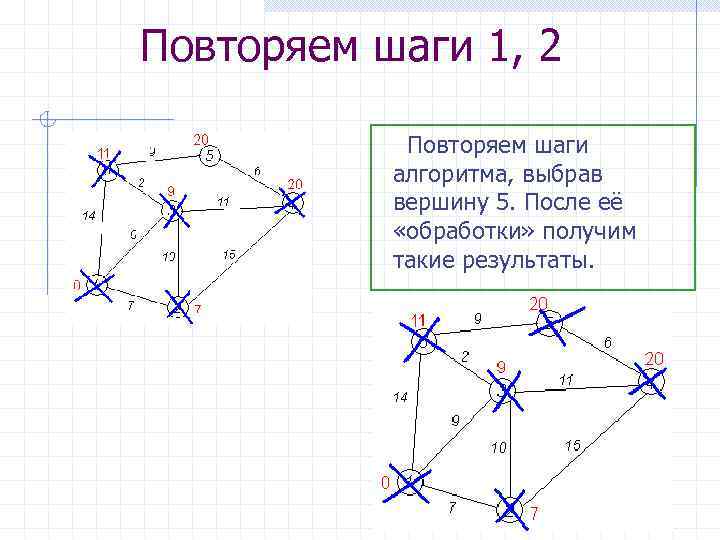Повторяем шаги 1, 2 Повторяем шаги алгоритма, выбрав вершину 5. После её «обработки» получим такие результаты.

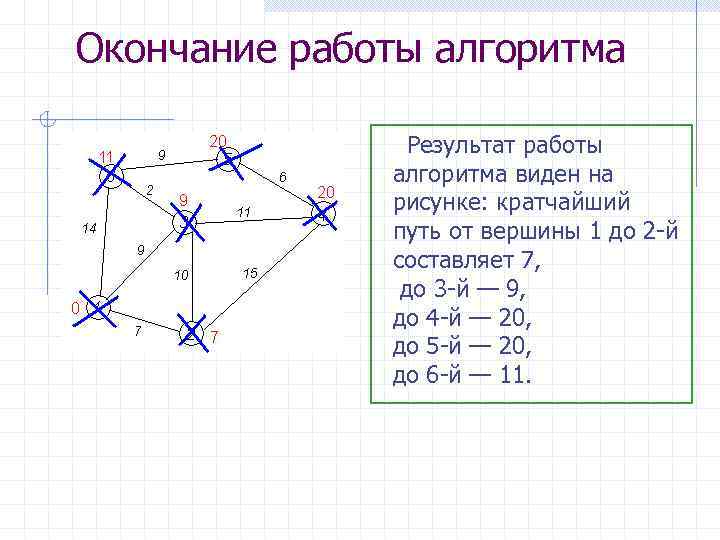Окончание работы алгоритма Результат работы алгоритма виден на рисунке: кратчайший путь от вершины 1 до 2 -й составляет 7, до 3 -й — 9, до 4 -й — 20, до 5 -й — 20, до 6 -й — 11.

Алгоритм Дейкстры Программное решение

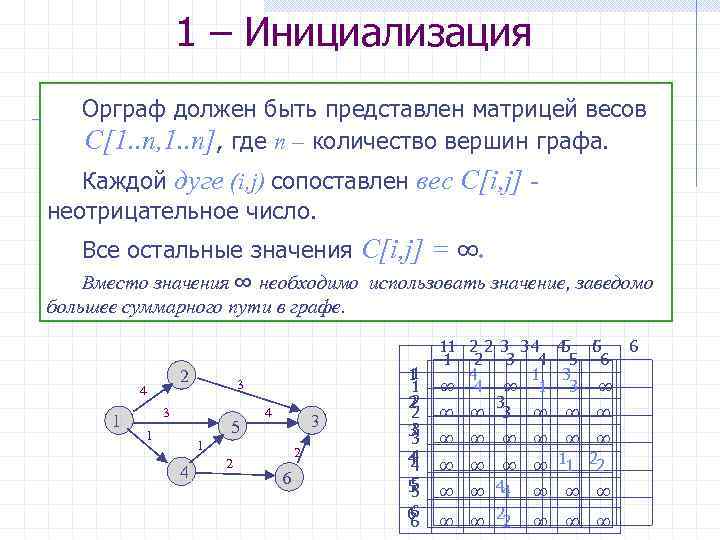1 – Инициализация Орграф должен быть представлен матрицей весов C[1. . n, 1. . n], где n – количество вершин графа. Каждой дуге (i, j) сопоставлен вес С[i, j] - неотрицательное число. Все остальные значения С[i, j] = ∞. Вместо значения ∞ необходимо использовать значение, заведомо большее суммарного пути в графе. 2 4 1 3 3 5 1 4 3 1 4 2 2 6 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 11 2 2 3 3 4 4 5 6 5 1 2 3 4 5 6 4 1 3 ∞ 4 ∞ 1 3 ∞ ∞ ∞ ∞ ∞ ∞ ∞ 11 22 ∞ ∞ 4 4 ∞ 2 2 ∞ ∞ ∞ 6

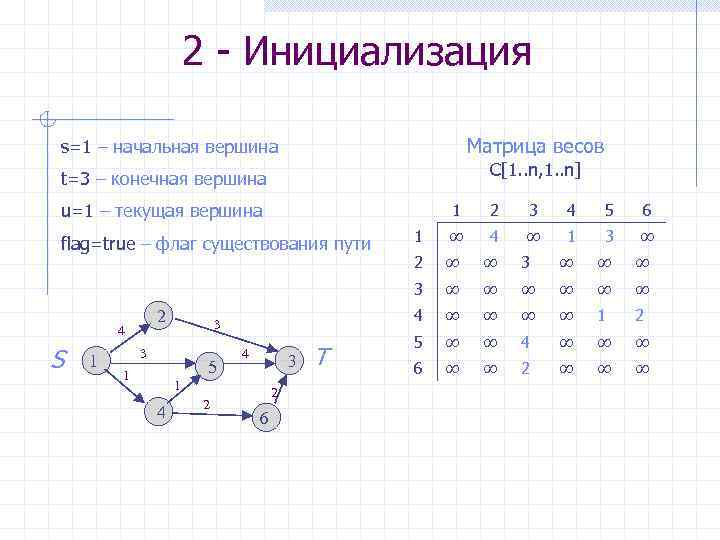2 - Инициализация Матрица весов s=1 – начальная вершина C[1. . n, 1. . n] t=3 – конечная вершина u=1 – текущая вершина 1 2 4 S 1 3 5 1 4 3 1 4 2 2 6 Т 4 5 6 1 ∞ 4 ∞ 1 3 ∞ 2 ∞ ∞ 3 ∞ ∞ ∞ ∞ ∞ 4 3 3 3 flag=true – флаг существования пути 2 ∞ ∞ 1 2 5 ∞ ∞ 4 ∞ ∞ ∞ 6 ∞ ∞ 2 ∞ ∞ ∞

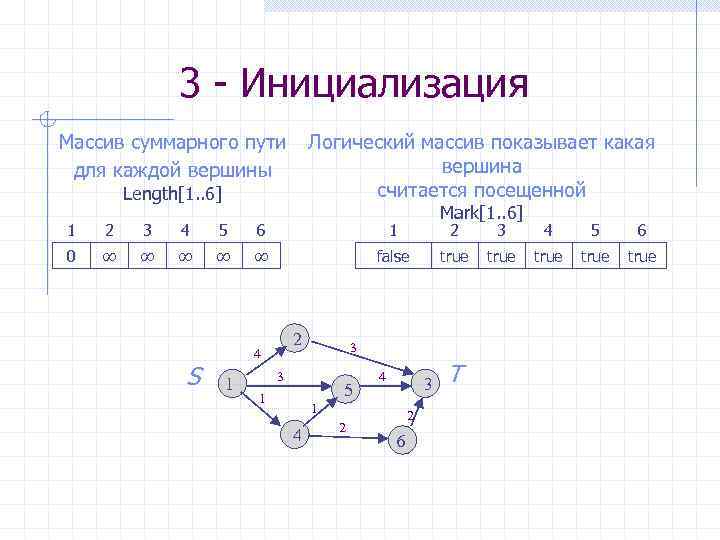3 - Инициализация Массив суммарного пути для каждой вершины Логический массив показывает какая вершина считается посещенной Length[1. . 6] Mark[1. . 6] 1 2 3 4 5 6 1 0 ∞ ∞ ∞ false S 2 4 1 5 4 4 5 6 true 3 1 4 3 true 3 3 1 2 2 2 6 Т

Пояснения к начальным присваиваниям 1) Матрица весов C[1. . n, 1. . n], где n – количество вершин 2) 3) 4) 5) графа. Каждой дуге (i, j) сопоставлен вес С[i, j] - неотрицательное число, все остальные значения С[i, j] = ∞. Вместо значения ∞ необходимо использовать значение, заведомо большее суммарного пути в графе. Переменная flag – логическая переменная (флаг существования пути - имеет значение true, если путь существует, false, если путь не существует) изначально сопоставляется значение true. Линейный массив Length[1. . 6] - предназначен для запоминания суммарного пути от начальной вершины до каждой вершины графа (Length[i] – «вес вершины» ). Вначале программы каждой вершине кроме начальной сопоставляется вес, равный бесконечности, назовем вес временным. Начальной вершине сопоставляем вес равный нулю, назовем вес постоянным. Линейный логический массив Mark[1. . 6], указывает была ли рассмотрена данная вершина (false – была рассмотрена, true – еще не рассматривалась). Переменная u - обозначает рассматриваемую вершину, вначале задать u=s.

Шаг 1 - Обновление весов Перебираем массив Length и рассматриваем вершины, которые не были посещены, т. е. Mark[i]=True и изменяем вес вершины по правилу: Length[i]=min( Length[i], Length[u]+C[u, i]), таким образом будут рассмотрены только те из не посещенных вершин которые являются смежными с текущей. for i: =1 to n do if mark[i] and (length[i]>(length[u]+c[u, i])) then length[i]: = length[u]+c[u, i];

Шаг 2 - Смена текущей вершины В массиве Length[i] анализируем не посещенные вершины (Mark[i]=True) - находим вершину с минимальным весом: min: =255; {начальное значение для поиска минимума в массиве} min_i: =0; {значение индекса минимальной временной вершины } for i: =1 to n do if mark[i] and (length[i]

Шаг 2 - Смена текущей вершины Если вершина с минимальным весом не найдена if min_i=0 then … останавливаем поиск. Произойти это может быть в 2 -х случаях: все вершины уже посещены, либо нет смежных вершин (нет дальше пути - у всех вес равен бесконечности). flag: =false; {выставляем флаг «нет пути из s в t» } u: =t; {досрочный выход из цикла} Если вершина с минимальным весом найдена, то делаем ее постоянной и текущейm mark[min_i]: =false; {помечаем ее как постоянную} u: =min_i; {делаем ее текущей вершиной}

Условия продолжения поиска Шаги 1 и 2 повторяются до тех пор пока u не станет равной t. Длина кратчайшего пути будет равна Length[t]. repeat … until u=t;

Фрагмент алгоритма Дейкстры Repeat {поиск смежных с текущей вершин, и вычисление расстояния от начальной вершины до них } for i: =1 to n do if m[i] and (l[i]>(l[u]+c[u, i])) then l[i]: =l[u]+c[u, i]; {поиск минимальной временной вершины не найдена} min: =255; min_i: =0; for i: =1 to n do if m[i] and (l[i]

Начальные присваивания C - матрица весов дуг 1 2 3 4 5 ∞ 4 ∞ 1 3 ∞ 2 ∞ ∞ 3 ∞ ∞ ∞ ∞ 4 ∞ ∞ 1 2 5 ∞ ∞ 4 ∞ ∞ ∞ 6 ∞ ∞ 2 ∞ ∞ ∞ Length – массив весов вершин Текуща я верши на 6 1 Шаг алго рит ма 2 4 1 3 3 1 1 4 5 2 4 3 2 6 (красный цвет – вес постоянный синий цвет - вес временный) u 1 1 2 3 4 5 6 1 0 ∞ ∞ ∞ ∞ ∞

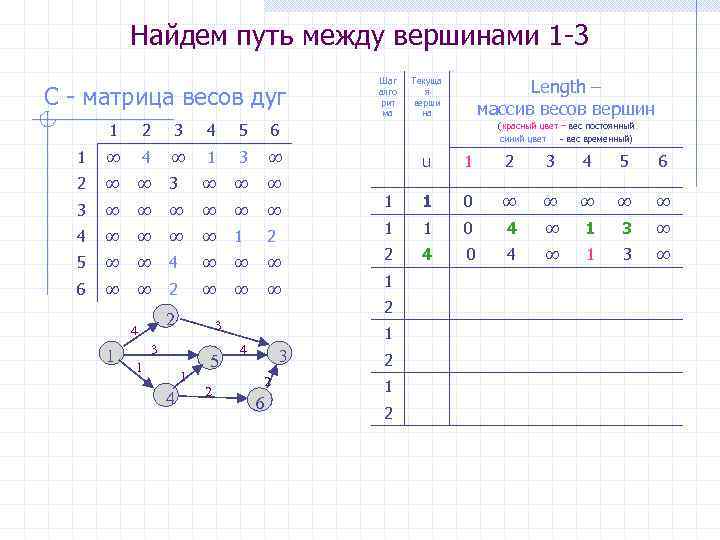Найдем путь между вершинами 1 -3 C - матрица весов дуг 1 2 3 4 5 ∞ 4 ∞ 1 3 ∞ 2 ∞ ∞ 3 ∞ ∞ ∞ ∞ 4 ∞ ∞ 1 2 5 ∞ ∞ 4 ∞ ∞ ∞ 6 ∞ ∞ 2 ∞ ∞ ∞ Length – массив весов вершин Текуща я верши на 6 1 Шаг алго рит ма 2 4 1 3 3 1 1 4 5 2 (красный цвет – вес постоянный синий цвет - вес временный) u 1 2 3 4 5 6 1 1 0 ∞ ∞ ∞ ∞ ∞ 1 1 0 4 ∞ 1 3 ∞ 2 4 0 4 ∞ 1 3 ∞ 1 2 1 4 3 2 6 2 1 2

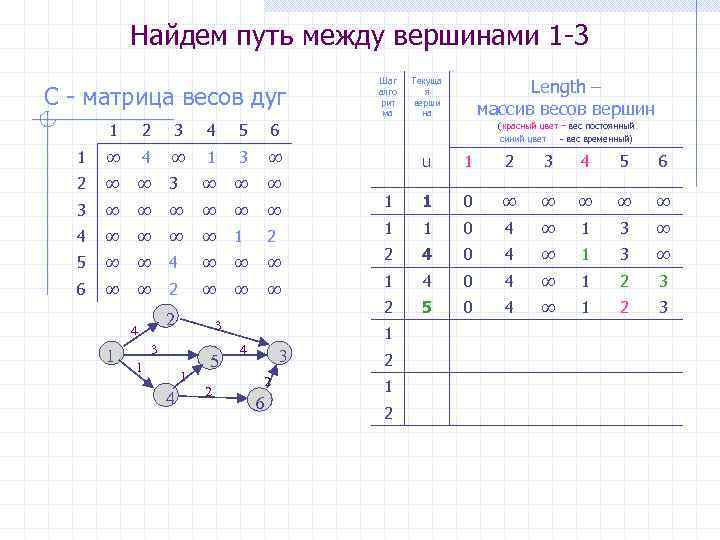Найдем путь между вершинами 1 -3 C - матрица весов дуг 1 2 3 4 5 ∞ 4 ∞ 1 3 ∞ 2 ∞ ∞ 3 ∞ ∞ ∞ ∞ 4 ∞ ∞ 1 2 5 ∞ ∞ 4 ∞ ∞ ∞ 6 ∞ ∞ 2 ∞ ∞ ∞ Length – массив весов вершин Текуща я верши на 6 1 Шаг алго рит ма 2 4 1 3 3 1 1 4 5 2 (красный цвет – вес постоянный синий цвет - вес временный) u 1 2 3 4 5 6 1 1 0 ∞ ∞ ∞ ∞ ∞ 1 1 0 4 ∞ 1 3 ∞ 2 4 0 4 ∞ 1 3 ∞ 1 4 0 4 ∞ 1 2 3 2 5 0 4 ∞ 1 2 3 1 4 3 2 6 2 1 2

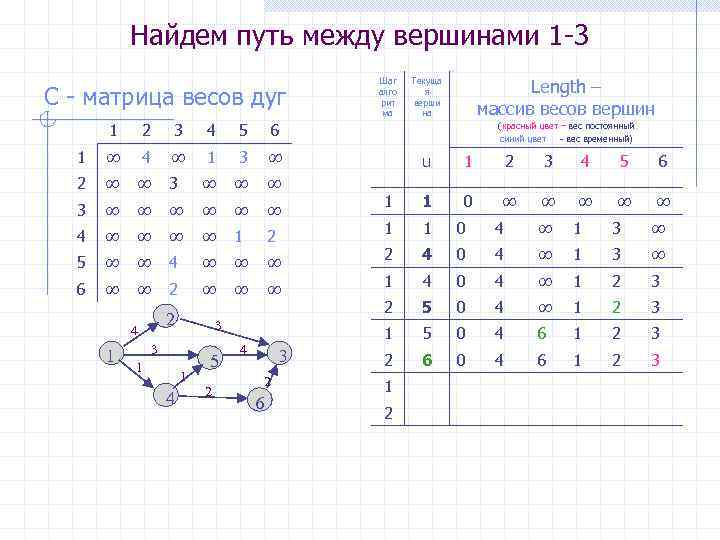Найдем путь между вершинами 1 -3 C - матрица весов дуг 1 2 3 4 5 ∞ 4 ∞ 1 3 ∞ 2 ∞ ∞ 3 ∞ ∞ ∞ ∞ 4 ∞ ∞ 1 2 5 ∞ ∞ 4 ∞ ∞ ∞ 6 ∞ ∞ 2 ∞ ∞ ∞ Length – массив весов вершин Текуща я верши на 6 1 Шаг алго рит ма 2 4 1 1 1 4 5 2 4 3 2 6 u 1 2 3 4 5 6 1 1 0 ∞ ∞ ∞ ∞ ∞ 1 1 0 4 ∞ 1 3 ∞ 2 4 0 4 ∞ 1 3 ∞ 1 4 0 4 ∞ 1 2 3 2 5 0 4 ∞ 1 2 3 1 3 3 (красный цвет – вес постоянный синий цвет - вес временный) 5 0 4 6 1 2 3 2 6 0 4 6 1 2 3 1 2

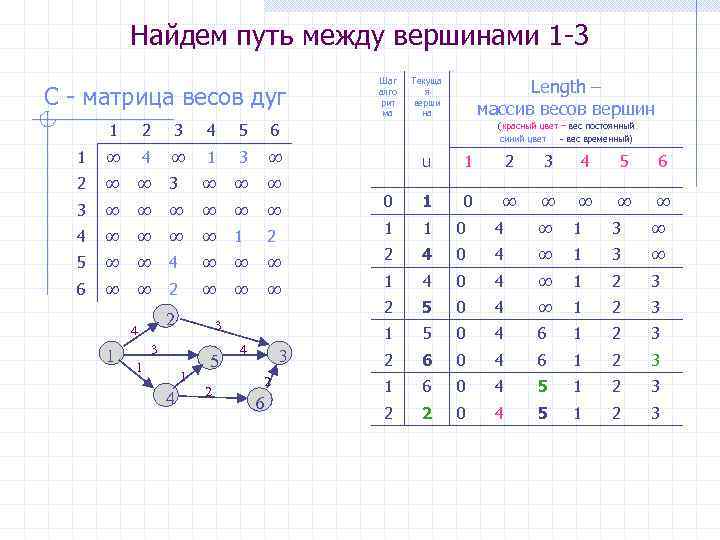Найдем путь между вершинами 1 -3 C - матрица весов дуг 1 2 3 4 5 ∞ 4 ∞ 1 3 ∞ 2 ∞ ∞ 3 ∞ ∞ ∞ ∞ 4 ∞ ∞ 1 2 5 ∞ ∞ 4 ∞ ∞ ∞ 6 ∞ ∞ 2 ∞ ∞ ∞ Length – массив весов вершин Текуща я верши на 6 1 Шаг алго рит ма 2 4 1 1 1 4 5 2 4 3 2 6 u 1 2 3 4 5 6 0 1 0 ∞ ∞ ∞ ∞ ∞ 1 1 0 4 ∞ 1 3 ∞ 2 4 0 4 ∞ 1 3 ∞ 1 4 0 4 ∞ 1 2 3 2 5 0 4 ∞ 1 2 3 1 3 3 (красный цвет – вес постоянный синий цвет - вес временный) 5 0 4 6 1 2 3 2 6 0 4 6 1 2 3 1 6 0 4 5 1 2 3 2 2 0 4 5 1 2 3

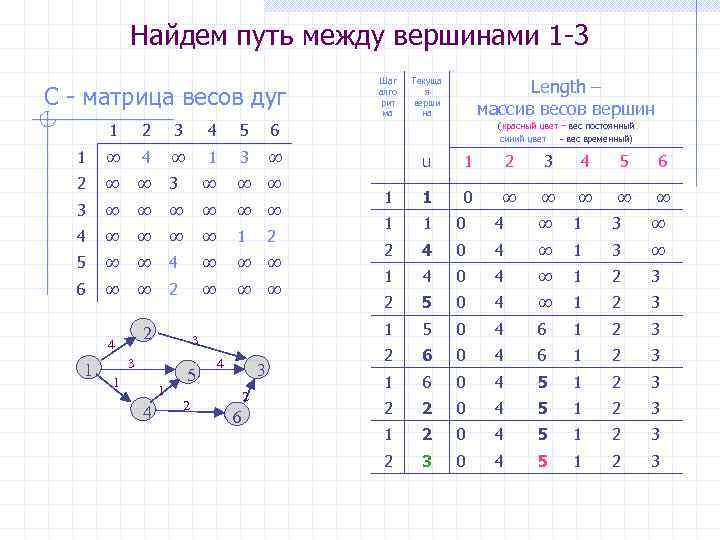Найдем путь между вершинами 1 -3 C - матрица весов дуг 1 2 3 4 5 ∞ 4 ∞ 1 3 ∞ 2 ∞ ∞ 3 ∞ ∞ ∞ ∞ 4 ∞ ∞ 1 5 ∞ ∞ 4 ∞ ∞ ∞ 6 ∞ ∞ 2 ∞ ∞ ∞ Length – массив весов вершин Текуща я верши на 6 1 Шаг алго рит ма 2 4 1 1 1 4 5 2 4 3 2 6 u 1 2 3 4 5 6 1 1 0 ∞ ∞ ∞ ∞ ∞ 1 1 0 4 ∞ 1 3 ∞ 2 4 0 4 ∞ 1 3 ∞ 1 4 0 4 ∞ 1 2 3 2 5 0 4 ∞ 1 2 3 3 (красный цвет – вес постоянный синий цвет - вес временный) 5 0 4 6 1 2 3 2 6 0 4 6 1 2 3 1 6 0 4 5 1 2 3 2 2 0 4 5 1 2 3 1 2 0 4 5 1 2 3

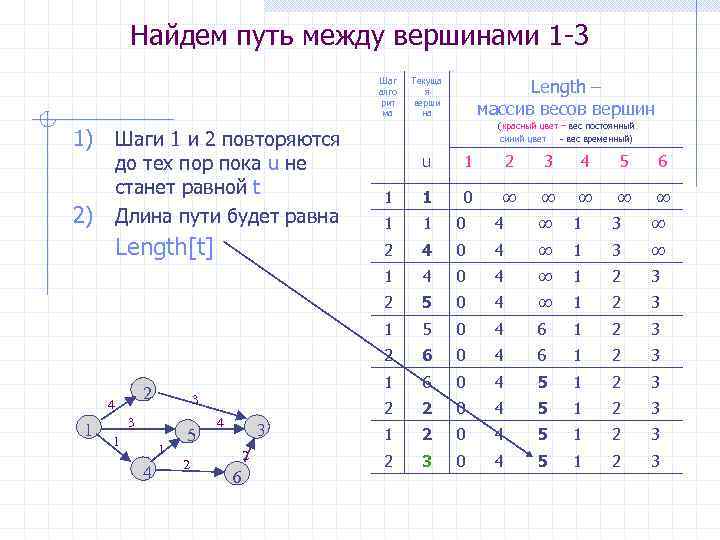Найдем путь между вершинами 1 -3 Шаг алго рит ма Length – массив весов вершин Текуща я верши на (красный цвет – вес постоянный синий цвет - вес временный) 1) Шаги 1 и 2 повторяются до тех пор пока u не станет равной t Длина пути будет равна 1 1 1 4 5 2 3 2 6 1 1 0 ∞ ∞ ∞ ∞ ∞ 1 1 0 4 ∞ 1 3 ∞ 4 0 4 ∞ 1 2 3 5 0 4 6 1 2 3 6 0 4 5 1 2 3 2 4 6 1 3 5 2 3 4 1 4 3 2 2 Length[t] 1 1 2) u 2 0 4 5 1 2 3 1 2 0 4 5 1 2 3

Выделение кратчайшего пути Для указания через какие вершины проходит кратчайший путь используют метод «выделение пути обратным ходом» : 1) 2) 3) назначить текущей вершиной конечную вершину; для каждой вершины, связанной с ней заходящими дугами, определить разность между весом текущей вершины и весом дуги. Вершину, вес которой совпадает с этой разницей, назовем текущей, а вес отнесем к пути. Повторить пункт 2 до тех пор, пока текущей не станет 1 2 3 4 5 6 начальная вершина. 2 3 4 1 u: =t; write(u); 3 4 1 3 5 2 1 repeat 1 2 3 2 for j: =1 to n do 4 6 4 if l[u]-l[j]=c[j, u] then begin 5 u: =j; 6 write(u); end; until u=s; ∞ 4 ∞ 1 3 ∞ ∞ ∞ ∞ 1 2 ∞ ∞ 4 ∞ ∞ ∞ 2 ∞ ∞ ∞