ПОГРЕШНОСТИ План лекции: • Классификация погрешностей. • Расчёт

ПОГРЕШНОСТИ План лекции: • Классификация погрешностей. • Расчёт погрешностей прямых и косвенных измерений. • Примеры расчёта погрешностей измерений медико-биологической величины.

Обработка результатов исследования, составление методик для проведения терапевтических, профилактических процедур и их анализа, требует от современного медика владения элементарными навыками физического эксперимента и обработки полученных результатов.

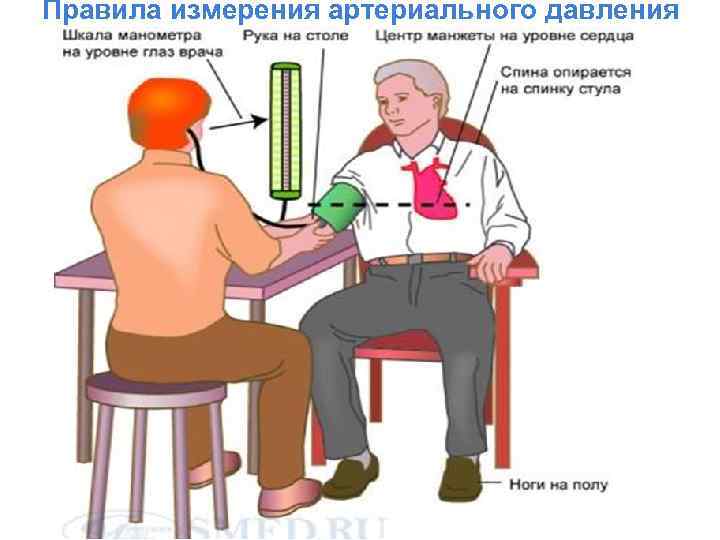Правила измерения артериального давления

Результаты эксперимента дают количественную оценку явления и по степени точности можно судить о близости полученных значений к истинному значению величины. Получить само истинное значение измеряемой величины невозможно, т. к. всякое измерение сопровождается определённой ошибкой - погрешностью измерений.

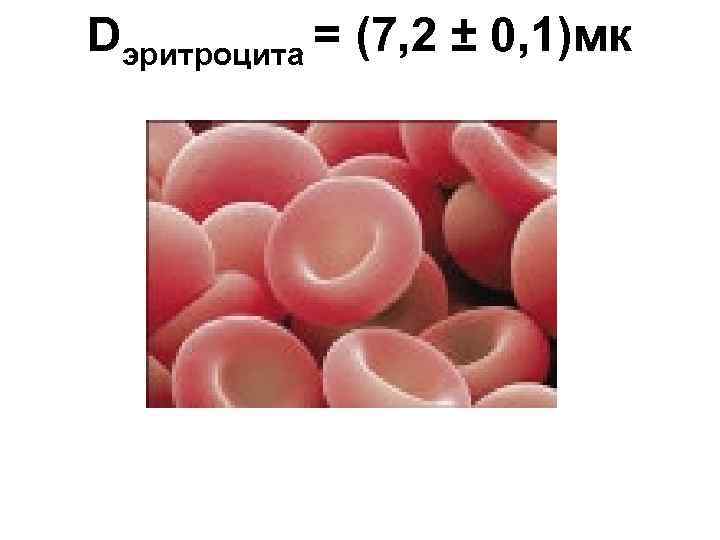Dэритроцита = (7, 2 ± 0, 1)мк

Различают три вида погрешностей: • систематические • случайные • промахи

Систематические погрешности при любых измерениях либо уменьшают, либо увеличивают результат. 0 ни могут быть учтены путём поправок на воздействие внешних факторов и при сопоставлении результатов измерений с показаниями эталонного прибора.

В паспорте прибора указаны поправки, которые необходимо учесть при записи результата измерений, (поправки учитывают влияние перепада температур, влажности, давления, электромагнитных полей и т. д. ).

Систематические погрешности возникают применении приближённых уравнений и констант. Систематические погрешности выявляются и устраняются.

Случайные погрешности основаны на неточностях, которые невольно допускает экспериментатор: (пылинка на чаше аналитических весов, трамвай вибрация ошибка)

Случайные погрешности подчиняются законам математической статистики, - нормальному закону. Вычисляются и учитываются в ответе.

Грубые погрешности, или промахи возникают по вине экспериментатора: неаккуратности и невнимательности. Эти ошибки выявляются при повторных измерениях и устраняются.

Теория погрешностей, используя теорию вероятностей, позволяет уменьшить влияние величины случайных погрешностей на окончательный результат измерений.

Измерения • Прямые измерения (по прибору). • Косвенные измерения (по формуле)

Погрешность непосредственных прямых измерений.

Пусть х1 , х2 , х3, ……. . хn - результаты прямых измерений Результат каждого измерения обозначим хi где i меняется oт 1 до n, где n -общее число измерений.

Каждое измеренное значение отличается от истинного значения на величину, представляющую погрешность отдельного измерения.

План обработки данных опыта:

1. Определить среднее арифметическое значение

2. Найти абсолютную погрешность каждого измерения: i = 1, 2, . . . . n

3. Вычислить квадраты абсолютных погрешностей -

4. Определить среднеквадратическую погрешность Sх:

5. Найти абсолютную погрешность всех измерений

доверительная вероятность - коэффициент Стьюдента, - где n - число измерений. 0, 95 для лабораторных работ

коэффициент Стьюдента определяется по таблице или 95 %, т. е. 95% результатов от общего числа учтено в представленном ответе – доверительном интервале.

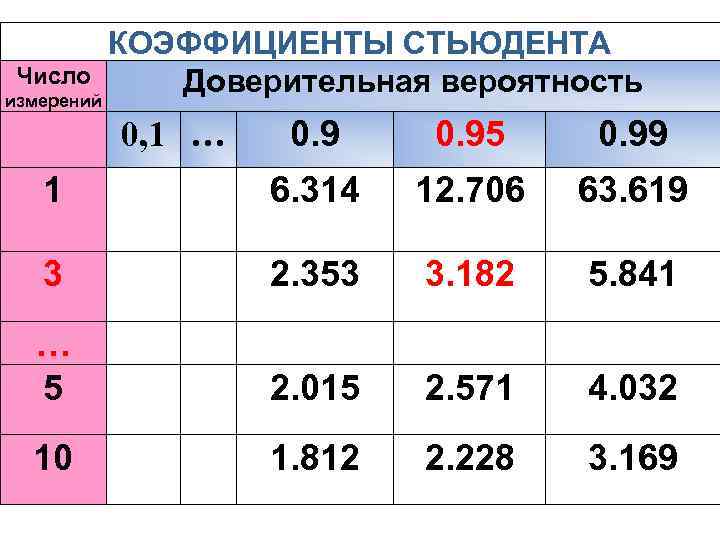КОЭФФИЦИЕНТЫ СТЬЮДЕНТА Число Доверительная вероятность измерений 0. 95 0. 99 1 6. 314 12. 706 63. 619 3 2. 353 3. 182 5. 841 … 5 2. 015 2. 571 4. 032 10 1. 812 2. 228 3. 169 0, 1 …

Коэффициент Стьюдента необходим для определения абсолютной погрешности всех измерений: , что позволяет найти доверительный интервал ( ).

6. Записать результаты измерения в виде: доверительный интервал

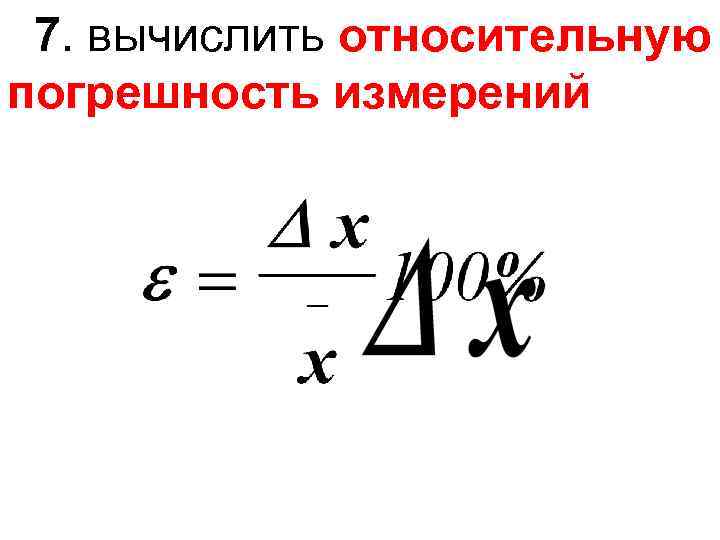7. вычислить относительную погрешность измерений

Для лабораторных исследований ε≤ 5%

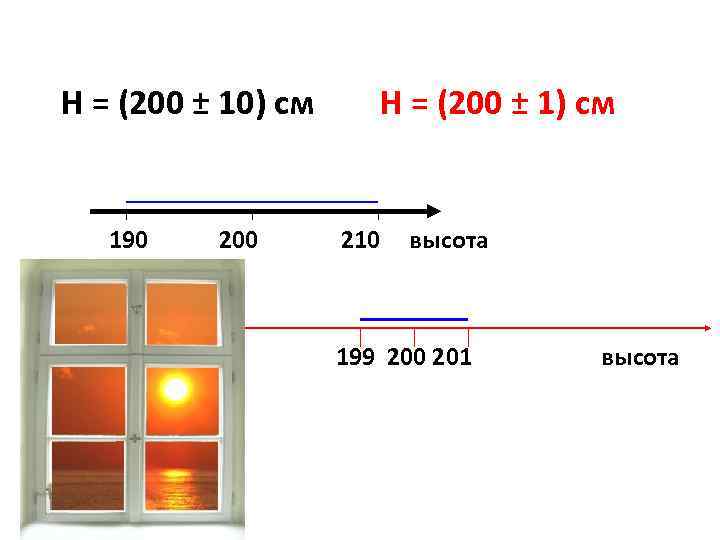H = (200 ± 10) см H = (200 ± 1) см 190 200 210 высота 199 200 201 высота

H = (200 ± 10) см H = (200 ± 1) см ε = (10/200)× 100% = 5% ε = (1/200)× 100% = 0, 5%

Чем точнее выполнены измерения, тем меньше абсолютная погрешность, тем меньше разброс значений (Sx), тем острее вершина кривой Гаусса. H = (200 ± 10) см H = (200 ± 1) см 190 200 210 высота 199 200 201 высота

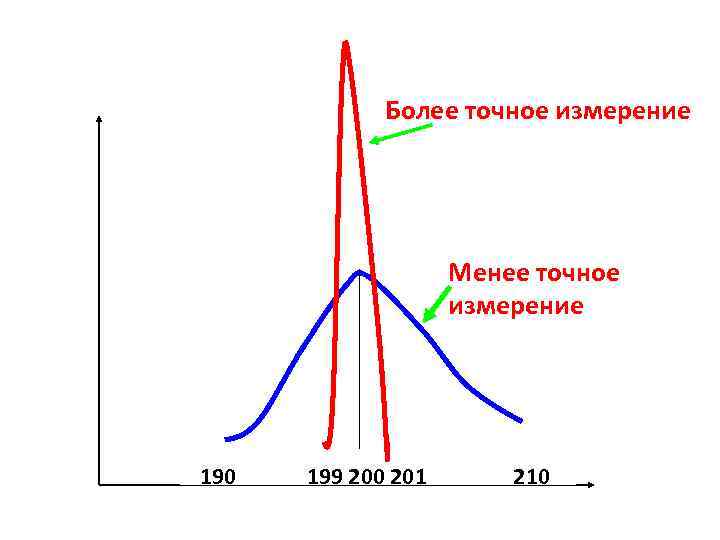Более точное измерение Менее точное измерение 190 199 200 201 210

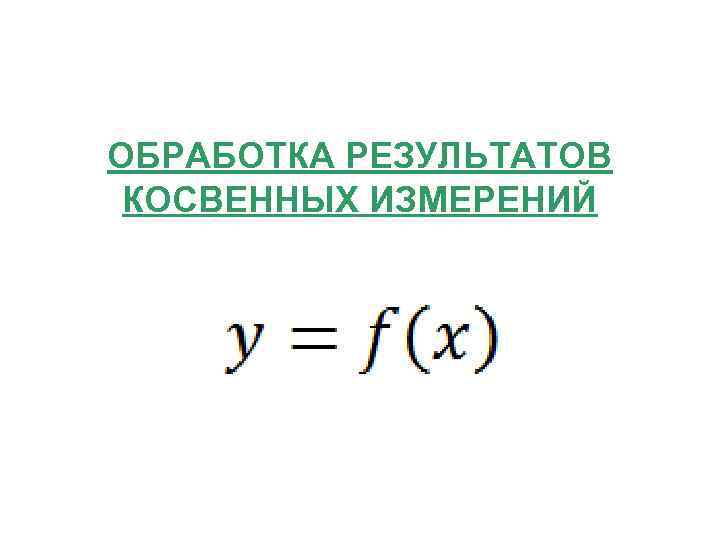ОБРАБОТКА РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ

Пусть - функциональная зависимость.

1. Для оценки погрешностей необходимо: Определить среднее арифметическое этой функции используя средние значения

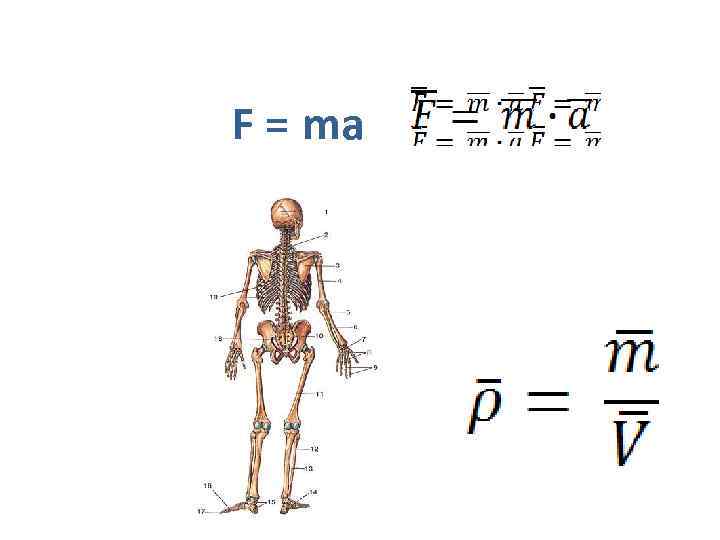F = ma

2. Вычислить среднеквадратическую погрешность косвенной величины Sy:

где - частные производные функции, среднеквадратические погрешности прямых измерений.

3. Найти абсолютную погрешность косвенно определяемой величины коэффициент Стьюдента. Определяют по таблице.

4. Записать результат косвенных измерений в виде: доверительный интервал

• Указать относительную погрешность

ПРИБОРНАЯ ПОГРЕШНОСТЬ При однократных измерениях по электроизмерительному прибору необходимо учитывать класс точности прибора. амперметры, вольтметры, термометры, манометры и др.

. . 0, 05; 1; Электроизмерительные приборы по степени точности делятся на 8 клaccoв: 0, 1; 1, 5; 0, 2; 0, 5; 2, 5; 4.

Число, указывающее класс точности прибора, обозначает его относительную погрешность, выраженную в процентах. Класс точности прибора. обозначается: γ

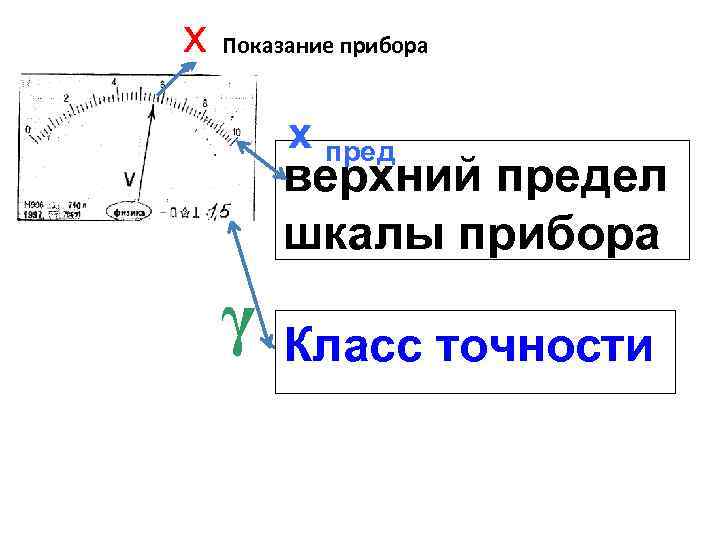х Показание прибора х пред верхний предел шкалы прибора γ Класс точности

Зная класс точности прибора γ и верхний предел шкалы прибора (номинальное значение) хн или (х пред )можно найти абсолютную погрешность прибора.

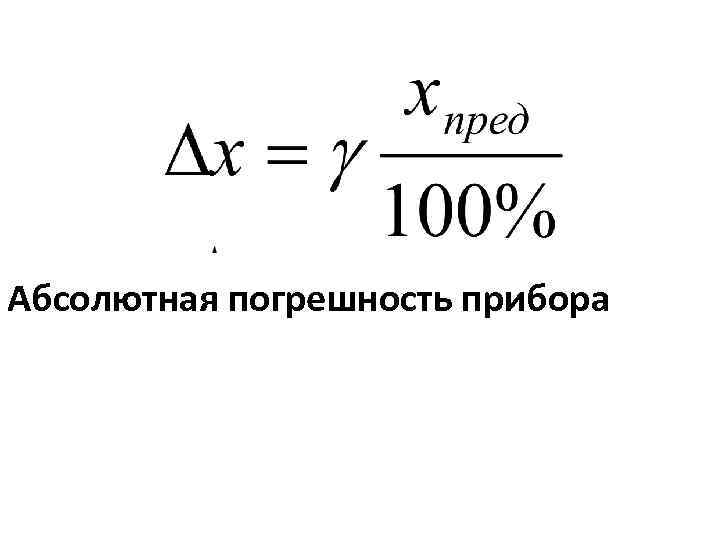Абсолютная погрешность прибора

Относительная погрешность отдельного измерения равна произведению класса точности прибора на отношение номинальной величины хн (хпред. ) к измеренной х.

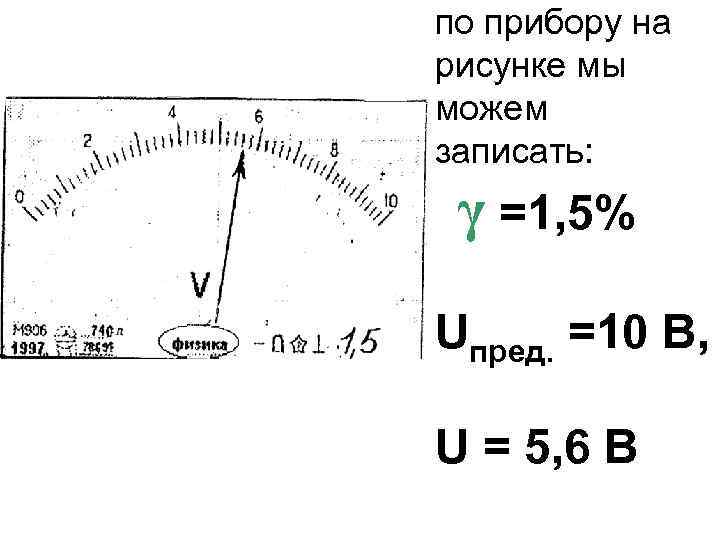по прибору на рисунке мы можем записать: γ =1, 5% Uпред. =10 В, U = 5, 6 B

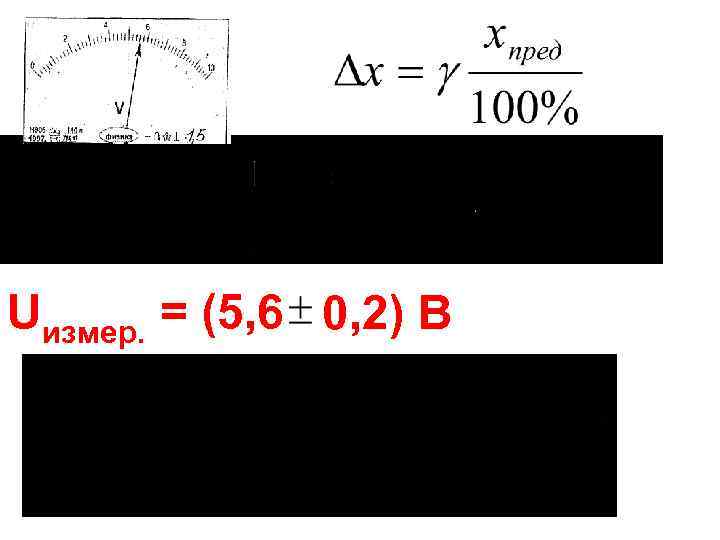Uизмер. = (5, 6 0, 2) В

результат соответствует пределу допустимой погрешности: ≤ 5%

ПОЧЕМУ прибор с классом точности 1, 5% даёт погрешность 3, 6 %?

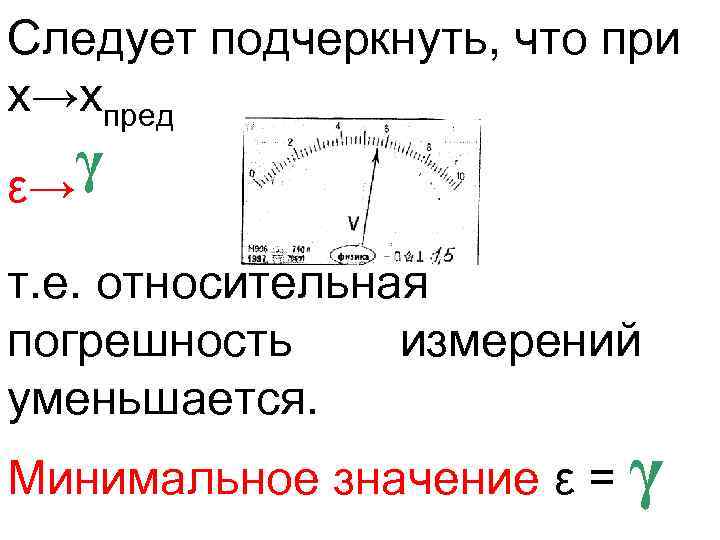Следует подчеркнуть, что при х→хпред γ ε→ т. е. относительная погрешность измерений уменьшается. Минимальное значение ε = γ

В тех случаях, когда нет класса точности, абсолютная погрешность принимается равной цене деления прибора или половине цены наименьшего деления.

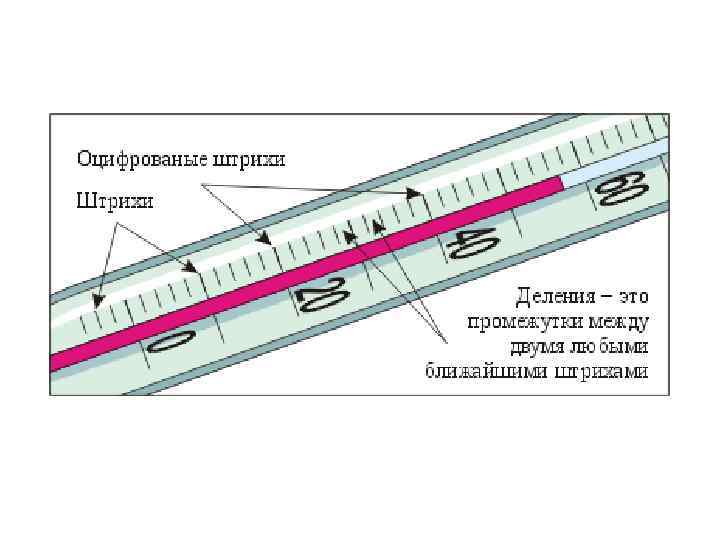
Например, при. измерении температуры термометром, наименьшее деление которого 0, 1°С, допускается ошибка 0, 05 °С, при измерении линейкой, наименьшее деление которой 1 мм, допускается ошибка 0, 5 мм.

Цифровые приборы АБСОЛЮТНАЯ погрешность равна наименьшему разряду

Цифровой амперметр

В автоматических приборах измерение погрешности обычно производится сравнением показателей автоматического тонометра с результатами прослушивания тонов Короткова. Одновременно измеряется верхнее и нижнее Кровяное давление механическим способом и автоматическим. Полученные результаты сравниваются. Сравнения производятся многократно.

Глюкометр Richtest GM-300 применяют для измерение глюкозы в крови Многофункциональный измеритель электрических параметров METREL MI 3102

Какая информация представлена в данном доверительном интервале? Хизм = 25, 6 кг ± 0, 4%

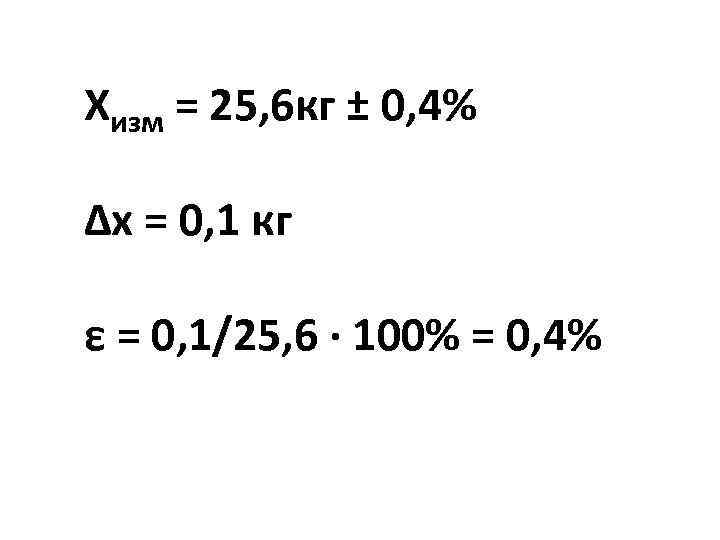Хизм = 25, 6 кг ± 0, 4% Δх = 0, 1 кг ε = 0, 1/25, 6 · 100% = 0, 4%