Пограничный слой.ppt
- Количество слайдов: 17

Пограничный слой В. А. Aлексин Институт проблем механики РАН, МГИУ

Введение С увеличением числа Рейнольдса возникает неустойчивость течения, которая характеризуется возникновением пульсаций газодинамических параметров. Начинается процесс перехода ламинарного режима течения в турбулентный. Турбулентный режим течения носит ярко выраженный хаотический, неупорядочный характер изменения параметров во времени и в пространстве. Предполагается, что турбулентные течения описываются системой вязких уравнений (Навье-Стокса). Ламинарное (слоистое) движение. Турбулентность означает: возбуждение, сморщивание, возмущение (словарь Вебстера). Турбулентное движение жидкости предполагает наличие неупорядочности течения, в котором различные величины претерпевают хаотическое изменение по времени и пространственным координатам и при этом могут быть выделены статистически точные их осредненные значения (И. О. Хинце, 1959).

Теория ламинарного пограничного слоя Уравнения Навье- Стокса Уравнение движения имеет вид (1) В проекции на оси декартовой прямоугольной системы координат xi для компонент скорости ui представляется как три скалярных уравнения (i, k=1, 3) (2) Для изотропной линейной вязкой несжимаемой жидкости по закону Навье-Стокса выполнены соотношения ( V=0)
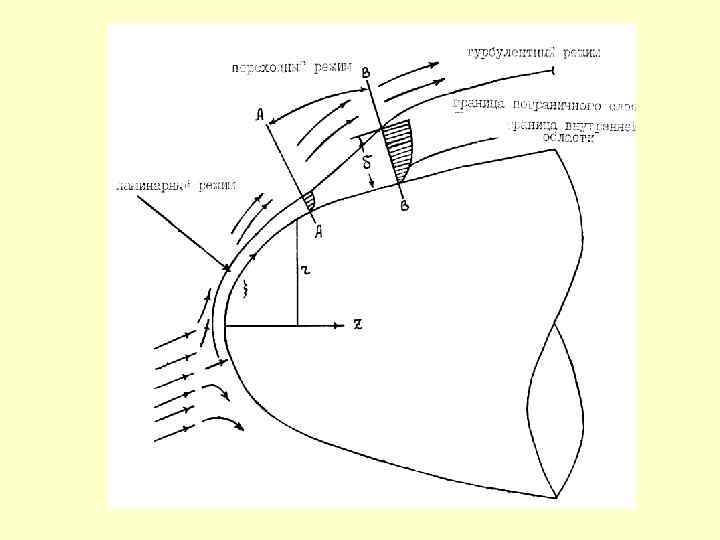

Теория ламинарного пограничного слоя Оценка членов уравнений движения Продольное обтекание плоской пластины потоком несжимаемой жидкости. Скорость в декартовой прямоугольной системе координат, связанной с поверхностью пластины: =x 1, =x 2 ( - по потоку и вдоль поверхности, - по нормали к поверхности u=u 1, v=u 2 Уравнения плоского стационарного течения в системе координат , , связанной с поверхностью пластины (3) (4)

Теория ламинарного пограничного слоя Оценка членов уравнений движения Предполагая, что толщина пограничного слоя по отношению к длине пластины l – величина малая, т. е. , , 1, (5) получим оценки для характеристик плоскопараллельного движения в слое толщиной вблизи поверхности , (6) Из оценок (6) можно сделать вывод, что производные первого и второго порядков от продольной компоненты скорости u удовлетворяют неравенствам , (7)

Теория ламинарного пограничного слоя Оценка членов уравнений движения Из уравнения неразрывности следует (8) Из оценки (8) следует малость нормальной компоненты скорости по сравнению с продольной составляющей. В первом уравнении движения (4) конвективные члены в левой части имеют одинаковый порядок и он совпадает с порядком второго вязкого члена (10) Порядок первого вязкого члена много меньше порядка остальных при больших числах Рейнольдса Rel ,

Теория ламинарного пограничного слоя Оценка членов уравнений движения Тогда из (10) получается выражение для оценки толщины пограничного слоя , (11) Определим порядки членов второго уравнения движения (4) на координату (12) Порядок первого члена правой части (с давлением) определяется порядком последнего вязкого члена и конвективных членов в левой части, равным , который мал по сравнению с порядком члена с давлением в первом уравнении. Следовательно, и от уравнения (4) остается (13)

Теория ламинарного пограничного слоя Оценка членов уравнений движения Следовательно, p=p( ) В первом уравнении движения, опуская только первый вязкий член, получаем уравнение пограничного слоя (14) которое дополняется уравнением неразрывности (3). На внешней границе пограничного слоя при больших , где вязкий и второй конвективный члены малы, предполагается выполнение асимптотического условия В результате уравнение (14) переписывается в форме (15)

Теория ламинарного пограничного слоя Задача Блазиуса II. Неограниченная пластина(или стенка) начинает двигаться из состояния покоя с постоянной скоростью -U 0 в отрицательном направлении оси x. Жидкость вовлекается в движение слоями за счет сил вязкости. Отсутствует продольный характерный размер вдоль x. Тогда скорость жидкости зависит только от t и y Уравнение неразрывности удовлетворяется тождественно, уравнение движения имеет вид (1) Начальные и граничные условия (2) При t>0

Теория ламинарного пограничного слоя Задача Блазиуса II. Решение. Независимые параметры задачи: t, y, = / Тогда безразмерная комбинация из них: (3) (4) Решение Окончательное решение Обратим движение жидкости , полагая V =-U 0

Теория ламинарного пограничного слоя Задача Блазиуса I. Обтекания плоской пластинки. (5) (6) Решение. Независимые параметры задачи: U 0, x, y, = / Тогда безразмерные комбинации из них: , ( 7) Если вместо x , y ввести , (8) , Решение не зависит от L, только от второго аргумента

Теория ламинарного пограничного слоя Задача Блазиуса I. Обтекания плоской пластинки. (9) Решение. Если ввести функцию тока (10) Окончательно уравнение Решение

Boundary Layer Boundary layers were first postulated by Prandtl in 1904. The boundary layer can be seen in this picture of flow over a flat plate. Hydrogen bubbles are released periodically and are carried by the fluid. You can see from the profile that the fluid speed near the plate. . . in the boundary layer. . . is slower than in the freestream.
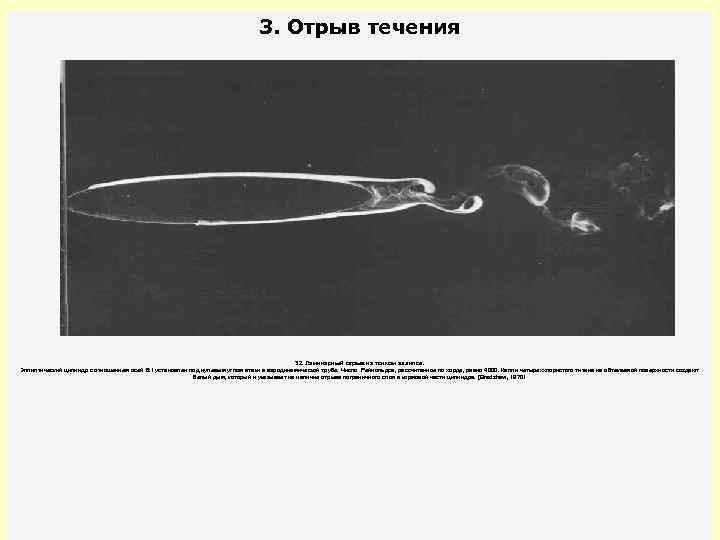
3. Отрыв течения 32. Ламинарный отрыв на тонком эллипсе. Эллиптический цилиндр с отношением осей 6: 1 установлен под нулевым углом атаки в аэродинамической трубе. Число Рейнольдса, рассчитанное по хорде, равно 4000. Капли четыреххлористого титана на обтекаемой поверхности создают белый дым, который и указывает на наличие отрыва пограничного слоя в кормовой части цилиндра. [Bradshaw, 19701

Система уравнений двумерного пограничного слоя несжимаемой жидкости относительно координат ,

= e(h/he) , = 0. 75, Граничные условия задаются на поверхности обтекаемого тела и на внешней границе пограничного слоя, где известны данные невязкого течения
Пограничный слой.ppt