 Подпространства линейного пространства
Подпространства линейного пространства
 Подпространства и подмножества Определение. Подмножество W линейного пространства V называется линейным подпространством, если оно является линейным пространством относительно операций из V. Обозначение. Утверждение. (ноль принадлежит любому подпространству) Утверждение. Для любого линейного пространства V подмножества {0} и V являются подпространствами.
Подпространства и подмножества Определение. Подмножество W линейного пространства V называется линейным подпространством, если оно является линейным пространством относительно операций из V. Обозначение. Утверждение. (ноль принадлежит любому подпространству) Утверждение. Для любого линейного пространства V подмножества {0} и V являются подпространствами.
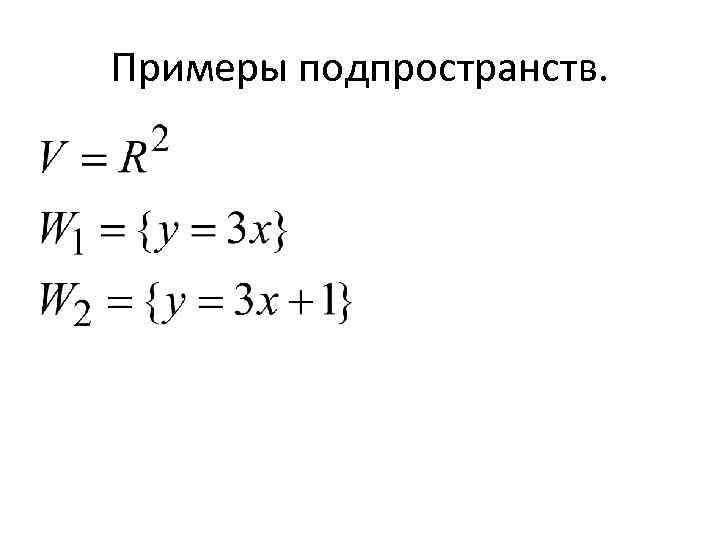 Примеры подпространств.
Примеры подпространств.
 Равносильное определение. Утверждение. Множество W является линейным подпространством V тогда и только тогда, когда оно замкнуто относительно операций сложения и умножения на число:
Равносильное определение. Утверждение. Множество W является линейным подпространством V тогда и только тогда, когда оно замкнуто относительно операций сложения и умножения на число:
 Подпространства матриц Пусть W 1 – симметрические матрицы W 2 – кососимметрические матрицы
Подпространства матриц Пусть W 1 – симметрические матрицы W 2 – кососимметрические матрицы
![Подпространства C[a, b] Пусть V=C[a, b] – пространство непрерывных функций на отрезке [a, b] Подпространства C[a, b] Пусть V=C[a, b] – пространство непрерывных функций на отрезке [a, b]](https://present5.com/presentation/1/-57835816_281059462.pdf-img/-57835816_281059462.pdf-6.jpg) Подпространства C[a, b] Пусть V=C[a, b] – пространство непрерывных функций на отрезке [a, b]
Подпространства C[a, b] Пусть V=C[a, b] – пространство непрерывных функций на отрезке [a, b]
 Пересечение и объединение подпространств Пусть V – ЛП, W 1, W 2 – подпространства V Определение. Утверждение. Пересечение подпространств является подпространством. Замечание. Объединение подпространств не является подпространством.
Пересечение и объединение подпространств Пусть V – ЛП, W 1, W 2 – подпространства V Определение. Утверждение. Пересечение подпространств является подпространством. Замечание. Объединение подпространств не является подпространством.
 Сумма подпространств Определение. Утверждение. Сумма двух подпространств является подпространством. Замечание. Разложение произвольного вектора из W 1+W 2 по W 1 и W 2 возможно не единственным образом.
Сумма подпространств Определение. Утверждение. Сумма двух подпространств является подпространством. Замечание. Разложение произвольного вектора из W 1+W 2 по W 1 и W 2 возможно не единственным образом.
 Пример суммы подпространств Пример. W 1=XOY W 2=YOZ W 1+W 2=R 3 Поскольку для любого вектора возможно разложение:
Пример суммы подпространств Пример. W 1=XOY W 2=YOZ W 1+W 2=R 3 Поскольку для любого вектора возможно разложение:
 Прямая сумма подпространств Определение. Пространство V называется прямой суммой подпространств W 1 и W 2, если V=W 1+W 2 и любой вектор x представим в виде x=w 1+w 2 единственным образом. Обозначение. Пример. Поскольку разложение единственнно
Прямая сумма подпространств Определение. Пространство V называется прямой суммой подпространств W 1 и W 2, если V=W 1+W 2 и любой вектор x представим в виде x=w 1+w 2 единственным образом. Обозначение. Пример. Поскольку разложение единственнно
 Теорема о размерности Теорема. Пусть V=W 1+W 2. Тогда Доказательство. Пусть e 1, e 2…. ek - базис W 1∩W 2. dim(W 1∩W 2 )=k e 1, e 2…. ek, a 1, a 2…. aℓ - базис W 1, dim. W 1=k+ℓ e 1, e 2…. ek, b 1, b 2…. bm - базис W 2, dim. W 2=k+m Для доказательства теоремы достаточно проверить, что e 1, e 2…. ek, a 1, a 2…. aℓ b 1, b 2…. bm - базис V
Теорема о размерности Теорема. Пусть V=W 1+W 2. Тогда Доказательство. Пусть e 1, e 2…. ek - базис W 1∩W 2. dim(W 1∩W 2 )=k e 1, e 2…. ek, a 1, a 2…. aℓ - базис W 1, dim. W 1=k+ℓ e 1, e 2…. ek, b 1, b 2…. bm - базис W 2, dim. W 2=k+m Для доказательства теоремы достаточно проверить, что e 1, e 2…. ek, a 1, a 2…. aℓ b 1, b 2…. bm - базис V
 Доказательство 1. Проверим, что e 1, e 2…. ek, a 1, a 2…. aℓ b 1, b 2…. bm ЛНЗ система векторов Левая часть последнего равенства принадлежит W 1, правая часть принадлежит W 2, следовательно и левая и правая части принадлежат W 1∩W 2, это значит, что правую часть можно выразить через базис пересечения.
Доказательство 1. Проверим, что e 1, e 2…. ek, a 1, a 2…. aℓ b 1, b 2…. bm ЛНЗ система векторов Левая часть последнего равенства принадлежит W 1, правая часть принадлежит W 2, следовательно и левая и правая части принадлежат W 1∩W 2, это значит, что правую часть можно выразить через базис пересечения.
 Доказательство
Доказательство
 Доказательство
Доказательство
 Доказательство 2. Проверим, что любой вектор из ЛП V линейно выражается через систему e 1, …ek, a 1, …aℓ, b 1…bm. □
Доказательство 2. Проверим, что любой вектор из ЛП V линейно выражается через систему e 1, …ek, a 1, …aℓ, b 1…bm. □
 Теоремы о прямой сумме Теорема 1. Пусть V=W 1+W 2. Тогда и только тогда, когда ноль раскладывается единственным образом: . Теорема 2.
Теоремы о прямой сумме Теорема 1. Пусть V=W 1+W 2. Тогда и только тогда, когда ноль раскладывается единственным образом: . Теорема 2.