Теплопередача-11(подобие).ppt
- Количество слайдов: 53

ПОДОБИЕ И МОДЕЛИРОВАНИЕ ПРОЦЕССОВ КОНВЕКТИВНОГО ТЕПЛООБМЕНА Веников В. А. Теория подобия и моделирование применительно к задачам электроэнергетики. — М. , 1966; Кирпичев М. В. Теория подобия — М. : 1953; Дьяконов Г. К. Вопросы теории подобия в области физико химических процессов. — М. Л. : 1956. Седов Л. И. Методы подобия и размерности в механике. — 7 изд. — М. : 1972; Эйгенсон Л. С. Моделирование. — М. : 1952; Кутателадзе С. С. Анализ подобия и физические модели (Новосибирск: Наука, 1986. - 295 с. ) Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Попытки аналитического решения полной системы уравнений наталкиваются на серьезные трудности. Поэтому большое значение приобретает экспериментальный путь исследования. С помощью эксперимента для определенных значений аргументов можно получить числовые значения искомых переменных и затем подобрать уравнения, описываю щие результата опытов. Однако при изучении столь сложного процесса, как конвективный теплообмен, не всегда легко проводить и опытное исследование.

Для исследования влияния на процесс какой либо одной величины остальные нужно сохранять неизменными, что не всегда возможно или затруднительно из за большого количества переменных. Кроме того, при этом нужно быть уверенным, что результаты, получаемые с помощью какой либо конкретной установки (модели), можно перенести и на другие аналогичные процессы (образец). Эти трудности помогает разрешить теория подобия. С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем так, что число комплексов будет меньше числа величин, из которых составлены эти комплексы. Полученные безразмерные комплексы можно рассматривать как новые переменные. При введении в уравнения безразмерных комплексов число величин под знаком искомой функции формально сокращается, что упрощает исследование физических процессов. Кроме того, новые безразмерные переменные отражают влияние не только отдельных факторов, но и их совокупности, что позволяет легче определить физические связи в исследуемом процессе.

Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому. Ввиду этого теория подобия, прежде всего, является теоретической базой эксперимента, но не только. Теория подобия является важным подспорьем теоретических исследований. Хотя методами теории подобия вид искомой функции не может быть определен, эта теория облегчает в ряде случаев анализ процесса и описание полученных результатов. Для практического использования выводов теории подобия необходимо уметь приводить к безразмерному виду математические описания изучаемых процессов. Имеется несколько методов выполнения этой операции. Мы воспользуемся одним из них методом масштабных преобразований.

ПРИВЕДЕНИЕ МАТЕМАТИЧЕСКОЙ ФОРМУЛИРОВКИ КРАЕВОЙ ЗАДАЧИ К ЗАПИСИ В БЕЗРАЗМЕРНЫХ ПЕРЕМЕННЫХ Пусть поверхность твердого тела омывается несжимаемой жидкостью, температура и скорость которой вдали от тела постоянны и равны соответственно t 0 и 0. Размер тела l 0 задан. Температура поверхности тела равна tc. Для определенности примем, что tc > t 0. Будем полагать, что физические параметры жидкости постоянны (учтем только подъемную силу, возникающую в результате зависимости плотности от температуры). Теплота трения не учитывается. Рассматриваемый процесс является стационарным. Расположим оси координат так, как показано на рис. 5 1. Для простоты примем, что ось Оу нормальна к поверхности тела, а ось Ох направлена вдоль тела и вертикальна.

Рис. 5 1. К постановке краевой задачи конвективного теплообмена. При этом gx = g, а проекции вектора сил тяжести (или подъемной силы) на оси Оу и Oz будут равны нулю (gy=gz=0). Размер тела вдоль оси Oz намного больше l 0. При принятых условиях поля температур и скоростей можно описать дифференциальными уравнениями в приближении пограничного слоя. Учтем дополнительно подъемную силу g , считая ее соизмеримой с вязкостной составляющей . Введем также обозначение = t – t 0 , где t — температура жидкости (заметим, что dt=d так как t 0= const).

Уравнение энергии уравнение движения уравнение сплошности Напишем граничные условия; (а)

В уравнениях и условиях однозначности можно различить три вида величин: независимые переменные — это координаты х, у. зависимые переменные — это зависимые переменные , x, y; однозначно определяются значениями независимых переменных, если заданы величины, входящие в условия однозначности; постоянные величины это 0, t 0, l 0, c, , a, g и др. ; они задаются условиями однозначности и для определенной задачи являются постоянными, но зависящими от других переменных; от задачи к задаче они могут меняться; постоянными эти величины называют потому, что они не являются функцией независимых переменных.

Таким образом, искомые зависимые переменные , x, y; зависят от большого числа величии: они являются функцией независимых переменных и постоянных величин, входящих в условия однозначности. Величины, содержащиеся в уравнениях и условиях однозначности, можно сгруппировать в комплексы. Число безразмерных комплексов будет меньше числа размерных величин. Для приведения к безразмерному виду выберем масштабы приведения. В качестве масштабов удобно принять постоянные величины, входящие в условия однозначности. Для линейных величии выберем какой либо характерный размер, например длину поверхности теплообмена l 0, для скорости 0, для температуры c. Обозначим безразмерные величины: (б) Тогда (в)

Подставим в уравнения значения величин согласно равенствам (в). Преобразуем уравнение энергии. Так как, например. то в результате подстановки равенств (в) после умножения левой и правой частей уравнения энергии на будем иметь: (5. 1) Аналогично преобразуем и уравнение движения. После подстановки равенства (в) в уравнение движения умножим его на . В результате получим:

Сделаем следующее преобразование комплекса, входящего в последнее уравнение: Учитывая эти преобразования, окончательно получаем: (5. 2) После преобразования уравнения сплошности получим: или так как 0/ l 0 не равно нулю. (5. 3)

Приводя к безразмерному виду граничные условия, получаем: (г) Из условии (г) следует, что, несмотря на то, что величины 0, tс, t 0 и др. , входящие в размерные граничные условия, могут иметь различные числовые значения, каждая из безразмерных величин 0, с и др. имеет в рассматриваемом случае вполне конкретное числовое значение. При известном температурном поле коэффициент теплоотдачи может бытъ определен по уравнению Приводя к записи в безразмерных переменных, получаем: (5. 4) Безразмерный комплекс l 0/ полностью определяется производной .

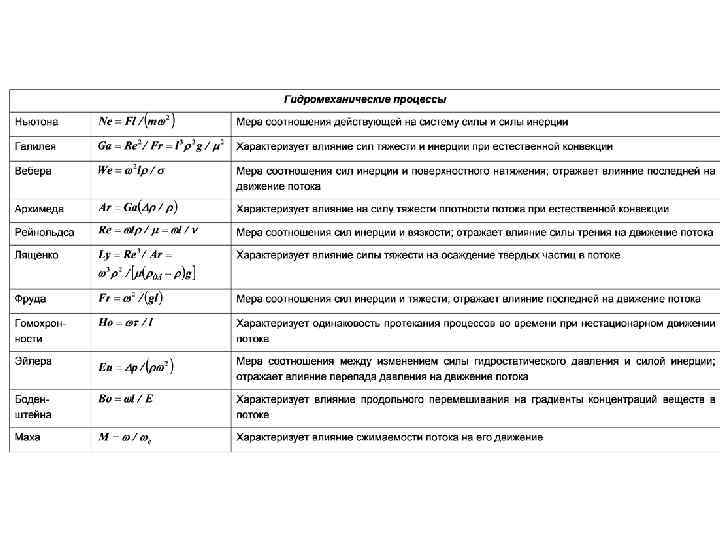
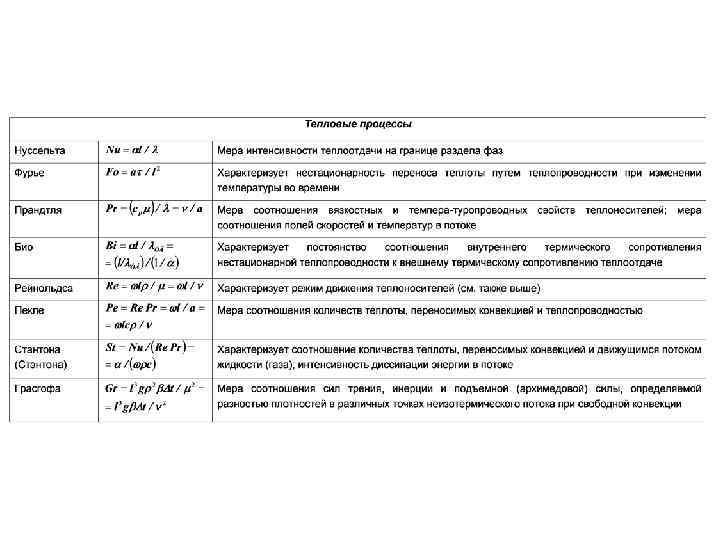
БЕЗРАЗМЕРНЫЕ ПЕРЕМЕННЫЕ (ЧИСЛА ПОДОБИЯ) И УРАВНЕНИЯ ПОДОБИЯ Помимо безразмерных величин , WX, Wy и безразмерных координат, составленных из однородных физических величин, в уравнения входят также безразмерные комплексы, состоящие из разнородных физических величин: Этим комплексам, называемым числами подобия, присвоены имена ученых, внесших значительный вклад в развитие гидродинамики или теплопередачи. Первый из этих безразмерных комплексов обозначают (5. 5) и называют числом Нуссельта или безразмерным коэффициентом теплоотдачи. Число Нуссельта характеризует теплообмен на границе стенка — жидкость; это следует из уравнений. В задачах конвективного теплообмена число Nu обычно является искомой величиной, поскольку в него входит определяемая величина .

Несмотря па внешнее сходство с числом Био, число Нуссельта существенно отличается от него. В число Вi входит коэффициент теплопроводности твердого тела; в число Nu — коэффициент теплопроводности жидкости. Кроме того, в число Био коэффициент теплоотдачи вводится как величина, заданная в условиях однозначности, мы же рассматриваем коэффициент теплоотдачи, входящий в Nu, как величину искомую. Безразмерный комплекс (5. 6) называют числом Рейнольдса. Оно характеризует соотношение сил инерции и сил вязкости. Действительно, число Рейнольдса будет получено, если член уравнения движения, учитывающий инерционные силы, разделить на выражение, учитывающее в этом уравнении силы трения: По существу такую же операцию мы проделали ранее приведении уравнения движения к безразмерному виду.

Число Рейнольдса является важной характеристикой как изотермического, так и неизотермического процессов течения жидкости. Третий безразмерный комплекс обозначают (5. 7) и называют числом Пекле. Его можно преобразовать следующим образом: здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель— теплоту, переносимую теплопроводностью. Ранее получили число Пекле путем деления конвективной части уравнения на выражение, учитывающее перенос теплоты теплопроводностью.

Безразмерный комплекс называют числом Грасгофа. Оно характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей. Вместо Gr можно написать его более общую модификацию — число Архимеда: (5. 9) В случае однородной среды при условии = const число Архимеда идентично числу Gr. Используя введенные обозначения, систему безразмерных дифференциальных уравнений можно записать в следующем виде: (5. 10) (5. 11)

(5. 12) (5. 13) Система безразмерных дифференциальных уравнений и безразмерных условий однозначности (г) представляет собой математическую формулировку задачи. Безразмерные величины , WX, Wy, X, Y, Nu, Re, Ре, Gr можно рассматривать как новые переменные. Их можно разделить на три группы: независимые переменные — это безразмерные координаты X, Y; зависимые переменные — это Nu, , Wx, Wy; они однозначно определяются значениями независимых переменных при определенных значениях величии, входящих в условия однозначности; постоянные величины — это Ре, Re, Gr; они заданы условиями однозначности и для конкретной задачи являются постоянными. Действительно, как следует из (5 6)—(5 8), числа Ре, Re и Gr состоят только из величин, входящих в условия задачи.

В результате можно написать: (5. 14) (5. 15) (5. 16) (5. 17) Уравнения вида (5 14)—(5 17) называют уравнениями подобия. Здесь Xс, Yс — уравнение (5 14)—соответствуют поверхности теплоотдачи (стенки). Нахождение (или Nu) для точек пространства, не лежащих на поверхности стенки, не имеет смысла. В рассматриваемой задаче Yс=0. Если в уравнении движения учесть составляющую то в результате приведения к безразмерной записи появилась бы и составляющая

Безразмерный комплекс (5. 18) называют числом Эйлера. Это число характеризует соотношение сил давления и сил инерции. В уравнения конвективного теплообмена зависимая переменная Еu входит только под знаком производной. Следова тельно, для рассматриваемой нами несжимаемой жидкости с постоянными физическими параметрами существенно не абсолютное значение давления, а его изменение (В случае сжимаемых течений нужно учитывать зависимость плотности от давления; в этом случае представляет интерес абсолютная величина давления). Поэтому число Эйлера обычно представляют в виде где p 0— какое либо фиксированное значение давления, например давление на входе в канал. Это давление может быть неизвестной величиной.

Для многих процессов течения и теплоотдачи существен не только размер l 0, но и некоторые другие характерные размеры. Например, при движении жидкости в прямой гладкой трубе характерными размерами являются диаметр и длина трубы; если труба изогнута, то дополнительным характерным размером является радиус кривизны трубы. При течении жидкости в шероховатых трубах представляют интерес размеры, оценивающие высоту неровностей и их концентрацию на поверхности теплообмена. Все необходимые размеры l 0, l 1, l 2 и т. д. должны быть заданы в условиях задачи. В этом случае под знаком функции в уравнениях (5 14)—(5 17) должны быть величины Очевидно, внесение в этом случае под знак функции величин L 1, L 2, . . . Ln является необходимым. Во всех случаях список безразмерных величии должен соответствовать математической формулировке задачи. Произвольное же исключение или введение под знак функции новых переменных безусловно недопустимо. Любая подобного рода операция должна быть обоснована.

Очевидно, при неизменной математической формулировке задачи новые безразмерные величины могут быть получены соответствующим комбинированием старых безразмерных величии, однако при этом число переменных под знаком функции не должно измениться. (5. 19) Число Ре, полученное приведении к безразмерному виду уравнения энергии, можно представить как произведение двух безразмерных переменных: Безразмерная величина Pr = /a представляет собой новую переменною, называемую числом Прандтля. Число Прандтля целиком составлено из физических параметров, и поэтому и само является физическим параметром. Его можно записать и в виде (5. 20)

Числу Прандтля можно придать определенный физический смысл. Уравнение энергии и уравнение движения по записи аналогичны. При a = расчетные поля температур и скоростей будут подобны, если только аналогичны и условия однозначности. Условию a = соответствует равенство Рr = 1. Таким образом, при определенных, условиях числу Прандтля может быть придан смысл меры подобия полей температур и скоростей.
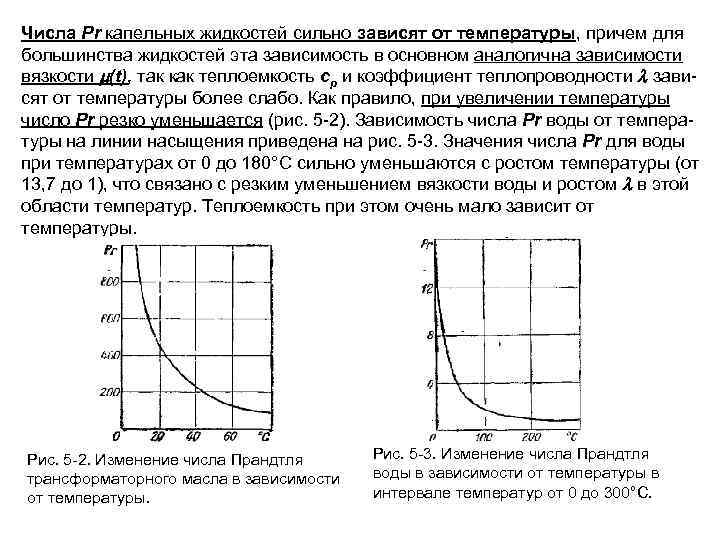
Числа Рr капельных жидкостей сильно зависят от температуры, причем для большинства жидкостей эта зависимость в основном аналогична зависимости вязкости (t), так как теплоемкость ср и коэффициент теплопроводности зави сят от температуры более слабо. Как правило, при увеличении температуры число Рr резко уменьшается (рис. 5 2). Зависимость числа Рr воды от темпера туры на линии насыщения приведена на рис. 5 3. Значения числа Рr для воды при температурах от 0 до 180°С сильно уменьшаются с ростом температуры (от 13, 7 до 1), что связано с резким уменьшением вязкости воды и ростом в этой области температур. Теплоемкость при этом очень мало зависит от температуры. Рис. 5 2. Изменение числа Прандтля трансформаторного масла в зависимости от температуры. Рис. 5 3. Изменение числа Прандтля воды в зависимости от температуры в интервале температур от 0 до 300°С.

При температурах от 130 до 310°С значения числа Рr для воды очень незначительна изменяются и близки к единице. Характер зависимости Рr от температуры, резко изменяется только при давлениях и температурах, близких к критическим. Число Рr газов практически не зависит ни от температуры, ни от давления и для данного газа является величиной постоянной, определяемой атомностью газа. В соответствии с кинетической теорией газов число Рr имеет следующие значения: Для одноатомных газов. . . . . 0, 67 Для двухатомных газов. . . . . 0, 72 Для трехатомных газов. . . 0, 8 Для четырехатомных и более газов. . . 1 Числа Рr тяжелых и щелочных жидких металлов, применяемых в качестве теплоносителей, изменяются в пределах Рr 0, 005 0, 05. Малые значения числа Рr жидких металлов объясняются высокой теплопроводностью последних.

В зависимости от значения числа Рr жидкости делят на три группы: жидкости с числами Рг << 1 (жидкие металлы), теплоносители с Рr 1 (неметаллические капельные жидкости при больших температурах и газы), жидкости с числами Рг>1 (неметаллические капельные жидкости). Учитывая, что Pe = Re Рr, уравнения подобия (5 14)—(5 17) можно записать в виде Nu = F 1(Xc, Yс, Re, Pr, Gr); (5. 21) =F 2(X, Y, Re, Pr, Gr); (5. 22) WX=F 3(X, Y, Re, Pr, Gr); (5. 23) Wv=F 4(X, Y, Re, Pr, Gr). (5. 24) Исходя из уравнений (5 14) — (5 17) и (5 21) — (5 24), безразмерные переменные можно разделить на два вида: Определяемые — это числа, в которые входят искомые зависимые переменные; в рассматриваемом случае зависимыми являются , , x и y следовательно, определяемыми являются Nu, , Wx и Wv; определяющие — это числа, целиком составленные из независимых переменных и постоянных величин, входящих в условия однозначности; в рассматриваемом случае определяющими являются X, Y, Re, Рr (или Ре) и Gr. Числа подобия, составленные из наперед заданных параметров (постоянных) математического описания процесса, называют также критериями подобия.

УСЛОВИЯ ПОДОБИЯ ФИЗИЧЕСКИХ ПРОЦЕССОВ Полученная система безразмерных дифференциальных уравнений (5 10) — (5 13), так же как и исходная система размерных уравнений, описывает бесконечное множество конкретных процессов конвективного теплообмена. Уравнения будут справедливы для любого процесса теплоотдачи между твердым телом и несжимаемой жидкостью, удовлетворяющего данной формулировке задачи. Таким образом, записанная ранее система дифферен циальных безразмерных уравнений описывает совокупность физических процессов, характеризующихся одинаковым механизмом. Дифференциальное уравнение теплопроводности 2 t = 0 описывает бесчисленное множество конкретных процессов, принадлежащих к одному и тому же классу. Общность этих процессов определяется одинаковым механизмом процесса распространения тепла. Однако известны и другие дифференциальные уравнения, аналогичные по форме записи уравнению теплопроводности, например уравнение электрического потенциала. Если для температуры и электрического потенциала ввести одинаковые обозначения, то оба уравнения по своему внешнему виду не будут отличаться друг от друга. Однако, хотя по форме записи оба уравнения совпадают, физическое содержание входящих в эти уравнения величин различно. Те явления природы, которые описываются одинаковыми по форме записи дифференциальными уравнениями, но различны по своему физическому содержанию, называются аналогичными.

Дифференциальные уравнения отражают наиболее общие черты явлении и не учитывают частные, количественные особенности. Такими особенностями являются форма и размеры системы, в которой протекает физический процесс; к частным особенностям относятся также физические свойства рабочих тел, участвующих в процессе, условия протекания процесса на границах системы и др. Частные особенности различных явлений одного и того же класса определяются с помощью условий однозначности. Проведенный анализ системы безразмерных дифференциальных уравнений и условий однозначности делает более понятными общие условия подобия физических процессов, сформулированные ниже в виде трех правил: 1. Подобные процессы должны быть качественно одинаковыми, т. е. они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями. 2. Условия однозначности подобных процессов должны быть одинаковыми во всем, кроме числовых значений размерных постоянных, содержащихся в этих условиях. 3. Одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковое числовое значение.

Сформулированные условия являются определением подобия физических процессов. Первое условие говорит, что подобные процессы должны относиться к одному и тому же классу физических явлений. Помимо одинаковой физической природы подобные процессы должны характеризоваться одинаковыми по записи дифференциальными уравнениями. Во многих задачах конвективного теплообмена при вынужденном движении можно пренебречь силами тяжести. Очевидно, равенство сил тяжести нулю меняет механизм и математическую запись рассматриваемого процесса. При рассмотрении свободного движения в большом объеме можно пренебречь градиентом давления в жидкости. Исключение градиента давления из уравнения движения приводит к иной записи уравнения, меняется класс рассматриваемого явления. Таким образом, подобные процессы должны быть процессами конвективного теплообмена, характеризующимися одинаковой природой, одинаковыми действующими силами. Отдельные разновидности процессов конвективного теплообмена могут описываться различными дифференциальными уравнениями (хотя бы они и были частными случаями более общих уравнений), и в этом случае они будут принадлежать к различным классам явлений. Изменение исходных дифференциальных уравнений в общем случае приводит к изменению системы безразмерных переменных, существенных для изучаемого процесса.

Второе условие подобия требует, чтобы условия однозначности подобных процессов были одинаковыми во всем, кроме числовых значений постоянных, содержащихся в этих условиях. В частном случае равенства числовых значений размерных постоянных, содержащихся в условиях однозначности, имеем тождественные процессы (если выполняются прочие условия подобия). Таким образом, запись размерных условий однозначности подобных процессов в общем виде (буквенном) должна быть идентична. При этом конкретные значения скорости набегающего потока 0, температура стенки tc и т. д. могут иметь различные числовые значения. Из сравнения граничных условий (а) и (г) видно, что несмотря па различные значения 0, tс, t 0 и др. , безразмерные граничные условия будут одинаковыми для всех этих процессов. Из первого и второго условий подобия следует, что подобные процессы должны описываться одинаковыми (тождественными) безразмерными дифференциальными уравнениями и безразмерными граничными условиями.

В безразмерной форме математическая формулировка рассматриваемых подобных процессов одна и та же. Следовательно, рассматриваемые подобные процессы описываются единой формулой, например Nu = f 1(Xc, Yс, Re, Pr); или =f 2(X, Y, Re, Pr); функция f 1 будет одна и та же для всех подобных процессов. То же самое можно оказать и о функции f 2 и т. д. Если система безразмерных уравнений и граничных условий достаточно сложна, то при нахождении функций f 1 и f 2 могут встретиться значительные математические трудности. Однако можно утверждать, что эти функции существуют. При соблюдении первых двух условий подобия исследуемые процессы будут зависеть от одних и тех же безразмерных переменных. Этот вывод неизбежно вытекает из того, что подобные процессы описываются тождественными безразмерными уравнениями и граничными условиями.

Первых двух условий недостаточно для установления физического подобия. Нужно добавить условие, что одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковое числовое значение, т. е. X=idem, Y=idem, Re=idem, Pr =idem, Gr=idem и т. п. Так как подобные процессы характеризуются одинаковыми функциями f 1, f 2 и т. д. и численно равными определяющими переменными, то определяемые одноименные переменные подобных процессов также будут иметь одинаковые значения, т. е. Nu = idem, Wx=idem, Wv= idem и т. д. Предположим, что рассматривается система размерных дифференци альных уравнений совместно с размерными граничными условиями. Решение уравнений дало бы определенную формулу. Для примера можно взять решения задач теплопроводности, рассмотренные ранее. Подстановка конкретных числовых значений аргументов , δ и t в формулу q= ( /δ) t дала бы определенное числовое значение зависимой переменной q. Очевидно, при одних и тех же значениях , δ и t все процессы теплопроводности, описываемые этой формулой, будут тождественны — это будет один и тот же процесс.

Иное дело, когда формула представлена в безразмерных переменных. Неизменность каждой в отдельности из определяющих величин X, Y, Ре, Рr и Gr, например, в уравнении =f(X, У, Re, Pr, Gr) дает одно и то же значение безразмерной температуры =(t—to)/(tc—to), однако размерные значения температур жидкости и стенки могут быть различны. Одинаковым значениям будет соответствовать множество различных по своим размерным температурным параметрам физических процессов. Только в частном случае может иметь место тождество процессов. Три условия подобия составляют содержание теоремы Кирничева— Гухмана (1931 г. ).

Помимо выполнения первых двух условий подобия для подобия нужно еще, чтобы одноименные определяющие безразмерные переменные были численно равны. При этом для подобия процессов в целом достаточно, чтобы были численно равны одноименные определяющие переменные, составленные из постоянных величин, заданных в условиях однозначности. Например, подобие двух процессов теплообмена при течении жидкости в трубах будет иметь место, если будут выполнены первые два условия подобия и будут численно равны одноименные определяющие переменные, составленные только из заданных параметров математического описания процесса (постоянных). Процессы в целом будут подобны. В то же время локальные (точечные) значении искомых переменных необходимо рассматривать в точках, характеризующихся равенством одноименных безразмерных координат (В случае нестационарных процессов должно иметь место и равенство безразмерных времен, например равенство чисел Фурье).

Таким образом, критериями подобия по существу являются определяющие безразмерные переменные, составленные из постоянных величин, не являющихся функцией независимых переменных. Теорию подобия можно рассматривать как учение о характерных для каждого процесса обобщенных безразмерных переменных. Замена размерных переменных обобщенными является основной чертой теории подобия. Безразмерные переменные можно получить для любого физического явления. Для этого необходимо иметь полное математическое описание рассматриваемого процесса. Знание математического описания является необходимой предпосылкой теории подобия. Сформулированные ранее условия подобия можно использовать для установления аналогии двух физических разнородных процессов. Для этого в первом условии подобия необходимо потребовать только формальной тождественности дифференциальных уравнений. Таким образом, понятие подобия можно распространить на физически неоднородные (аналогичные) процессы.

СЛЕДСТВИЯ ИЗ УСЛОВИЙ ПОДОБИЯ Пусть имеются два подобных процесса конвективного теплообмена, например, при течении жидкости в каналах произвольного поперечного сечения. Обозначим один процесс буквой А, другой — буквой Б. Масштабами линейных размеров выберем какой либо размер каналов, например, их высоты h. А и h. Б. Тогда и Будем рассматривать процессы А и Б в точках, характеризующихся равенствами: (5. 25) Точки, удовлетворяющие этим равенствам, называются сходственными. Для сходственных точек справедливы следующие соотношения: здесь cl=h. A/h. Б

Если равенства (5 25) выполняются для двух подобных процессов, то, очевидно, для сходственных точек должны выполняться и равенства где o. А и o. Б —значения скорости, заданные условиями однозначности; это может быть, например, скорость на входе соответственно в каналы А и Б. Из последнего равенства следует, что т. е. в любых сходственных точках подобных процессов отношение скоростей есть величина постоянная. Аналогично можно написать:

Таким образом, если процессы А и Б подобны, то любая физическая величина в данной точке процесса А пропорциональна соответствующей величине в сходственной точке процесса В, т. е. (5. 26) Коэффициенты пропорциональности с называют константами подобия. Они безразмерны; в общем случае не равны единице, не зависят ни от координат, ни от времени и различны для всех величин, имеющих различный физический смысл. Если все константы подобия равны единице, то процессы являются тождественными. Предположим, что подобным процессам А и Б подобен также процесс В. Тогда можно записать: причем с и с' в общем случае не равны. Таким образом, подобные процессы можно рассматривать как один и тот же процесс, но взятый в различном масштабе, причем масштабы разноименных величин могут быть неодинаковыми. Выбор констант подобия не может быть произведен произвольно.

МЕТОД РАЗМЕРНОСТЕЙ Необходимой предпосылкой теории подобия является математическое описание изучаемого процесса в виде дифференциальных (или интегродифференциальных) уравнений и условий однозначности. Из математической формулировки задачи следует перечень существенных для рассматриваемого процесса физических величин. Если перечень установлен, то выявление чисел подобия может быть произведено методом анализа размерностей. Иногда список размерных величии устанавливают интуитивно, без строгой формулировки краевой задачи. В этом случае возможны ошибки. Можно различать два вида физических величин: первичные (основные) и вторичные (производные). Первичные величины характеризуют какое либо физическое явление непосредственно, без связи с другими величинами. Вторичными являются величины, которые выражаются через первичные согласно определениям или физическим законам. Так, например, если длина и время являются первичными величинами, т. е. если длину нельзя выразить через время (и наоборот), то скорость, представляющая собой по определению отношение длины ко времени, является вторичной, производной величиной.

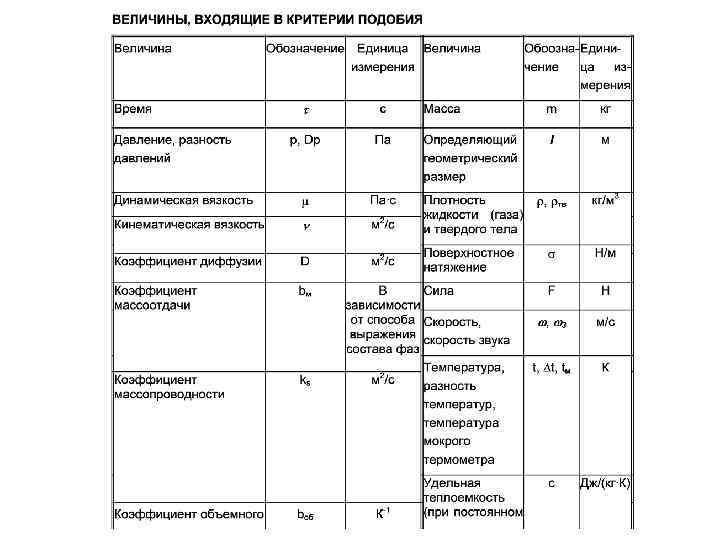
Выбор первичных величин, вообще говоря, произволен. В системе СИ за первичные выбраны длина (L), масса (M), время (Т), температура ( ) и т. д. При выборе первичных величин большое значение имеет вопрос об удобстве их применения. Символическое выражение производной величины через основные (первичные) называется размерностью. О размерности можно говорить только применительно к определенной системе первичных величин. Размерность можно представить в виде степенной формулы. Применительно к системе СИ формула размерности имеет вид: (5. 27) где [ ] — производная единила измерения; ni — действительные числа. Размерность вторичной величины относительно данной первичной i может быть охарактеризована значением показателя степени ni при этой первичной величине. Поэтому безразмерные числа часто называют величинами с нулевой размерностью, так как для них все показатели степени в формуле размерности (5 27) равны пулю. Согласно формуле (5 27) размерность первичной величины можно принять равной единице (берется относительно себя).

Помимо размерности физические величины характеризуются числовыми значениями. Числовые значения первичных величин получают путем прямого измерения, т. е. путем сопоставления измеряемой величины с некоторой величиной той же физической природы, выбранной в качестве стандарта и называемой единицей измерения. Числовое значение вторичной величины определяется косвенным путем, его находят по числовым значениям первичных величин. От выбора единиц измерения первичных величин зависят численные значения как первичных, так и вторичных величин. От выбора основных единиц измерения не зависят только численные значения безразмерных величин (величин с нулевой размерностью). Выбор перечня первичных величин и их единиц измерения является необходимым и основным шагом на пути создания системы единиц измерения.

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ КОНВЕКТИВНОГО ТЕПЛООБМЕНА При моделировании изучение процесса в образце заменяется исследованием этого же процесса на модели. Очевидно, процесс в модели должен быть осуществлен так, чтобы результаты его изучения можно было перенести на образец. Условия моделирования, т. е. условия, которым должна удовлетворять модель и протекающий в ней процесс, дает теория подобия. Если процесс в модели будет подобен процессу в образце, то результаты исследования на модели могут быть применены к образцу. Моделирование по существу включает в себя две самостоятель ные задачи. Во-первых, в модели необходимо осуществить процесс, подобный процессу, происходящему в образце, и, вовторых, выполнить на модели все требуемые измерения и наблюдения. Чтобы процессы в модели и образце были подобны, необходимо осуществить сформулированные ранее условия подобия.

Первое условие подобия говорит, что моделировать следует качественно одинаковые процессы, т. е. процессы, имеющие одинаковую физическую природу и описываемые одинаковыми дифференциальными уравнениями. Второе условие подобия требует, чтобы условия однозначности подобных процессов (в образце и модели) были одинаковы во всем, кроме числовых значений постоянных, содержащихся в этих условиях. Условия однозначности для стационарных процессов состоят: 1) из геометрических условий, характеризующих форму и размеры тела, в котором протекает процесс; 2) из физических условий, характеризующих физические свойства рассматриваемой среды; 3) из граничных условий, характеризующих особенности протекания процесса на границах жидкости.

Таким образом, необходимо осуществить геометрическое подобие образца и модели. Все размеры образца и модели, существенные для процесса конвективного теплообмена, должны быть связаны между собой соотношением lобр = ci lмод т. е. модель должна быть построена как точная копия образца, уменьшенная в ci раз. Конечно, копироваться должна не внешняя форма образца, а внутренняя конфигурация каналов, по которым движутся газы или жидкости. При осуществлении геометрического подобия следует только иметь в виду, что изменение геометрических размеров не должно привести к качественному изменению процесса в модели и, следовательно, к нарушению первого условия подобия. Если физические параметры постоянны, как это было принято ранее при выводе дифференциальных уравнений конвективного теплообмена, то выполнение подобия физических условий особых трудностей не представляет. Однородные физические параметры в модели и образце должны быть также связаны соответствующим масштабом преобразования с. При этом, если физические свойства жидкости в образце и модели одни и те же, с = 1.

При моделировании необходимо также осуществить подобие процессов на границах исследуемой жидкости. Чаще всего это условие ограничивается требованием подобия условий входа жидкости в образец и модель (чтобы обеспечить подобное распределение скоростей на входе) и требованием подобия температурных полей на входе в аппарате и на поверхности тел, участвующих в теплообмене. Подобия условий входа жидкости можно достичь путем устройства входного участка модели геометрически подобным входному участку образца. Если температура жидкости на входе в образец не меняется по сечению канала, условие подобия температурных полей на входе выдержать нетрудно. Для этого достаточно, чтобы в канале, подводящем жидкость или газ к модели, не было теплообмена.

Третье условие подобия требует, чтобы одноименные критерии подобных процессов имели одинаковые значения. При этом определяемые одноименные безразмерные переменные подобных процессов также будут иметь одинаковые значения. Конвективная теплоотдача существенно зависит от характера движения жидкости или газа. При вынужденном движении картина течения в первую очередь зависит от числа Рейнольдса. Поэтому при моделировании должно быть осуществлено равенство чисел Рейнольдса на входе в образец и модель: Для удовлетворении равенства критериев Рейнольдса скорость жидкости в модели надо увеличивать во столько раз, во сколько уменьшены геометрические размеры модели и наоборот. Очевидно, помимо равенства критериев Рейнольдса должно быть осуществлено и равенство других критериев подобия. В частности, должно выполняться условие Pr = idem.

Замена одной рабочей жидкости другой еще более усложняется ввиду переменности физических параметров. Чтобы учесть влияние переменности физических параметров, необходимо изменить систему дифференциальных уравнений конвективного теплообмена, полученную ранее. При выводе уравнений переменные значения физических параметров нельзя выносить из под знака производных. Кроме того, к основной системе дифференциальных уравнений нужно присоединить уравнения вида описывающие изменение физических параметров в зависимости от температуры (В некоторых задачах приходится учитывать и зависимость физических параметров от давления).

Согласно первому условию подобия эти уравнения, записанные в безразмерном виде, должны быть тождественными для одноименных параметров. Только в этом случае можно говорить о точном подобии. При этом физические параметры будут изменяться в рассматриваемом пространстве, т. е. будут зависеть от координат (при нестационарном процессе и от времени) и, следовательно, являться зависимыми переменными. Теория не даст какого либо общего единообразного уравнения, описывающего изменение данного физического параметра в зависимости от температуры и пригодного для всех жидкостей, используемых в настоящее время в технике. Такие уравнения имеются в лучшем случае для отдельных групп теплоносителей, рассматриваемых в определенном интервале изменения температур. Это обстоятельство накладывает серьезное ограничение на возможность точного моделирования, так как выполнить точное подобие процессов конвективного теплообмена в широком интервале изменения рода жидкости и температурных параметров процесса не представляется возможным. В частности, это приводит к тому, что при точном моделировании возможность замены газа капельной жидкостью практически исключается из за неподобия полей физических параметров в образце (газ) и модели (капельная жидкость).

Таким образом, выполнение точного подобия процессов конвективного теплообмена и, следовательно, проведение точного моделирования этих процессов часто наталкивается на непреодолимые трудности. В связи с этим возникает необходимость в разработке методов приближенного моделирования. Одной из возможностей приближенного моделирования является проявление так называемой автомодельности процесса относительно какого либо критерия. Говорят, что определяемая величина автомодельна относительно критерия подобия, если она не зависит от него. Если процесс автомоделей относительно какого либо критерия подобия, то при моделировании отпадает необходимость соблюдать равенство этого критерия для образца и модели. Явление автомодельности дает возможность упрощения дифференциальных уравнений и условий однозначности. Компоненты уравнений (или условий однозначности), учитывающие факторы, относительно которых процесс оказывается автомодельным, могут быть опущены или видоизменены.

Ввиду трудности точного моделирования на практике часто используется приближенный метод локального теплового моделирования. Особенность этого метода заключается в том, что подобие процессов стараются осуществить лишь в том месте, где производится исследование теплоотдачи. Например, если изучается теплоотдача при омывании жидкостью пучка труб, то в опытах в теплообмене может участвовать только одна из труб. Остальные трубы служат только для придания модели формы, подобной образцу. Данные о теплоотдаче получают из измерений, проведенных на единичной трубе. Предполагается, что теплоотдача испытуемой трубы в основном зависит от характера ее омывання, определяемого расположением системы труб, а не тепловыми условиями. Метод локального моделирования сравнительно прост и в ряде случаев позволяет получать достаточно точные результаты. Следует, однако, учитывать, что необоснованное применение метода локального теплового моделирования может привести и к значительным ошибкам.

Теплопередача-11(подобие).ppt