Подготовили Куркина Д Персидская К

Подготовили Куркина Д. Персидская К.

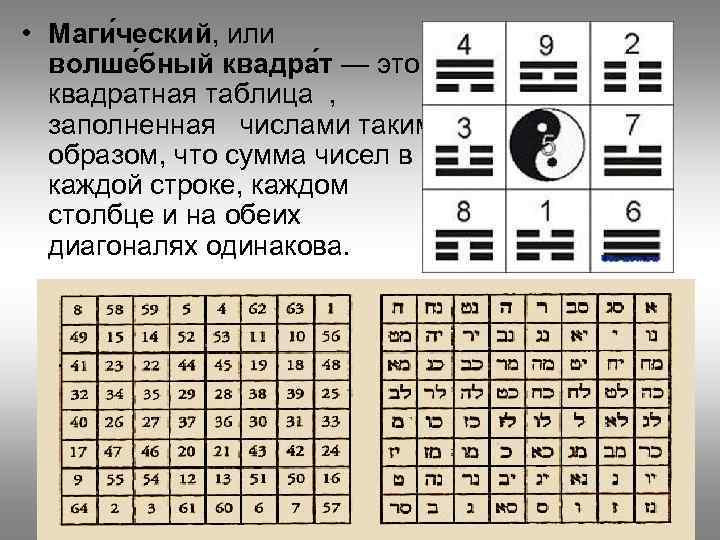• Маги ческий, или волше бный квадра т — это квадратная таблица , заполненная числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.

• Сумма чисел в каждой строке, столбце и на диагоналях называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n • Первые значения магических констант приведены в следующей таблице

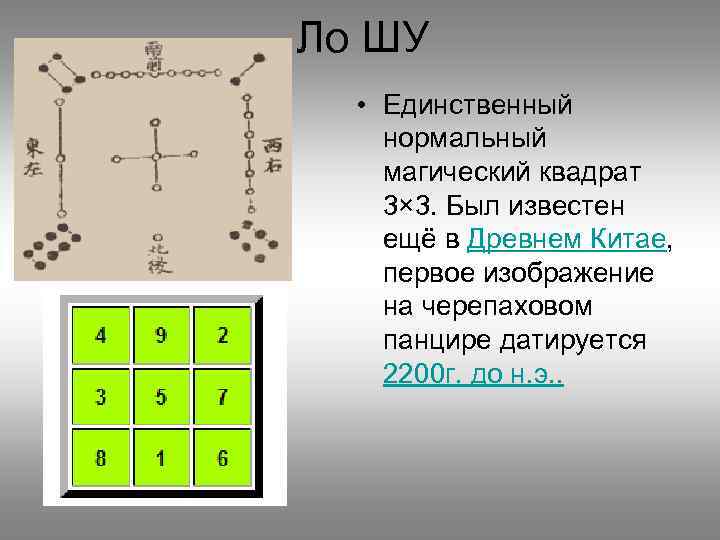Ло ШУ • Единственный нормальный магический квадрат 3× 3. Был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 г. до н. э. .

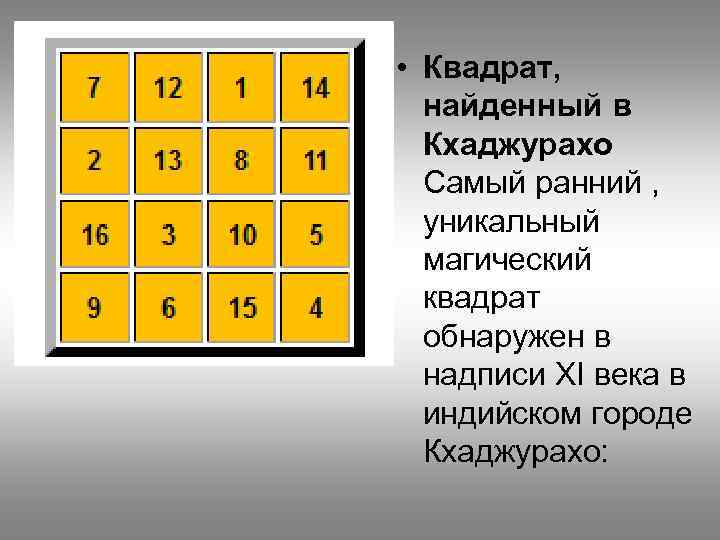• Квадрат, найденный в Кхаджурахо Самый ранний , уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо:

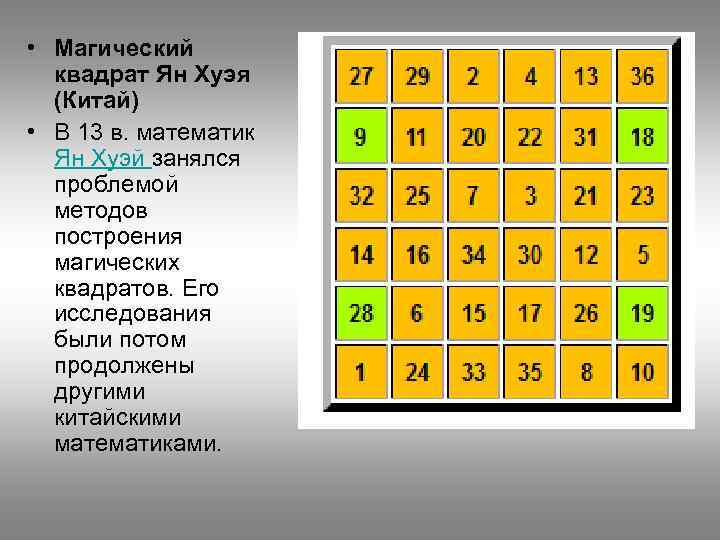• Магический квадрат Ян Хуэя (Китай) • В 13 в. математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками.

• Квадрат Альбрехта Дюрера • Магический квадрат 4× 4, изображённый на гравюре Альбрехта Дюрера «Меланхолия I» , считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания гравюры.

• Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл. • Если в квадратную матрицу n × n заносится не строго натуральный ряд чисел, то данный магический квадрат — нетрадиционный. Ниже представлены два таких магических квадрата, заполненные в основном простыми числами. Первый имеет порядок n=3 (квадрат Дьюдени); второй (размером 4 x 4) — квадрат Джонсона. Оба они были разработаны в начале двадцатого столетия

• Последний квадрат, построенный в 1913 г. Дж. Н. Манси, примечателен тем, что он составлен из 143 последовательных простых чисел за исключением двух моментов: привлечена единица, которая не является простым числом, и не использовано единственное чётное простое число 2.

Для заданного нечетного n начертим квадратную таблицу размером nxn. Пристроим к этой таблице со всех четырех сторон террасы (пирамидки). В результате получим ступенчатую симметричную фигуру.

• • Начиная с левой вершины ступенчатой фигуры, заполним ее диагональные ряды последовательными натуральными числами от 1 до . После этого для получения классической матрицы N-го порядка числа, находящиеся в террасах, поставим на те места таблицы размером Nx. N, в которых они оказались бы, если перемещать их вместе с террасами до того момента, пока основания террас не примкнут к противоположной стороне таблицы.