Lektsia_9.ppt
- Количество слайдов: 30

ПОДБОР ПАРАМЕТРОВ. ПОИСК ОПТИМАЛЬНЫХ РЕШЕНИЙ

Команда Подбор параметра меню Сервис позволяет определить неизвестное значение (параметр), которое будет давать желаемый результат. Технология использования команды следующая: • решить нужную задачу с каким-либо начальным значением параметра; • выбрать команду Подбор параметра меню Сервис; • в окне диалога Подбор параметра в поле Установить в ячейке задать абсолютную ссылку на ячейку, содержащую расчетную формулу, а в поле Значение — то значение, которое следует получить в качестве результата формулы; • в поле Изменяя значение ячейки ввести ссылку на ячейку с параметром; • нажать кнопку ОК или клавишу Enter, на экране появится окно диалога Результат подбора параметра; • для сохранения найденного значения нажать кнопку ОК. Для восстановления значения, которое было в ячейке с параметром до использования команды Подбор параметра нажать кнопку Отмена.

• При подборе параметра Excel использует итерационный процесс. Он проверяет для изменяемой ячейки одно значение за другим, пока не получит нужное решение. • Если задача подбора параметра занимает много времени, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы просмотреть результаты последовательных итераций. • По умолчанию команда Подбор параметра прекращает вычисления, когда выполняется 100 итераций, или при получении результата, который находится в пределах 0, 001 от заданного целевого значения. Если нужна большая точность, можно изменить используемые по умолчанию параметры на вкладке Вычисления команды Параметры меню Сервис. • Команда Подбор параметра находит только одно решение, даже если задача имеет несколько решений.
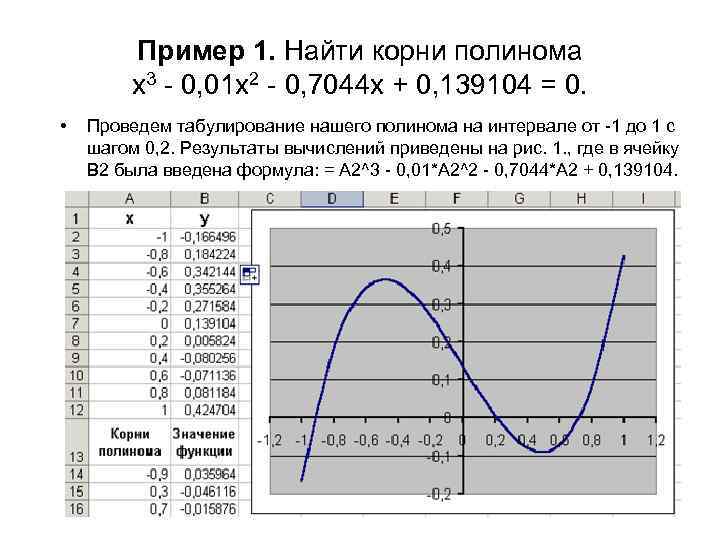
Пример 1. Найти корни полинома x 3 - 0, 01 x 2 - 0, 7044 x + 0, 139104 = 0. • Проведем табулирование нашего полинома на интервале от -1 до 1 с шагом 0, 2. Результаты вычислений приведены на рис. 1. , где в ячейку В 2 была введена формула: = A 2^3 - 0, 01*A 2^2 - 0, 7044*A 2 + 0, 139104.
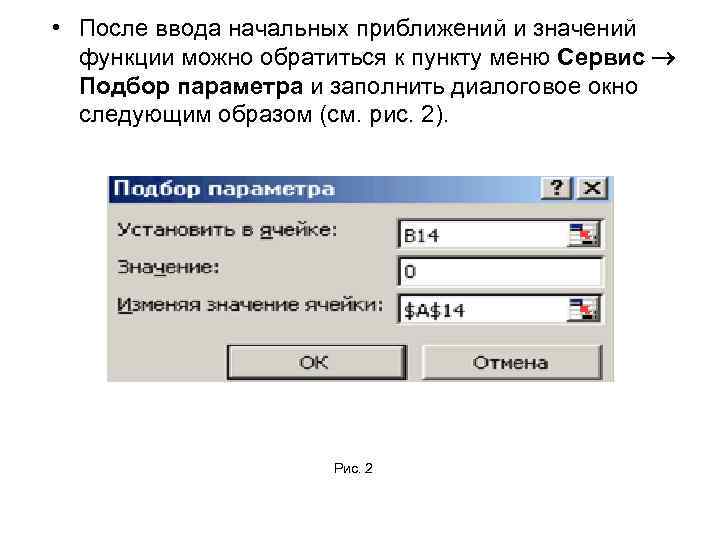
• После ввода начальных приближений и значений функции можно обратиться к пункту меню Сервис Подбор параметра и заполнить диалоговое окно следующим образом (см. рис. 2). Рис. 2
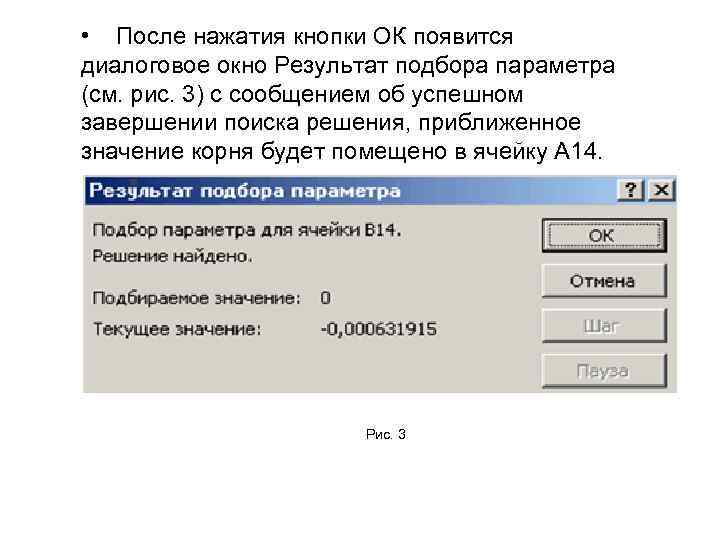
• После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра (см. рис. 3) с сообщением об успешном завершении поиска решения, приближенное значение корня будет помещено в ячейку А 14. Рис. 3

• Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А 15 и А 16 (см. рис. 4). Рис. 4

Пример 2. Решить уравнение ex - (2 x - 1)2 = 0. Проведем локализацию корней нелинейного уравнения. Для этого представим его в виде f(x) = g(x) , т. е. ex = (2 x - 1)2 или f(x) = ex, g(x) = (2 x - 1)2, и решим графически. Графическим решением уравнения f(x) = g(x) будет точка пересечения линий f(x) и g(x).
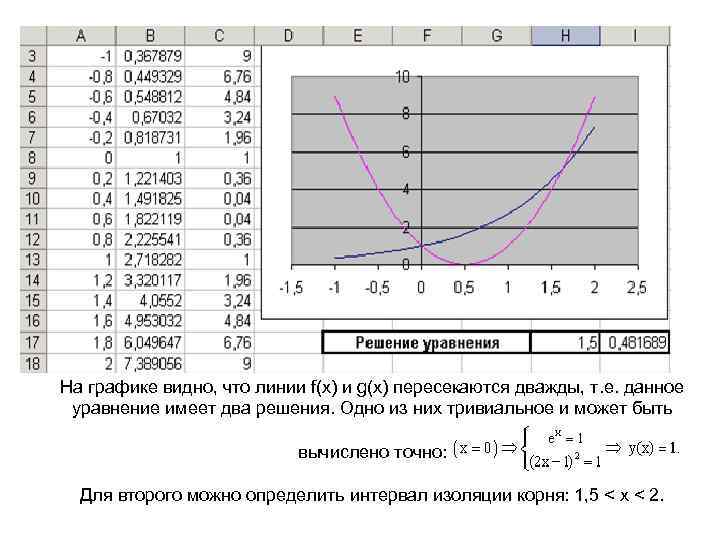
На графике видно, что линии f(x) и g(x) пересекаются дважды, т. е. данное уравнение имеет два решения. Одно из них тривиальное и может быть вычислено точно: Для второго можно определить интервал изоляции корня: 1, 5 < x < 2.
![• Теперь можно найти корень уравнения на отрезке [1. 5, 2] методом последовательных • Теперь можно найти корень уравнения на отрезке [1. 5, 2] методом последовательных](https://present5.com/presentation/3/-127729332_438823513.pdf-img/-127729332_438823513.pdf-10.jpg)
• Теперь можно найти корень уравнения на отрезке [1. 5, 2] методом последовательных приближений. • Введём начальное приближение в ячейку Н 17 = 1, 5, и само уравнение, со ссылкой на начальное приближение, в ячейку I 17 =EXP(H 17)-(2*H 17 -1)^2 (см. рис. 5).

Далее воспользуемся пунктом меню Сервис Подбор параметра и заполним диалоговое окно Подбор параметра (см. рис. 6). Рис. 6 Результат поиска решения будет выведен в ячейку Н 17 (см. рис. 7). Рис. 7

Поиск решений • Поиск решений может применяться для решения задач, которые включают много изменяемых ячеек, и помогает найти комбинацию переменных, которые максимизируют или минимизируют значение в целевой ячейке. • Он также позволяет задать одно или несколько ограничений условий, которые должны выполняться при поиске решений. • Для запуска этого инструмента следует выполнить команду Поиск решения меню Сервис.

• В диалоговом окне Поиск решения в поле Установить целевую ячейку задается цель, которую должен достичь поиск решения. • Целевая ячейка может быть задана ссылкой или именем. Поиск решения может находить конкретное значение целевой функции. • В этом случае, задав только изменяемую ячейку без указания ограничений, можно использовать Поиск решения вместо команды Подбор параметра.

• Цель поиска решений может не задаваться. Тогда поле Установить целевую ячейку следует оставить пустым, нажать кнопку Параметры и установить флажок Показывать результаты итераций. • Поиск решения будет перебирать комбинации изменяемых ячеек, которые удовлетворяют заданным ограничениям. • Пользователь может выбрать нужное решение, но оно необязательно будет оптимальным.

• В поле Изменяя ячейки следует задать ячейки с переменными. Можно указать ссылки на ячейки или их имена. • Если ячейки находятся в несмежных диапазонах, их следует разделять точкой с запятой. • Вместо ввода ячеек можно нажать кнопку Предположить, и поиск решения сам предложит изменяемые ячейки, исходя из заданной целевой функции. Поле Изменяя ячейки нельзя оставить пустым, и указанные в нем ячейки обязательно должны влиять на значение целевой ячейки.

• Последний шаг определения поиска решений — задание ограничений. Он не является обязательным. Чтобы задать ограничения, следует в окне Поиск решения нажать кнопку Добавить и заполнить окно диалога Добавление ограничений. • Ограничение состоит из трех компонентов: 1. ссылки на ячейку, 2. оператора сравнения 3. значения ограничения. • В левой части от оператора сравнения кроме ссылки на ячейку может также задаваться ссылка на диапазон. В правой части может задаваться диапазон (той же размерности, что и в левой части), ссылка на ячейку или константное значение.

Пример 3. Решить систему уравнений: Рассмотрим, как можно решить систему уравнений: F 1(x)=0, F 2(x)=0, … Fn(x)=0 Для решения этой задачи ее можно сформулировать одним из следующих способов: 1. Найти минимум (максимум) функции при системе ограничений, заданной в виде равенств Fi(x) = 0; 2. Найти минимум функции В этом случае задача решается без ограничений.
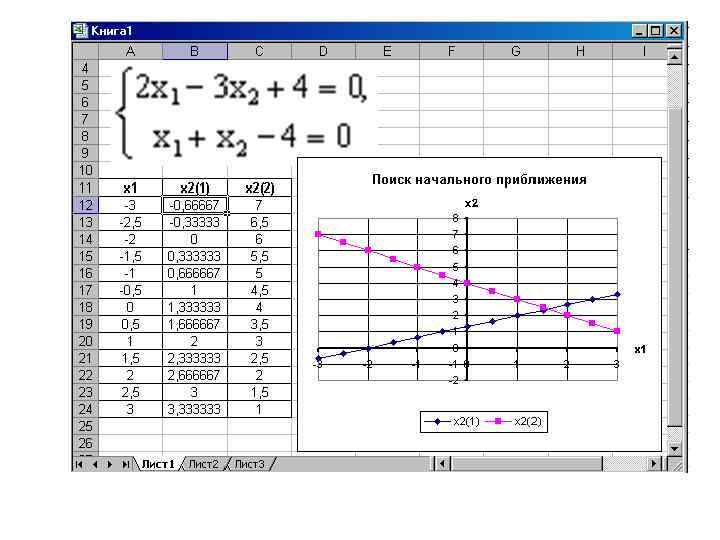
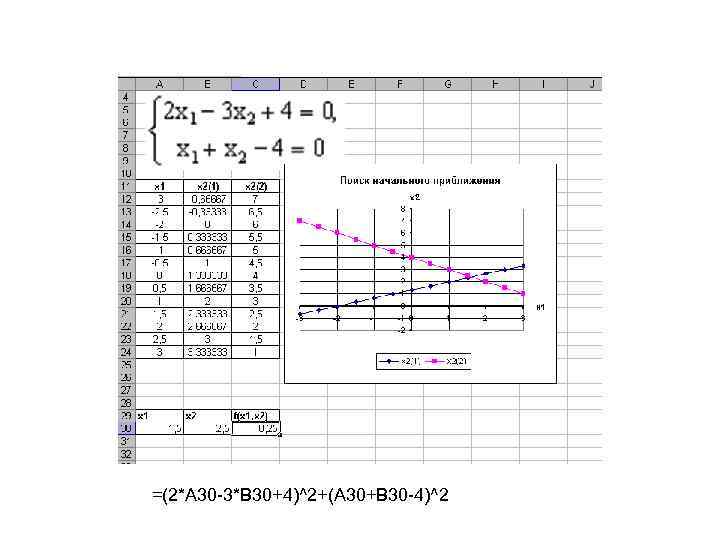
=(2*A 30 -3*B 30+4)^2+(A 30+B 30 -4)^2
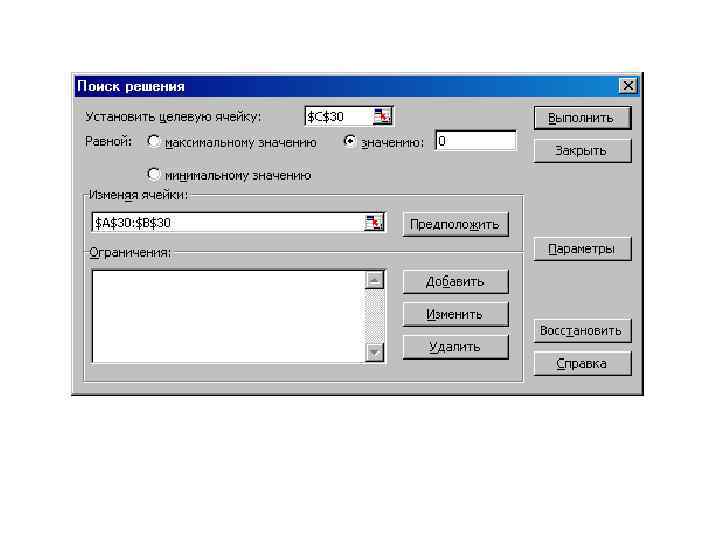

1 -й способ. • В ячейки А 1 и А 2 вводим числа 0 (здесь мы будем хранить x 1 и x 2). • В ячейки В 1 и В 2 вводим ограничения: В 1 = 2*А 1 -3*А 2, В 2 = А 1+А 2. • В ячейку С 1 введем функцию цели (эту ячейку мы будем минимизировать): С 1 = СУММ(B 1: B 2). Воспользуемся командой Сервис Поиск Решения и заполним появившееся диалоговое окно так, как показано на рис. 8. В результате решения поставленной задачи получим решение системы исходных уравнений: x 1 = 1, 6, Рис. 8 x 2 = 2, 4.
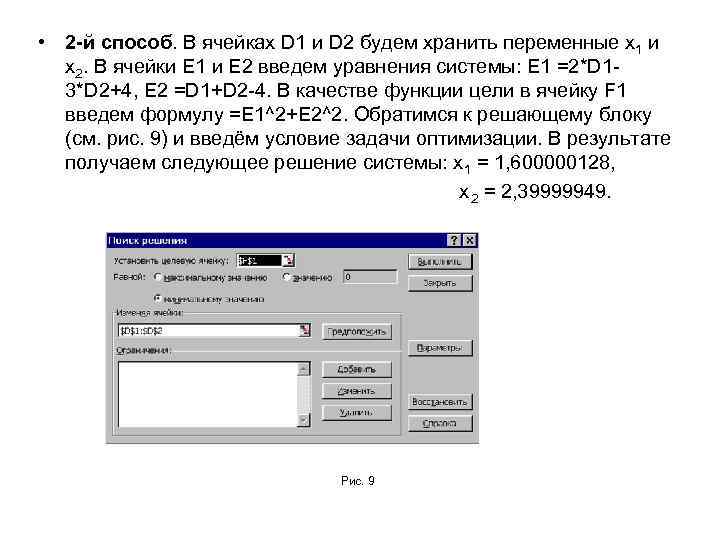
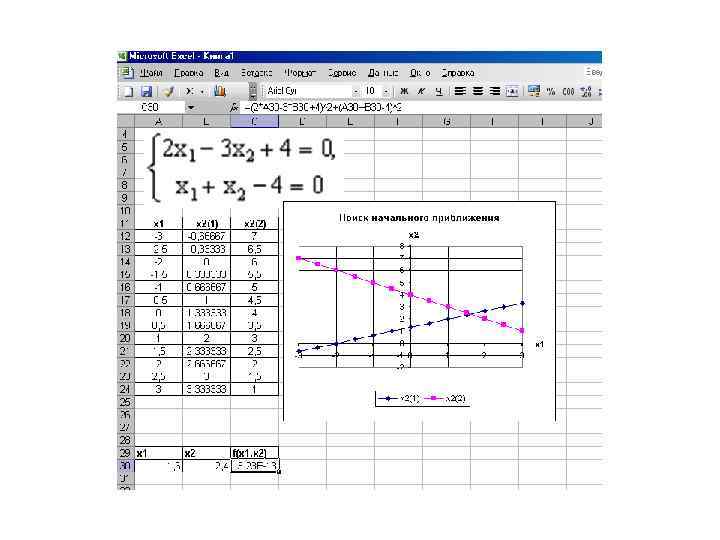
• 2 -й способ. В ячейках D 1 и D 2 будем хранить переменные x 1 и x 2. В ячейки E 1 и E 2 введем уравнения системы: E 1 =2*D 1 - 3*D 2+4, E 2 =D 1+D 2 -4. В качестве функции цели в ячейку F 1 введем формулу =E 1^2+E 2^2. Обратимся к решающему блоку (см. рис. 9) и введём условие задачи оптимизации. В результате получаем следующее решение системы: x 1 = 1, 600000128, x 2 = 2, 39999949. Рис. 9
![Если функция f(x) непрерывна на отрезке [a, b] и известна ее первообразная F(x), Если функция f(x) непрерывна на отрезке [a, b] и известна ее первообразная F(x),](https://present5.com/presentation/3/-127729332_438823513.pdf-img/-127729332_438823513.pdf-24.jpg)
Если функция f(x) непрерывна на отрезке [a, b] и известна ее первообразная F(x), то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона-Лейбница где

Формула трапеций Величина определенного интеграла численно равна площади криволинейной трапеции, ограниченной частью графика y=f(x), осью x и линиями x=a, x=b, т. е. S

Формула трапеций

Формула трапеций где

Формула трапеций Вычисление приближенного значения интеграла свелось к вычислению суммы значений подынтегральной функции. Абсолютной погрешностью называют разность точного и приближенного значений. формула для оценки погрешности в вычислении интеграла

Задание 1 вычислить приближенное значение интеграла с числом разбиений интервала интегрирования на 10 частей. Сравнить полученное значение интеграла с точным, определенным по формуле Ньютона-Лейбница (используя первообразную функцию).
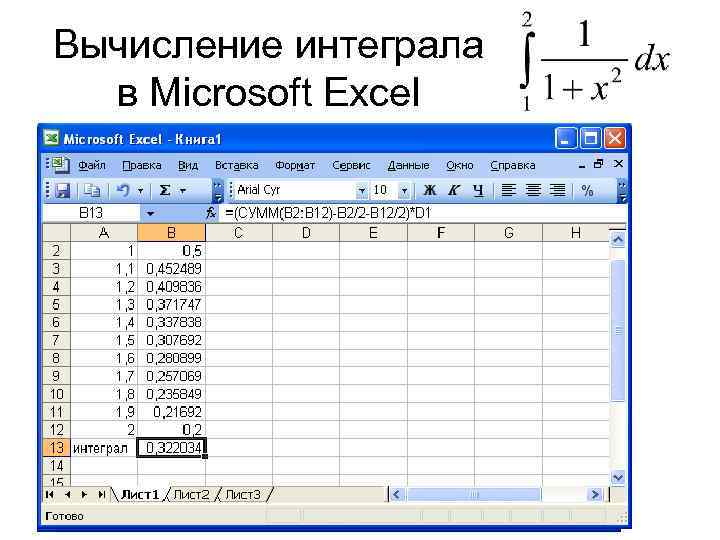
Вычисление интеграла в Microsoft Excel
Lektsia_9.ppt