Под устойчивостью понимается свойство системы возвращаться в прежнее

Под устойчивостью понимается свойство системы возвращаться в прежнее состояние равновесия после вывода ее из этого состояния и прекращения влияния задающего или возмущающего воздействия. Теорема Ляпунова устанавливает, что об устойчивости нелинейных систем при малых возмущениях можно судить по их линеаризованным уравнениям,

Условие устойчивости САУ Линеаризованное дифференциальное уравнение замкнутой системы Полное решение уравнения можно представить суммой вынужденной и переходной составляющих: Вынужденная составляющая, представляющая собой частное решение уравнения, является полезной составляющей управляемой величины. Она характеризует установившийся режим системы. Переходная составляющая является решением однородного дифференциального уравнения и имеет место в переходном режиме. Эта составляющая, по существу представляет ошибку системы в переходном режиме (отклонение системы от равновесного состояния)

Система будет устойчивой, если переходная составляющая в ней с течением времени затухает, т. е. Если при не стремится к нулю, а возрастает или представляет незатухающие колебания, то система неустойчива. Для определения устойчивости необходимо выявить только характер изменения переходной составляющей решения, т. е. достаточно исследовать однородное уравнение замкнутой системы Переходная составляющая (решение однородного уравнения) в случае не кратных корней может быть представлена в виде суммы: - начальное значение i-й компоненты переходной составляющей (постоянная интегрирования);

Чтобы система была устойчивой, решение должно удовлетворять требованию Устойчивость системы, зависит от значения корней характеристического уравнения замкнутой системы, Пусть среди них будет s корней вещественных и п- s комплексно сопряженных. Тогда решение можно записать в виде

Если все вещественные корни отрицательные , то каждая составляющая первой суммы в формуле представляет затухающую экспоненту и поэтому всех комплексных корней Если вещественные части отрицательны, то каждое слагаемое второй суммы представляет собой затухающее колебание и поэтому

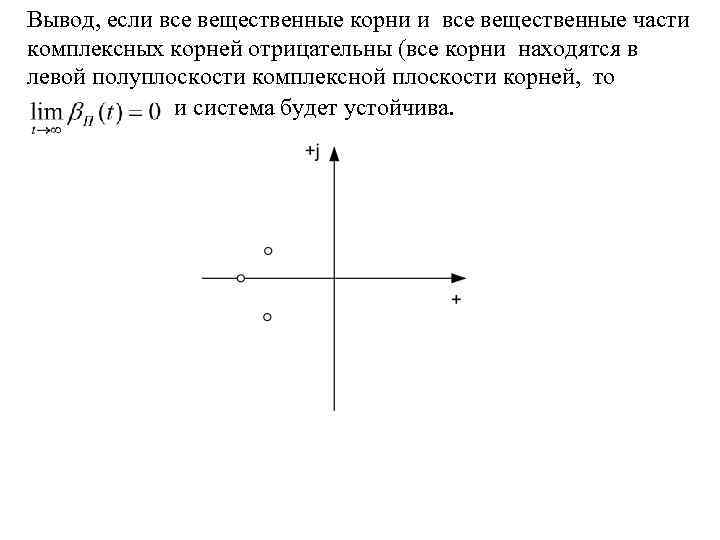Вывод, если все вещественные корни и все вещественные части комплексных корней отрицательны (все корни находятся в левой полуплоскости комплексной плоскости корней, то и система будет устойчива.

Если хотя бы один из вещественных корней или вещественная часть пары комплексных корней окажется положительной, то система будет неустойчивой, так как соответствующие этим и корням составляющие в решении с течением времени будут неограниченно возрастать.

Если вещественная часть хотя бы одного корня равна нулю, а вещественные части остальных корней отрицательны, то система находится на границе устойчивости. Условием устойчивости системы автоматического управления является отрицательность вещественных частей всех корней ее xaракmерuстического уравнения (расположение всех корней характеристического уравнения в левой полуплоскости комплексной плоскости корней).