Плотность m V единица измерения кг м 3 Поскольку

Плотность = m/V (единица измерения кг/м 3) Поскольку зачастую определение объема путем вычислений не обеспечивает достаточной точности, то плотность находят косвенным путем, заменяя измерение размеров взвешиванием. Пикнометрический метод Сначала взвешивают пикнометр с воздухом m 1, потом прибор заполняют до метки дистиллированной водой и снова взвешивают m 2. Воду выливают, высушивают пикнометр в сушильном шкафу. Затем в пикнометр помещают исследуемое вещество и снова взвешивают m 3. Добавляют в пикнометр воды до метки и определяют вес прибора с водой и телом m 4. Вычисления производят по формуле:

Задачи на пикнометрический метод При определении плотности твердого вещества пикнометрическим методом при комнатной температуре (25 ºС) были получены следующие результаты: m 1 = 22, 8799 г, m 2 = 47, 7876 г, m 3 = 53, 5705 г, m 4 = 65, 7072 г. Принять, что при этой температуре плотность дистиллированной воды равна 997 кг/м 3, воздуха – 1, 184 кг/м 3. Рассчитать из этих данных плотность исследуемого объекта. Для определения плотности используют пикнометр объемом 5 мл, масса которого составляет 20, 838 г. В него наливают некоторое количество дистиллированной воды и взвешивают. Масса прибора с водой составила 24, 397 г. Затем в него добавляют осмиевую пыль до тех пор, пока вода не дойдет до метки пикнометра. Суммарная масса составила 56, 727 г. Определить из этих данных плотность осмия (считая плотность воды равной 1 г/см 3).

Для сыпучих тел определяют т. н. насыпную плотность н – массу единицы объема рыхло насыпанного зернистого материала. Наиболее простым методом ее измерения является весовой. В нем сыпучий материал засыпают в воронку с цилиндрическим выпускным клапаном. Через него материал свободно пересыпается под действием силы тяжести в приемный сосуд точно определенного объема, пока он не переполнится. Избыток вещества удаляют пластиной и производят взвешивание.

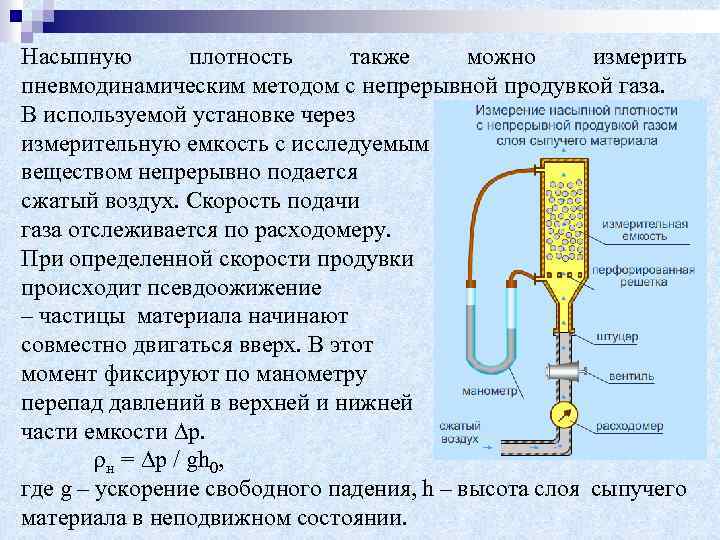Насыпную плотность также можно измерить пневмодинамическим методом с непрерывной продувкой газа. В используемой установке через измерительную емкость с исследуемым веществом непрерывно подается сжатый воздух. Скорость подачи газа отслеживается по расходомеру. При определенной скорости продувки происходит псевдоожижение – частицы материала начинают совместно двигаться вверх. В этот момент фиксируют по манометру перепад давлений в верхней и нижней части емкости р. н = р / gh 0, где g – ускорение свободного падения, h – высота слоя сыпучего материала в неподвижном состоянии.

С плотностью связано и такое понятие, как пористость – степень заполнения объема материала порами. П = (Vпор/Vест )∙ 100% где Vест – объем материала в естественном состоянии. П = (1 – ср / )∙ 100% где – истинная плотность материала. Наличие пор обуславливает способность материала поглощать воду – водопоглощение. Различают водопоглощение по массе и по объему. Вм = (mнас – mсух) / mсух ∙ 100% Во = (mнас – mсух) / (Vест вод) ∙ 100% Во = Вм ∙ ср / вод Масса образца горной породы, насыщенной водой, равна 42, 5 г, а в сухом состоянии – 40, 5 г. Определить среднюю плотность и пористость породы, если истинная плотность составляет 2, 96 г/см 3, а объемное водопоглощение – 10, 2%.

Масса образца каменного материала в сухом состоянии составляет 77 г, а после насыщения его водой – 79 г. Требуется определить среднюю плотность и пористость камня, если известно, что истинная плотность камня составляет 2, 67 г/см 3, а объемное водопоглощение – 4, 28 %. Высушенный образец горной породы в виде цилиндра высотой 5 см и диаметром 5 см имеет массу 245 г. После насыщения водой его масса стала 290 г. Определить среднюю плотность камня и водопоглощение по массе и объему. Плита из пенопласта на основе поливинилхлорида, средняя плотность которого составляет 115 кг/м 3, имеет размеры 600× 50 мм. За 24 часа материал поглощает 0, 25 кг воды на 1 м 2. Рассчитать водопоглощение по массе, а также пористость плиты, если истинная плотность материала 1, 4 г/см 3.

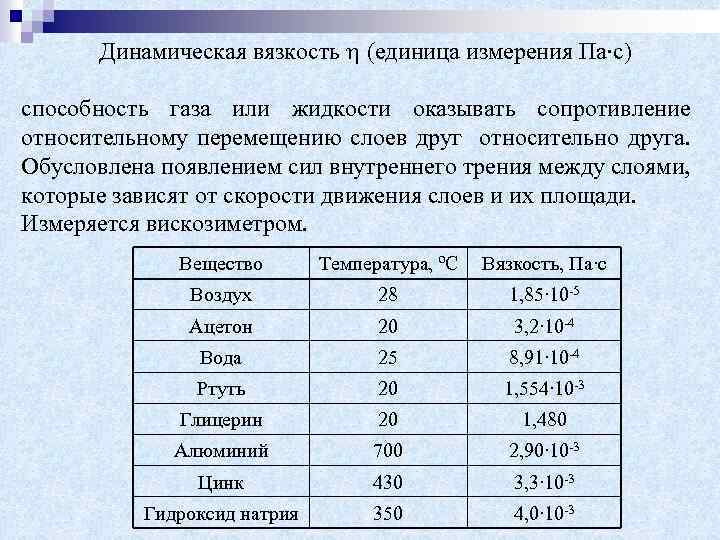Динамическая вязкость (единица измерения Па∙с) способность газа или жидкости оказывать сопротивление относительному перемещению слоев друг относительно друга. Обусловлена появлением сил внутреннего трения между слоями, которые зависят от скорости движения слоев и их площади. Измеряется вискозиметром. Вещество Температура, ºС Вязкость, Па∙с Воздух 28 1, 85∙ 10 -5 Ацетон 20 3, 2∙ 10 -4 Вода 25 8, 91∙ 10 -4 Ртуть 20 1, 554∙ 10 -3 Глицерин 20 1, 480 Алюминий 700 2, 90∙ 10 -3 Цинк 430 3, 3∙ 10 -3 Гидроксид натрия 350 4, 0∙ 10 -3

Для газа существует корреляция вязкости с плотностью: = (1/3) ∙ vср ∙ ∙ где v – средняя скорость теплового движения молекул, – длина свободного пробега. Для жидкости динамическую вязкость находят из закона Пуазейля, описывающего вытекание жидкости через отверстие. где p – давление, под которым жидкость поступает в отверстие, r – радиус капилляра, через который происходит истечение жидкости, l – длина капилляра, t – время истечения жидкости, V – объем жидкости.

Измерение вязкости в вискозиметре с падающим телом основано на законе Стокса, согласно которому скорость свободного падения металлического шарика в вязкой среде описывается уравнением: где v – скорость падения шарика, и ж – плотности шарика и жидкости, g – ускорение свободного падения, r – радиус шарика. Ротационный вискозиметр измеряет вращающий момент М, который необходимо приложить, чтобы ротор, помещенный в жидкость, сделал определенное число оборотов за единицу времени. Сравнивая эту величину со значением М 2, полученным в тех же условиях для жидкости с известной вязкостью 2, определяют 1 = 2 М 1/М 2.

Задачи на расчет вязкости Определите радиус капилляра вискозиметра объемом 30 мл, длиной 15 см, через который при температуре 20 ºС и давлении, равном 100 Па, ртуть вытекает за 22 с. Динамическая вязкость ртути равна 1, 554∙ 10 -3 Па∙с. Определите динамическую вязкость воды при 20 ºС, если время ее вытекания из вискозиметра объемом 20 мл с длиной капилляра 20 см и диаметром 4 мм при давлении 10 Па равно 64 с. Определите динамическую вязкость жидкости, если среднее время ее вытекания из вискозиметра составляет 5, 5 мин, тогда как для эталонной жидкости с вязкостью 6, 5∙ 10 -4 Па∙с измеренное в тех же условиях время вытекания составляет 400 с.

Коэффициент теплопроводности = Q·l / (S· Т·t) (единица измерения Вт/м∙К) Для газов коэффициент теплопроводности связан с плотностью: где vср – средняя скорость теплового движения частиц, l – длина свободного пробега, сv – удельная теплоемкость газа при постоянном объеме. Для твердых тел существует эмпирическая формула Некрасова: где ср – плотность материала в естественном состоянии (г/см 3).

Методики измерения коэффициента теплопроводности подразделяются на прямые и косвенные. Прямые методы связаны с определением теплового потока, проходящего через образец. К ним относится калориметрический метод. Образец помещают в установку и с одной стороны нагревают с определенной скоростью. Температура образца на разных его сторонах регистрируется термопарами, которые обеспечивают точность измерений до тысячных долей градуса. Количество сообщенной образцу теплоты определяется по закону Джоуля. Ленца: Q = I 2 Rt. Зная геометрические характеристики образца, рассчитывают по общей формуле.

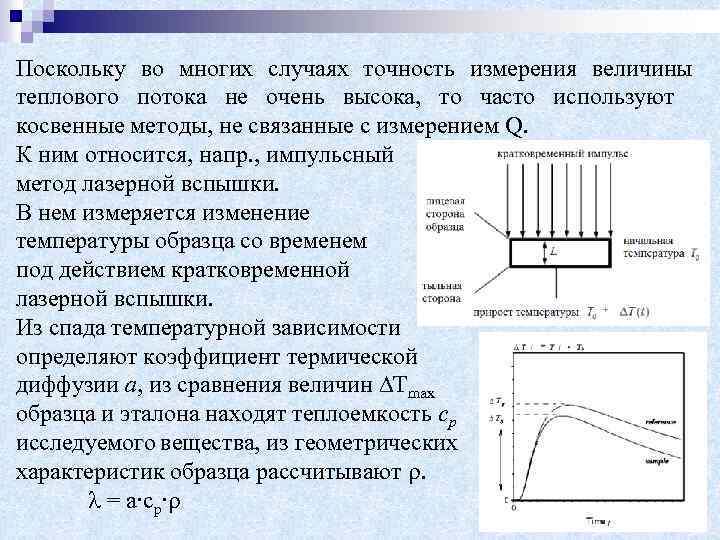Поскольку во многих случаях точность измерения величины теплового потока не очень высока, то часто используют косвенные методы, не связанные с измерением Q. К ним относится, напр. , импульсный метод лазерной вспышки. В нем измеряется изменение температуры образца со временем под действием кратковременной лазерной вспышки. Из спада температурной зависимости определяют коэффициент термической диффузии а, из сравнения величин Тmах образца и эталона находят теплоемкость ср исследуемого вещества, из геометрических характеристик образца рассчитывают . = а∙ср∙

Задачи на теплопроводность Какова теплопроводность материала, если при нагреве от 25 ºС до 100 ºС в течение 30 мин через образец в направлении, перпендикулярном к его поверхности, прошло 10, 5 к. Дж теплоты? Испытания проводились на образце цилиндрической формы диаметром 250 мм и высотой 50 мм. Наружная поверхность кирпичной стены толщиной 51 см имеет температуру -33 ºС, а внутренняя +22 ºС. Какое количество тепла проходит через 1 м 2 поверхности стены за 1 час? ( =2, 42 к. Дж/м·ч·К) Образец материала кубической формы с ребром 6 см имеет массу 391 г. Оценить теплопроводность данного материала.

Задачи на механические свойства твердых тел Механические свойства конструкционной стали определяли на цилиндрических образцах с начальным диаметром d 0 = 10 мм, площадью поперечного сечения S = 78, 5 мм 2 и длиной l 0 = 100 мм. Предельная нагрузка, пропорциональная величине относительного удлинения образца, Рпр = 34 к. Н. Нагрузка, при которой относительное остаточное удлинение составляет 0, 2% от первоначальной длины, равна Р 0, 2 = 41, 5 к. Н. Наибольшая нагрузка, предшествующая разрушению, составляет 68 к. Н. Длина рабочей части образца после разрыва l 1 = 110 мм. Диаметр шейки после разрыва d 1 = 8, 4 мм. Определить по этим данным: предел пропорциональности, условный предел текучести, временное сопротивление разрыву, относительные удлинение и сужение.

Какой диаметр должен иметь стальной стержень длиной 1, 3 м, если требуется удерживать груз массой 5, 8 т? Вычислить абсолютное удлинение стержня, приняв, что допустимое напряжение на растяжение равно 1170 кг/см, а модуль упругости 3, 8∙ 106 кг/см 2. Предел прочности на изгиб определяют по формуле: где Рразр – нагрузка разрушения, l – длина пролета, b – ширина и h – высота образца. Определить разрушающую нагрузку при испытании на изгиб бетонной балки квадратного сечения 10× 10 см и пролетом 120 см. Испытание проводится грузом, сосредоточенным в середине пролета. Возможный максимальный предел прочности при изгибе составляет 8 МПа.

В процессе испытания твердости стали по Бринеллю с помощью шарика диаметром 10 мм при нагрузке 30 к. Н был получен диаметр отпечатка d = 5, 05 мм. При испытании той же стали методом Роквелла по шкале В разность глубины погружения стального шарика под действием общей нагрузки (981 Н) и предварительной нагрузки (98 Н) равна 0, 108 мм. Рассчитать по этим данным твердость стали. Для испытания на ударную вязкость стали применяли стандартные квадратные образцы сечением 1× 1 см и длиной 5, 5 см с надрезом глубиной 0, 2 см. Запас энергии маятника до удара составил А 1 = 85 Дж. Неизрасходованная энергия маятника после излома образца стали составила А 2 = 15 Дж. Когда образец стали подвергли термообработке и провели аналогичное испытание, неизрасходованная энергия составила А 3 = 21 Дж. Определить ударную вязкость стали до и после термообработки, во сколько раз она изменилась?

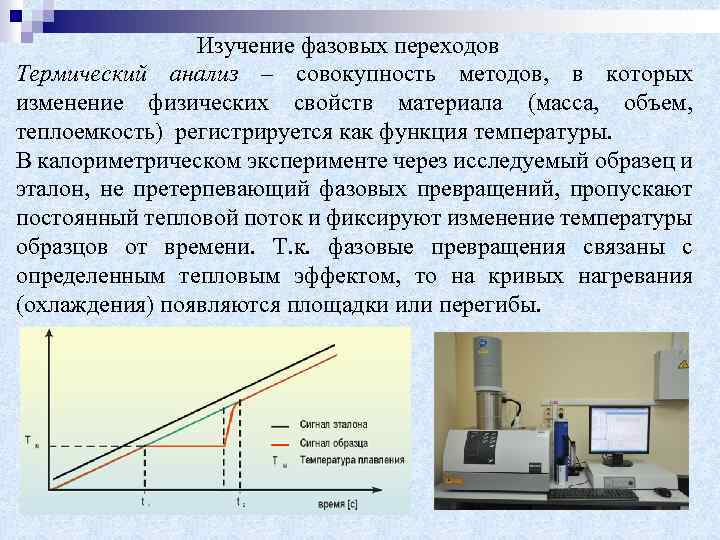Изучение фазовых переходов Термический анализ – совокупность методов, в которых изменение физических свойств материала (масса, объем, теплоемкость) регистрируется как функция температуры. В калориметрическом эксперименте через исследуемый образец и эталон, не претерпевающий фазовых превращений, пропускают постоянный тепловой поток и фиксируют изменение температуры образцов от времени. Т. к. фазовые превращения связаны с определенным тепловым эффектом, то на кривых нагревания (охлаждения) появляются площадки или перегибы.

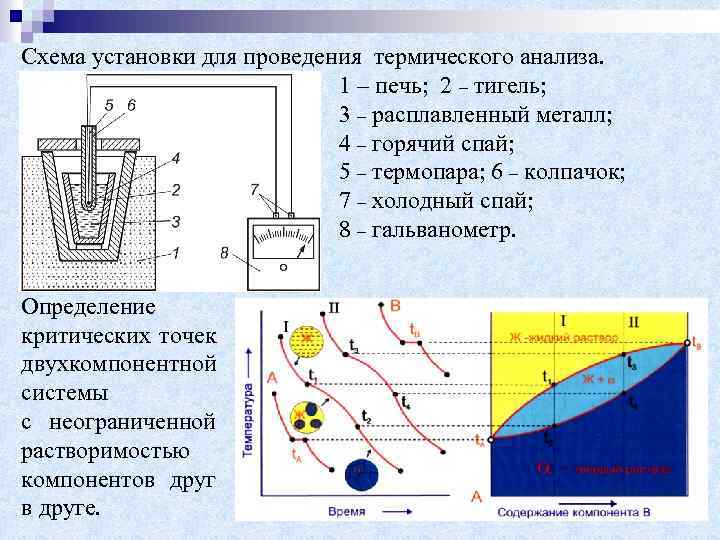Схема установки для проведения термического анализа. 1 – печь; 2 – тигель; 3 – расплавленный металл; 4 – горячий спай; 5 – термопара; 6 – колпачок; 7 – холодный спай; 8 – гальванометр. Определение критических точек двухкомпонентной системы с неограниченной растворимостью компонентов друге.

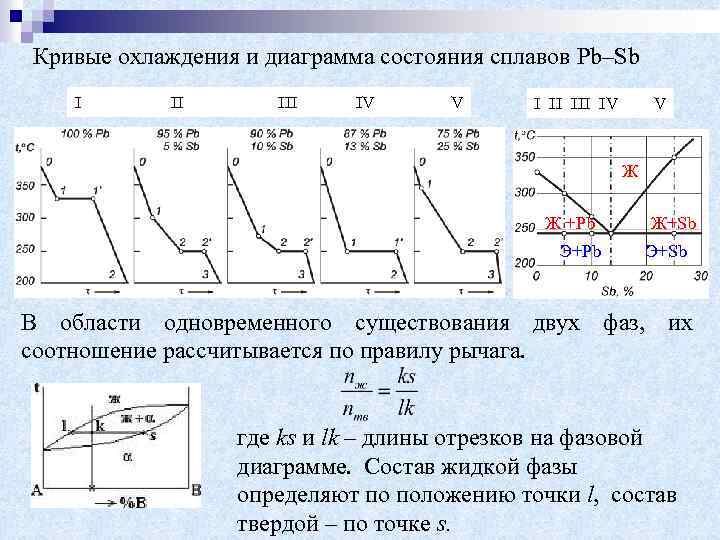Кривые охлаждения и диаграмма состояния сплавов Pb–Sb I II III IV V Ж Ж +Pb Э+Pb Ж+Sb Э+Sb В области одновременного существования двух фаз, их соотношение рассчитывается по правилу рычага. где ks и lk – длины отрезков на фазовой диаграмме. Состав жидкой фазы определяют по положению точки l, состав твердой – по точке s.

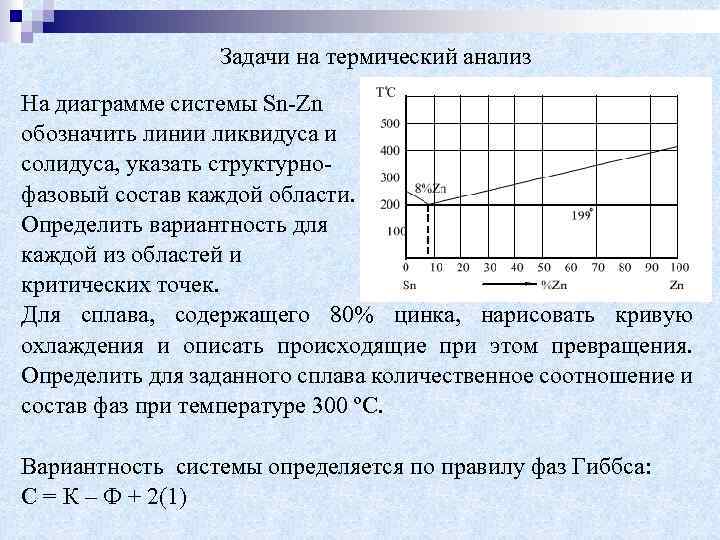Задачи на термический анализ На диаграмме системы Sn-Zn обозначить линии ликвидуса и солидуса, указать структурнофазовый состав каждой области. Определить вариантность для каждой из областей и критических точек. Для сплава, содержащего 80% цинка, нарисовать кривую охлаждения и описать происходящие при этом превращения. Определить для заданного сплава количественное соотношение и состав фаз при температуре 300 ºС. Вариантность системы определяется по правилу фаз Гиббса: С = К – Ф + 2(1)

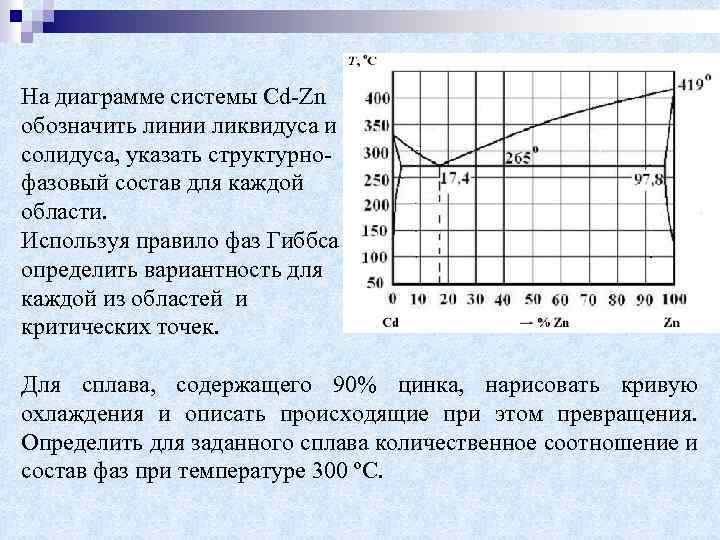На диаграмме системы Cd-Zn обозначить линии ликвидуса и солидуса, указать структурнофазовый состав для каждой области. Используя правило фаз Гиббса определить вариантность для каждой из областей и критических точек. Для сплава, содержащего 90% цинка, нарисовать кривую охлаждения и описать происходящие при этом превращения. Определить для заданного сплава количественное соотношение и состав фаз при температуре 300 ºС.