Плоскости 1 ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТЬ МНОЖЕСТВО

Плоскости 1

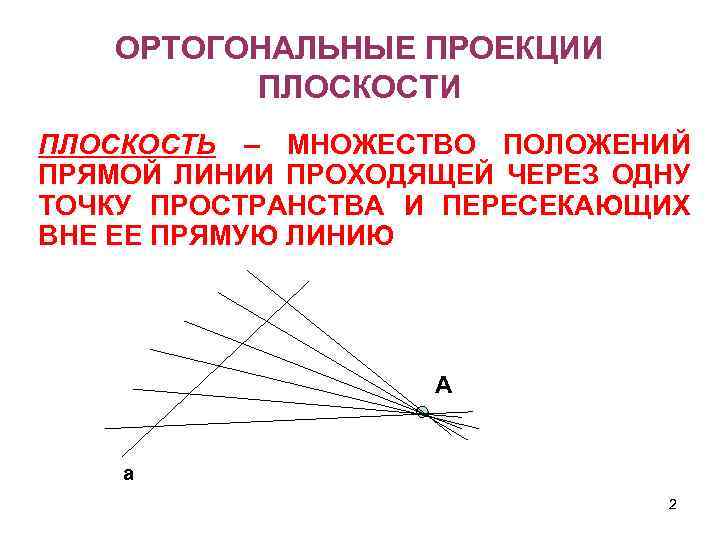
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ ЛИНИИ ПРОХОДЯЩЕЙ ЧЕРЕЗ ОДНУ ТОЧКУ ПРОСТРАНСТВА И ПЕРЕСЕКАЮЩИХ ВНЕ ЕЕ ПРЯМУЮ ЛИНИЮ A a 2

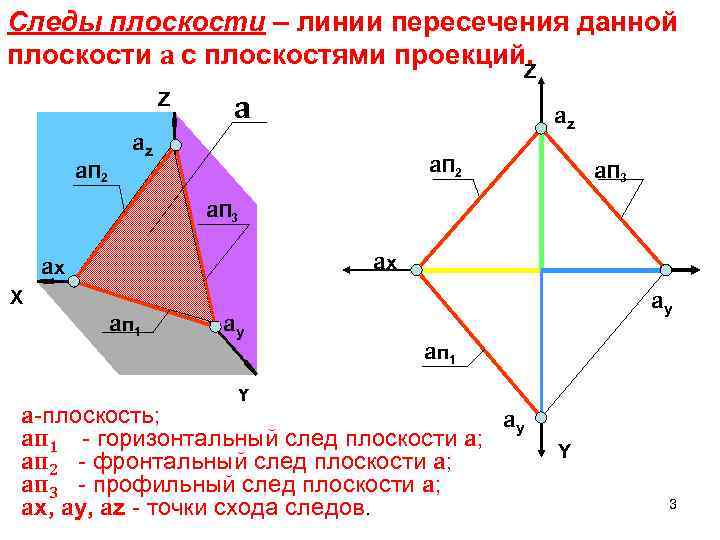
Следы плоскости – линии пересечения данной плоскости a с плоскостями проекций. Z Z a. П 2 a az az a. П 2 a. П 3 ax ax X a п 1 ay ay a п 1 Y a-плоскость; ay aп 1 - горизонтальный след плоскости a; aп 2 - фронтальный след плоскости a; aп 3 - профильный след плоскости a; ax, ay, az - точки схода следов. Y 3

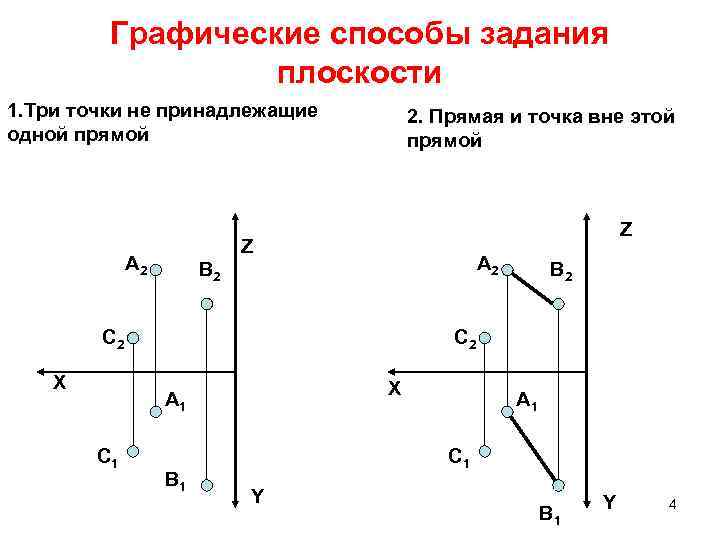
Графические способы задания плоскости 1. Три точки не принадлежащие одной прямой 2. Прямая и точка вне этой прямой Z Z А 2 В 2 C 2 X А 1 C 1 В 2 В 1 А 1 C 1 Y В 1 Y 4

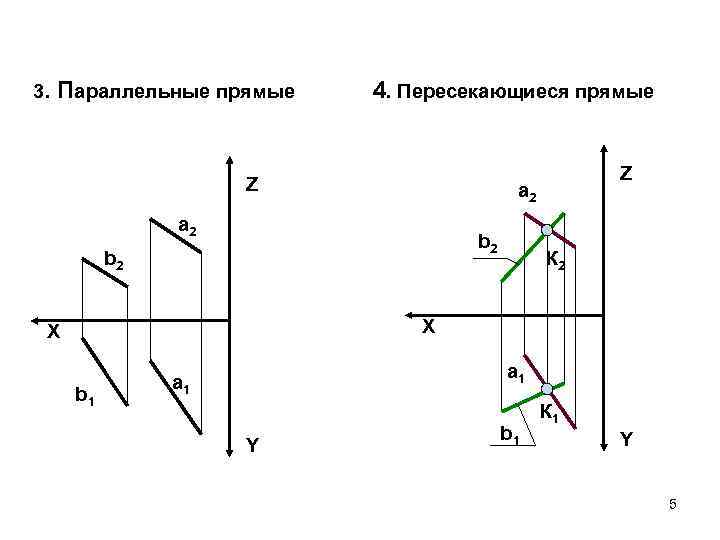
3. Параллельные прямые 4. Пересекающиеся прямые Z Z a 2 а 2 b 2 К 2 X X b 1 a 1 а 1 Y b 1 К 1 Y 5

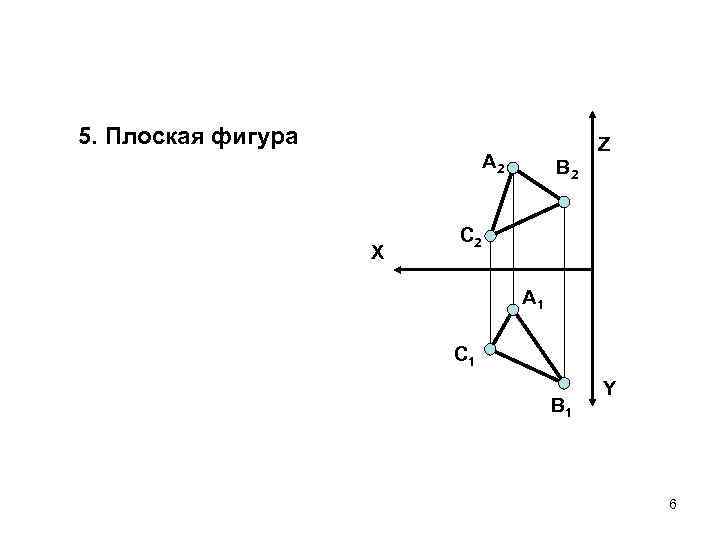5. Плоская фигура Z А 2 X В 2 C 2 А 1 C 1 В 1 Y 6

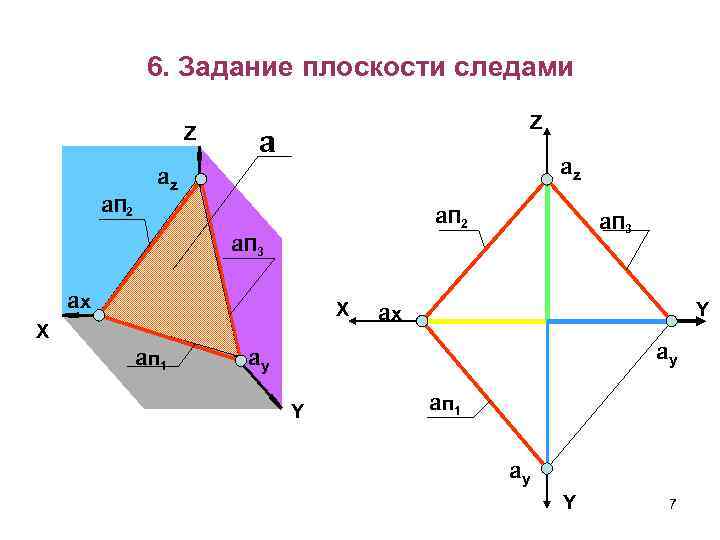6. Задание плоскости следами Z a. П 2 Z a az az a. П 2 a. П 3 ax X X a п 1 a. П 3 ax Y ay ay Y a п 1 ay Y 7

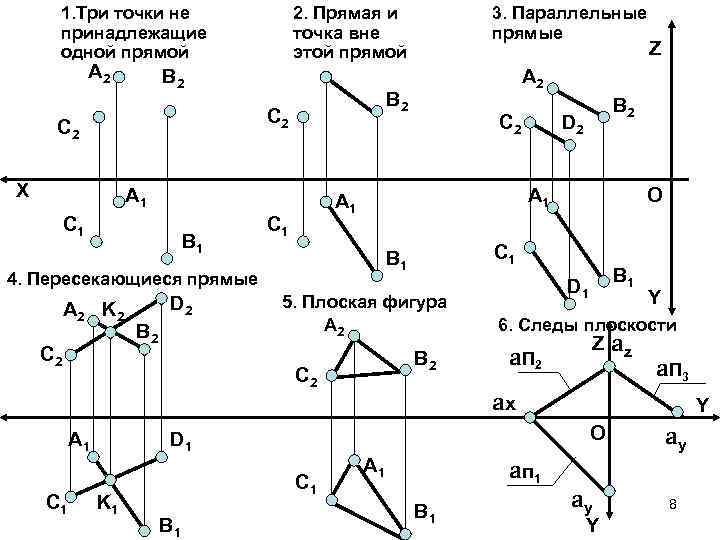1. Три точки не принадлежащие одной прямой А 2 2. Прямая и точка вне этой прямой В 2 X А 1 C 1 В 1 C 2 В 2 D 2 5. Плоская фигура А 2 В 2 Y 6. Следы плоскости a. П 2 Z az a. П 3 ax Y O C 1 В 1 D 1 K 1 O C 1 В 1 C 2 А 1 C 1 D 2 В 2 А 1 4. Пересекающиеся прямые А 2 K 2 C 2 А 1 C 1 Z А 2 В 2 C 2 3. Параллельные прямые А 1 a п 1 В 1 ay Y ay 8

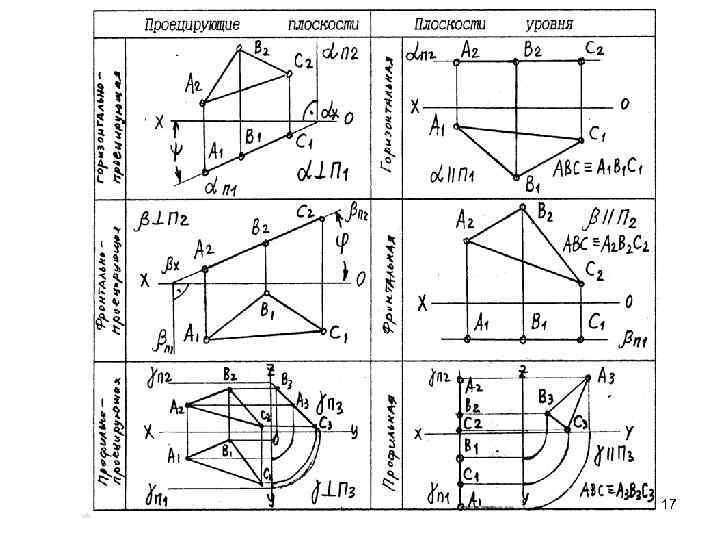
ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ Относительно плоскостей проекций плоскости разделяют на: плоскости общего положения; плоскости частного положения. Плоскости общего положения не параллельны и не перпендикулярны ни одной из плоскостей проекций. Плоскости частного положения разделяют на: плоскости параллельные плоскостям проекций – плоскости уровня; плоскости перпендикулярные плоскостям проекций – плоскости проецирующие. 9

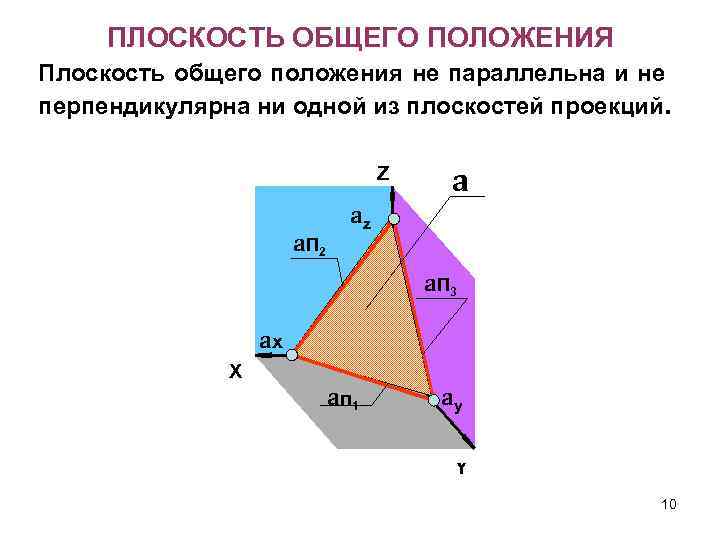ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций. Z a. П 2 a az a. П 3 ax X a п 1 ay Y 10

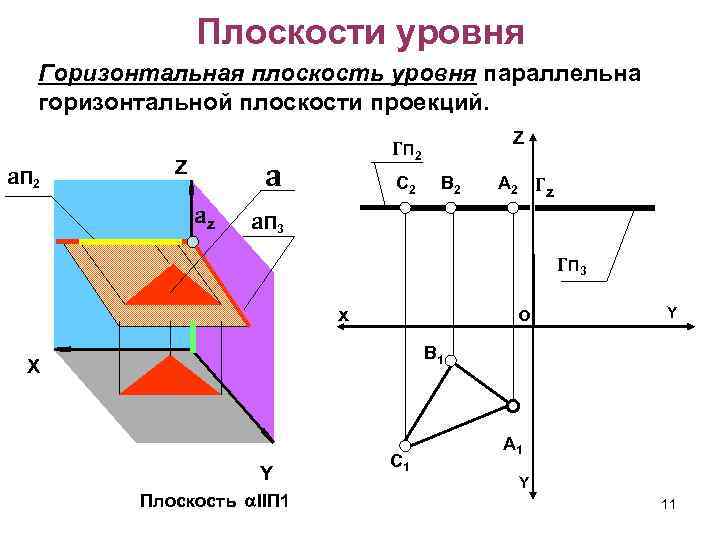Плоскости уровня Горизонтальная плоскость уровня параллельна горизонтальной плоскости проекций. a. П 2 a Z az Z ГП 2 С 2 В 2 А 2 Г z a. П 3 ГП 3 х о Y В 1 X Y Плоскость IIП 1 С 1 А 1 Y 11

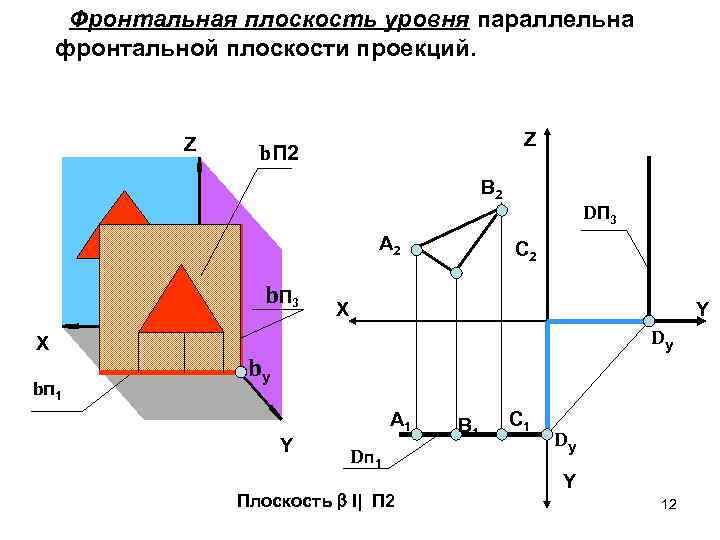Фронтальная плоскость уровня параллельна фронтальной плоскости проекций. Z Z b. П 2 В 2 А 2 b. П 3 X b п 1 DП 3 С 2 X Y Dy by Y А 1 D п 1 Плоскость I| П 2 В 1 С 1 Dy Y 12

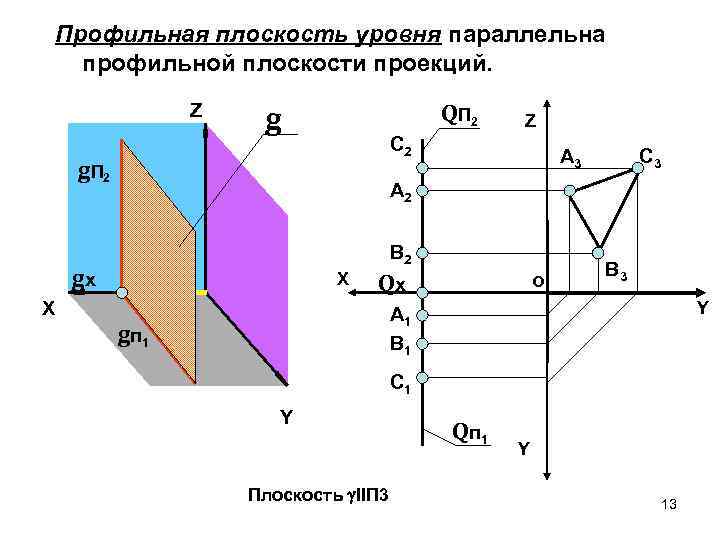Профильная плоскость уровня параллельна профильной плоскости проекций. Z QП 2 g Z С 2 g. П 2 А 3 С 3 А 2 В 2 gx X Qx X о В 3 Y А 1 В 1 g п 1 С 1 Y Плоскость IIП 3 Q п 1 Y 13

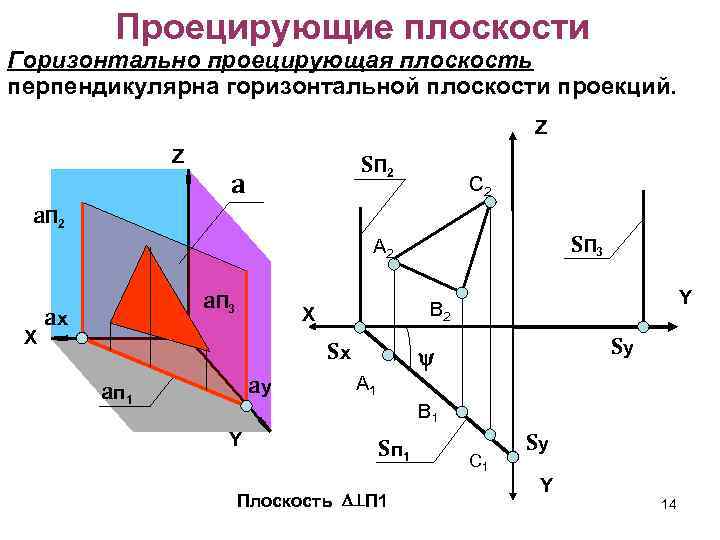Проецирующие плоскости Горизонтально проецирующая плоскость перпендикулярна горизонтальной плоскости проекций. Z Z SП 2 a С 2 a. П 2 SП 3 А 2 X a. П 3 ax X Sx ay a п 1 Y В 2 Sy А 1 В 1 Y S п 1 Плоскость D П 1 С 1 Sy Y 14

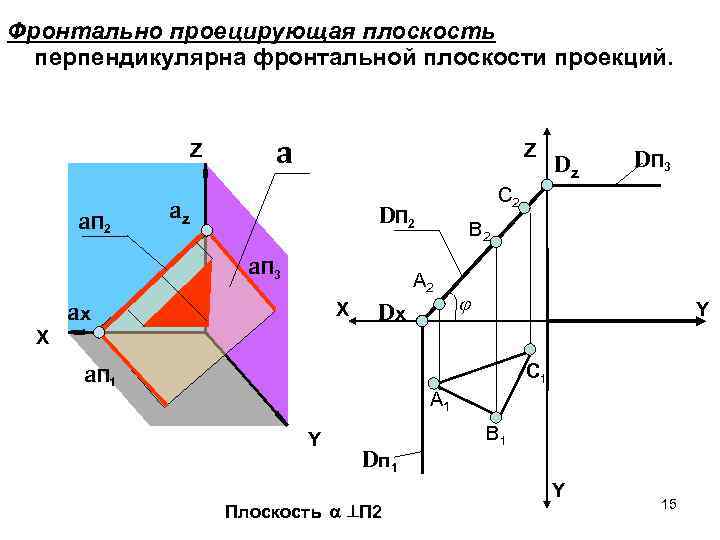Фронтально проецирующая плоскость перпендикулярна фронтальной плоскости проекций. Z a. П 2 a Z az В 2 А 2 ax X DП 3 С 2 DП 2 a. П 3 Dz Dx Y X a. П 1 С 1 А 1 Y D п 1 Плоскость П 2 В 1 Y 15

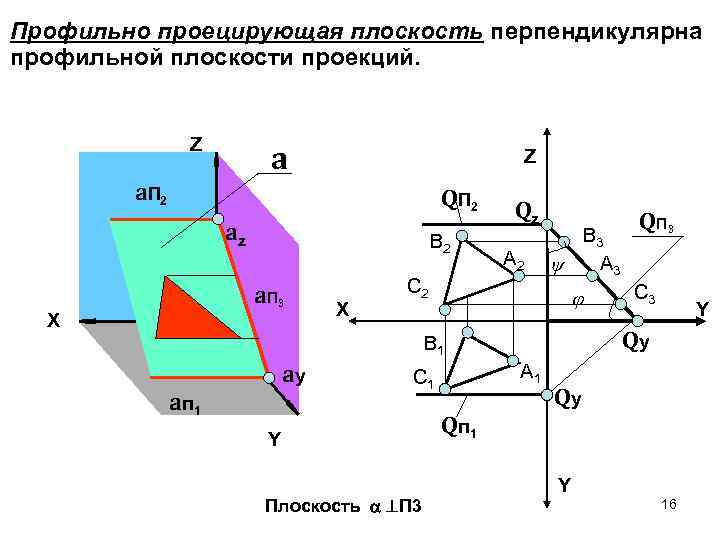Профильно проецирующая плоскость перпендикулярна профильной плоскости проекций. Z a. П 2 QП 2 az В 2 a. П 3 X X Qz А 2 С 2 В 3 А 3 a п 1 А 1 С 1 Y Плоскость П 3 С 3 Y Qy В 1 ay QП 3 Qy Q п 1 Y 16

17

ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ ПЛОСКОСТИ 1. Точка принадлежит плоскости, если она принадлежит прямой в этой плоскости; 2. Прямая принадлежит плоскости если она проходит: а) через две точки этой плоскости; б) через точку плоскости параллельно какой-либо прямой этой плоскости. 18

ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ 1. ЛИНИИ УРОВНЯ ПЛОСКОСТИ – линии параллельные плоскостям проекций и принадлежащие данной плоскости; 2. ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ – определяют угол наклона данной плоскости к одной из плоскостей проекций. ЛНН перпендикулярны линиям уровня: горизонтали на плоскости П 1; фронтали на П 2. 19

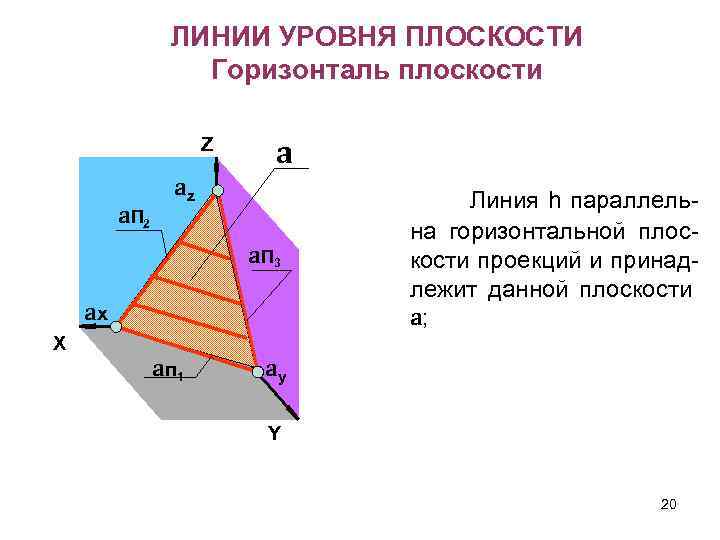ЛИНИИ УРОВНЯ ПЛОСКОСТИ Горизонталь плоскости Z a. П 2 a az a. П 3 ax X a п 1 Линия h параллельна горизонтальной плоскости проекций и принадлежит данной плоскости a; ay Y 20

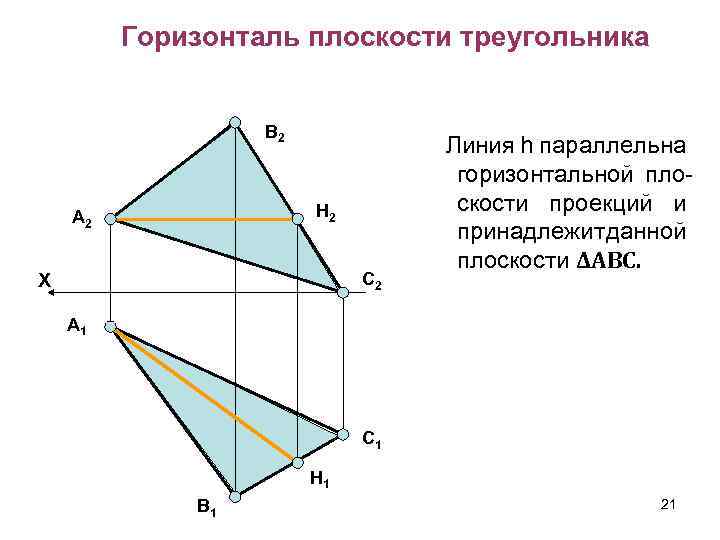Горизонталь плоскости треугольника В 2 H 2 А 2 С 2 X Линия h параллельна горизонтальной плоскости проекций и принадлежит данной плоскости ΔАВС. А 1 С 1 H 1 В 1 21

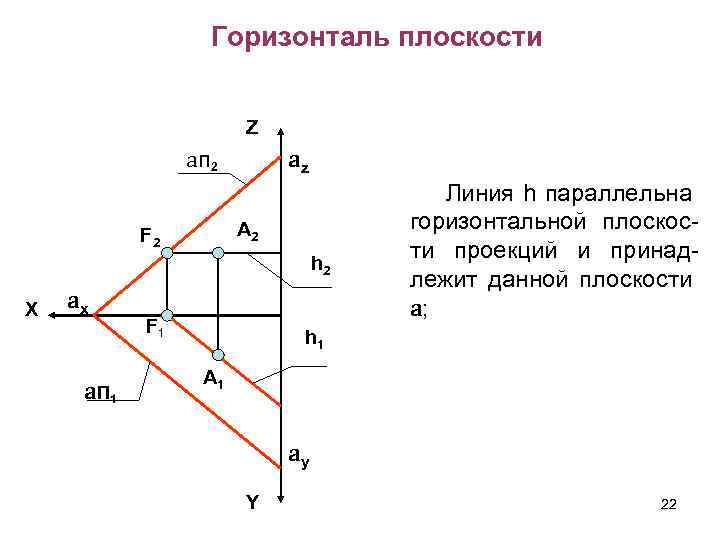Горизонталь плоскости Z aп 2 az А 2 F 2 h 2 X ax a. П 1 F 1 Линия h параллельна горизонтальной плоскости проекций и принадлежит данной плоскости a; h 1 А 1 ay Y 22

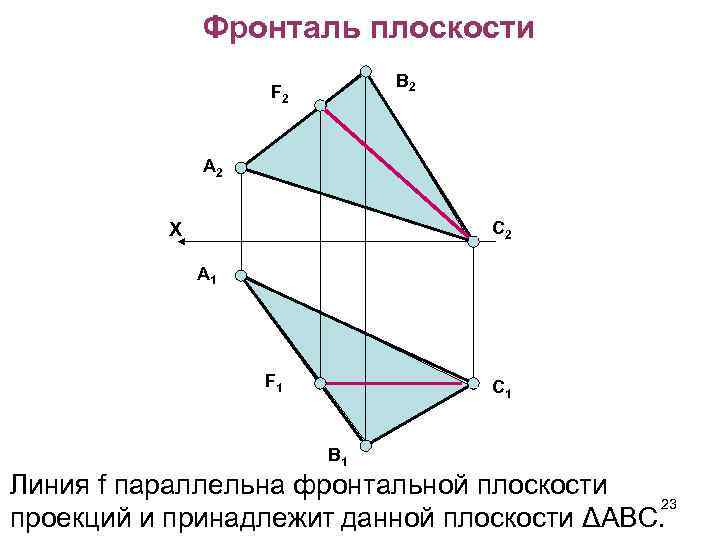Фронталь плоскости В 2 F 2 А 2 С 2 X А 1 F 1 С 1 В 1 Линия f параллельна фронтальной плоскости 23 проекций и принадлежит данной плоскости ΔАВС.

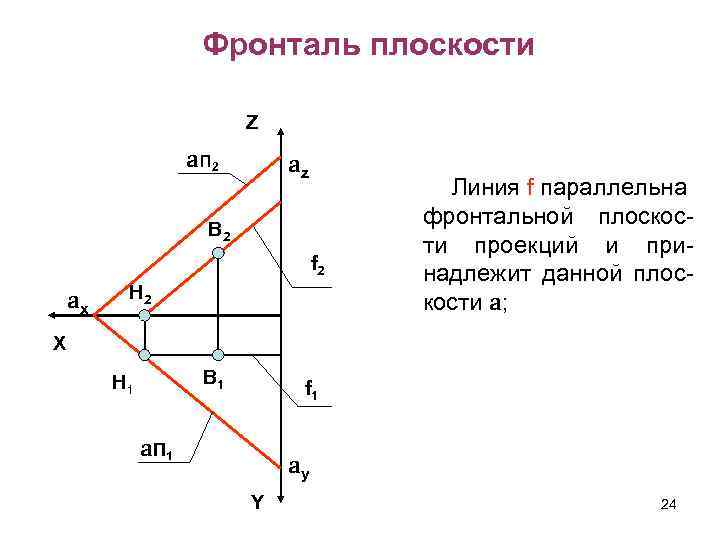Фронталь плоскости Z aп 2 az В 2 f 2 ax H 2 Линия f параллельна фронтальной плоскости проекций и принадлежит данной плоскости a; X В 1 H 1 f 1 a. П 1 ay Y 24

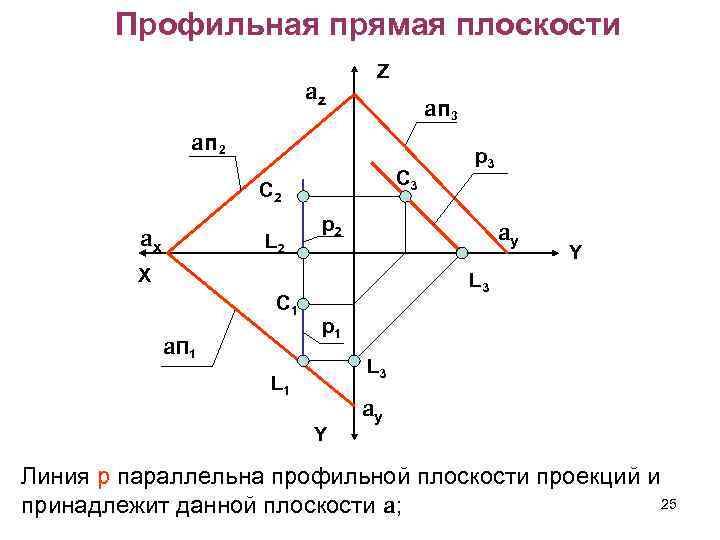Профильная прямая плоскости az Z aп 3 aп 2 С 3 С 2 ax L 2 р2 ay X С 1 a. П 1 р3 Y L 3 р1 L 3 L 1 Y ay Линия р параллельна профильной плоскости проекций и 25 принадлежит данной плоскости a;

Поверхности 26

ПОВЕРХНОСТИ ПОВЕРХНОСТЬ - МНОЖЕСТВО ПОЛОЖЕНИЙ ЛИНИИ ПЕРЕМЕЩАЮЩЕЙСЯ В ПРОСТРАНСТВЕ ПО ОПРЕДЕЛЕННОМУ ЗАКОНУ ЛИНИЯ ПЕРЕМЕЩАЮЩАЯСЯ В ПРОСТРАНСТВЕ НАЗЫВАЕТСЯ ОБРАЗУЮЩАЯ ЛИНИЯ ПО КОТОРОЙ ПРОИСХОДИТ ПЕРЕМЕЩЕНИЕ НАЗЫВАЕТСЯ НАПРАВЛЯЮЩАЯ 27

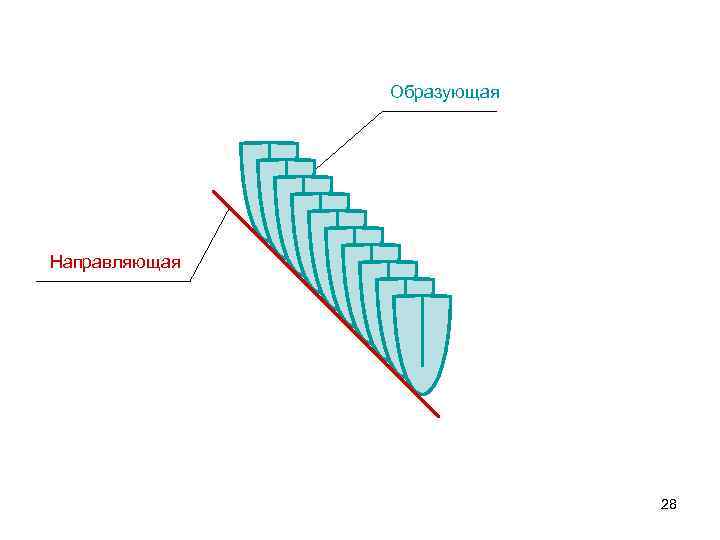Образующая Направляющая 28

СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ 1. АНАЛИТИЧЕСКИЙ – X 2 + Y 2 + Z 2 =1 2. ГРАФИЧЕСКИЙ: а. очерк б. каркас в. определитель 29

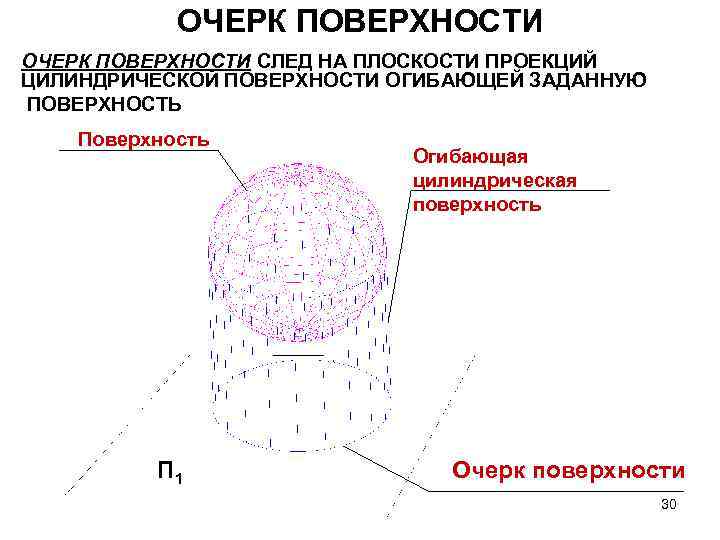ОЧЕРК ПОВЕРХНОСТИ СЛЕД НА ПЛОСКОСТИ ПРОЕКЦИЙ ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТИ ОГИБАЮЩЕЙ ЗАДАННУЮ ПОВЕРХНОСТЬ Поверхность П 1 Огибающая цилиндрическая поверхность Очерк поверхности 30

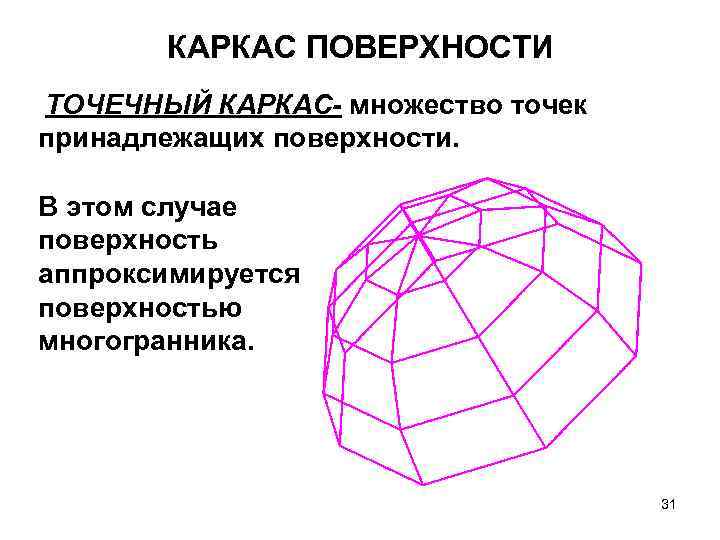КАРКАС ПОВЕРХНОСТИ ТОЧЕЧНЫЙ КАРКАС- множество точек принадлежащих поверхности. В этом случае поверхность аппроксимируется поверхностью многогранника. 31

ЛИНЕЙЧАТЫЙ КАРКАС – это множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит одна линия каркаса 32

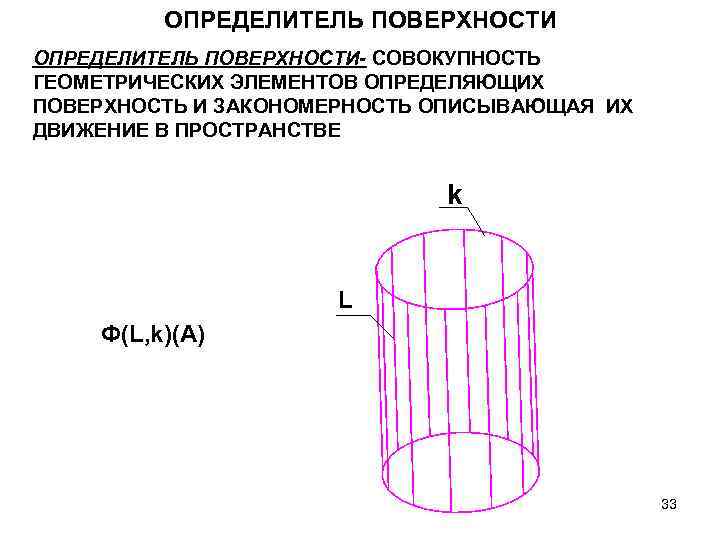ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ- СОВОКУПНОСТЬ ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ ОПРЕДЕЛЯЮЩИХ ПОВЕРХНОСТЬ И ЗАКОНОМЕРНОСТЬ ОПИСЫВАЮЩАЯ ИХ ДВИЖЕНИЕ В ПРОСТРАНСТВЕ k L Ф(L, k)(A) 33

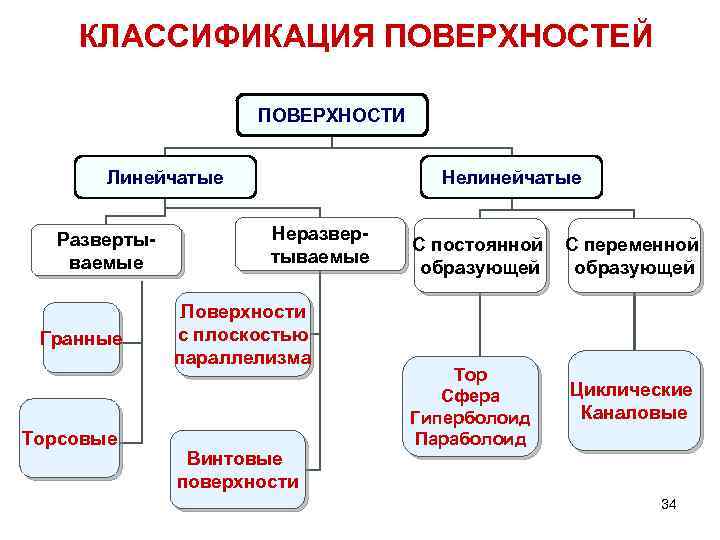КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ ПОВЕРХНОСТИ Линейчатые Нелинейчатые Неразвертываемые Развертываемые Поверхности с плоскостью параллелизма С постоянной образующей С переменной образующей П Гранные Торсовые Винтовые поверхности Тор Сфера Гиперболоид Параболоид Циклические Каналовые 34

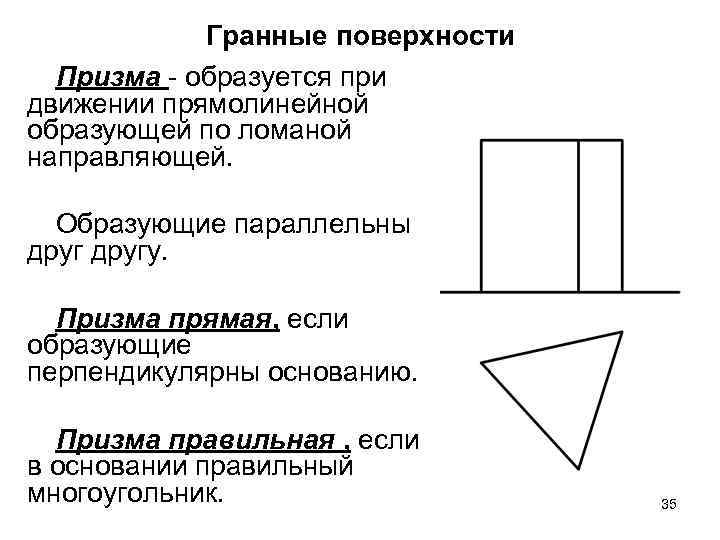Гранные поверхности Призма - образуется при движении прямолинейной образующей по ломаной направляющей. Образующие параллельны другу. Призма прямая, если образующие перпендикулярны основанию. Призма правильная , если в основании правильный многоугольник. 35

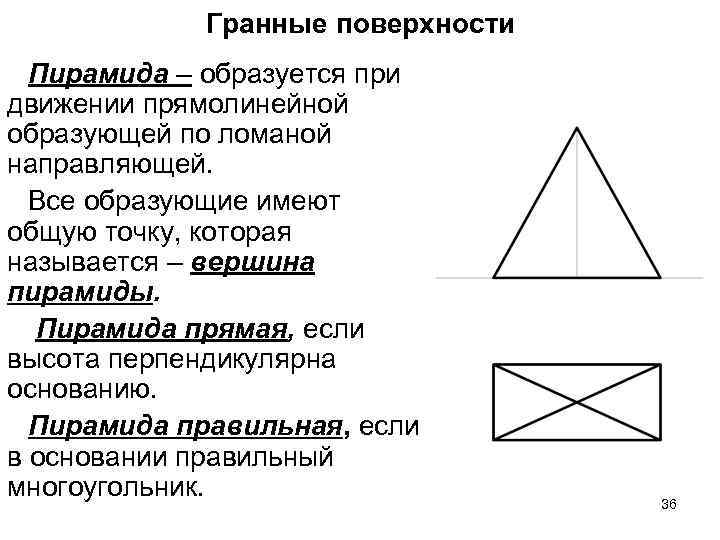Гранные поверхности Пирамида – образуется при движении прямолинейной образующей по ломаной направляющей. Все образующие имеют общую точку, которая называется – вершина пирамиды. Пирамида прямая, если высота перпендикулярна основанию. Пирамида правильная, если в основании правильный многоугольник. 36

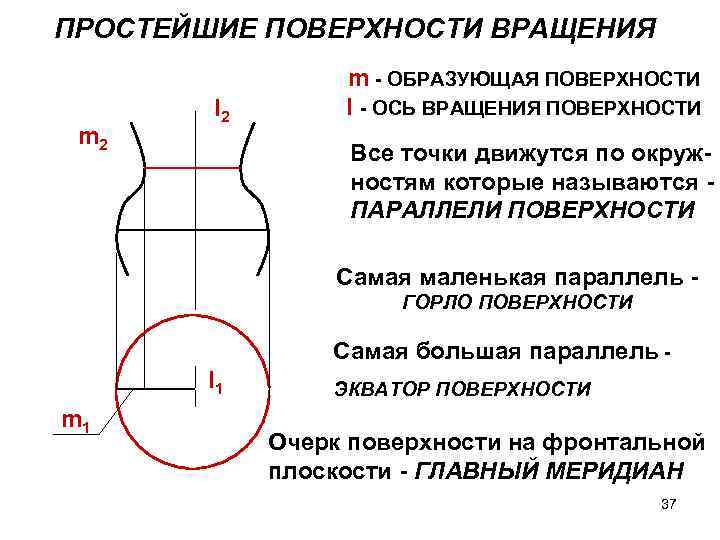ПРОСТЕЙШИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ m 2 I 2 m - ОБРАЗУЮЩАЯ ПОВЕРХНОСТИ I - ОСЬ ВРАЩЕНИЯ ПОВЕРХНОСТИ Все точки движутся по окружностям которые называются ПАРАЛЛЕЛИ ПОВЕРХНОСТИ Самая маленькая параллель ГОРЛО ПОВЕРХНОСТИ Самая большая параллель I 1 m 1 ЭКВАТОР ПОВЕРХНОСТИ Очерк поверхности на фронтальной плоскости - ГЛАВНЫЙ МЕРИДИАН 37

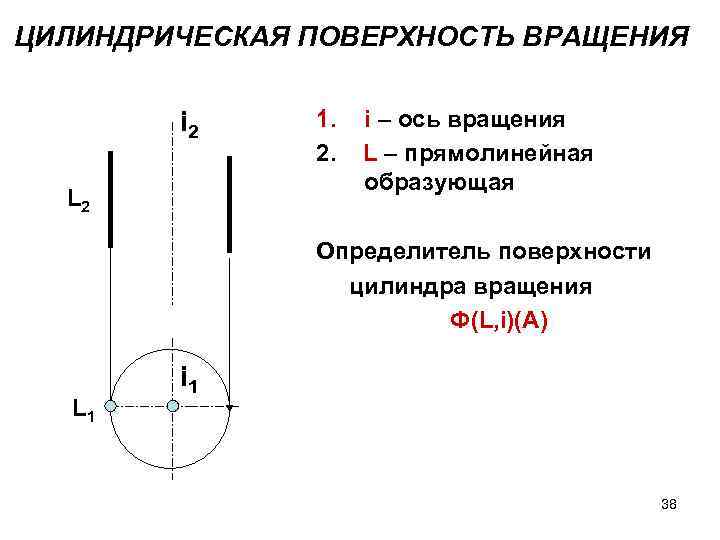ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ i 2 L 2 1. 2. i – ось вращения L – прямолинейная образующая Определитель поверхности цилиндра вращения Ф(L, i)(A) L 1 i 1 38

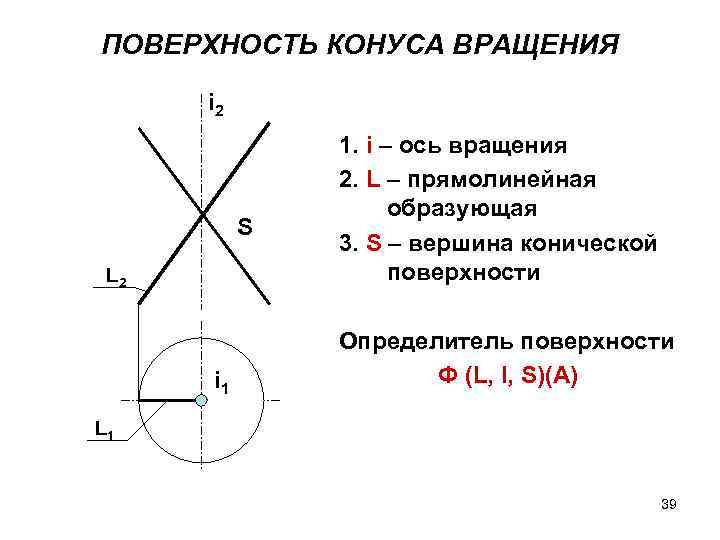ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ i 2 S L 2 i 1 1. i – ось вращения 2. L – прямолинейная образующая 3. S – вершина конической поверхности Определитель поверхности Ф (L, I, S)(A) L 1 39

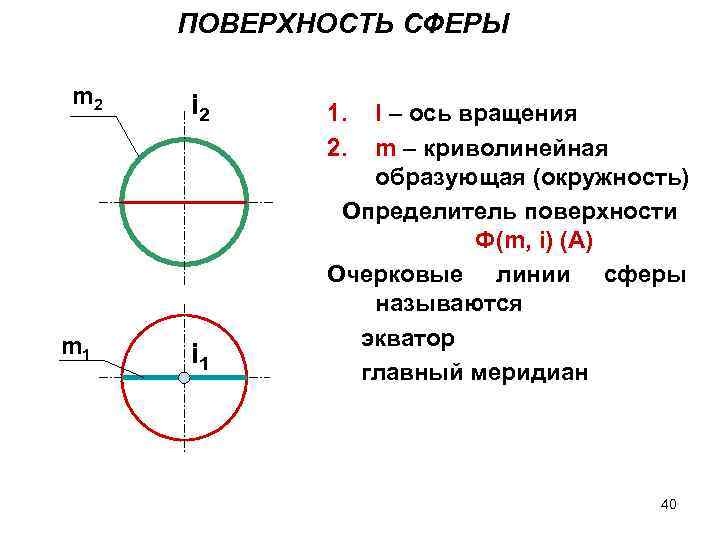ПОВЕРХНОСТЬ CФЕРЫ m 2 m 1 i 2 i 1 1. 2. I – ось вращения m – криволинейная образующая (окружность) Определитель поверхности Ф(m, i) (A) Очерковые линии сферы называются экватор главный меридиан 40

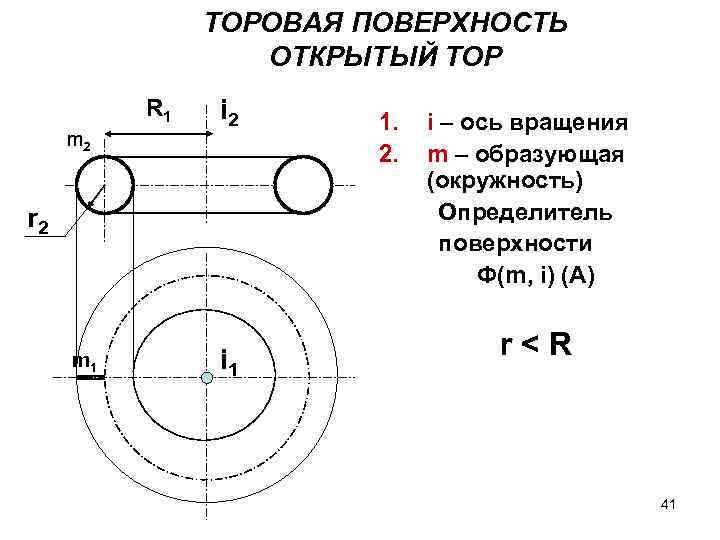ТОРОВАЯ ПОВЕРХНОСТЬ ОТКРЫТЫЙ ТОР R 1 m 2 i 2 r 2 m 1 i 1 1. 2. i – ось вращения m – образующая (окружность) Определитель поверхности Ф(m, i) (A) r

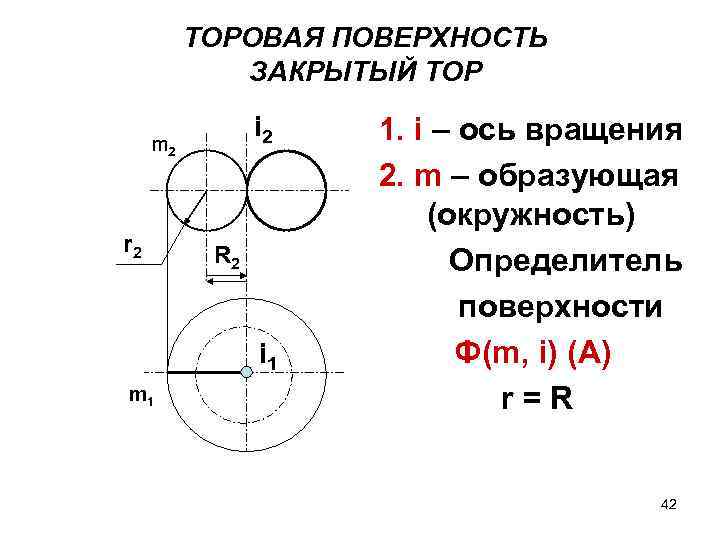ТОРОВАЯ ПОВЕРХНОСТЬ ЗАКРЫТЫЙ ТОР i 2 m 2 r 2 R 2 i 1 m 1 1. i – ось вращения 2. m – образующая (окружность) Определитель поверхности Ф(m, i) (A) r=R 42

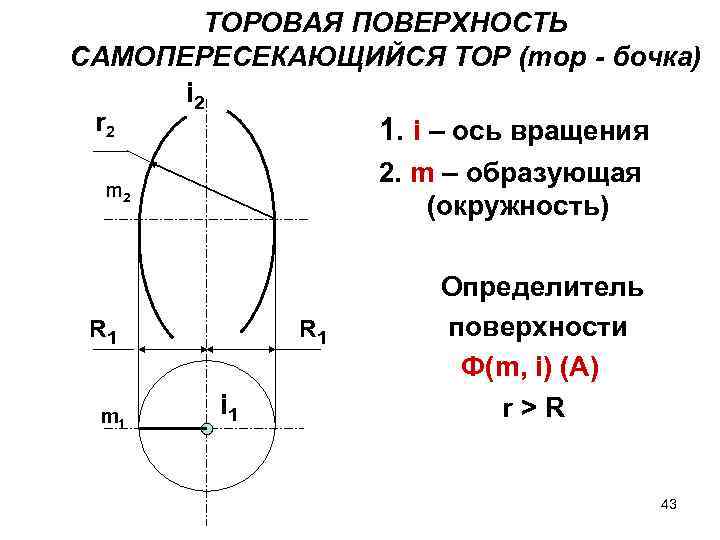ТОРОВАЯ ПОВЕРХНОСТЬ САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор - бочка) i 2 r 2 1. i – ось вращения 2. m – образующая m 2 (окружность) R 1 m 1 R 1 i 1 Определитель поверхности Ф(m, i) (A) r>R 43

Определение положения точек на поверхности тел 44

• Поверхность считается заданной на чертеже, если можно построить любую точку, ей принадлежащую. • Точка принадлежит поверхности, если она принадлежит какой- либо линии, принадлежащей этой поверхности. 45

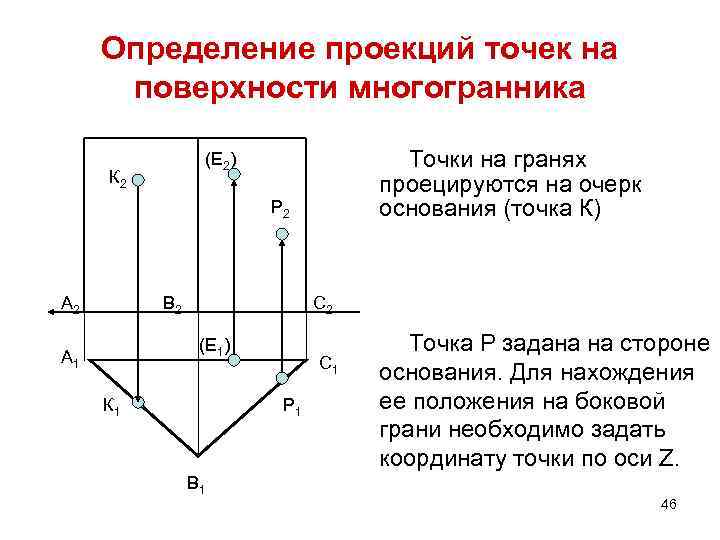Определение проекций точек на поверхности многогранника Точки на гранях проецируются на очерк основания (точка К) (Е 2) К 2 Р 2 А 2 В 2 С 2 (Е 1) А 1 К 1 С 1 Р 1 Точка Р задана на стороне основания. Для нахождения ее положения на боковой грани необходимо задать координату точки по оси Z. В 1 46

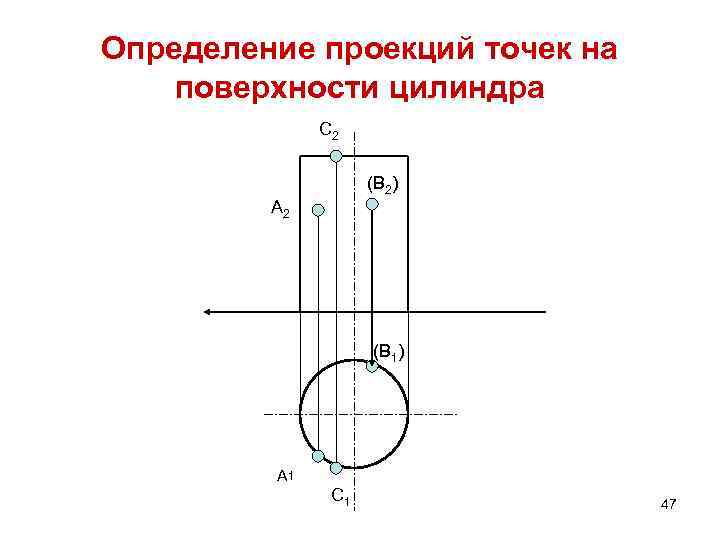Определение проекций точек на поверхности цилиндра С 2 (В 2) А 2 (В 1) А 1 С 1 47

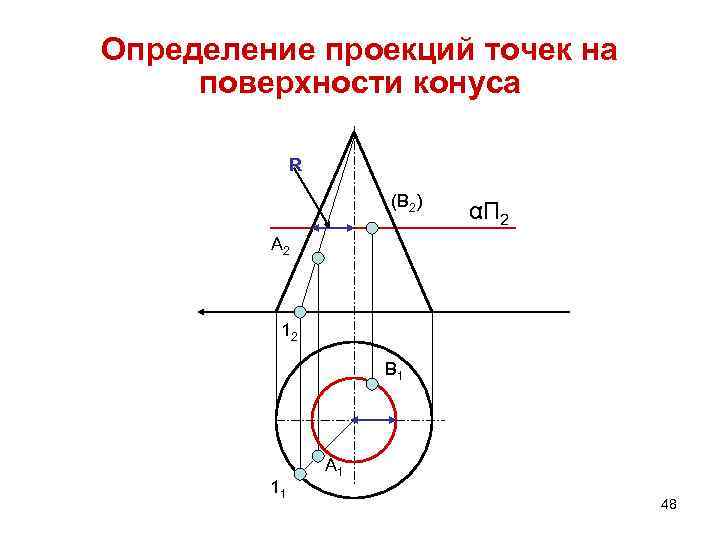Определение проекций точек на поверхности конуса R (В 2) αП 2 А 2 12 В 1 11 А 1 48

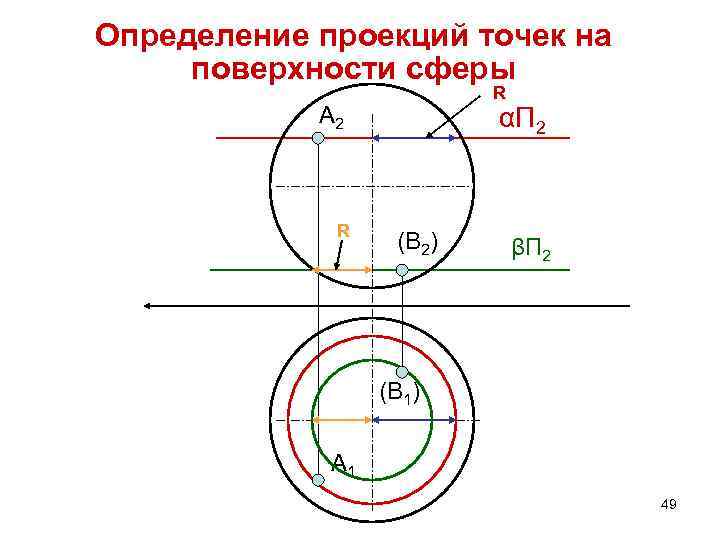Определение проекций точек на поверхности сферы R А 2 R αП 2 (В 2) βП 2 (В 1) A 1 49

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ ПРИ ПЕРЕСЕЧЕНИИ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ ПОЛУЧАЕТСЯ ЛИНИЯ, ВСЕ ТОЧКИ КОТОРОЙ ПРИНАДЛЕЖАТ КАК ПОВЕРХНОСТИ, ТАК И СЕКУЩЕЙ ПЛОСКОСТИ. Линия, ограничивающая полученную плоскую фигуру называется линией сечения. 50

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ • Если секущая плоскость параллельна плоскости проекций, то фигура сечения на плоскость проекций проецируется в натуральную величину. • Если секущая плоскость перпендикулярна плоскости проекций, то одна из проекций фигуры сечения прямая линия, совпадающая со следом плоскости. 51

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ Линия пересечения может быть: 1. ломаная - при пересечении плоскости и гранной поверхности; 2. плоская кривая - при пересечении плоскости с поверхностью вращения. 52

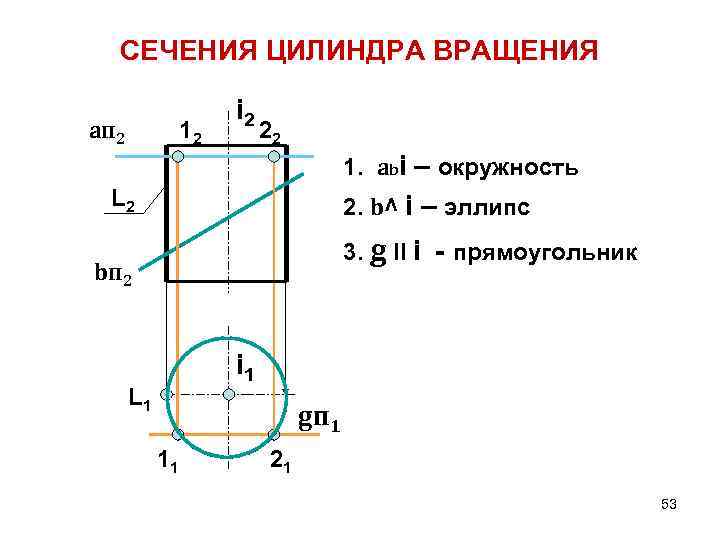СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ aп 2 12 i 2 22 1. abi – окружность L 2 2. b^ i – эллипс 3. g ll i - прямоугольник bп 2 i 1 L 1 gп 1 11 21 53

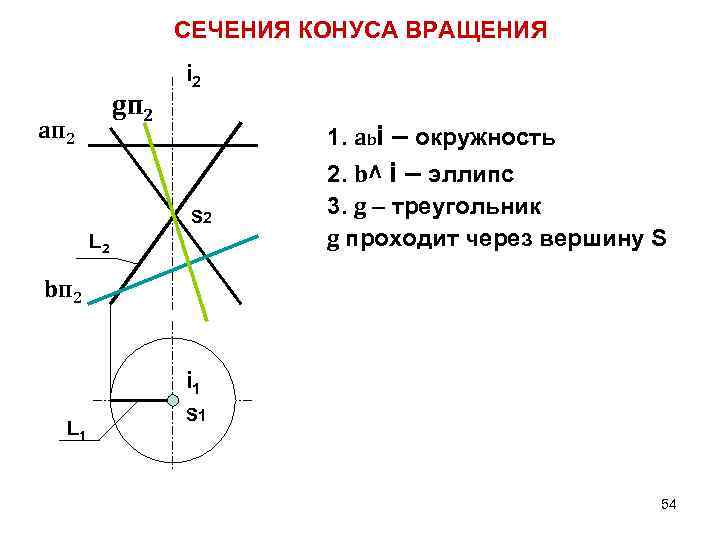СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ gп 2 aп 2 i 2 1. abi – окружность S 2 L 2 2. b^ i – эллипс 3. g – треугольник g проходит через вершину S bп 2 i 1 L 1 S 1 54

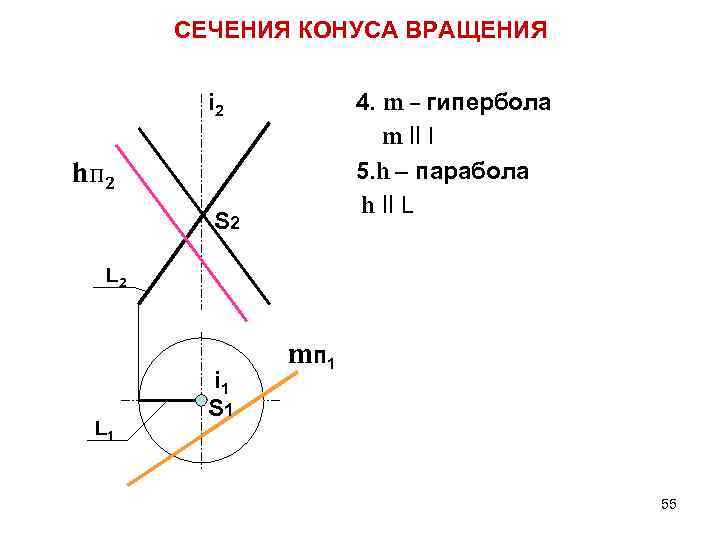СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ 4. m – гипербола m ll I 5. h – парабола h ll L i 2 hп 2 S 2 L 1 i 1 S 1 m п 1 55

ПОСТРОЕНИЕ СЕЧЕНИЯ 1. Определение секущей заданной плоскости. 2. Определить характерные точки: • точки, расположенные на крайних образующих; • точки, определяющие вершины кривых (эллипс - большую и малую ось, гипербола, парабола - вершины); • точки, определяющие видимость. 56

ПОСТРОЕНИЕ СЕЧЕНИЯ 3. Через выбранные точки провести вспомогательные секущие плоскости параллельно плоскостям проекций (в сечении окружность или прямоугольник). 4. Определить точки пересечения плоскости и построенного сечения. 57

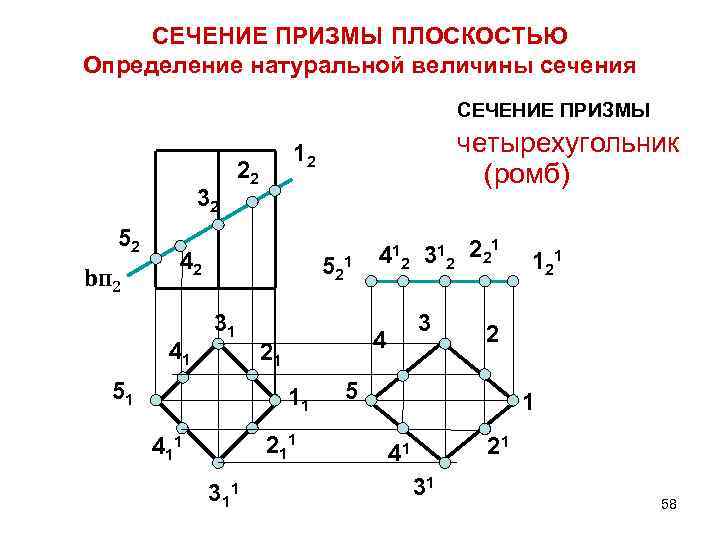СЕЧЕНИЕ ПРИЗМЫ ПЛОСКОСТЬЮ Определение натуральной величины сечения СЕЧЕНИЕ ПРИЗМЫ 32 52 bп 2 22 42 41 четырехугольник (ромб) 12 5 21 31 51 21 2 11 3 4 11 1 4 12 3 12 2 2 1 21 2 5 1 21 41 31 58

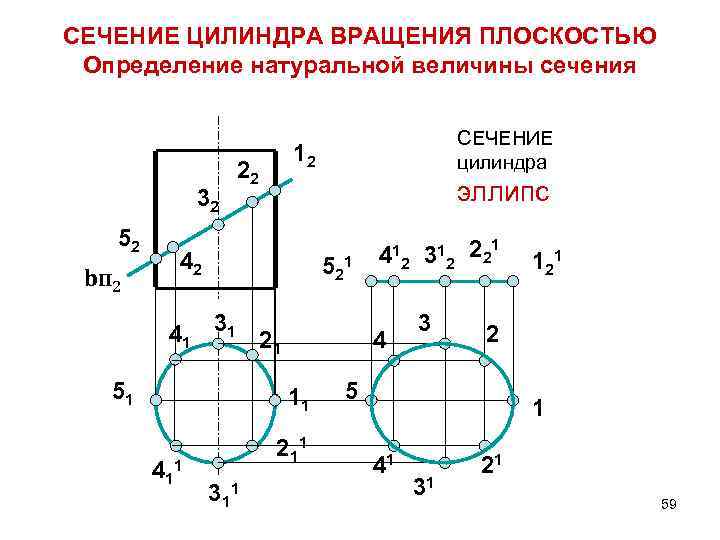СЕЧЕНИЕ ЦИЛИНДРА ВРАЩЕНИЯ ПЛОСКОСТЬЮ Определение натуральной величины сечения 32 52 bп 2 СЕЧЕНИЕ цилиндра 12 22 эллипс 42 5 21 41 31 21 51 4 11 2 11 3 11 1 4 12 3 12 2 2 3 1 21 2 5 1 41 31 21 59

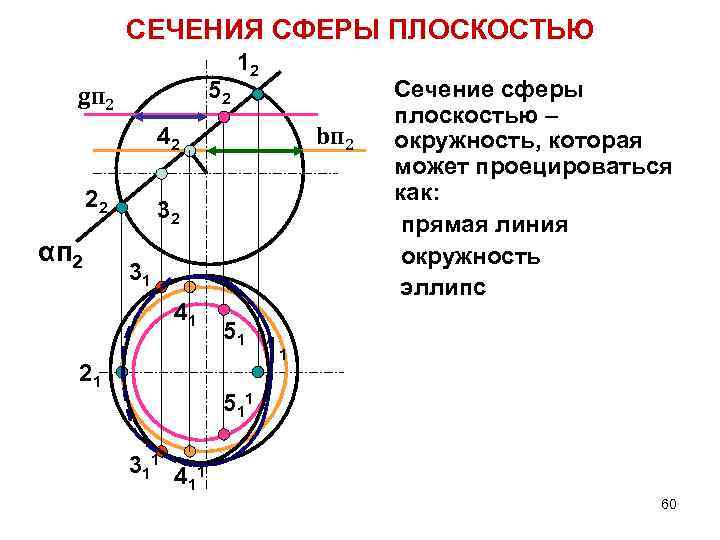СЕЧЕНИЯ СФЕРЫ ПЛОСКОСТЬЮ 52 gп 2 12 bп 2 42 22 αп 2 32 31 41 21 51 Сечение сферы плоскостью – окружность, которая может проецироваться как: прямая линия окружность эллипс 11 5 11 3 11 4 1 1 60

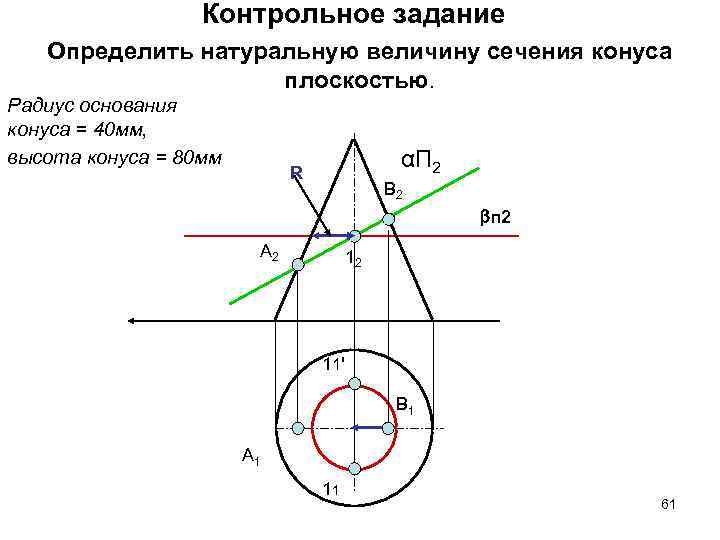Контрольное задание Определить натуральную величину сечения конуса плоскостью. Радиус основания конуса = 40 мм, высота конуса = 80 мм αП 2 R В 2 п 2 А 2 12 11' В 1 А 1 11 61

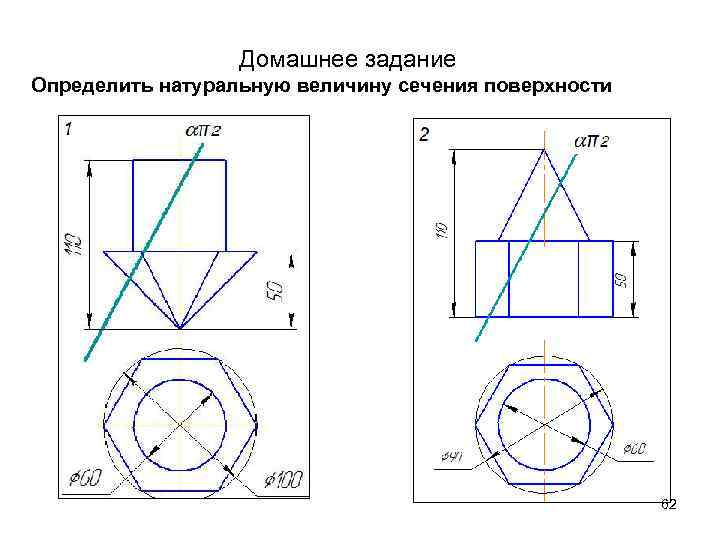Домашнее задание Определить натуральную величину сечения поверхности 62

Контрольные вопросы 1. Построить точку А(35, 10, 25). 2. Построить точку В(35, 10, 25). 3. Построить следы отрезка прямой АВ. А(35, 10, 25); В(60, 40, 10). 4. Название прямой перпендикулярной фронтальной плоскости проекций. 5. Название прямой, параллельной горизонтальной плоскости проекций. 63

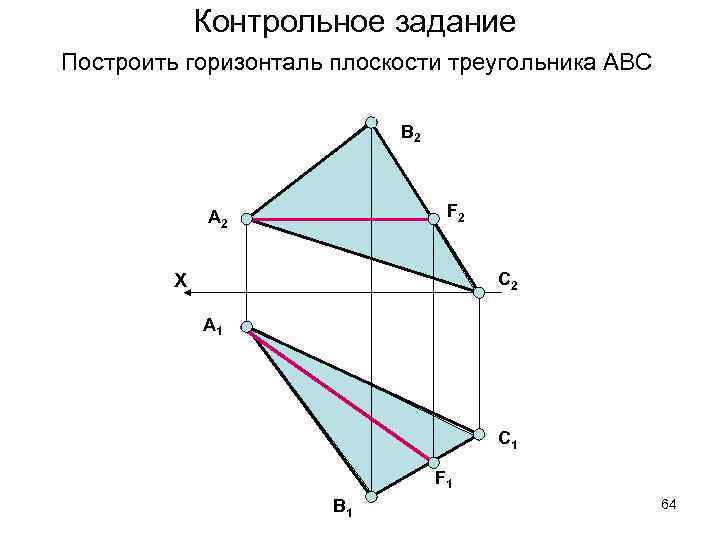Контрольное задание Построить горизонталь плоскости треугольника АВС В 2 F 2 А 2 С 2 X А 1 С 1 F 1 В 1 64

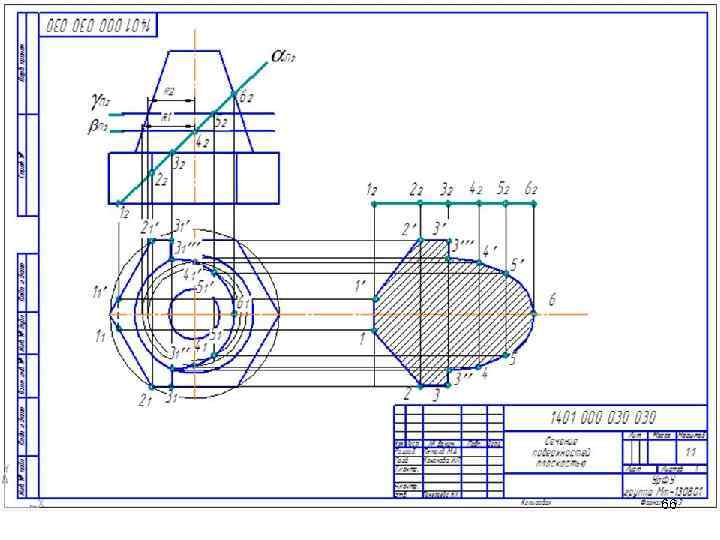
Домашнее задание Построить линию пересечения поверхностей. Определить натуральную величину сечения. Формат А 3. 65

66

Контрольные вопросы 1. Какие плоскости называют плоскостями уровня? 2. Построить горизонталь плоскости треугольника АВС. А(65, 10, 20); В(40, 50, 40); С(10, 25, 0). 67