Плоскость в пространстве
Плоскость в пространстве Общее уравнение плоскости Уравнение плоскости в отрезках Угол между двумя плоскостями Угол между прямой и плоскостью Расстояние от точки до плоскости Уравнение плоскости, проходящей через три точки
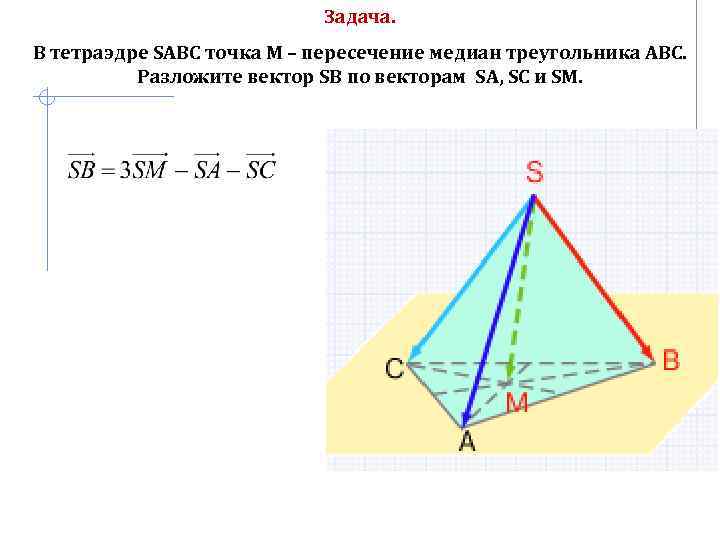
Задача. В тетраэдре SABC точка М – пересечение медиан треугольника АВС. Разложите вектор SB по векторам SA, SC и SM.
Общее уравнение плоскости Выведем уравнение плоскости, проходящей через точки М(x; y; z) и М 0 (х0; у0; z 0) М 0 М Значит перпендикулярен плоскости и, следовательно, любому вектору, лежащему в плоскости. Условие перпендикулярности двух векторов: Нормальный вектор плоскости Уравнение (1) можно записать в виде: Общее уравнение плоскости называется полным, если все Общее уравнение коэффициенты А; В; С; D отличны от нуля. плоскости В противном случае уравнение называется неполным.
Общее уравнение плоскости Виды неполных уравнений: 1) Плоскость проходит через точку н/к 2) z 3) 4) 5) 0 6) 7) 8) 9) 10) x y
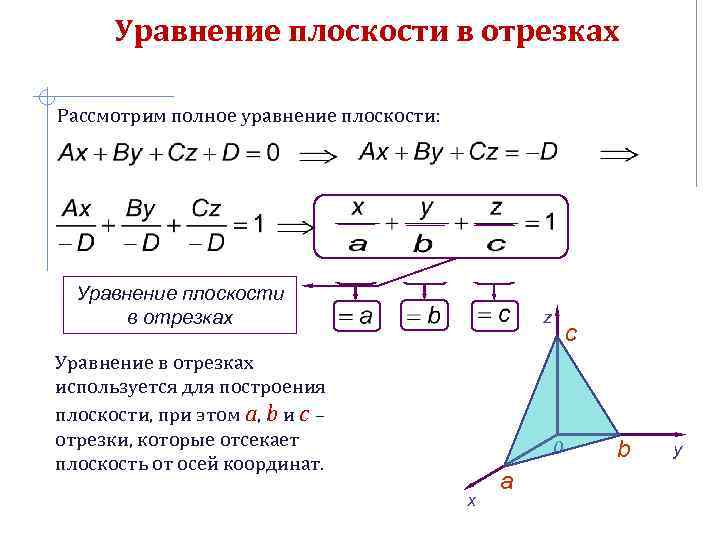
Уравнение плоскости в отрезках Рассмотрим полное уравнение плоскости: Уравнение плоскости в отрезках z Уравнение в отрезках используется для построения плоскости, при этом a, b и с – отрезки, которые отсекает плоскость от осей координат. с 0 x a b y
Угол между двумя плоскостями Пусть две плоскости заданы общими уравнениями: Углом между этими плоскостями называется угол между нормальными векторами к этим плоскостям.
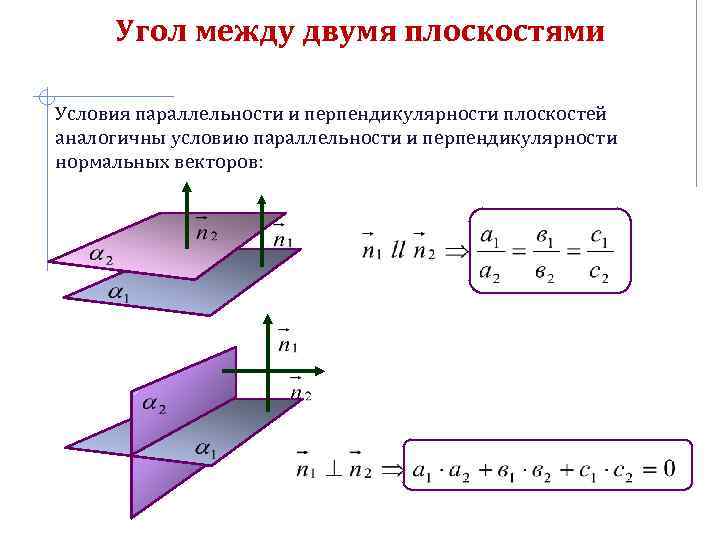
Угол между двумя плоскостями Условия параллельности и перпендикулярности плоскостей аналогичны условию параллельности и перпендикулярности нормальных векторов:
Угол между прямой и плоскостью Пусть точка М 1 – точка пересечения прямой р с плоскостью М М 1
Расстояние от точки до плоскости Пусть точка М 1(x 1; y 1; z 1) – основание перпендикуляра, опущенного из точки М 0(x 0; y 0; z 0) на плоскость М 0 М 1
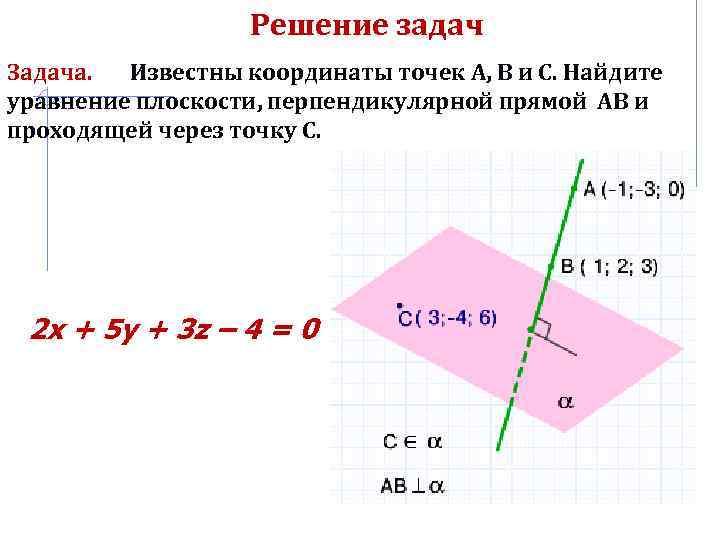
Решение задач Задача. Известны координаты точек А, В и С. Найдите уравнение плоскости, перпендикулярной прямой АВ и проходящей через точку С. 2 x + 5 y + 3 z – 4 = 0
Уравнение плоскости, проходящей через три точки Пусть точки М 1(х1 ; у1 ; z 1 ), М 2(х2 ; у2 ; z 2 ) и М 3(х3 ; у3 ; z 3 ) не лежат на одной прямой. Тогда векторы: и не коллинеарны. Точка М(х ; у ; z ) лежит в одной плоскости с точками М 1 , М 2 и М 3 только в том случае, если векторы: и Уравнение плоскости, проходящей через 3 точки М 3 М 1 М М 2 компланарны.
Скачать презентацию Плоскость в пространстве Плоскость в пространстве Общее
4уравнение плоскости.ppt