Плоский ротатор Семинар 6 r=L/2=const («жесткий») r жесткий

Плоский ротатор Семинар 6

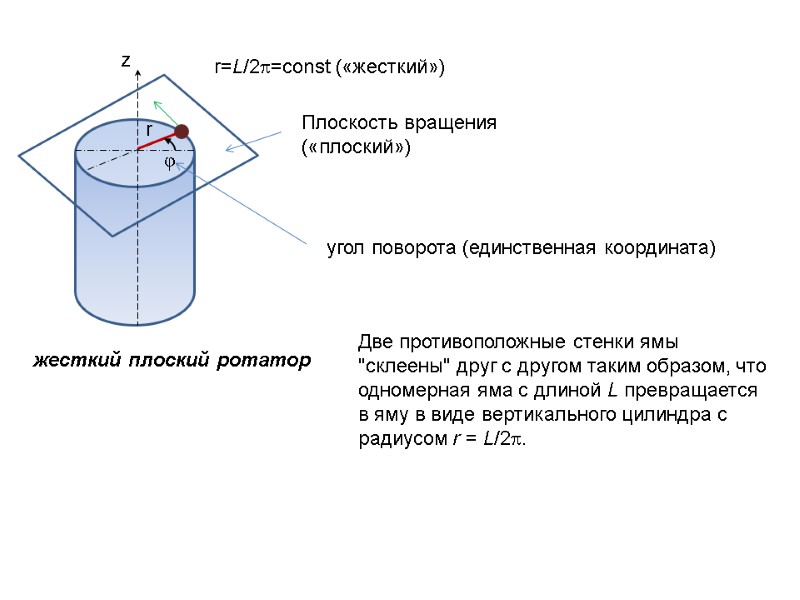
r=L/2=const («жесткий») r жесткий плоский ротатор z Плоскость вращения («плоский») φ угол поворота (единственная координата) Две противоположные стенки ямы "склеены" друг с другом таким образом, что одномерная яма с длиной L превращается в яму в виде вертикального цилиндра с радиусом r = L/2.

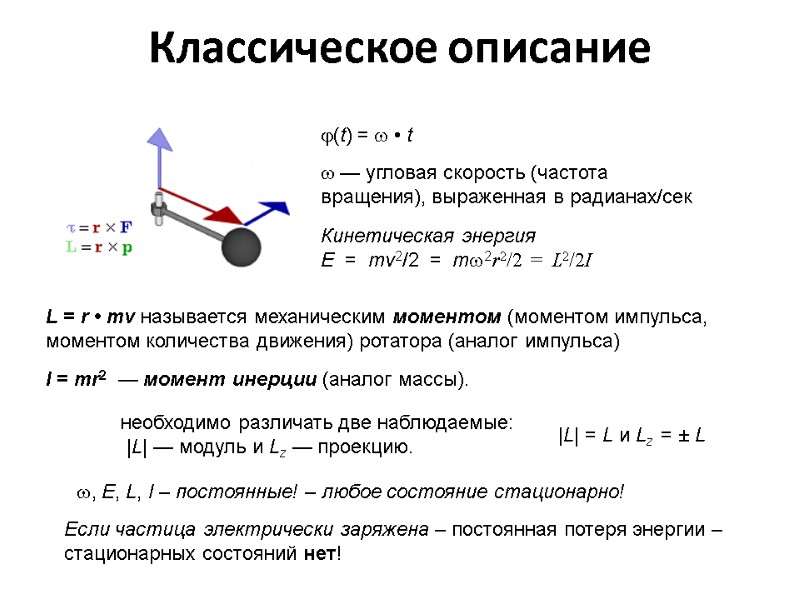
Классическое описание (t) =  • t  — угловая скорость (частота вращения), выраженная в радианах/сек Кинетическая энергия Е = mv2/2 = m2r2/2 = L2/2I L = r • mv называется механическим моментом (моментом импульса, моментом количества движения) ротатора (аналог импульса) I = mr2 — момент инерции (аналог массы). необходимо различать две наблюдаемые: |L| — модуль и Lz — проекцию. |L| = L и Lz = ± L , E, L, I – постоянные! – любое состояние стационарно! Если частица электрически заряжена – постоянная потеря энергии – стационарных состояний нет!

Квантовомеханическое описание Состояния ротатора должны описываться волновыми функциями Ф, зависящими только от одной пространственной переменной — угла . Ф(,t) = Ф() • eхр[i(E/h)t] Стационарные состояния Пространственная часть волновой функции должна подчиняться стационарному уравнению Шредингера: НФ() = ЕФ(). Ф() = Ае im + Be –im , где m = L/h решение

Как и в случае с потенциальным ящиком, в данном случае имеются определенные граничные условия: волновая функция должна в точности повторяться через каждое приращение аргумента (угла ) на величину 2: Ф() = Ф( + 2). Построим две функции для разных аргументов: Ф() = Ae im + Be –im Ф( + 2) = Aeim( + 2 ) + Be–im( + 2 ) = Aeimeim2 + Be–ime–im2 Требуемое равенство этих двух функций будет наблюдаться при условии: e im2 = e–im2 = 1 Комплексная экспонента равна 1 только тогда, когда ее фаза кратна 2: m • 2 = k • 2 , где k — любое целое число.

Константа m может иметь только целочисленные значения: m = 0, 1, 2, 3 . . . . . . , вследствие чего m называется вращательным квантовым числом. |L| = mh = 0, h , 2h , 3h . . . Lz = ± mh = 0, ±h , ±2h , ±3h . . . E = L2/2I = b • m2 = 0, b, 4b, 9b . . (здесь b = h2/2I — вращательная постоянная) Следовательно, учет граничных условий приводит к выделению некоторых разрешенных значений момента и энергии: энергетические уровни плоского ротатора являются двукратно вырожденными

Обратимся к рассмотрению волновых функций. Общее решение является суперпозицией двух частных решений: Ф() = Ае im + Be–im , где m = L/h для заданных значений наблюдаемых Е и L существует целое двумерное пространство стационарных состояний Один из базисов: Ф+() = С+ е im ( A = 1, B = 0 ) Ф– () = С– е–im ( A = 0, B = 1 ) Константы С+ и С– нужны для нормировки волновых функций (в данном случае они одинаковы и равны числу (1/2)1/2. В этих двух состояниях является строго определенным направление вращения частицы, а, следовательно, и ориентация вектора L, но совершенно неопределенна координата частицы!

Существуют, однако, некоторые суперпозиционные состояния, в которых пространственное положение частицы на окружности более определённо. B = A и Ф'() = А (е im + e–im ) , B = –A и Ф''() = А (е im – e–im ) . Применив тригонометрическое представление комплексных экспонент, найдем, что обе эти функции действительные: Ф'() = 2А cos (m) и Ф'' () = 2А sin (m) Для таких стационарных состояний вероятность найти частицу в некоторой определенной точке окружности уже будет зависеть от положения этой точки: P' () = (1/2) cos2 (m) P'' () = (1/2) sin2 (m) Частица "размазана" по окружности не совсем равномерно, а образует в некоторых областях более плотное облако, а в некоторых — менее плотное.

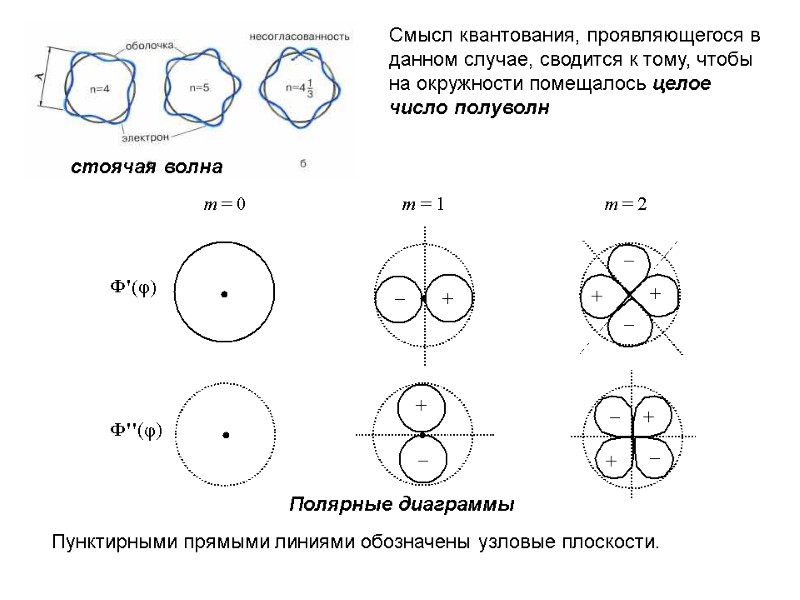
стоячая волна Полярные диаграммы Пунктирными прямыми линиями обозначены узловые плоскости. Смысл квантования, проявляющегося в данном случае, сводится к тому, чтобы на окружности помещалось целое число полуволн

Сферический ротатор   (, ) = () • () Существенное отличие сферического ротатора заключается в необходимости введения уже двух квантовых чисел:  — орбитальное квантовое число ( = 0, 1, 2 . . . .) m — магнитное квантовое число (m = 0, 1, 2 . . . l) | L |2 = h2[( + 1)] , где  = 0, 1, 2 , .... Е = | L |2 / 2I = (h2/2I) [( + 1)] = b [( + 1)] При заданном значении числа  магнитное число m может принимать только значения, не превосходящие по модулю число  (всего 2 +1 значение). Допустимые значения наблюдаемых задаются формулами:

Отличие! вектор L уже не обязан совпадать с осью вращения, и проекция этого вектора отличается от самого вектора. Дополнительное квантовое число m как раз и предназначено для определения величины проекции: Lz = m h сферический ротатор имеет дискретный набор стационарных состояний, расположенных на расходящейся системе энергетических уровней, однако степень вырождения каждого такого уровня иная, чем в случае плоского ротатора.

Каждому уровню энергии соответствует целое подпространство стационарных состояний размерности 2 + 1. У всех этих состояний модуль вектора L строго определен, но ориентация этого вектора является неопределенной.

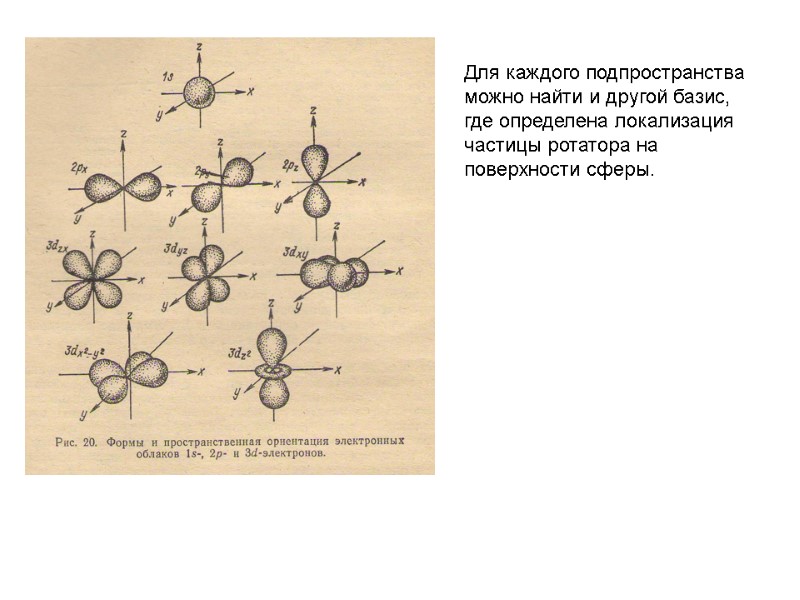
Для каждого подпространства можно найти и другой базис, где определена локализация частицы ротатора на поверхности сферы.

Сферический нежесткий ротатор В этой модели расстояние от частицы до центра вращения может изменяться, и в результате появляется еще одна степень свободы и еще одно квантовое число n (главное квантовое число). Конечный результат хорошо известен из теории одноэлектронного атома. Ансамбль ротаторов В случае, когда ротатор способен взаимодействовать с окружающей средой (термостатом), он уже не остается навсегда в одном из стационарных состояний, а пробегает все доступные ему стационарные состояния с вероятностями, определяемыми значениями энергии (в соответствии с функцией Больцмана).

Существенная особенность ротатора заключается в наличии вырождения энергетических уровней (особенно для сферического и нежесткого ротаторов). Это может привести к тому, что максимальная вероятность может приходиться не на самый низший уровень энергии, а на некоторый возбужденный. Так, например, для вращений молекул при комнатной температуре максимально заселенными являются уровни с вращательными числами  = 5 - 8.