Площадь Свойства площади Понятие площади многоугольника За

Площадь. Свойства площади.

Понятие площади многоугольника За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Если за единицу измерения отрезков принят сантиметр, то за единицу измерения площадей принимают квадрат со стороной 1 см. Такой квадрат называют квадратным сантиметром ( см² ) 1 га - площадь квадрата со стороной 100 м, 1 а ( сотка) = 100 м² 1 см 1 м² 1 м 1 мм² 1 мм

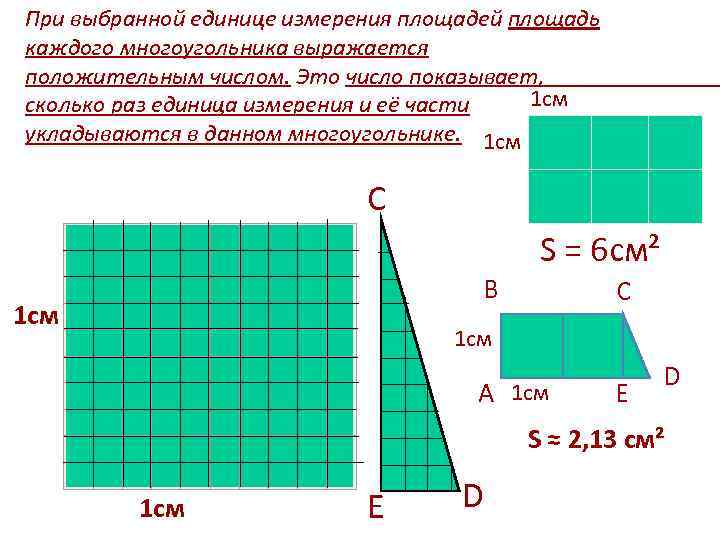При выбранной единице измерения площадей площадь каждого многоугольника выражается положительным числом. Это число показывает, 1 см сколько раз единица измерения и её части укладываются в данном многоугольнике. 1 см С S = 6 см² 1 см В С 1 см А 1 см E D S ≈ 2, 13 см² Е D

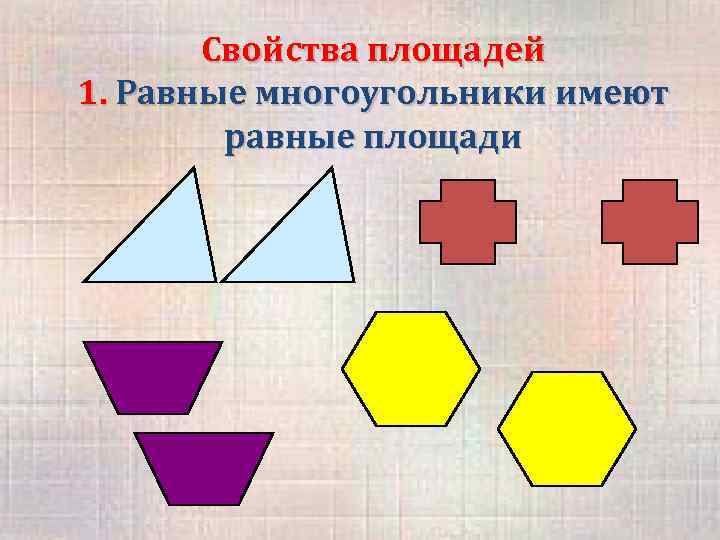Свойства площадей 1. Равные многоугольники имеют равные площади

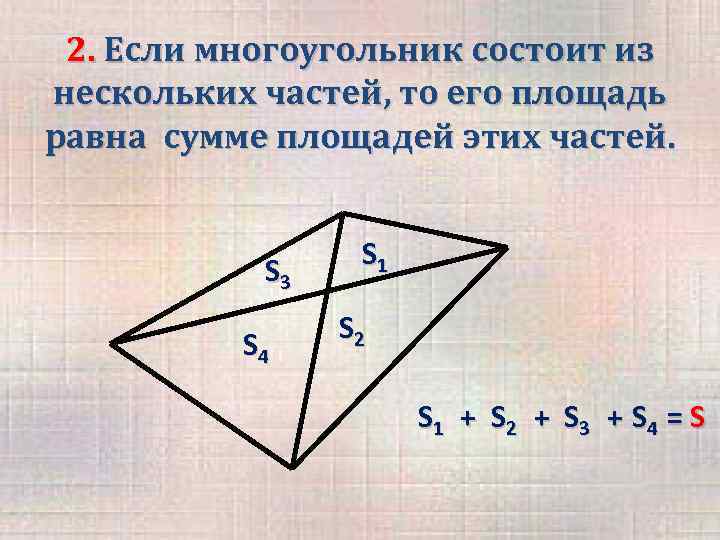2. Если многоугольник состоит из нескольких частей, то его площадь равна сумме площадей этих частей. S 3 S 4 S 1 S 2 S 1 + S 2 + S 3 + S 4 = S

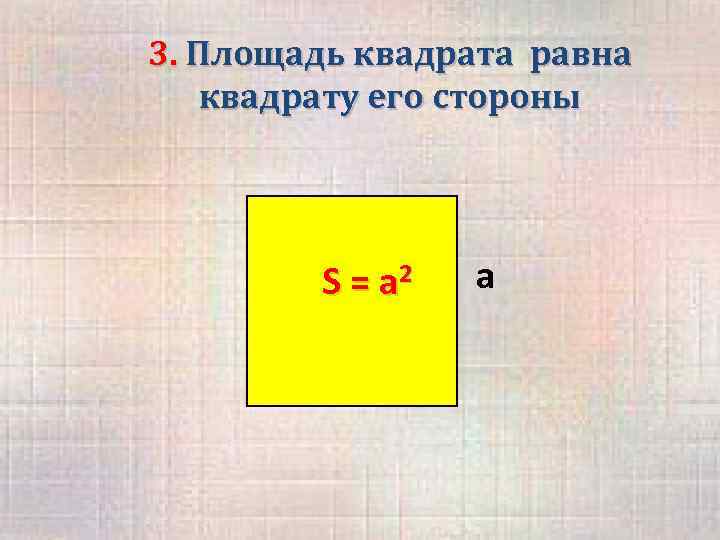3. Площадь квадрата равна квадрату его стороны S = а 2 а

Вычислите площадь каждой фигуры

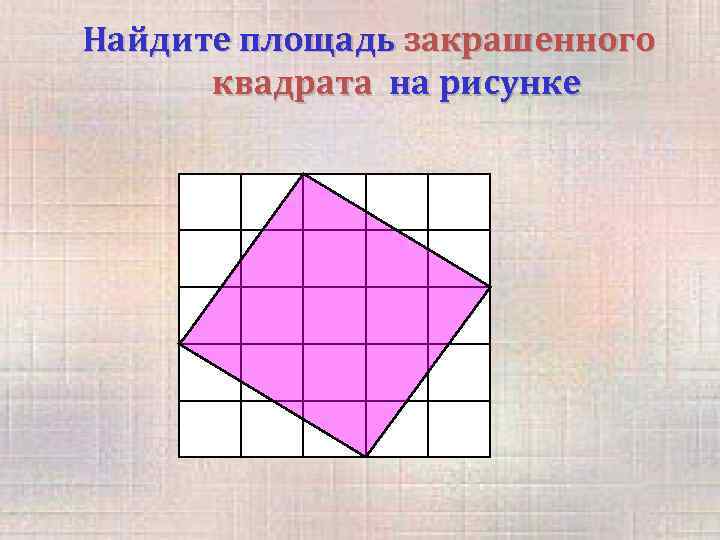Найдите площадь закрашенного квадрата на рисунке

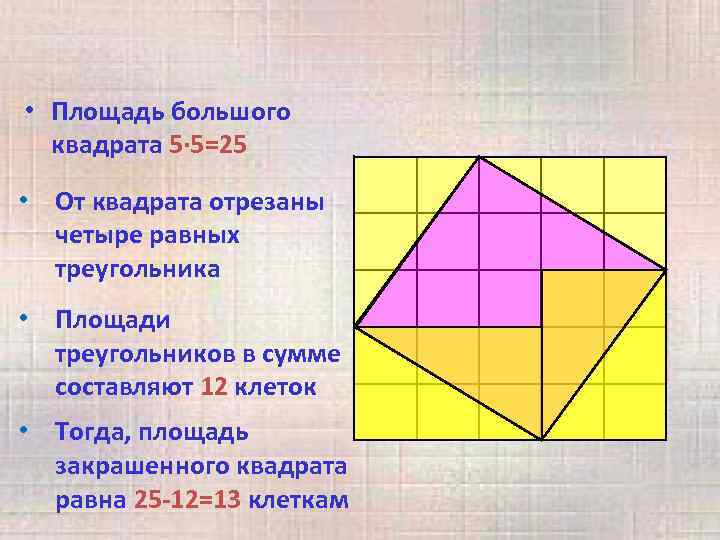• Площадь большого квадрата 5· 5=25 • От квадрата отрезаны четыре равных треугольника • Площади треугольников в сумме составляют 12 клеток • Тогда, площадь закрашенного квадрата равна 25 -12=13 клеткам

«Перекроите» прямоугольник в равнобедренный треугольник. Что сохранилось у прямоугольника и треугольника? Фигуры, имеющие одинаковые площади называются равновеликими

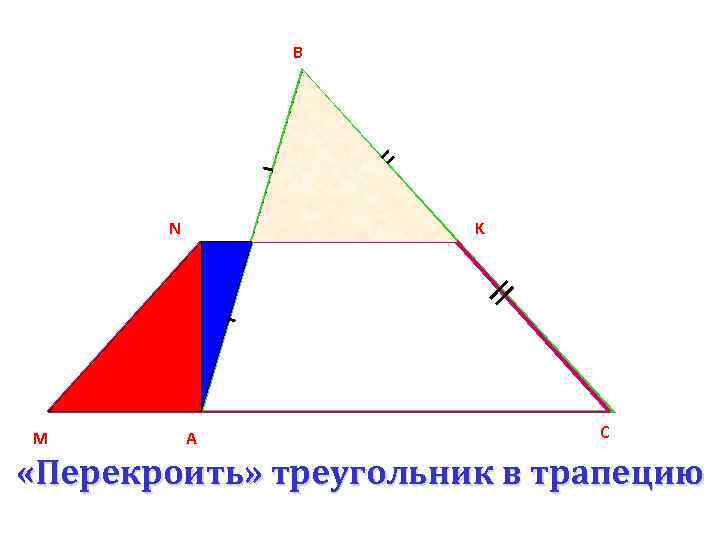В N М K А С «Перекроить» треугольник в трапецию

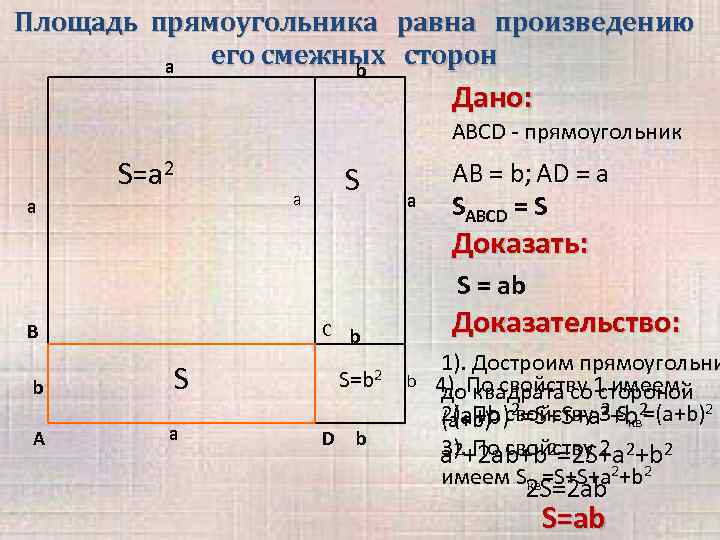Площадь прямоугольника равна произведению его смежных сторон a b Дано: ABCD - прямоугольник S=a 2 a S a a AB = b; AD = a SABCD = S Доказать: S = ab B C b S A a S=b 2 D Доказательство: b b b 1). Достроим прямоугольни 4). По свойству 1 имеем: до квадрата со стороной 2 2 2). По свойству 3 Sкв 2 (a+b) =S+S+a +b =(a+b) 3). По свойству 2 a 2+2 ab+b 2=2 S+a 2+b 2 имеем Sкв=S+S+a 2+b 2 2 S=2 ab S=ab

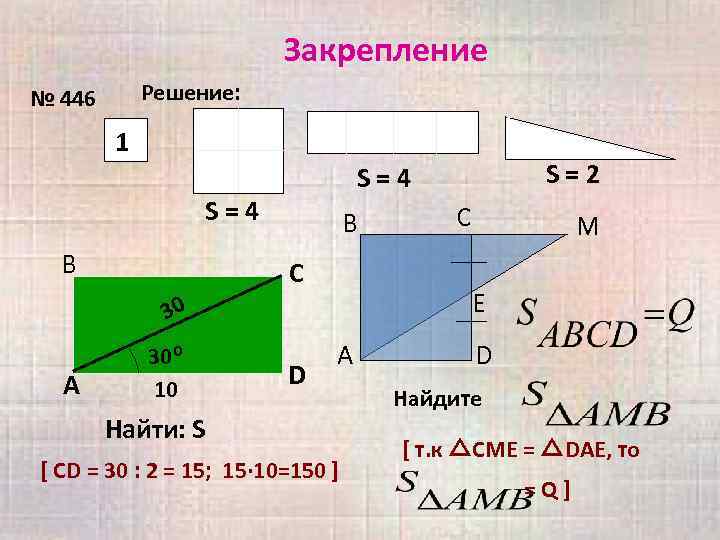Закрепление Решение: № 446 1 S=4 B В C A D C M E 30 30⁰ 10 S=2 S=4 А Найти: S [ CD = 30 : 2 = 15; 15· 10=150 ] D Найдите [ т. к △СМЕ = △DAE, то =Q]

Дома: П 48 -50. № 449(а); 450(а); 451.

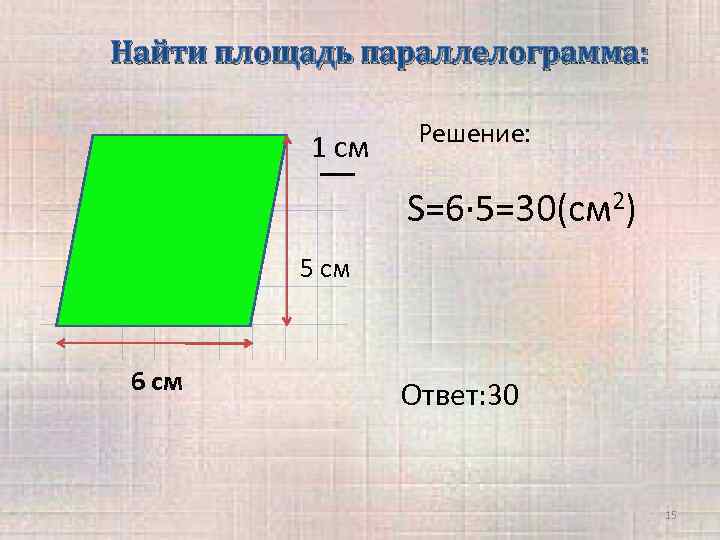Найти площадь параллелограмма: 1 см Решение: S=6· 5=30(cм 2) 5 см 6 см Ответ: 30 15