Плазма в електричному полі Провідність плазми Під дією

Плазма в електричному полі. Провідність плазми Під дією постійного електричного поля Е (за умови В = 0) в плазмі виникає направлений рух заряджених частинок – струм, густина якого де ui, ue – середні швидкості руху іонів та електронів вздовж вектора. Оскільки Під дією електричного поля перш за все починають прискорюватися електрони. В результаті виникає сила тертя з боку іонів, яка повинна компенсувати електричну силу: u – середня швидкість електронів, що встановилась в результаті балансу цих сил.

Окремо розглянемо випадки гарячої та холодної плазми. 1) Для гарячої плазми ( ) сила тертя (див. попер. лекцію): Враховуючи вирази для транспортного перерізу та частоти зіткнень які оцінюємо для теплової швидкості електронів, отримуємо: – середнє значення направленого імпульсу, що втрачається в кожному із зіткнень електронів з іонами (з частотою.

Слід відзначити, що відповідає середній направленій швидкості, тоді як – випадкова складова швидкості. При усередненні за проміжок часу, за який відбувається багато зіткнень, випадкова складова сили → 0 і залишається складова сили, що направлена проти швидкості. 2) Для холодної плазми ( ) частота зіткнень буде визначатися швидкістю направленого руху. В цьому випадку середня сила тертя (див. попер. лекцію): Таким чином, – гаряча плазма – холодна плазма

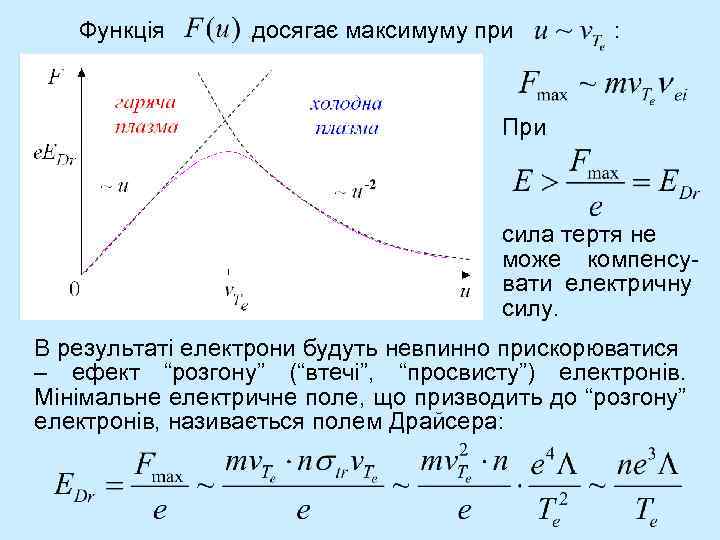Функція досягає максимуму при : При сила тертя не може компенсувати електричну силу. В результаті електрони будуть невпинно прискорюватися – ефект “розгону” (“втечі”, “просвисту”) електронів. Мінімальне електричне поле, що призводить до “розгону” електронів, називається полем Драйсера:

Інший вираз для поля Драйсера: Поле Драйсера – критичне поле для “розгону” основної групи електронів, що мають швидкість порядка теплової. Але й при плазма містить електрони із швидкістю, що значно перевищує теплову швидкість (т. з. максвелівський хвіст). Сила тертя на ці електрони мала і вони будуть прискорюватися навіть в полі, меншому за.

Направлена компонента швидкості , яку набирає електрон між двома зіткненнями з іонами, пропорційна , і, відповідно росте ~. При достатньо великій швидкості теплового руху направлена швидкість може досягнути величини того ж порядку, що й , чи навіть її перевищити. В такій ситуації спрощена модель, згідно з якою електрон набирає на довжині пробігу невелику направлену швидкість і повністю її втрачає при сильному зіткненні, непридатна. В дійсності прискорення і гальмування електрона відбувається одночасно. Поки електрон набирає швидкість, резерфордівське розсіяння на іонах поступово змінює напрямок його руху. Електричне поле намагається випрямити траєкторію руху, в той час як взаємодія з іонами її згинає. Якщо приріст направленої компоненти швидкості не компенсується розсіянням, то рівновага сил не може встановитися і електрон переходить в процес безперервного прискорення.

Із збільшенням енергії сила гальмування спадає і електрон в стані “розгону” буде прискорюватися до тих пір, поки він знаходиться в цьому полі. В стан “розгону” полем переходять ті електрони, які встигають набрати на довжині вільного пробігу λ додаткову направлену швидкість u, що перевищує їх початкову швидкість v. T. Умова “розгону”: Для водневої плазми: Така умова задовольняється для електронів з We >> Te.

Провідність плазми З балансу електричної сили і сили тертя отримуємо: – закон Ома для Е = const, B = 0. Малое внешнее поле Е ускоряет электроны до тех пор, пока сила трения об ионы не уравновесит электрическую силу.

Провідність плазми Електропровідність плазми: З використанням виразу для плазмової (Ленгмюрівської) частоти ω0 отримуємо:

Інший важливий вираз для провідності: Провідність повністю іонізованої водневої плазми швидко зростає при збільшенні температури і практично не залежить (слабка залежність через Λ) від густини n.

Практична формула для розрахунку (формула Спітцера): Формула Спитцера (американський фізик) Оскільки Λ ≈ 15 :

Легко переконатися, що термоядерна плазма є кращим провідником, ніж мідь. Для багатокомпонентної плазми (Z 1, … , Zn): де αk – парціальні концентрації іонів із зарядом Zk. Наявність багатозарядних іонів значно знижує провідність плазми.

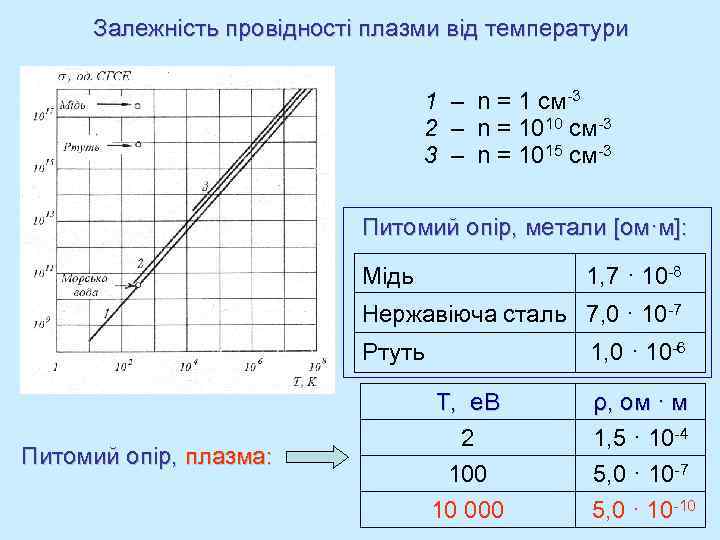Залежність провідності плазми від температури 1 – n = 1 см-3 2 – n = 1010 см-3 3 – n = 1015 см-3 Питомий опір, метали [ом·м]: Мідь 1, 7 · 10 -8 Нержавіюча сталь 7, 0 · 10 -7 Ртуть Питомий опір, плазма: 1, 0 · 10 -6 Т, е. В 2 100 10 000 ρ, ρ, ом · м 1, 5 · 10 -4 5, 0 · 10 -7 5, 0 · 10 -10

Електричне поле E(t) ≠ const В електричному полі високої частоти суттєве значення має механічна інерція електронів. Нехай напруженість поля: а х – зміщення електрона вздовж вектора Рівняння руху : Розв’язок: .

Густина струму: – провідність. Дійсна та уявна частини провідності: У випадку постійного електричного поля (ω = 0) маємо раніше отриманий вираз (слайд 9):

У випадку електричного поля високої частоти впливом процесу зіткнень можна знехтувати. При νei << ω провідність стає чисто уявною: Струм запізнюється по фазі відносно напруженості на 90º – інерція електронів.