a0c70c3cea6c70f2052b43888cd5888b.ppt
- Количество слайдов: 22

Platonic Solids

Plato (427 BC – 347 BC) • Greek philosepher • 387 BC based a school in Athina • Died 80 years old

Archeological discovery from Scotland 2000 BC

Platonic Solids in the antic

Johannes Kepler (27. 12. 1571 Weil der Stadt – 15. 11. 1630 Regensburg) • German mathematican and astronomer • Several years lived in Prague as a guest of Rudolf II
Karlova ulice 4, Prague, house of Johannes Kepler
Solar System Model

Platonic Solid • Convex polyhedron • All faces are equal regular polygon (K vertecies) • In each vertex of the polyhedron the same number of edges intersects (L edges)

Which Platonic Solids exist? • • V … number of vertecies F … number of faces E … number of edges Euler formula: For each convex polyhedron V + F = E +2

Which Platonic Solids exist? • The conditions of Platonic Solids – K. F = 2. E – L. V = 2. E F = 2 E/K V = 2 E/L • Substitution into Euler formula 2 E/L + 2 E/K = E +2 1/L + 1/K = 1/E + 1/2

For which numbers holds 1/K+1/L = 1/E +1/2 • K and L are integers bigger or equal to 3 • For K = 3 – – L=3, E=6: 1/3+1/3 = 1/6+1/2 L=4, E=12: 1/3+1/4 = 1/12+1/2 L=5, E=30: 1/3+1/5 = 1/30+1/2 For L=>6 not possible • For K = 4 – L=3, E=12: 1/4+1/3 = 1/12+1/2 – For L=>4 not possible • For K = 5 – L=3, E=30: 1/5+1/3 = 1/30+1/2 – Pro L=>4 not possible • For K => 6 not possible even for L=3
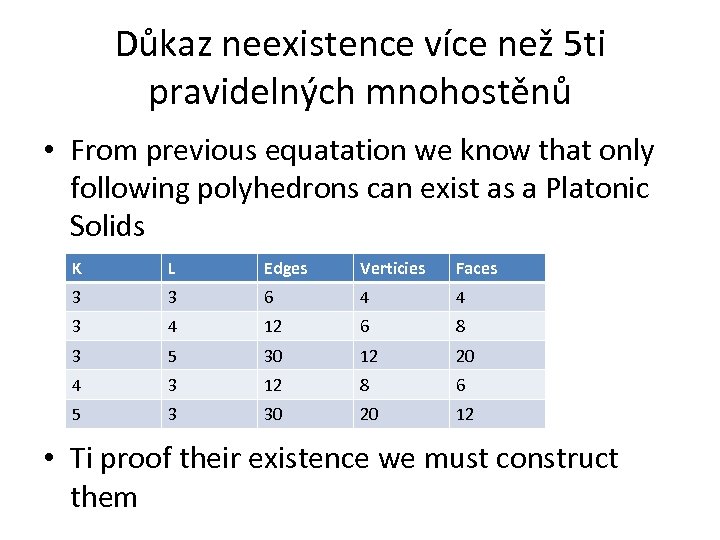
Důkaz neexistence více než 5 ti pravidelných mnohostěnů • From previous equatation we know that only following polyhedrons can exist as a Platonic Solids K L Edges Verticies Faces 3 3 6 4 4 3 4 12 6 8 3 5 30 12 20 4 3 12 8 6 5 3 30 20 12 • Ti proof their existence we must construct them

Regular Tetrahedron • 4 3 -angle faces, 4 verticies, in each 3 edges, total 6 edges

Regular Tetrahedron • 4 3 -angle faces, 4 verticies, in each 3 edges, total 6 edges

Regular Octahedron • 8 3 -angle faces, 6 verticies, in each 4 edges, total 12 edges
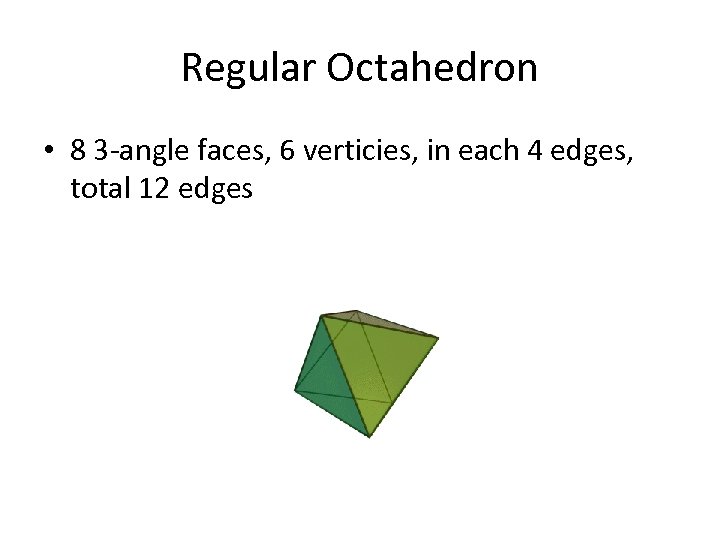
Regular Octahedron • 8 3 -angle faces, 6 verticies, in each 4 edges, total 12 edges

Regular Isosahedron • 20 3 -angle faces, 12 vertecies, in each 5 edges, total 30 edges
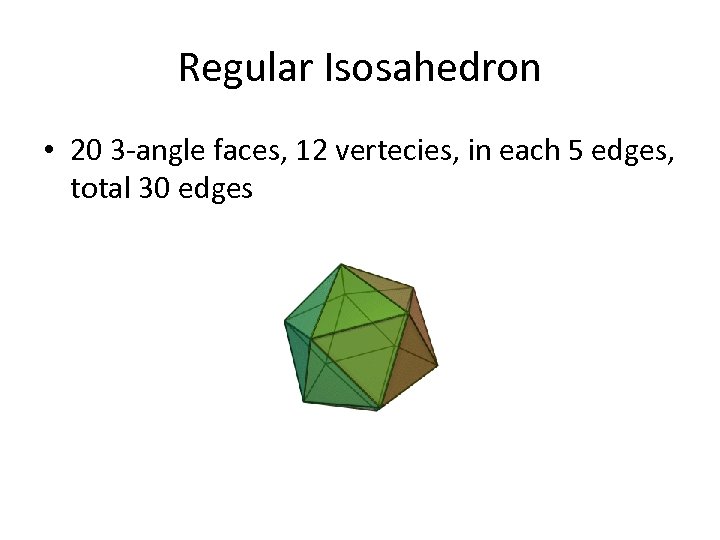
Regular Isosahedron • 20 3 -angle faces, 12 vertecies, in each 5 edges, total 30 edges

Regular 6 -hedron • 6 4 -angle faces, 8 vertecies, in each 3 edges, total 12 edges

Cube • 6 4 -angle faces, 8 vertecies, in each 3 edges, total 12 edges

Regular Dodecahedron • 12 5 -angle faces, 20 vertecies, in each 3 edges, total 30 edges
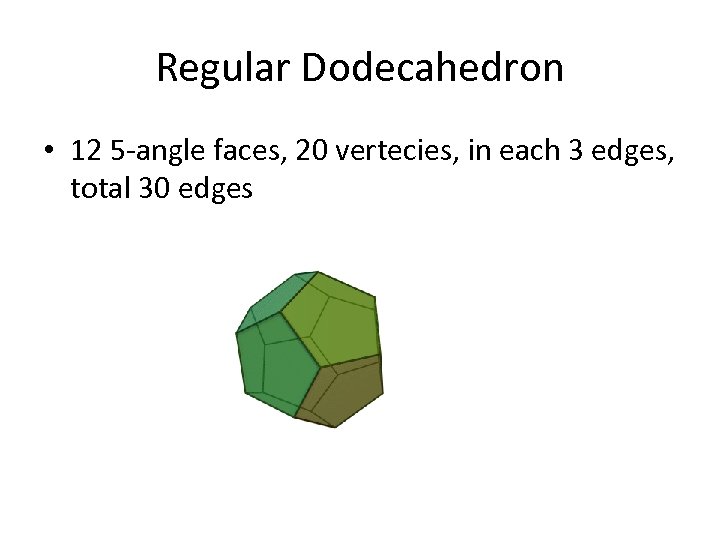
Regular Dodecahedron • 12 5 -angle faces, 20 vertecies, in each 3 edges, total 30 edges
a0c70c3cea6c70f2052b43888cd5888b.ppt