Plasma Heating Dirk Hartmann IPP Summer School IPP

Plasma Heating Dirk Hartmann IPP Summer School IPP Garching, September 20, 2001

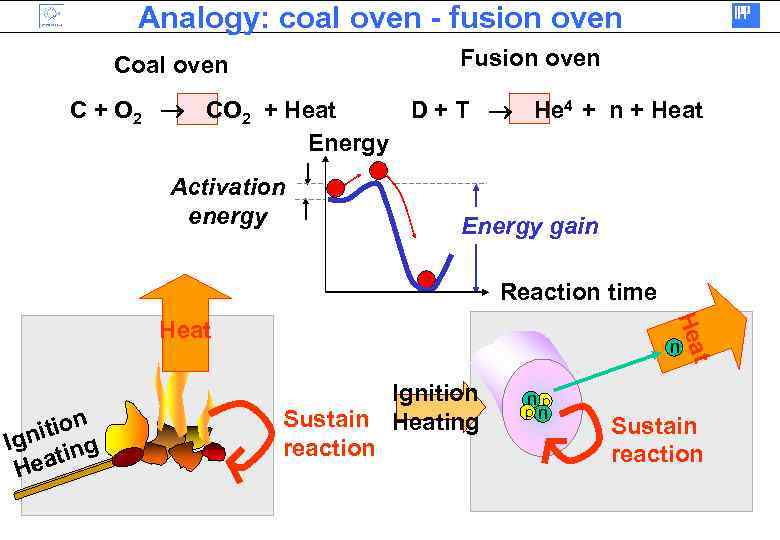Analogy: coal oven - fusion oven Fusion oven Coal oven C + O 2 CO 2 + Heat D + T He 4 + n + Heat Energy Activation energy Energy gain Reaction time Heat n t ition Ign ing t Hea Ignition Sustain Heating reaction np pn Sustain reaction

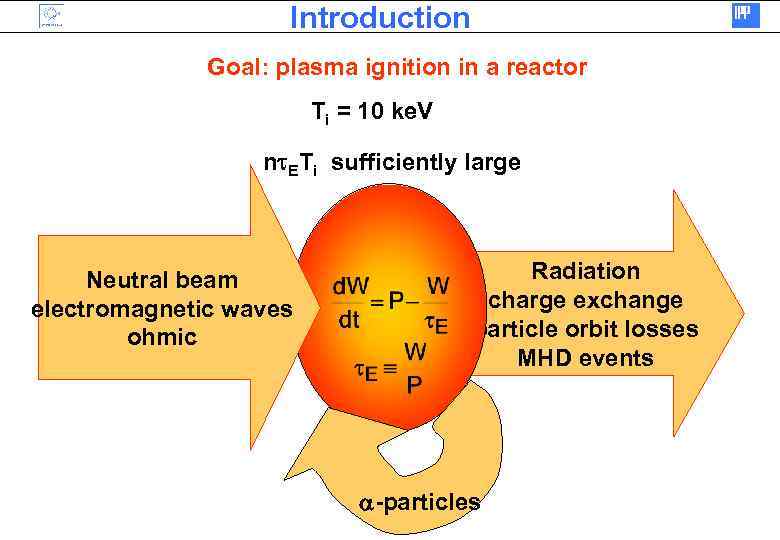Introduction Goal: plasma ignition in a reactor Ti = 10 ke. V nt. ETi sufficiently large Neutral beam electromagnetic waves ohmic Radiation charge exchange particle orbit losses MHD events a-particles

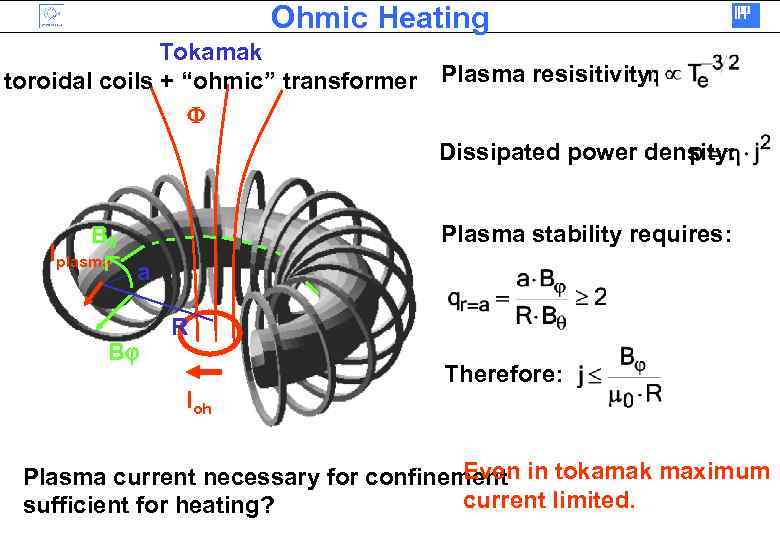Ohmic Heating Tokamak toroidal coils + “ohmic” transformer F Plasma resisitivity: Dissipated power density: Plasma stability requires: Bq Iplasma a Bj R Ioh Therefore: Even Plasma current necessary for confinement in tokamak maximum current limited. sufficient for heating?

Ohmic Heating Dominant loss mechanism: bremsstrahlung loss power pb. Ohmic heating power: Ohmic heating alone: Te only a few ke. V need additional heating power!

The need for plasma heating In fusion reactor: provide initial heating for ignition influence plasma properties 50 -100 M 20 MW In experiments: <40 MW sustain plasmas at relevant T simulate a-particle heating study plasma transport properties Neutral Beam Injection heating of plasma io Ion Cyclotron Resonance Heating heating of ions and e Lower Hybrid Heating heating of electrons, Electron Cyclotron Resonance Heating heating of electrons a-particle Heating mainly electrons

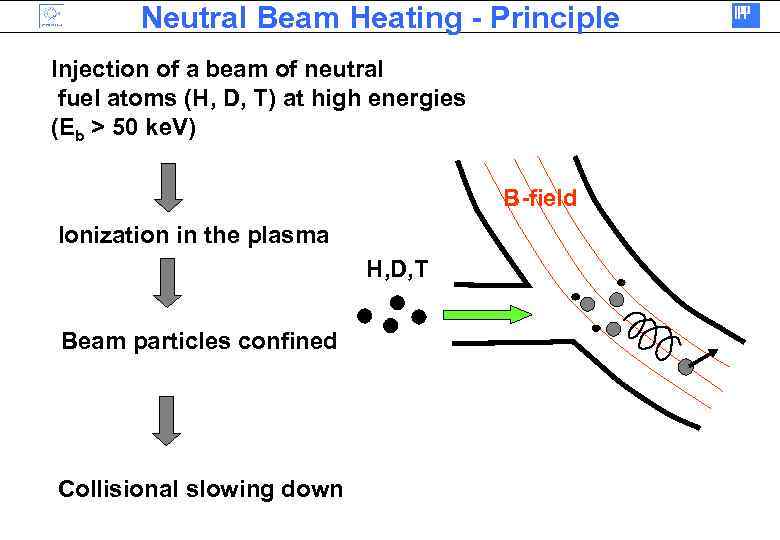Neutral Beam Heating - Principle Injection of a beam of neutral fuel atoms (H, D, T) at high energies (Eb > 50 ke. V) B-field Ionization in the plasma H, D, T Beam particles confined Collisional slowing down

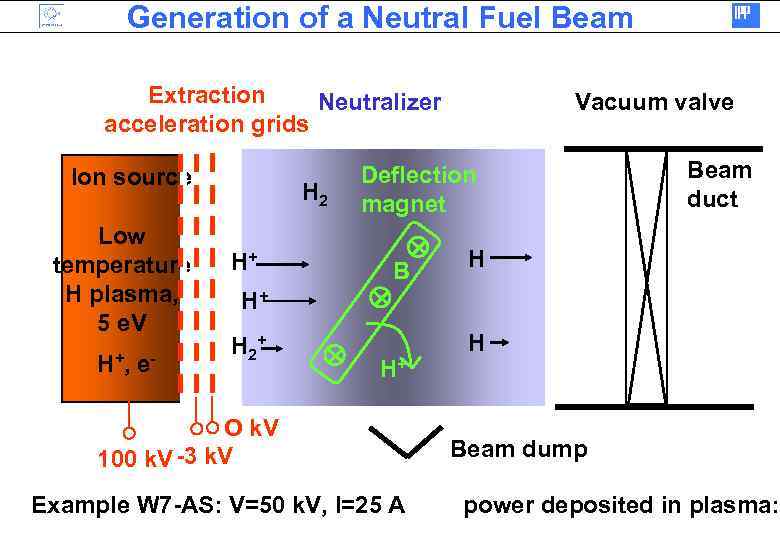Generation of a Neutral Fuel Beam Extraction Neutralizer acceleration grids Ion source Low temperature H plasma, 5 e. V H+ , e - H 2 H+ Vacuum valve Deflection magnet B Beam duct H H+ H 2+ H+ O k. V 100 k. V -3 k. V Example W 7 -AS: V=50 k. V, I=25 A H Beam dump power deposited in plasma:

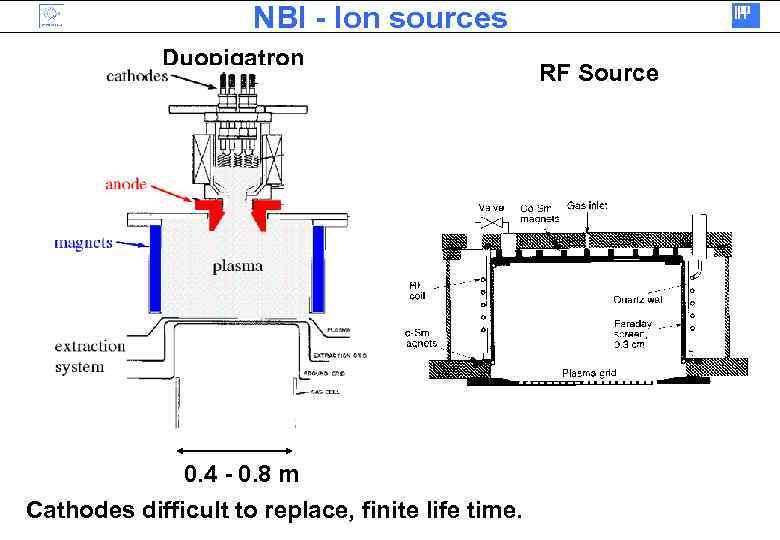NBI - Ion sources Duopigatron 0. 4 - 0. 8 m Cathodes difficult to replace, finite life time. RF Source

NBI - Extraction and steering 3 -lens system potential lines 0. 2 m H+ 85% H 2+ 12% H 3+ 3% 0. 5 m 100 k. V -3 k. V 0 k. V Typically 800 extraction holes per source. Grid system ASDEX Upgrade.

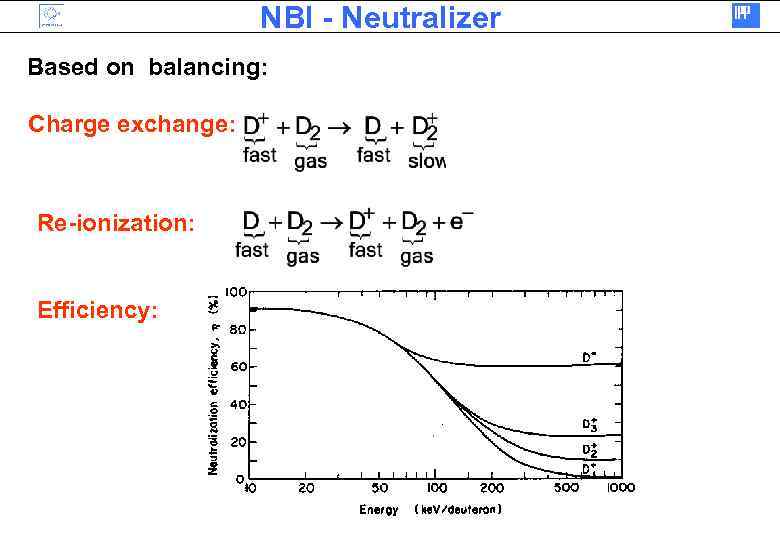NBI - Neutralizer Based on balancing: Charge exchange: Re-ionization: Efficiency:

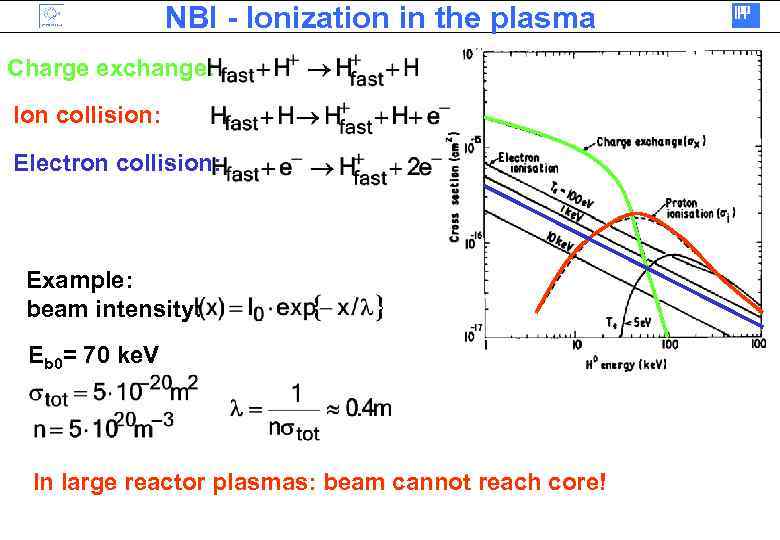NBI - Ionization in the plasma Charge exchange: Ion collision: Electron collision: Example: beam intensity: Eb 0= 70 ke. V In large reactor plasmas: beam cannot reach core!

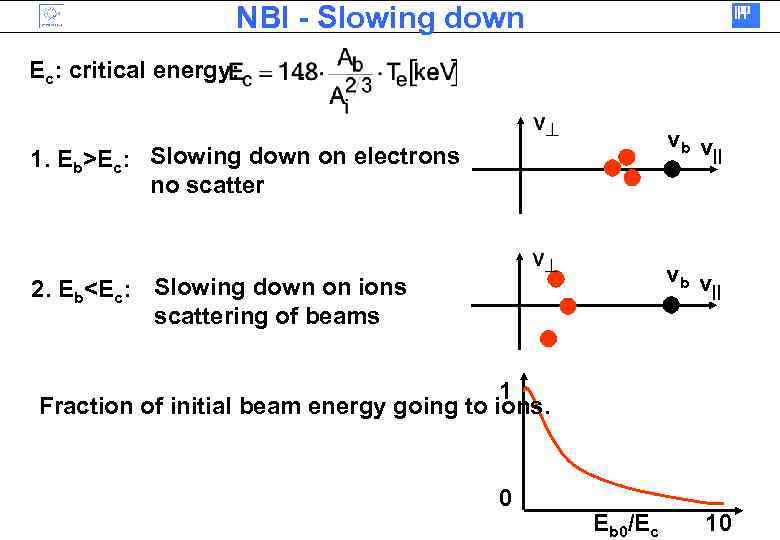NBI - Slowing down Ec: critical energy: vb v || 1. Eb>Ec: Slowing down on electrons no scatter vb v || 2. Eb

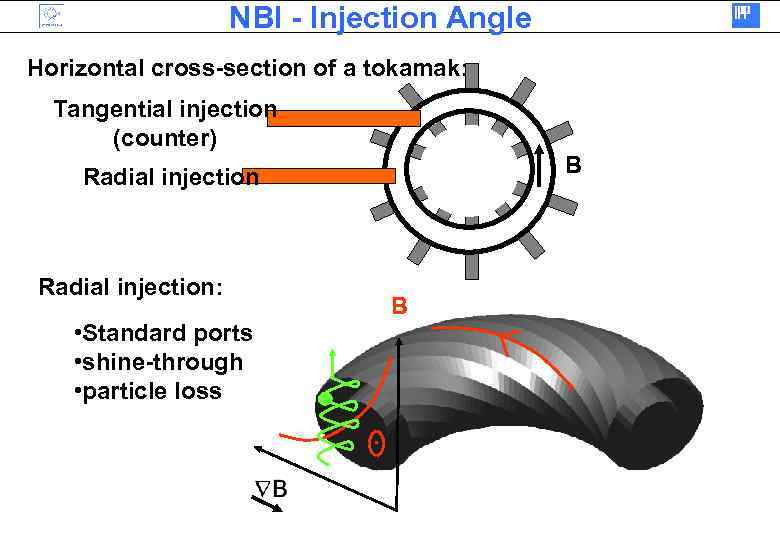NBI - Injection Angle Horizontal cross-section of a tokamak: Tangential injection (counter) B Radial injection: B • Standard ports • shine-through • particle loss.

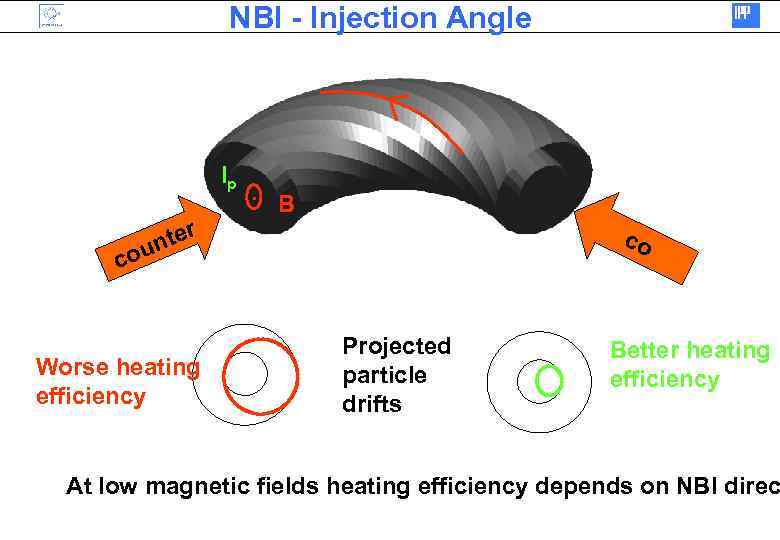NBI - Injection Angle Ip ter un . B co co Worse heating efficiency Projected particle drifts Better heating efficiency At low magnetic fields heating efficiency depends on NBI direc

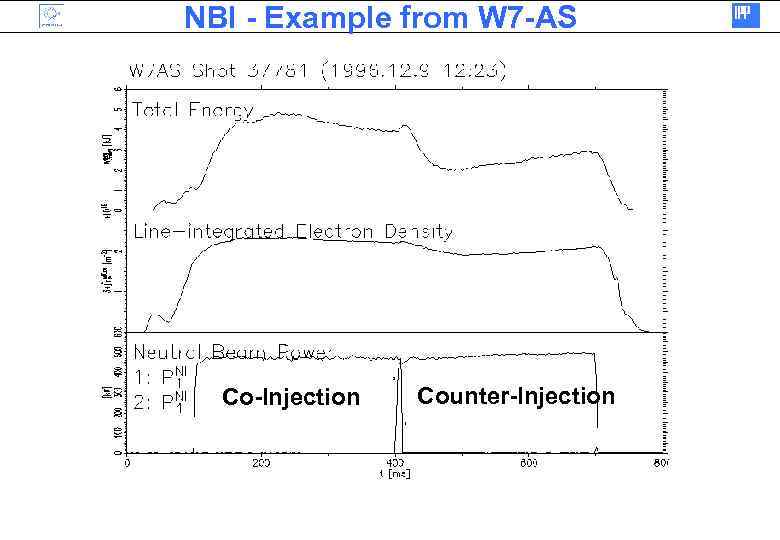NBI - Example from W 7 -AS Co-Injection Counter-Injection

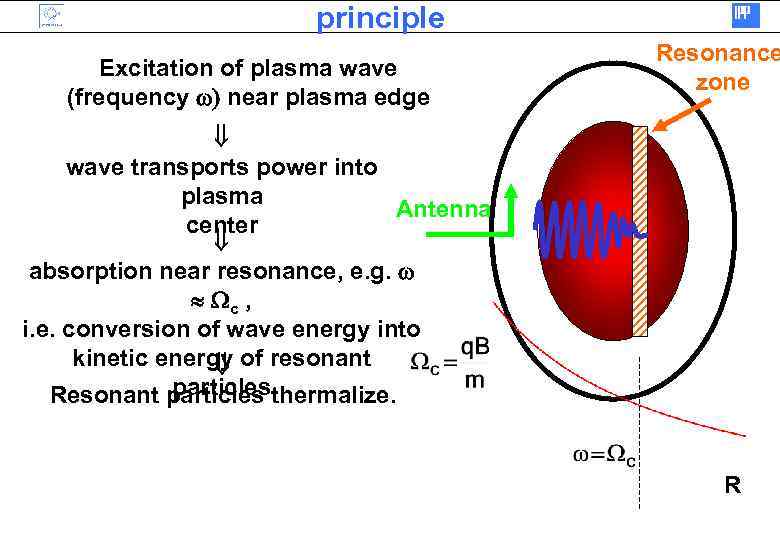principle Excitation of plasma wave (frequency ) near plasma edge Resonance zone wave transports power into plasma Antenna center absorption near resonance, e. g. c , i. e. conversion of wave energy into kinetic energy of resonant particles Resonant particles thermalize. R

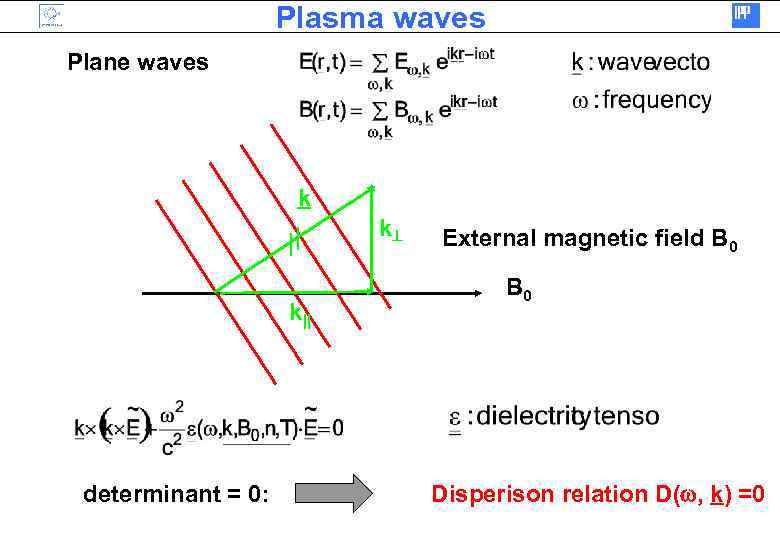Plasma waves Plane waves k k k|| determinant = 0: External magnetic field B 0 Disperison relation D( , k) =0

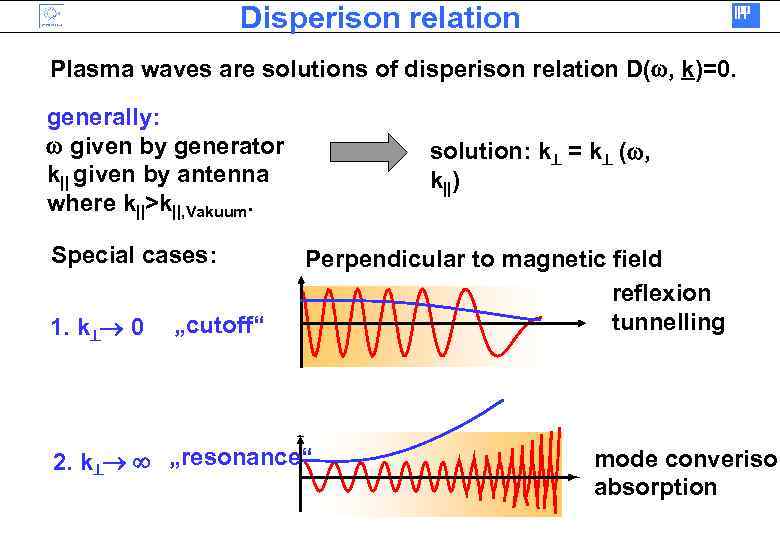Disperison relation Plasma waves are solutions of disperison relation D( , k)=0. generally: given by generator k|| given by antenna where k||>k||, Vakuum. Special cases: 1. k 0 „cutoff“ solution: k = k ( , k||) Perpendicular to magnetic field reflexion tunnelling 2. k „resonance“ mode converison absorption

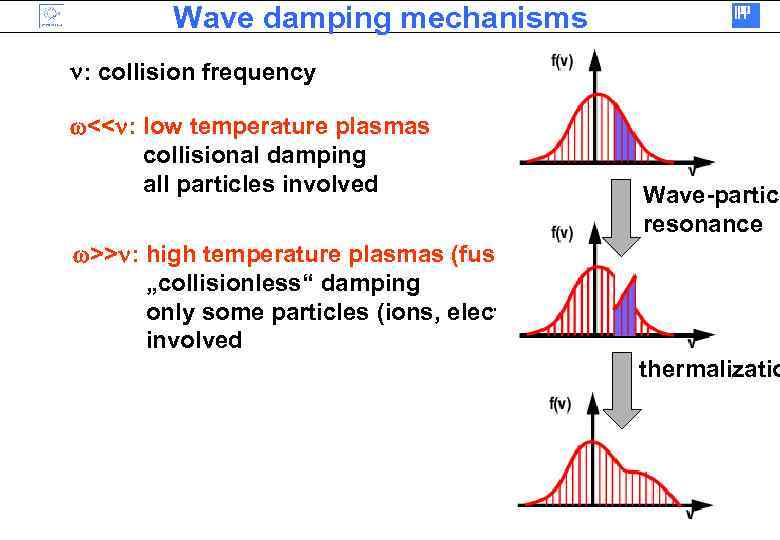Wave damping mechanisms n: collision frequency <>n: high temperature plasmas (fusion) „collisionless“ damping only some particles (ions, electrons) involved thermalizatio

Collisionless Wave Damping Mechanisms Damping on ions: Damping on electrons: electric EM wave field Ehf magnetic EM wave field Bhf Damping efficient only at finite temperature. Landau damping Ehf B k|| Bhf B k||=0 Landau cyclotron damping Ehf B k|| Transit time magnetic pumping Bhf B k||

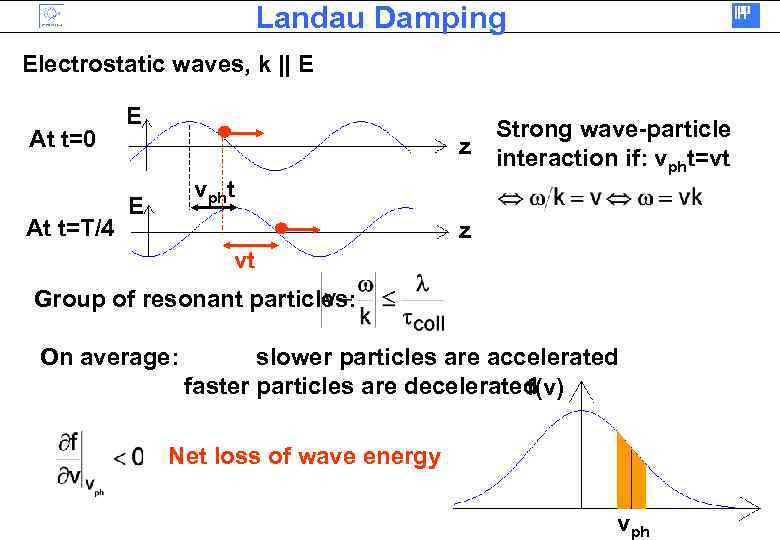Landau Damping Electrostatic waves, k || E At t=0 At t=T/4 E z vpht E Strong wave-particle interaction if: vpht=vt z vt Group of resonant particles: On average: slower particles are accelerated faster particles are decelerated f(v) Net loss of wave energy vph

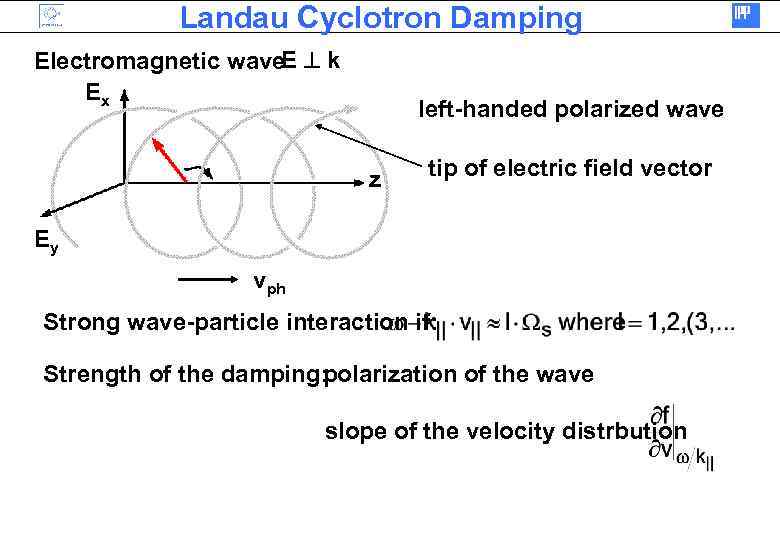Landau Cyclotron Damping Electromagnetic wave. E k Ex left-handed polarized wave z tip of electric field vector Ey vph Strong wave-particle interaction if: Strength of the damping: olarization of the wave p slope of the velocity distrbution

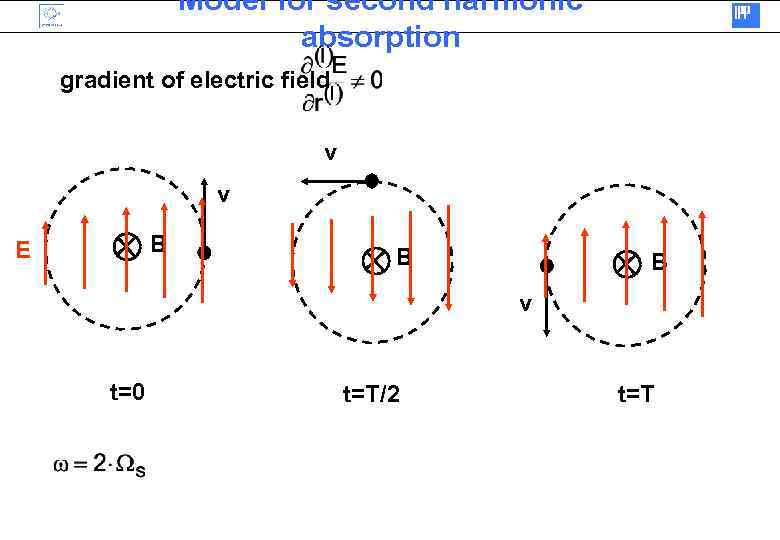Model for second harmonic absorption gradient of electric field v v B E B B v t=0 t=T/2 t=T

Transit Time Magnetic Pumping Magnetic moment approximately conserved: m B+Bhf Force on magnetic moment: Similar to Landau damping with substitution:

Please, stay tune

Frequencies with good absorption Landau Cyclotron Resonance generally Then good absorption where Electrons: Hydrogen: 28 GHz / B[T] 15 MHz / B [T] Electron Cyclotron Resonan Ion Cyclotron Resonance H Landau Resonance Lower Hybrid Heating LH Landau Resonance and Magn. Pumping also contribute to ICRH

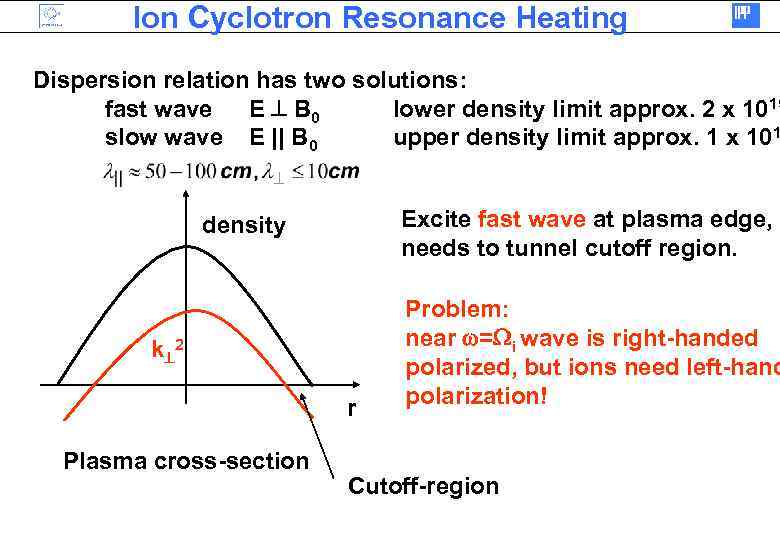Ion Cyclotron Resonance Heating Dispersion relation has two solutions: fast wave E B 0 lower density limit approx. 2 x 1019 slow wave E || B 0 upper density limit approx. 1 x 101 Excite fast wave at plasma edge, needs to tunnel cutoff region. density k 2 r Plasma cross-section Problem: near = i wave is right-handed polarized, but ions need left-hand polarization! Cutoff-region

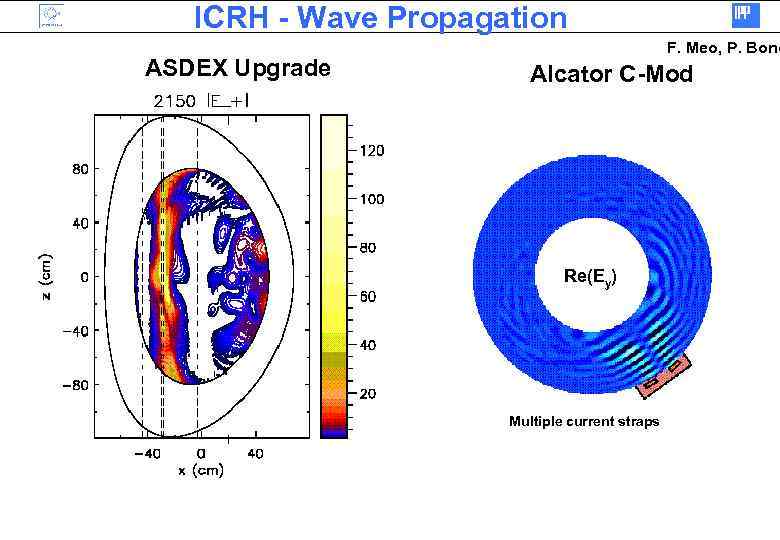ICRH - Wave Propagation ASDEX Upgrade F. Meo, P. Bono Alcator C-Mod Re(Ey) Multiple current straps

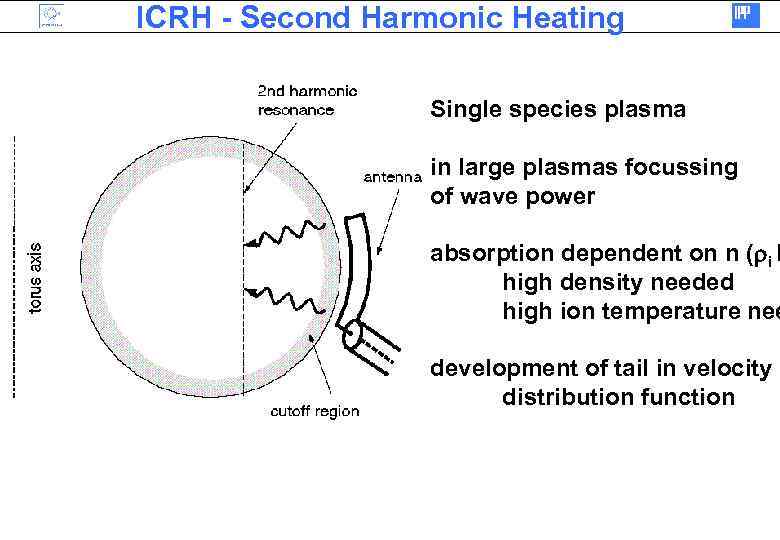ICRH - Second Harmonic Heating Single species plasma in large plasmas focussing of wave power absorption dependent on n (ri k high density needed high ion temperature nee development of tail in velocity distribution function

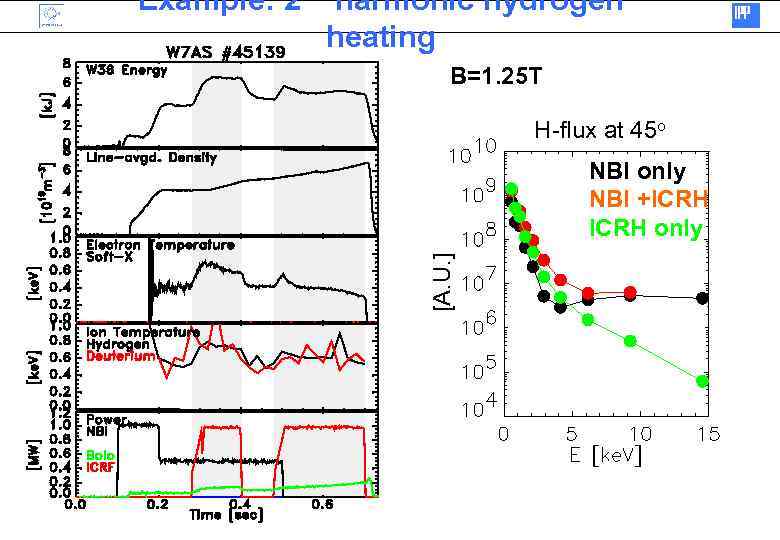Example: 2 nd harmonic hydrogen heating B=1. 25 T H-flux at 45 o [A. U. ] NBI only NBI +ICRH only

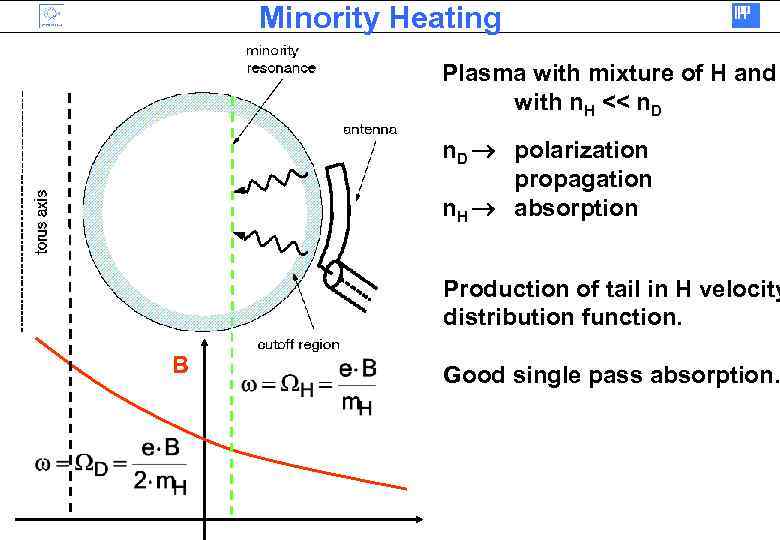Minority Heating Plasma with mixture of H and with n. H << n. D polarization propagation n. H absorption Production of tail in H velocity distribution function. B Good single pass absorption.

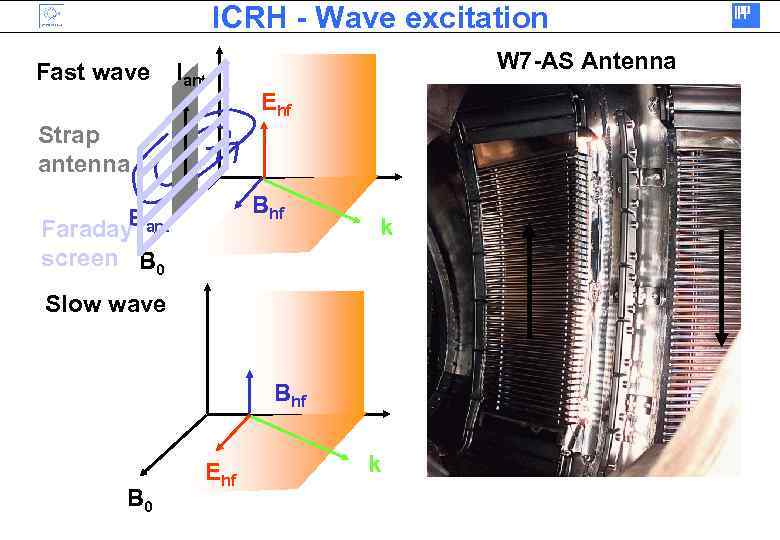ICRH - Wave excitation Fast wave Iant W 7 -AS Antenna Ehf Strap antenna Bhf B Faraday ant screen B 0 k Slow wave Bhf B 0 Ehf k

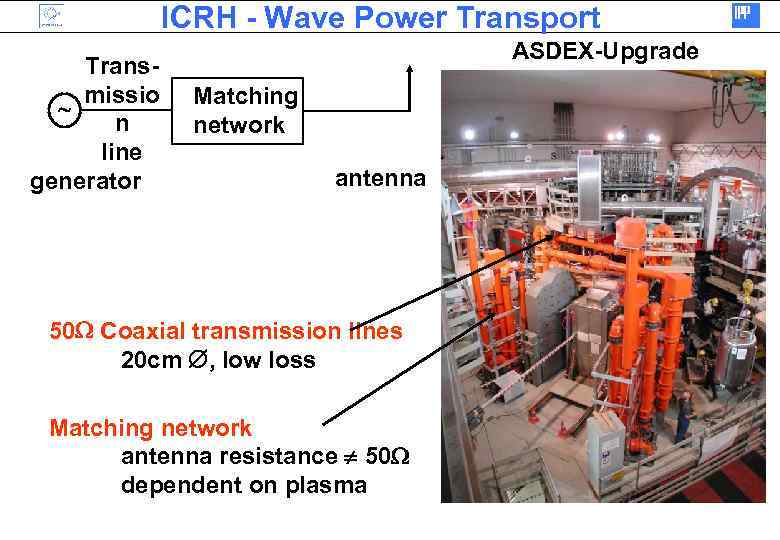ICRH - Wave Power Transport Transmissio n line generator ASDEX-Upgrade Matching network antenna 50 Coaxial transmission lines 20 cm , low loss Matching network antenna resistance 50 dependent on plasma

ICRF Technology - Generator 4 amplifier chain final stage: tetrode with 2 MW / 10 sec tunable between 30 and 110 MHz efficiency 60% tetrode

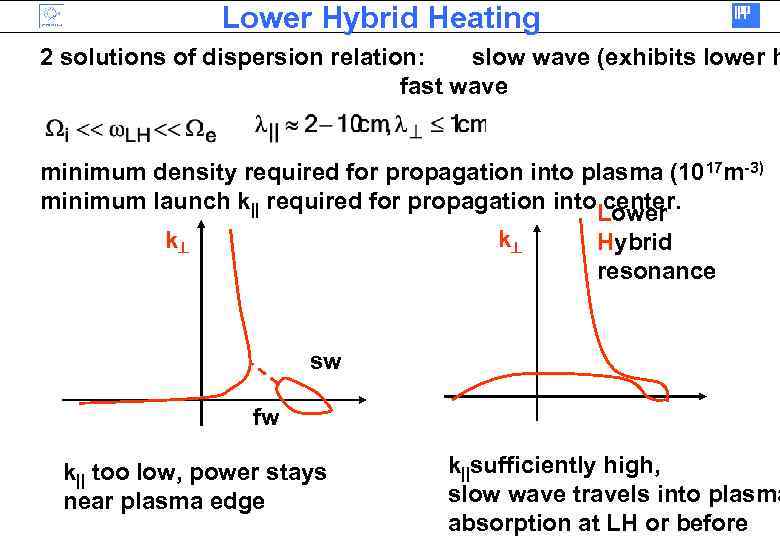Lower Hybrid Heating 2 solutions of dispersion relation: slow wave (exhibits lower h fast wave minimum density required for propagation into plasma (1017 m-3) minimum launch k|| required for propagation into center. Lower k k Hybrid resonance sw fw k|| too low, power stays near plasma edge k||sufficiently high, slow wave travels into plasma absorption at LH or before

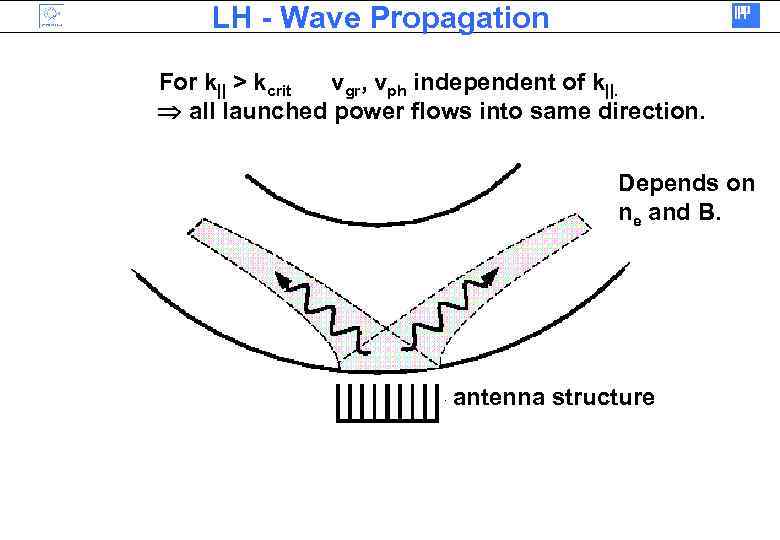LH - Wave Propagation For k|| > kcrit vgr, vph independent of k||. all launched power flows into same direction. Depends on ne and B. antenna structure

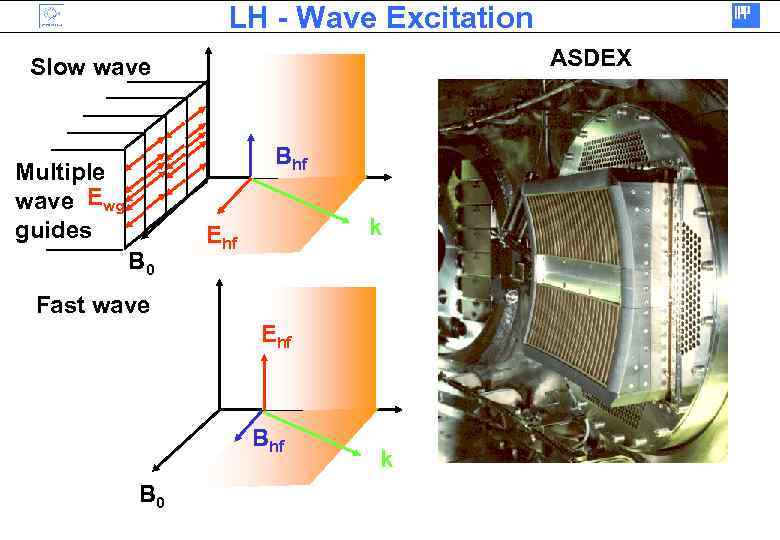LH - Wave Excitation ASDEX Slow wave Bhf Multiple wave Ewg guides B 0 k Ehf Fast wave Ehf B 0 k

Wave power transport klystron waveguide grill

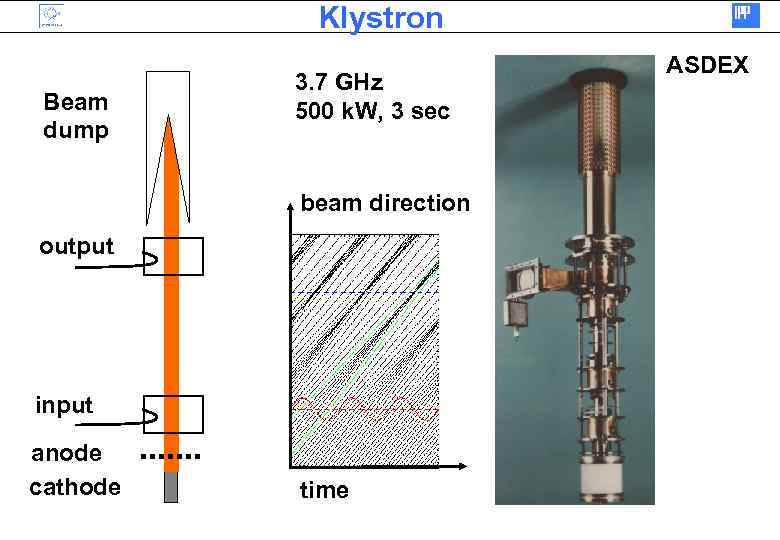Klystron Beam dump 3. 7 GHz 500 k. W, 3 sec beam direction output input anode cathode time ASDEX

Electron Cyclotron Resonance Heating Dispersion relation has two solutions for perpendicular propagati ordinary (O)-mode E || B 0 extraordinary (X)-mode E B 0 No low density cut-off, but high density cutoff. Ions can be assumed stationary, but relativistic electron mass ha be included.

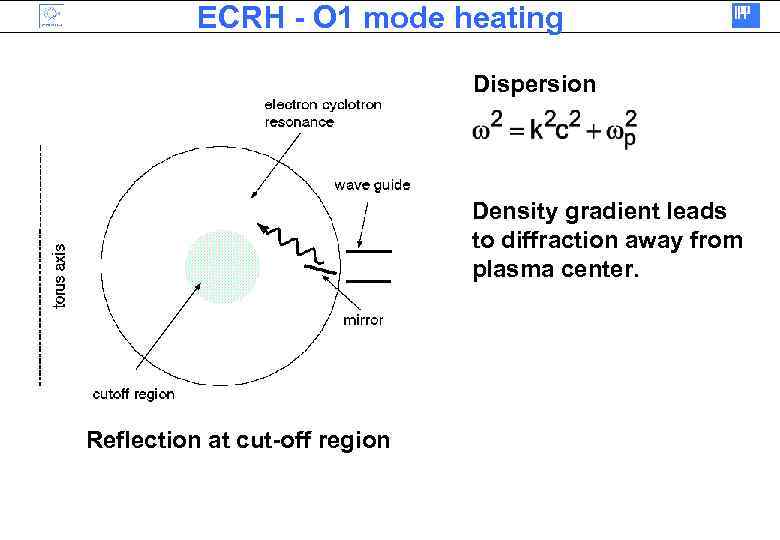ECRH - O 1 mode heating Dispersion Density gradient leads to diffraction away from plasma center. Reflection at cut-off region

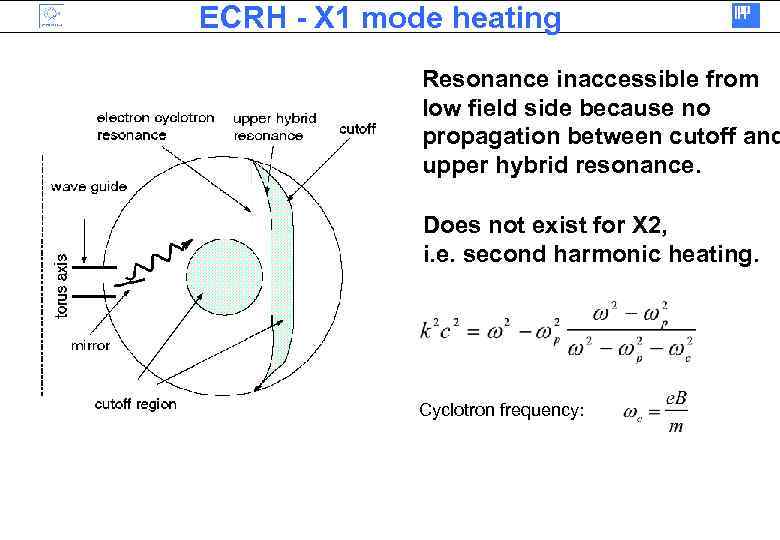ECRH - X 1 mode heating Resonance inaccessible from low field side because no propagation between cutoff and upper hybrid resonance. Does not exist for X 2, i. e. second harmonic heating. Cyclotron frequency:

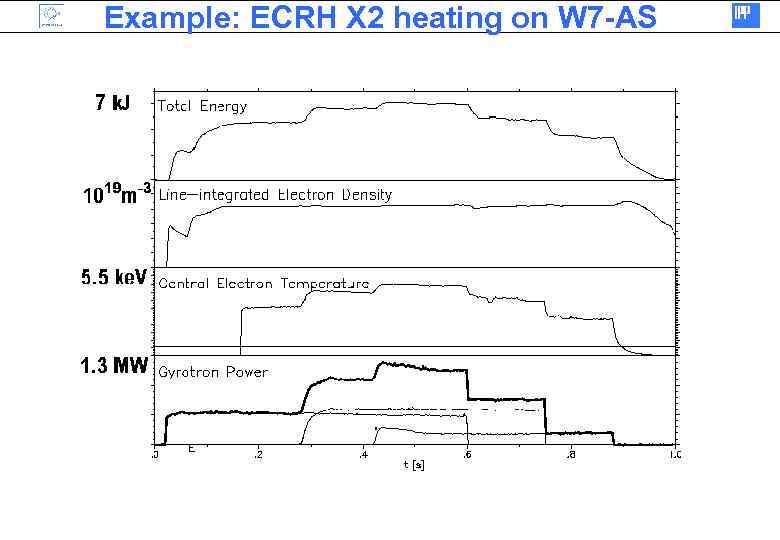Example: ECRH X 2 heating on W 7 -AS

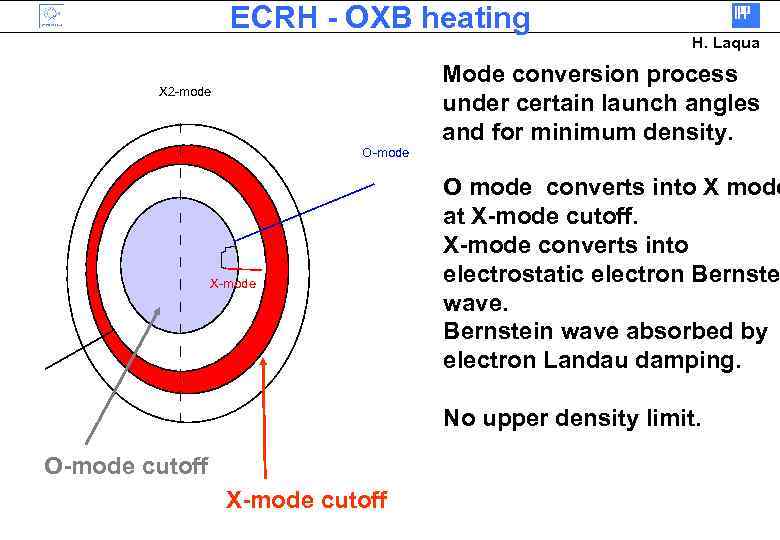ECRH - OXB heating H. Laqua Mode conversion process under certain launch angles and for minimum density. X 2 -mode O-mode X-mode O mode converts into X mode at X-mode cutoff. X-mode converts into electrostatic electron Bernste wave. Bernstein wave absorbed by electron Landau damping. No upper density limit. O-mode cutoff X-mode cutoff

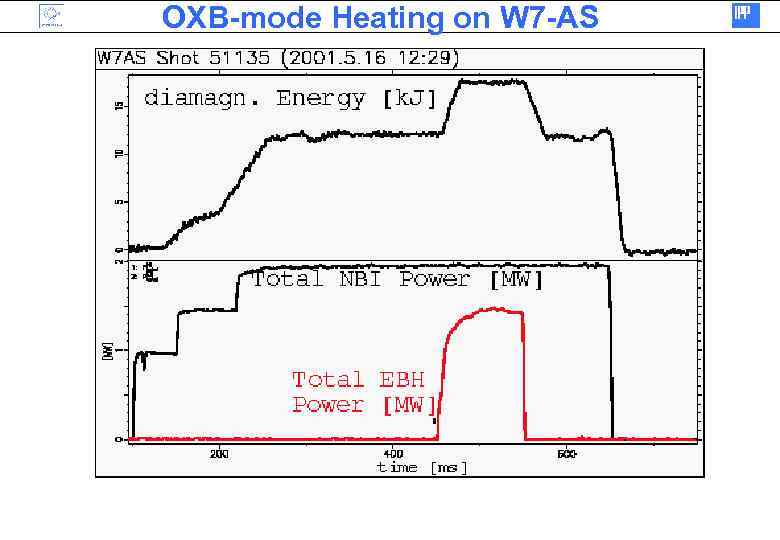OXB-mode Heating on W 7 -AS

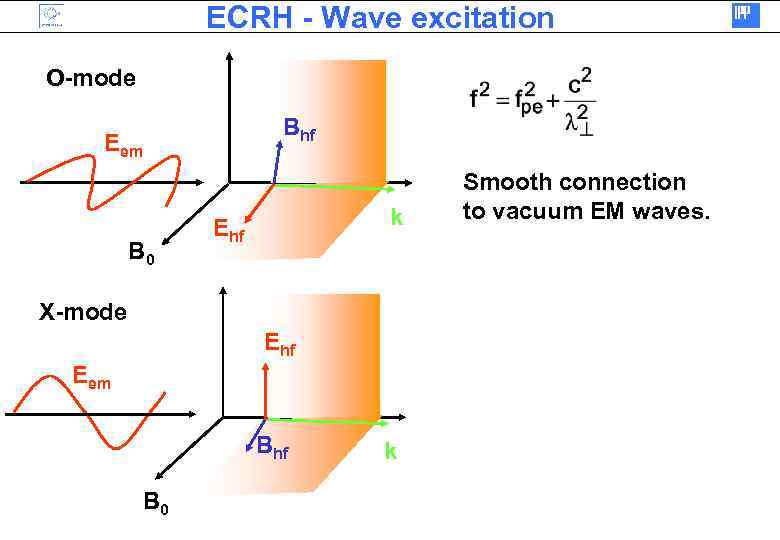ECRH - Wave excitation O-mode Bhf Eem B 0 k Ehf X-mode Ehf Eem Bhf B 0 k Smooth connection to vacuum EM waves.

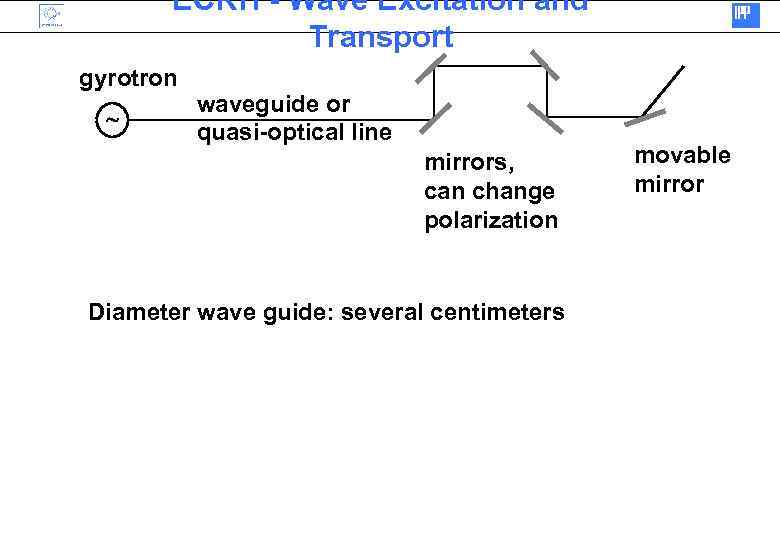ECRH - Wave Excitation and Transport gyrotron waveguide or quasi-optical line mirrors, can change polarization Diameter wave guide: several centimeters movable mirror

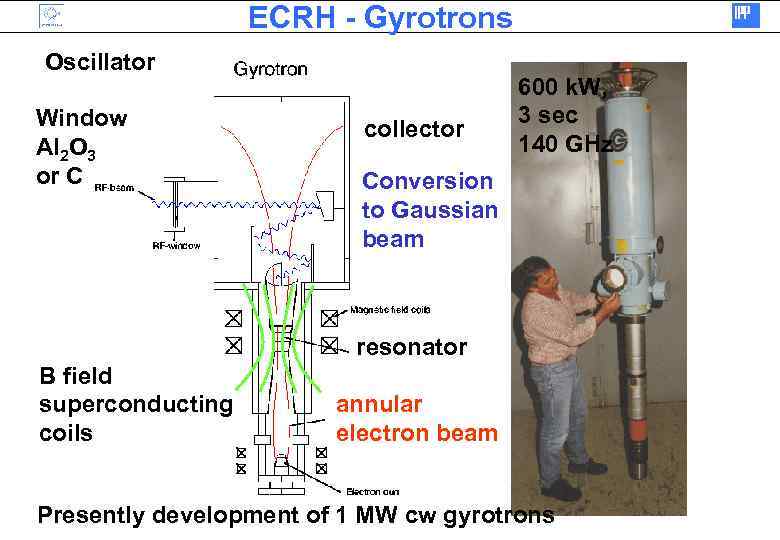ECRH - Gyrotrons Oscillator Window Al 2 O 3 or C collector 600 k. W, 3 sec 140 GHz Conversion to Gaussian beam resonator B field superconducting coils annular electron beam Presently development of 1 MW cw gyrotrons

a-Particle Heating D-T fusion reaction: Heating power density: where peaked heating profile a-particles need to be well confined through large plasma currents in tokamaks optimized stellarator fields Loss mechanisms: field ripples MHD events

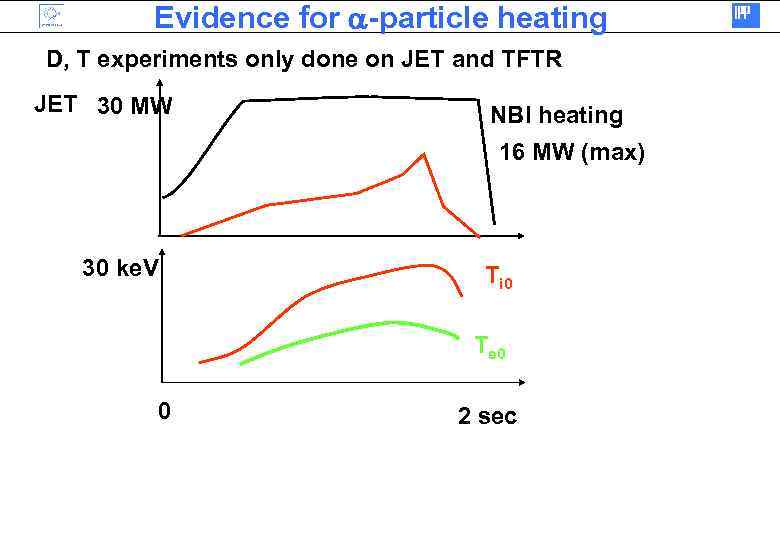Evidence for a-particle heating D, T experiments only done on JET and TFTR JET 30 MW NBI heating 16 MW (max) 30 ke. V Ti 0 Te 0 0 2 sec

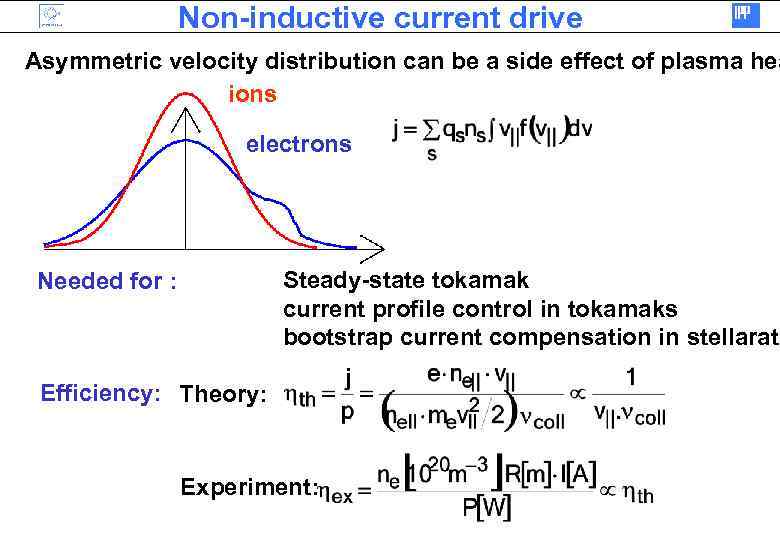Non-inductive current drive Asymmetric velocity distribution can be a side effect of plasma hea ions electrons Steady-state tokamak current profile control in tokamaks bootstrap current compensation in stellarato Needed for : Efficiency: Theory: Experiment:

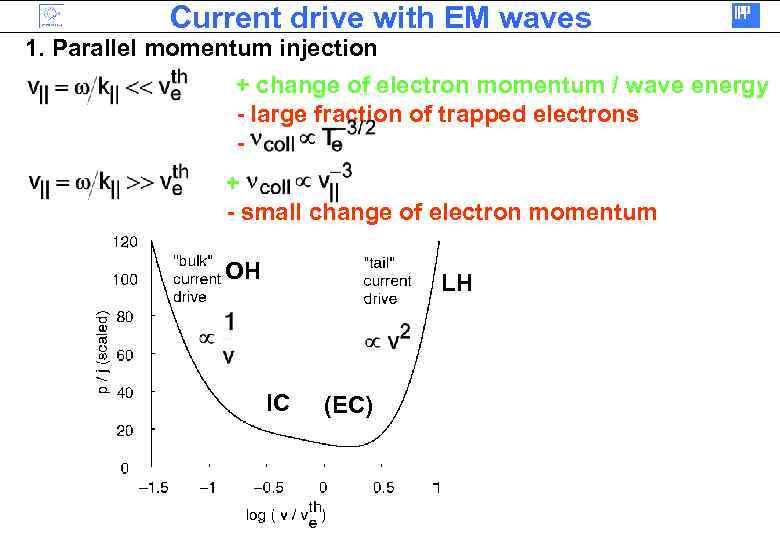Current drive with EM waves 1. Parallel momentum injection + change of electron momentum / wave energy - large fraction of trapped electrons + - small change of electron momentum OH LH IC (EC)

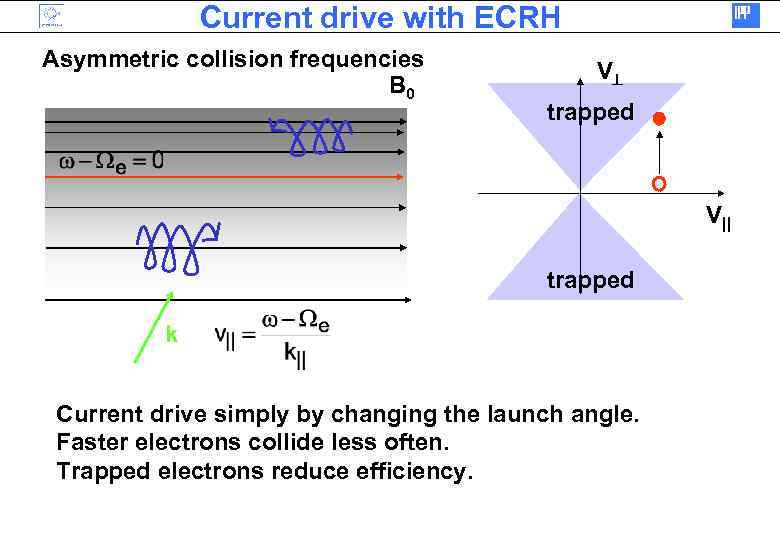Current drive with ECRH Asymmetric collision frequencies B 0 V trapped V|| trapped k Current drive simply by changing the launch angle. Faster electrons collide less often. Trapped electrons reduce efficiency.

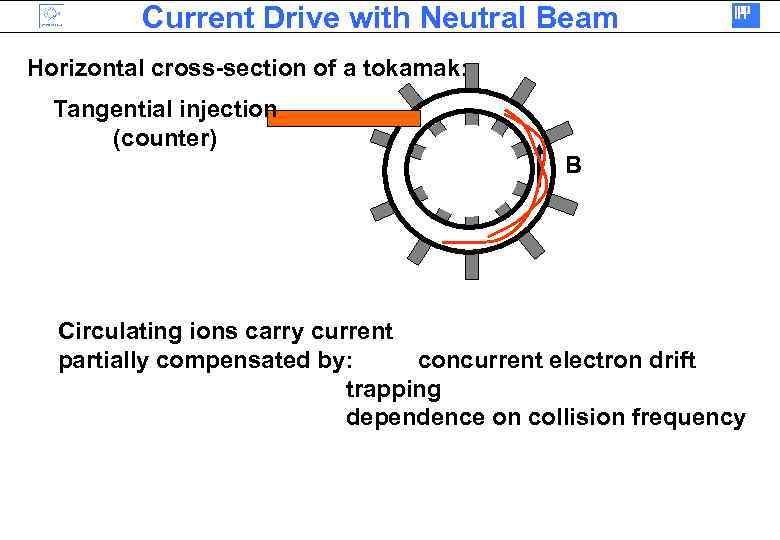Current Drive with Neutral Beam Horizontal cross-section of a tokamak: Tangential injection (counter) B Circulating ions carry current partially compensated by: concurrent electron drift trapping dependence on collision frequency

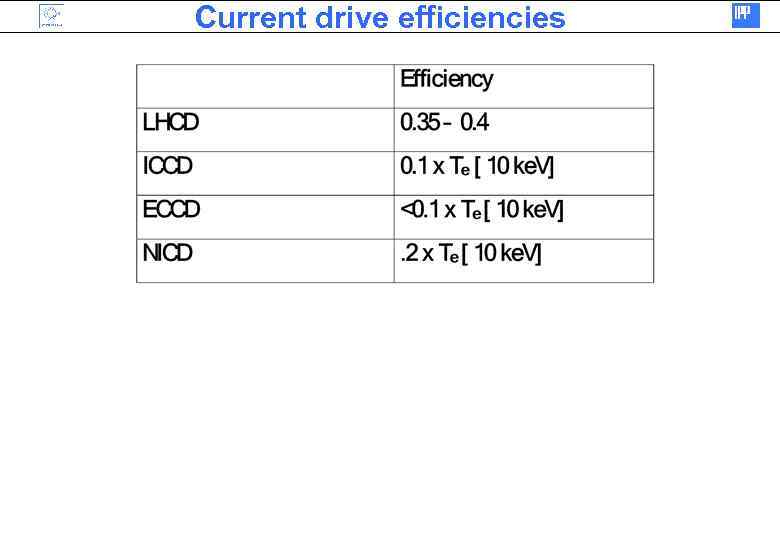Current drive efficiencies

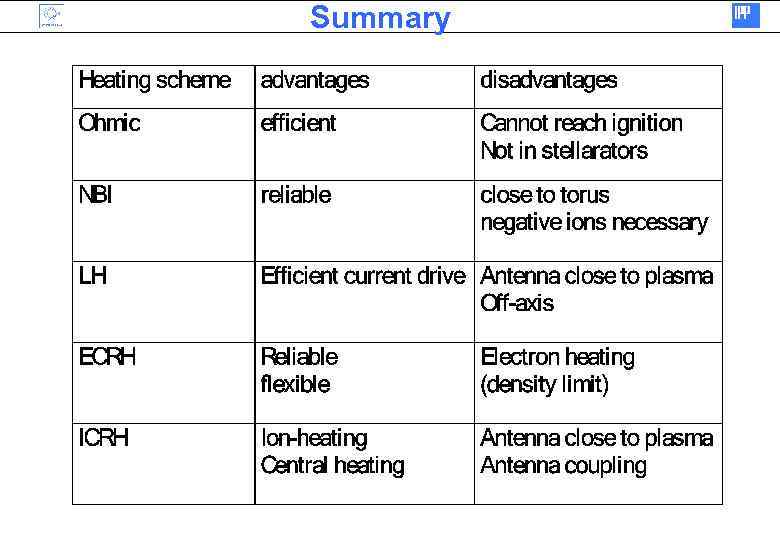Summary