Планирование эксперимента Полный факторный эксперимент 9 5

Планирование эксперимента Полный факторный эксперимент

(9. 5) (9. 6)

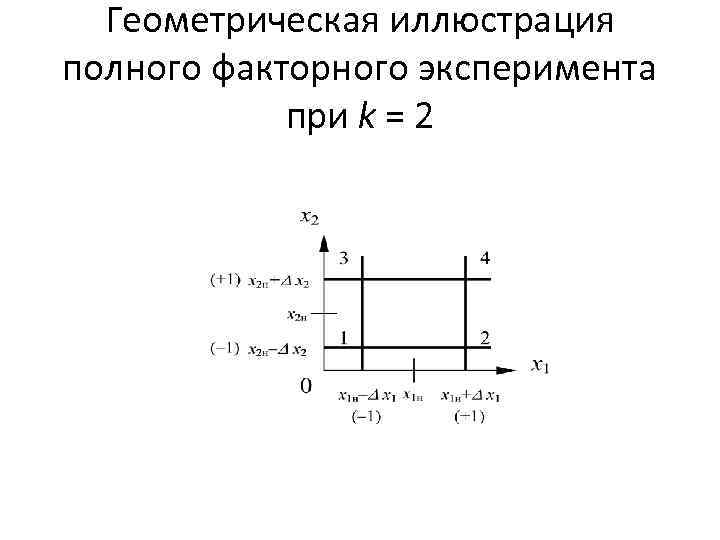Геометрическая иллюстрация полного факторного эксперимента при k = 2

Матрица планировании ПФЭ № опыта x 1 x 2 y 1 – 1 y 1 2 +1 – 1 y 2 3 – 1 +1 y 3 4 +1 +1 y 4

(9. 7) (9. 8) где N 0 – число параллельных опытов; среднее значение параллельных опытов fy – число степеней свободы – величина, показывающая, какое число связей независимых наблюдений осталось не задействовано (fy = N 0 – 1, так как одна связь использована при нахождении

Определяем критерий Стьюдента для каждого коэффициента (9. 9) Для вычисления F-критерия Фишера находим дисперсию адекватности S 2 ад (9. 10) где yiр – расчетные значения, получаемые по уравнению (9. 3); fад = (N – d) – число степеней свободы дисперсии адекватности; N – количество опытов; d – число значимых коэффициентов регрессии.

Затем определяем расчетное значение F-критерия Фишера (9. 11) (9. 12) (9. 13)

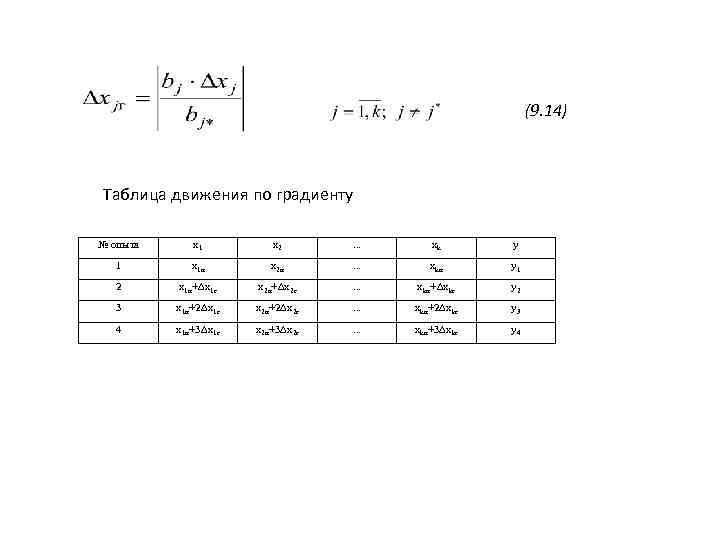(9. 14) Таблица движения по градиенту № опыта x 1 x 2 . . . xk y 1 x 1 н x 2 н . . . xkн y 1 2 x 1 н+ x 1 г x 2 н+ x 2 г . . . xkн+ xkг y 2 3 x 1 н+2 x 1 г x 2 н+2 x 2 г . . . xkн+2 xkг y 3 4 x 1 н+3 x 1 г x 2 н+3 x 2 г . . . xkн+3 xkг y 4

Дробный факторный эксперимент

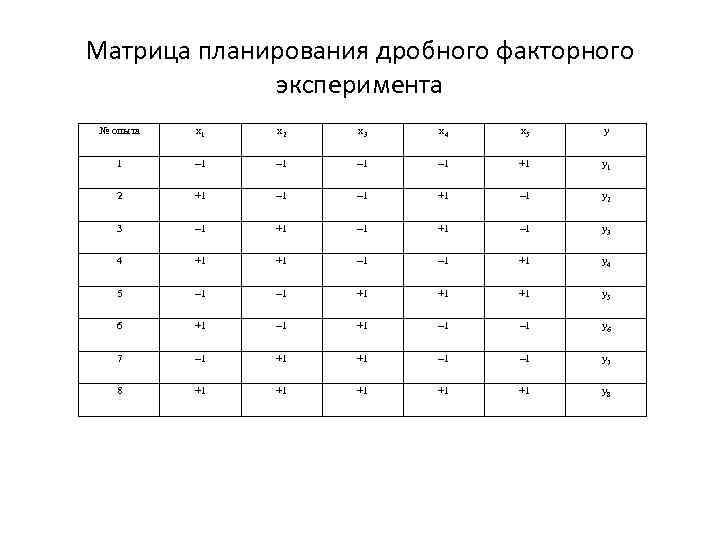Матрица планирования дробного факторного эксперимента № опыта x 1 x 2 x 3 x 4 x 5 y 1 – 1 – 1 +1 y 1 2 +1 – 1 y 2 3 – 1 +1 – 1 y 3 4 +1 +1 – 1 +1 y 4 5 – 1 +1 +1 +1 y 5 6 +1 – 1 – 1 y 6 7 – 1 +1 +1 – 1 y 7 8 +1 +1 +1 y 8

Пример оптимизации химического реактора Рассмотрим применение метода Бокса-Вильсона на примере оптимизации химического реактора. Допустим, что производительность химического реактора зависит от трех факторов: температуры процесса x 1 (0 С), объемной скорости потока x 2 (м 3/час) и концентрации катализатора x 3 (моль/л). Начальные значения факторов: x 1 н = 150; x 2 н = 20; x 3 н = 0, 3; интервалы варьирования: x 1 = 20; x 2 = 4; x 3 = 0, 05.

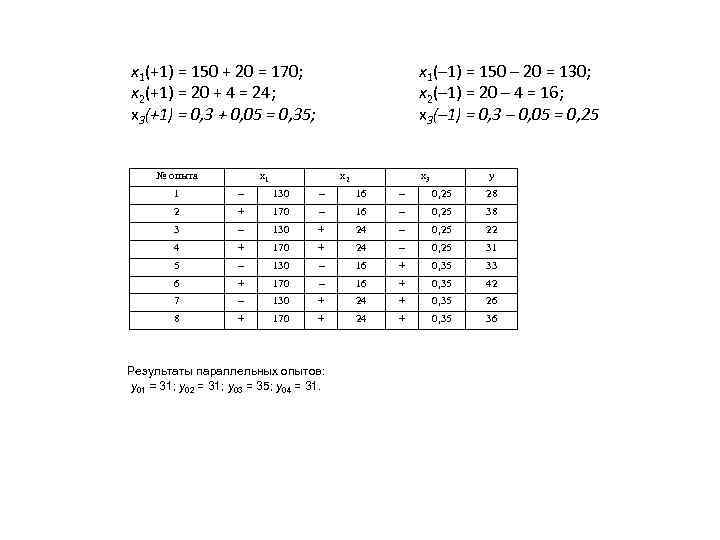x 1(+1) = 150 + 20 = 170; x 2(+1) = 20 + 4 = 24; x 3(+1) = 0, 3 + 0, 05 = 0, 35; № опыта x 1(– 1) = 150 – 20 = 130; x 2(– 1) = 20 – 4 = 16; x 3(– 1) = 0, 3 – 0, 05 = 0, 25 x 1 x 2 x 3 y 1 – 130 – 16 – 0, 25 28 2 + 170 – 16 – 0, 25 38 3 – 130 + 24 – 0, 25 22 4 + 170 + 24 – 0, 25 31 5 – 130 – 16 + 0, 35 33 6 + 170 – 16 + 0, 35 42 7 – 130 + 24 + 0, 35 26 8 + 170 + 24 + 0, 35 36 Результаты параллельных опытов: y 01 = 31; y 02 = 31; y 03 = 35; y 04 = 31.

y = 32 + 4, 75 x 1 – 3, 25 x 2 y 1 = 32 + 4, 75 (– 1) – 3, 25 (– 1) = 30, 5, y 2 = 32 + 4, 75 (+1) – 3, 25 (– 1) = 40, y 3 = 32 + 4, 75 (– 1) – 3, 25 (+1) = 24, y 4 = 32 + 4, 75 (+1) – 3, 25 (+1) = 33, 5,

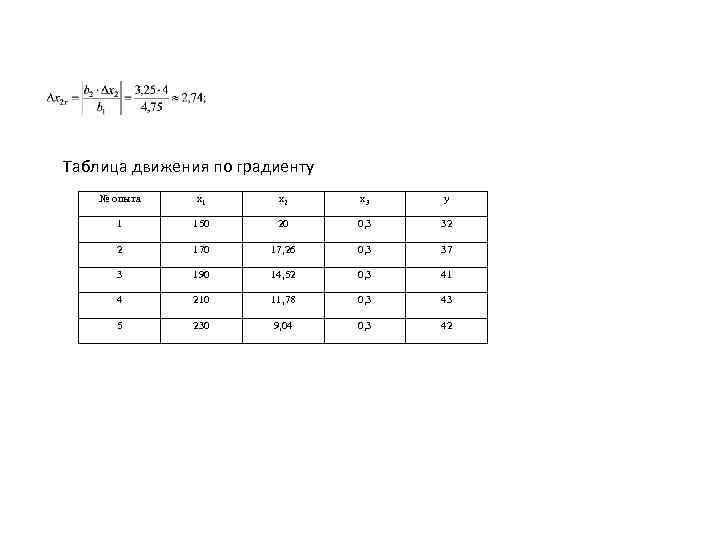Таблица движения по градиенту № опыта x 1 x 2 x 3 y 1 150 20 0, 3 32 2 170 17, 26 0, 3 37 3 190 14, 52 0, 3 41 4 210 11, 78 0, 3 43 5 230 9, 04 0, 3 42

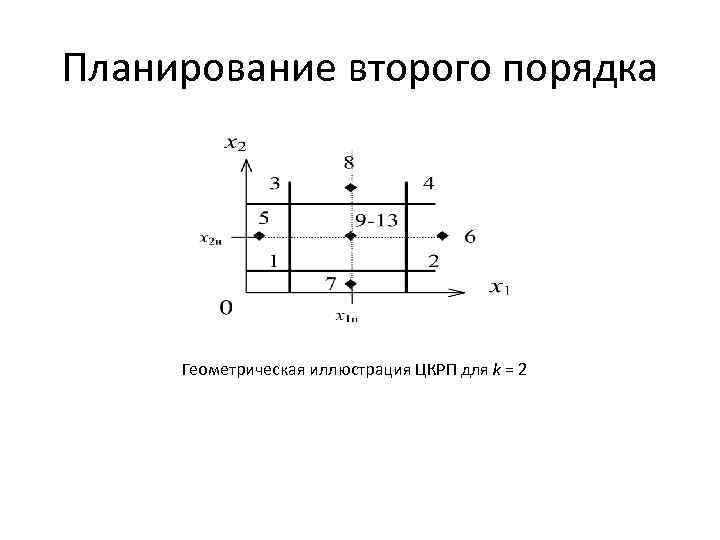Планирование второго порядка Геометрическая иллюстрация ЦКРП для k = 2

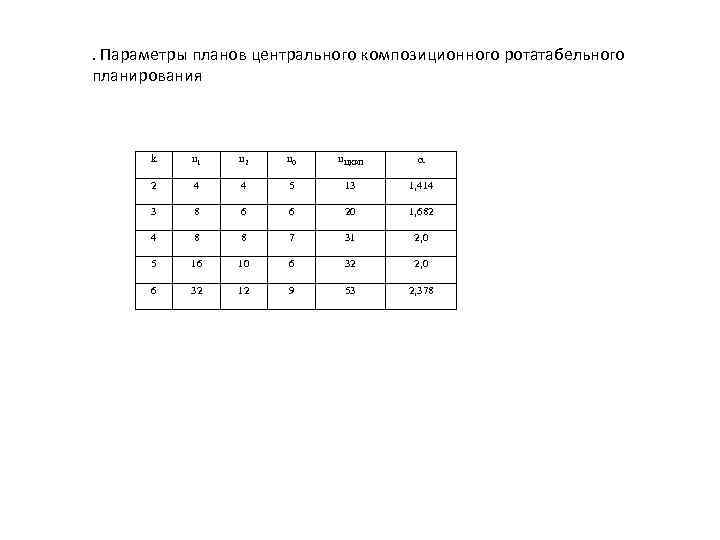. Параметры планов центрального композиционного ротатабельного планирования k n 1 n 2 n 0 n. ЦКРП 2 4 4 5 13 1, 414 3 8 6 6 20 1, 682 4 8 8 7 31 2, 0 5 16 10 6 32 2, 0 6 32 12 9 53 2, 378

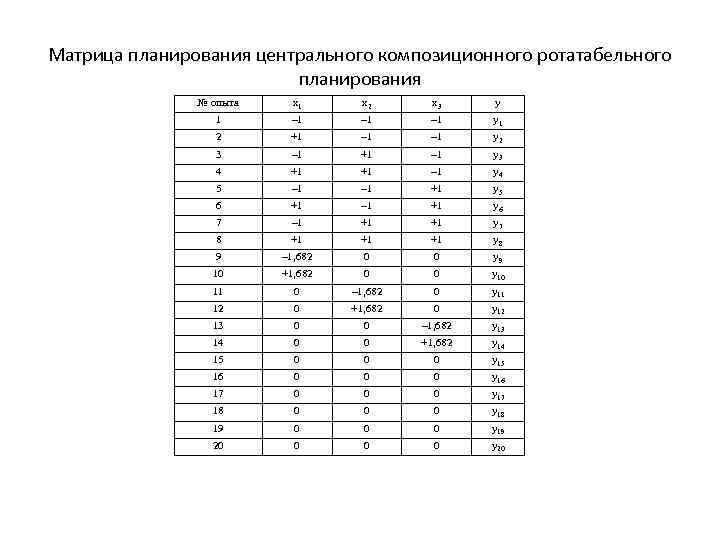Матрица планирования центрального композиционного ротатабельного планирования № опыта x 1 x 2 x 3 y 1 – 1 – 1 y 1 2 +1 – 1 y 2 3 – 1 +1 – 1 y 3 4 +1 +1 – 1 y 4 5 – 1 +1 y 5 6 +1 – 1 +1 y 6 7 – 1 +1 +1 y 7 8 +1 +1 +1 y 8 9 – 1, 682 0 0 y 9 10 +1, 682 0 0 y 10 11 0 – 1, 682 0 y 11 12 0 +1, 682 0 y 12 13 0 0 – 1, 682 y 13 14 0 0 +1, 682 y 14 15 0 0 0 y 15 16 0 0 0 y 16 17 0 0 0 y 17 18 0 0 0 y 18 19 0 0 0 y 19 20 0 y 20

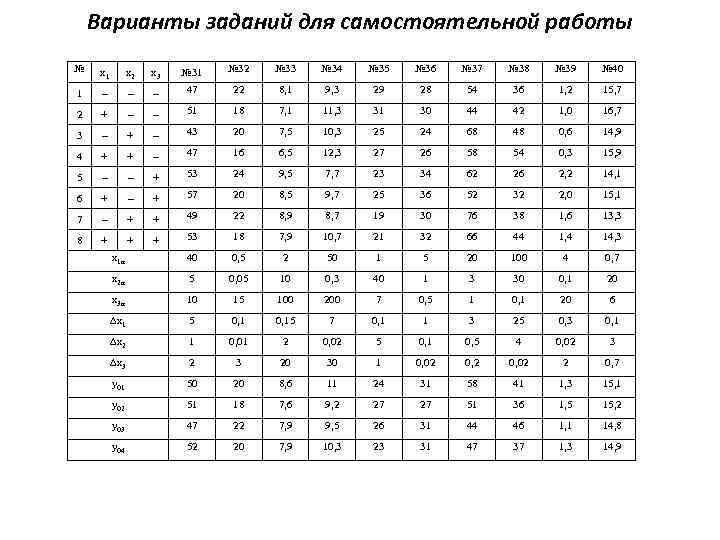Варианты заданий для самостоятельной работы № x 1 x 2 x 3 № 31 № 32 № 33 № 34 № 35 № 36 № 37 № 38 № 39 № 40 1 – – – 47 22 8, 1 9, 3 29 28 54 36 1, 2 15, 7 2 + – – 51 18 7, 1 11, 3 31 30 44 42 1, 0 16, 7 3 – + – 43 20 7, 5 10, 3 25 24 68 48 0, 6 14, 9 4 + + – 47 16 6, 5 12, 3 27 26 58 54 0, 3 15, 9 5 – – + 53 24 9, 5 7, 7 23 34 62 26 2, 2 14, 1 6 + – + 57 20 8, 5 9, 7 25 36 52 32 2, 0 15, 1 7 – + + 49 22 8, 9 8, 7 19 30 76 38 1, 6 13, 3 8 + + + 53 18 7, 9 10, 7 21 32 66 44 1, 4 14, 3 x 1 н 40 0, 5 2 50 1 5 20 100 4 0, 7 x 2 н 5 0, 05 10 0, 3 40 1 3 30 0, 1 20 x 3 н 10 15 100 200 7 0, 5 1 0, 1 20 6 x 1 5 0, 15 7 0, 1 1 3 25 0, 3 0, 1 x 2 1 0, 01 2 0, 02 5 0, 1 0, 5 4 0, 02 3 x 3 20 30 1 0, 02 2 0, 7 y 01 50 20 8, 6 11 24 31 58 41 1, 3 15, 1 y 02 51 18 7, 6 9, 2 27 27 51 36 1, 5 15, 2 y 03 47 22 7, 9 9, 5 26 31 44 46 1, 1 14, 8 y 04 52 20 7, 9 10, 3 23 31 47 37 1, 3 14, 9