Планир_эксперим.pptx
- Количество слайдов: 40

ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА И ОБРАБОТКА ЕГО РЕЗУЛЬТАТОВ 1. 2. 3. 4. 5. 6. 7. 8. Введение в планирование эксперимента Характеристика и достоинства метода Область применения планирование эксперимента Сущность и основные определения метода Основные принципы пла нирования ксперимента э Цель и этапы планирования эксперимента Обработка результатов и моделирование процесса Анализ результатов

Введение в планирование эксперимента Мысль о том, что эксперимент можно планировать, восходит к глубокой древности. Но только в начале ХХ века, когда люди придумали статистические методы планирование эксперимента стало возможным. Английский статистик Рональд Фишер (конец двадцатых годов), впервые показал целесообразность одновременного варьирования всеми факторами в противовес широко распространенному однофакторному эксперименту.

Введение в планирование эксперимента В начале пятидесятых годов появилось новое направление в планировании эксперимента, связанное с оптимизацией процессов, планирование экстремального эксперимента. Первая работа в этой области была опубликована в 1951 г. Боксом и Уилсоном в Англии. Экспериментатору предлагается ставить последовательные небольшие серии опытов, в каждой из которых одновременно варьируются по определенным правилам все факторы. Серии организуются таким образом, чтобы после математической обработки предыдущей можно было выбрать условия проведения (т. е. спланировать) следующую серию. Так последовательно, шаг за шагом, достигается область оптимума.

Достоинства метода Это совсем молодая область. Она бурно развивается и вызывает все больший интерес у исследователей. Достоинства метода: • позволяет сократить число опытов, • найти оптимум, • получить количественные оценки влияния факторов, • определить ошибки – делают его крайне привлекательным. Применение планирования эксперимента делает поведение экспериментатора целенаправленным и организованным, существенно способствует повышению производительности его труда и надежности полученных результатов.

Область применения Задачи, для решения которых может использоваться планирование эксперимента: • Поиск оптимальных условий, • построение интерполяционных формул, • выбор существенных факторов, • оценка и уточнение констант теоретических моделей (например, кинетических), • выбор наиболее приемлемых из некоторого множества гипотез о механизме явлений. Можно сказать, что там, где есть эксперимент, имеет место и наука о его проведении планирование эксперимента.

Основные определения Данный раздел науки, имеет свою терминологию. Большинство научных исследований связано с экспериментом. Он проводится в лабораториях, на производстве, на опытных полях и участках, в клиниках и т. д. Эксперимент может быть физическим, психологическим или модельным. Он может непосредственно проводиться на объекте или на его модели. Модель обычно отличается от объекта масштабом, а иногда природой. Если модель достаточно описывает объект, то эксперимент на объекте может быть заменен экспериментом на модели.

Основные определения Насколько эффективно используется эксперимент? Отмечают, что научные исследования организуются и проводятся настолько хаотично, что их коэффициент полезного действия может быть оценен величиной порядка 2%. Для того чтобы повысить эффективность исследований, требуется нечто совершенно новое. Одним из возможных путей является применение математических методов, построение математической теории планирования эксперимента.

Сущность планирования эксперимента Планирование эксперимента это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. При этом существенно следующее: • стремление к минимизации общего числа опытов; • одновременное варьирование всеми переменными, определяющими процесс, по специальным правилам алгоритмам; • использование математического аппарата, формализующего многие действия экспериментатора; • выбор четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов.

Эксперимент и задачи оптимизации Эксперимент, который ставится для решения задач оптимизации, называется экстремальным. Это название связано с глубокой аналогией между оптимизацией и поиском экстремума некоторой функции. Задача является экстремальной, если цель ее состоит в поиске экстремума некоторой функции. Чтобы установить, какая из двух задач является экстремальной, надо обратиться к их формулировкам и выяснить, где удовлетворяются требования экстремальности.

Цель планирования эксперимента Планирование эксперимента (англ. experimental design techniques) — комплекс мероприятий, направленных на эффективную постановку опытов. Основная цель планирования эксперимента — достижение максимальной точности измерений при минимальном количестве проведенных опытов и сохранении статистической достоверности результатов.

Цель планирования эксперимента Методы планирования эксперимента позволяют минимизировать число необходимых испытаний, установить рациональный порядок и условия проведения исследований в зависимости от их вида и требуемой точности результатов. Если же по каким либо причинам число испытаний уже ограничено, то методы дают оценку точности, с которой в этом случае будут получены результаты. Они базируются на методах теории вероятности и математической статистики.

Этапы планирования эксперимента 1. Установление цели эксперимента (определение характеристик, свойств и т. п. ) и его вида (определительные, контрольные, сравнительные, исследовательские). 2. Уточнение условий проведения эксперимента (имеющееся или доступное оборудование, сроки работ, финансовые ресурсы, численность и кадровый состав работников и т. п. ). Выбор вида испытаний (нормальные, ускоренные, сокращенные в условиях лаборатории, на стенде, полигонные, натурные или эксплуатационные).

Этапы планирования эксперимента 3. Выявление и выбор входных и выходных параметров на основе сбора и анализа предварительной информации. Входные параметры (факторы) могут быть детерминированными, то есть регистрируемыми и управляемыми (зависимыми от наблюдателя), и случайными, то есть регистрируемыми, но неуправляемыми. Наряду с ними на состояние исследуемого объекта могут оказывать влияние нерегистрируемые и неуправляемые параметры, которые вносят систематическую или случайную погрешность в результаты измерений. Это — ошибки измерительного оборудования, изменение свойств исследуемого объекта в период эксперимента, например, из за старения материала или его износа, воздействие персонала и т. д.

Этапы планирования эксперимента 4. Установление потребной точности результатов измерений (выходных параметров), области возможного изменения входных параметров, уточнение видов воздействий. На назначение степени точности влияют условия изготовления и эксплуатации объекта, при создании которого будут использоваться эти экспериментальные данные. Условия изготовления, то есть возможности производства, ограничивают наивысшую реально достижимую точность. Условия эксплуатации, то есть условия обеспечения нормальной работы объекта, определяют минимальные требования к точности.

Этапы планирования эксперимента Точность экспериментальных данных также существенно зависит от объёма (числа) испытаний — чем испытаний больше, тем (при тех же условиях) выше достоверность результатов. Для ряда случаев (при небольшом числе факторов и известном законе их распределения) можно заранее рассчитать минимально необходимое число испытаний, проведение которых позволит получить результаты с требуемой точностью.

Этапы планирования эксперимента 5. Составление плана и проведение эксперимента — количество и порядок испытаний, способ сбора, хранения и документирования данных. Порядок испытаний также важен : в зависимости от выбранной последовательности действий при экспериментальном поиске оптимального соотношения параметров объекта (процесса) может потребоваться больше или меньше опытов. Эти экспериментальные задачи подобны математическим задачам численного поиска оптимальных решений. Наиболее хорошо разработаны методы одномерного поиска (однофакторные однокритериальные задачи), такие как метод Фибоначчи, метод золотого сечения.

Этапы планирования эксперимента 6. Статистическая обработка результатов эксперимента, построение математической модели поведения исследуемых характеристик. Необходимость обработки вызвана тем, что выборочный анализ отдельных данных, вне связи с остальными результатами, или же некорректная их обработка могут не только снизить ценность практических рекомендаций, но и привести к ошибочным выводам. Обработка результатов включает:

Обработка результатов • определение доверительного интервала среднего значения и дисперсии (или среднего квадратичного отклонения) величин выходных параметров (экспериментальных данных) для заданной статистической надежности; • проверка на отсутствие ошибочных значений (выбросов), с целью исключения сомнительных результатов из дальнейшего анализа. Проводится на соответствие одному из специальных критериев, выбор которого зависит от закона распределения случайной величины и вида выброса; • проверка соответствия опытных данных ранее априорно введенному закону распределения. В зависимости от этого подтверждаются выбранный план эксперимента и методы обработки результатов, уточняется выбор математической модели.

Обработка результатов • Построение математической модели выполняется в случаях, когда должны быть получены количественные характеристики взаимосвязанных входных и выходных исследуемых параметров. Это — задачи аппроксимации, то есть выбора математической зависимости, наилучшим образом соответствующей экспериментальным данным. Для этих целей применяют регрессионные модели, которые основаны на разложении искомой функции в ряд с удержанием одного (линейная зависимость, линия регрессии) или нескольких (нелинейные зависимости) членов разложения (ряды Фурье, Тейлора). Одним из методов подбора линии регрессии является широко распространенный метод наименьших квадратов.

Обработка результатов • Для оценки степени взаимосвязанности факторов или выходных параметров проводят корреляционный анализ результатов испытаний. В качестве меры взаимосвязанности используют коэффициент корреляции: для независимых или нелинейно зависимых случайных величин он равен или близок к нулю, а его близость к единице свидетельствует о полной взаимосвязанности величин и наличии между ними линейной зависимости.

Обработка результатов • При обработке или использовании экспериментальных данных, представленных в табличном виде, возникает потребность получения промежуточных значений. Для этого применяют методы линейной и нелинейной (полиноминальной) интерполяции(определение промежуточных значений) и экстраполяции (определение значений, лежащих вне интервала изменения данных).

Анализ результатов 7. Объяснение полученных результатов и формулирование рекомендаций по их использованию, уточнению методики проведения эксперимента. Снижение трудоемкости и сокращение сроков испытаний достигается применением автоматизированных экспериментальных комплексов. Такой комплекс включает испытательные стенды с автоматизированной установкой режимов (позволяет имитировать реальные режимы работы), автоматически обрабатывает результаты, ведет статистический анализ и документирует исследования.

Анализ результатов Планирование эксперимента – это новый подход к исследованию, в котором математическим методам отводится ведущая роль, когда экспериментатор, основываясь на априорных данных, выбирает оптимальную модель, а на апостериорных – ее корректирует.

Предпосылки проведения эксперимента Большинство исследуемых процессов относится к классу сложных систем, характеризуемых значительным числом взаимосвязанных параметров. Задача исследования та ких систем заключается в установлении зависимости между входными параметрами (влияющими факторами) и показате лями качества функционирования систем (выходными показа телями), а также определении уровней (значений) факторов, оптимизирующих выходные показатели.

Предпосылки проведения эксперимента В условиях неполного знания сущности исследуемого процесса задачи идентификации и оптимизации, т. е. отыска ния оптимальных условий протекания процесса или опти мального выбора состава многокомпонентных систем, реша ются с помощью экспериментально статистических методов. В этом случает модель процесса (объекта исследования) удоб но представить в виде кибернетической системы «черного ящика» .
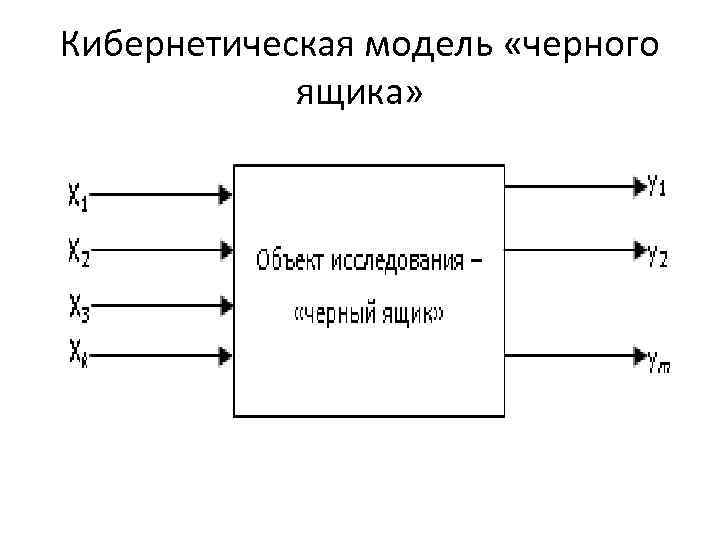
Кибернетическая модель «черного ящика»

Предпосылки проведения эксперимента • Исследование процесса целесообразно осуществлять экс периментально, причем эксперимент должен быть организо ван рациональным образом. • Современное планирование эксперимента отличается от классического подхода тем, что всегда исследуются одновре менно по меньшей мере два фактора. • классические методы не позво ляют определить взаимодействие факторов, оп тимальная бласть процесса при этом о может быть вообще не найдена.

Основные принципы пла нирования эксперимента: а) повторение (дублирование) опытов, позволяющее оце нить ошибку эксперимента и привести к ее уменьшению; б) рандомизация (случайное распределение), позволяю щая получить несмещенные оценки интересующих исследо вателя эффектов путем исключения известных и неизвест ных систе матических ошибок, которые обусловлены факто рами вре мени и пространства, и обеспечить одновременно независи мость результатов эксперимента.

Основные принципы пла нирования эксперимента: Решение задачи начинается с ее формулировки. Исследо ватель олжен иметь четкое, д однозначное представление о цели работы. Желательно, чтобы цель исследования была сформулирована количественно. Целе сообразно, чтобы выходной показатель был однозначным, ха рактеризовался числами, действительно определял оптимум. Лучше, чтобы показатель был только один, имел ясный физический смысл и оценивался с максимальной статистической эффективностью.

Основные принципы пла нирования эксперимента: Не менее сложно выбрать факторы, влияющие на измене ние выходного показателя. Опасно не учесть какой либо сильно влияющий фактор, вся работа окажется бесполезной. Рекомендуется учитывать область, ограничи вающую их возможное варьирование. Каждый фактор может принимать в опыте одно из не скольких значений, называемых уровнями. Каждому фиксиро ванному набору уровней факторов соответствует определен ная точка в многомерном (k мерном, где k — число факторов) факторном пространстве.

Основные этапы пла нирования эксперимента: • На различные наборы уровней факторов система реагирует по разному. Однако существует вполне определенная связь между уровнями факторов и реакцией (откликом) системы. Эта связь характеризуется математическими моделями: Функцию , связывающую параметр оптимизации (вы ход ной показатель ) с факторами , называют функ цией от клика, а геометрический образ, соответствующий функции отклика, — поверхностью отклика
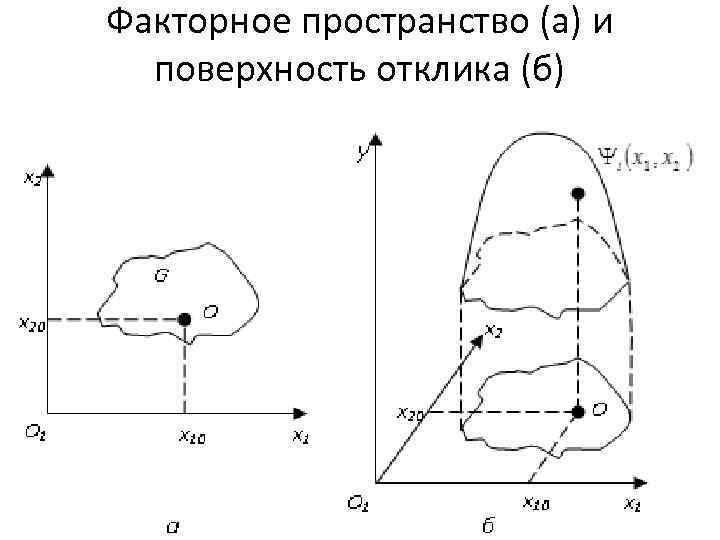
Факторное пространство (а) и поверхность отклика (б)

Основные принципы пла нирования эксперимента:

Основные этапы пла нирования эксперимента: Далее следует от системы координат перейти к новой безразмерной системе координат (т. е. к кодированным значениям факторов). Следующий этап планирования эксперимента — составление линейного плана, реализация опытов которого имеет целью определение линейной математической модели исследуемого процесса. В полном факторном эксперименте (ПФЭ) реализуются все возможные сочетания уровней факторов. Если число уровней каждого фактора равно двум (верхний и нижний), то имеем ПФЭ типа 2 к. Общее число непараллельных опытов такого ПФЭ определяется как n = 2 к.

Основные этапы пла нирования эксперимента: Составляется матрица полного факторного эксперимента типа 2 к , где строки соответствуют различным опытам, а столбцы — значениям факторов в кодированном виде. Часть столбцов матрицы является собственно планом эксперимента, остальные столбцы необходимы для обработки полученных результатов.
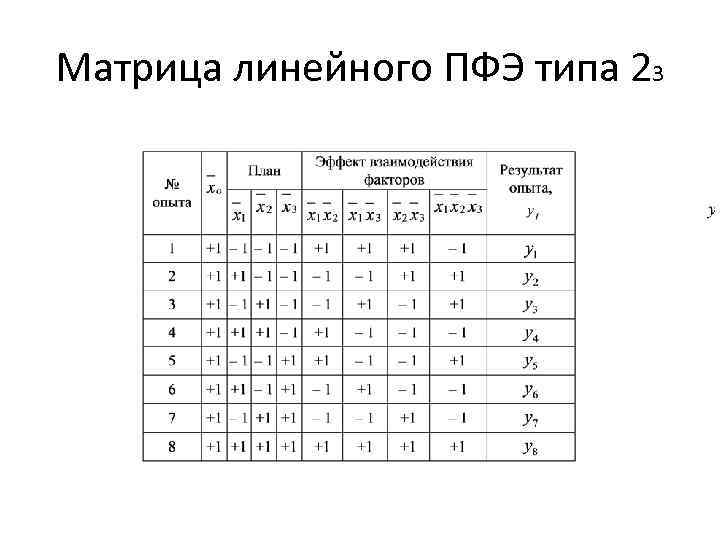
Матрица линейного ПФЭ типа 23

Обработка результатов многофакторного эксперимента Результаты матрицы обрабатываются для определения полиномиального регрес сионного уравнения вида: которое содержит оценку влияния на выходной показатель факторов, их парных и тройных взаимодействий.

Обработка результатов многофакторного эксперимента Численное значение коэффициентов регрессии определяется в соответствии с методами матричной алгебры: где В — матрица столбец коэффициентов регрессии; Хт — транспонированная матрица планирования эксперимента; Y — матрица столбец результатов эксперимента.

Обработка результатов многофакторного эксперимента Для матрицы 23 получаем:

Обработка и анализ Далее осуществляются статистические проверки: на значимость коэффициентов регрессии, на достоверность математической модели, на нормальность распределения результатов опытов и др. После этого осуществляют переход от кодированных переменных к натуральным в уравнении (5. 5) по формуле (5. 4). по найденной регрессионной модели целесообразно построить графические зависимости типа:
Планир_эксперим.pptx