ПЛАНИМЕТРИЯ Планиметрия от лат planum плоскость

ПЛАНИМЕТРИЯ

Планиметрия (от лат. planum — «плоскость» , др. -греч. μετρεω — «измеряю» ) — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости.

• Первое систематическое изложение планиметрии впервые было дано Евклидом в его труде «Начала» .

ИЗУЧАЕМЫЕ ПЛАНИМЕТРИЕЙ • Точка • Прямая • Параллелограмм (ч астные случаи: • квадрат, прямоуголь ник, ромб) • Трапеция • Окружность • Треугольник • Многоугольник

ТОЧКА Точкой называют абстрактный объект в пространстве, не имеющий ни объёма, ни площади, ни длины, ни какихлибо других измеримых характеристик. Таким образом, точкой называют нульмерный объект. Евклид определил точку как «объект, не имеющий частей» . В выбранной системе координат, любую точку двумерного евклидова пространства можно

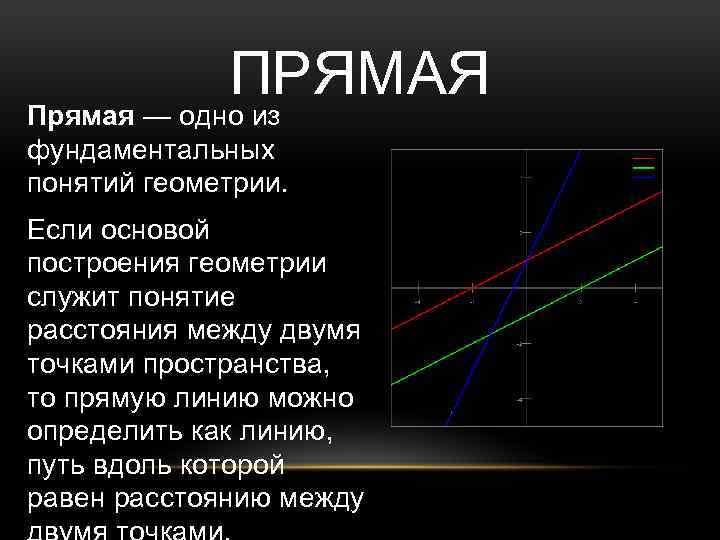ПРЯМАЯ Прямая — одно из фундаментальных понятий геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между

•

СВОЙСТВА ПРЯМОЙ В ЕВКЛИДОВОЙ ГЕОМЕТРИИ • Через любую точку можно провести бесконечно много прямых. • Через любые две несовпадающие точки можно провести единственную прямую. • Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными. • В декартовой системе координат прямая линия задается на плоскости уравнением

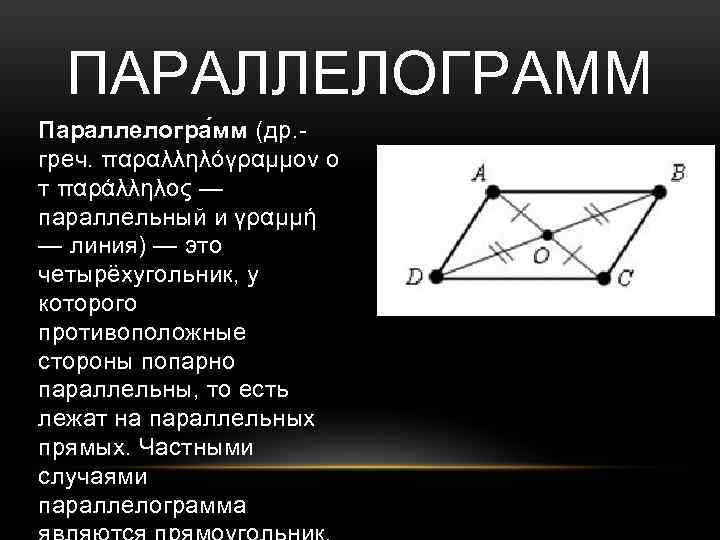ПАРАЛЛЕЛОГРАММ Параллелогра мм (др. греч. παραλληλόγραμμον о т παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма

СВОЙСТВА ПАРАЛЛЕЛОГРАММА •

ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА •

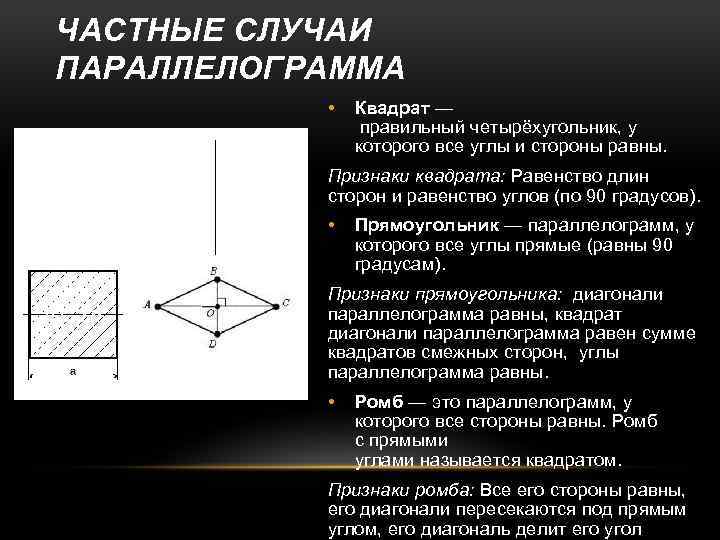ЧАСТНЫЕ СЛУЧАИ ПАРАЛЛЕЛОГРАММА • Квадрат — правильный четырёхугольник, у которого все углы и стороны равны. Признаки квадрата: Равенство длин сторон и равенство углов (по 90 градусов). • Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Признаки прямоугольника: диагонали параллелограмма равны, квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, углы параллелограмма равны. • Ромб — это параллелограмм, у которого все стороны равны. Ромб с прямыми углами называется квадратом. Признаки ромба: Все его стороны равны, его диагонали пересекаются под прямым углом, его диагональ делит его угол

ТРАПЕЦИЯ Трапеция (от др. греч. τραπέζιον — «столик» ; τράπεζα — «стол, еда» ) — четырёхугольник, у которого только пара сторон параллельна. Две параллельные стороны называются основаниями трапеции, а две другие — это боковые стороны. Виды трапеций • Трапеция, у которой боковые стороны равны, называется равнобокой, равнобочной или равнобедр енной. • Трапеция, имеющая прямые углы при

ОБЩИЕ СВОЙСТВА ТРАПЕЦИИ •

ОКРУЖНОСТЬ •

СВЯЗАННЫЕ С ОКРУЖНОСТЬЮ ОПРЕДЕЛЕНИЯ • Радиус — не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек. • Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром. • Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии. • Любые две не совпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром. • Угол, образуемый дугой окружности, равной по длине радиусу, принимается за 1 радиан. • Длина единичной полуокружности обозначается через π.

• Геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое, называется кругом. • Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. • Прямая, проходящая через две различных точки окружности, называется секущей. • Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается. • Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается. • Две окружности, имеющие общий центр, называются концентрическими. • Две окружности, пересекающиеся под прямым углом, называются ортогональными

ТРЕУГОЛЬНИКИ Треугольник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треуголь ника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Если три точки лежат на одной прямой, то «треугольник» с вершинами в трёх данных точках называется вырожденным. Все

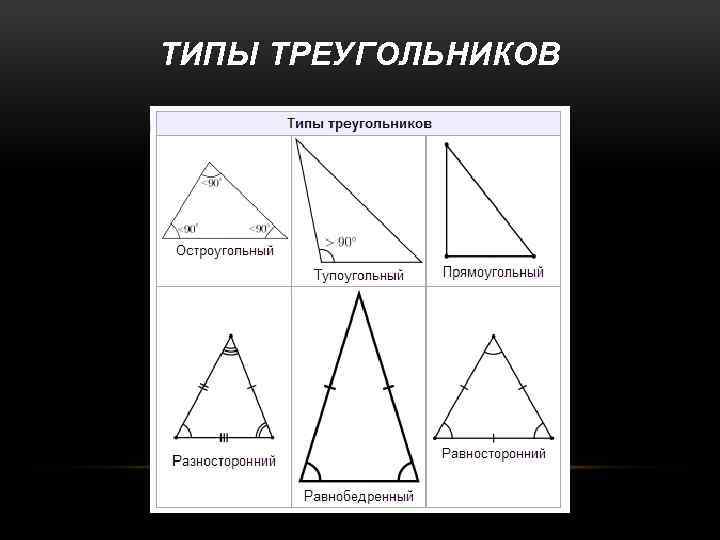ТИПЫ ТРЕУГОЛЬНИКОВ

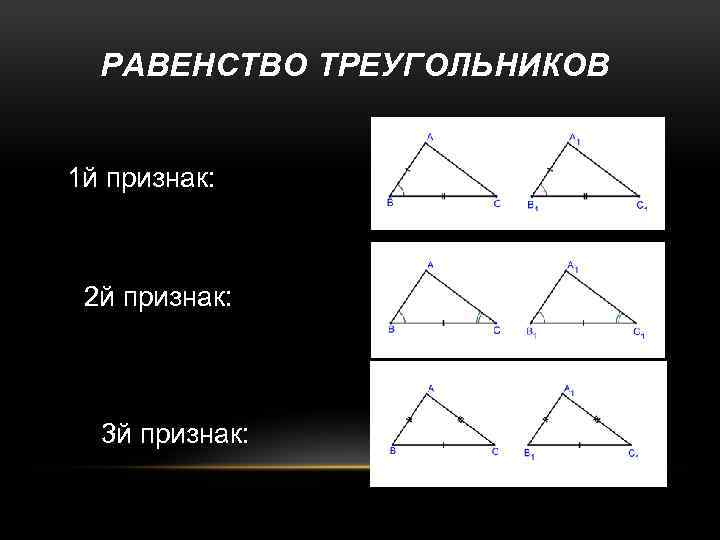РАВЕНСТВО ТРЕУГОЛЬНИКОВ 1 й признак: 2 й признак: 3 й признак:

МНОГОУГОЛЬНИК Многоугольник — это геометрическая фигура, обычно определяется как замкнутая ломаная. Существуют три различных варианта определения многоугольника: • Плоская замкнутая ломаная — самый общий случай; • Плоская замкнутая ломаная без самопересечений — простой многоугольник; • Часть плоскости, ограниченная замкнутой ломаной без

СВОЙСТВА И СВЯЗАННЫЕ ОПРЕДЕЛЕНИЯ Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями. Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый. Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом, он может принимать значения от -180° до 180°. Свойства: 1. Сумма внутренних углов плоского выпуклого n-угольника равна 180°(n-2).

ВИДЫ МНОГОУГОЛЬНИКОВ • Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д. Многоугольник с n вершинами называется n-угольником. • Плоским многоугольником называется фигура, которая состоит из многоугольника и ограниченной им конечной части площади. • Многоугольник называют выпуклым, если выполнено одно из следующих (эквивалентных) условий: ü Он лежит по одну сторону от любой прямой, соединяющей его соседние вершины. (то есть продолжения сторон многоугольника не пересекают других его сторон); ü Он является пересечением (то есть общей частью) нескольких полуплоскостей; ü Каждая диагональ лежит внутри многоугольника; ü Любой отрезок с концами в точках, принадлежащих многоугольнику, целиком ему принадлежит. • Если некоторые внутренние углы равны 180°, а остальные меньше, то многоугольник называется слабовыпуклым. Выпуклый многоугольник называется правильным, если у него равны все стороны и все углы, например равносторонний треугольник , квадрат и правильный пятиугольник. • Не выпуклый многоугольник у которого равны все стороны и все углы, а вершины совпадают с вершинами некоторого правильного многоугольника называется правильным звёздчатым многоугольником. Такой многоугольник имеет самопересечения, например, пентаграмма и гексаграмма. • Выпуклый многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.

ПРЕЗЕНТАЦИЮ ВЫПОЛНИЛА студентка группы 09 фв 1 Журавлёва Анастасия Спасибо за