Планетарные передачи Студент группы КТО-33 Д Васьков В

Планетарные передачи Студент группы КТО-33 Д Васьков В. Л. Преподаватель Сажина И. В.

I)Назначение и область применения планетарных передач Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями. Планетарную передачу применяют как: qредуктор с постоянным передаточным числом; q коробку скоростей, передаточное число в которой изменяется путём поочерёдного торможения различных звеньев (водила или одного из колёс); qдифференциальный механизм.

Их успешно применяют в транспортном машиностроении, станкостроении, приборостроении и т. д. Имеется большое количество различных типов планетарных передач, но одноступенчатая планетарная передача получила самое широкое распространение , т. к. с успехом применяется как для больших, так и малых мощностей в силовых и кинематических приводах, т. е. не имеет ограничений по применению. КПД передачи η=0, 96… 0, 98. В передачах применяют не только цилиндрические, но и конические колёса. Зубья могут быть прямые и косые. Обычно число сателлитов С = 3… 6, но встречаются передачи с С > 6. Наибольшее распространение получили прямозубые передачи с числом сателлитов С = 3.

II)Устройство Планетарная передача состоит из: qнеподвижного центрального колеса(1) с наружными зубьями; qсателлитов (2); qбольшого центрального колеса (эпицикла, короны)(3) с внутренними зубьями и водила (Н), на котором укреплены оси сателлитов.

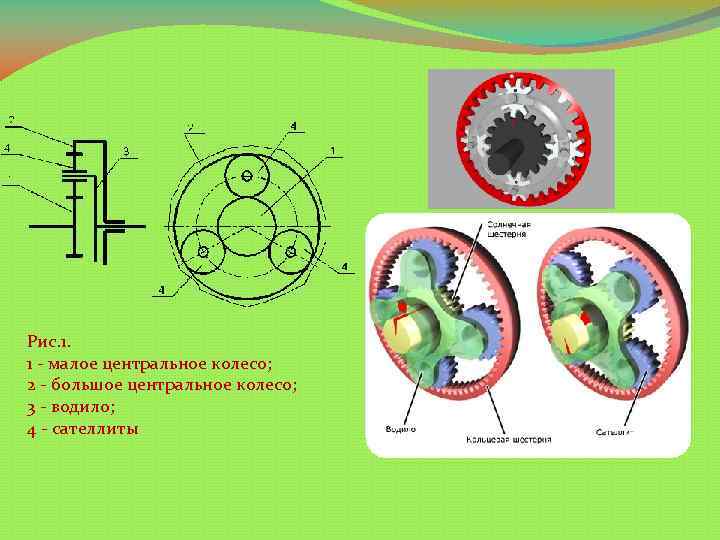Рис. 1. 1 - малое центральное колесо; 2 - большое центральное колесо; 3 - водило; 4 - сателлиты

Основным параметром, определяющим свойства планетарного механизма (ряда), является внутреннее передаточное отношение. В общем случае любой планетарный ряд характеризуется шестью внутренними передаточными отношениями. Однако, на практике обычно используется только одно, определяемое как отношение частоты вращения малого центрального к частоте вращения большого центрального колеса при остановленном водиле: где 1 - индекс малого центрального колеса; 2 - индекс большого центрального колеса; 3 - индекс водила. В зависимости от того, как вращаются центральные колеса при остановленном водиле, внутреннее передаточное отношение планетарного ряда может быть либо положительным, либо отрицательным. Если они вращаются в одном и том же направлении, то внутреннее передаточное отношение положительное, в противном случае оно отрицательное. Так для простого планетарного ряда, представленного на рис. 1, центральные колеса при остановке водила будут вращаться в различных направлениях, и, следовательно, внутреннее передаточное отношение этого ряда -

• Уравнение, связывающее угловые скорости (ω) трех основных звеньев любого планетарного ряда (не зависимо от схемы построения) выглядит следующим образом: Где 1 - индекс малого центрального колеса; 2 - индекс большого центрального колеса; 3 - индекс водила. • Величина внутреннего передаточного отношения планетарного ряда i 12 Где z 1 - число зубьев малого центрального колеса; z 2 - число зубьев большого центрального колеса. • Для планетарных рядов с двухвенцовыми сателлитами эта величина может быть определена следующим образом: Где zст1 - число зубьев сателлита, сцепленного с малым центральным колесом; zст2 - число зубьев сателлита, сцепленного с большим центральным

III)Принцип работы планетарной передачи Сателлиты обкатываются по центральным колесам и вращаются вокруг своих осей, то есть совершают движение, подобное движению планет. Водило вместе с сателлитами вращается вокруг центральной оси. При неподвижном центральном колесе 3 движение может передаваться от центрального колеса 1 к водилу Н или от водила к колесу 1. В случае неподвижного водила движение может передаваться от колеса 1 к колесу 3 или от колеса 3 к колесу 1. Планетарную передачу, в которой одно из центральных колёс неподвижно, называют простейшей. В отличие от простейшей планетарную передачу, в которой все зубчатые колёса и водило подвижны (свободны), называют дифференциальной. В дифференциальной передаче одно движение можно раскладывать на два или два движения сложить в одно. Например, движение колеса 3 можно передавать одновременно колесу 1 и водилу Н или от колес 1 и 3 водилу Н.

IV)Плюсы и минусы планетарных передач Плюсы 1) Большое передаточное число в одной ступени; 2) Малые габариты и масса. Это объясняется следующим: мощность передается по нескольким потокам, число которых равно числу сателлитов; 3) Повышенная нагрузочная способность, так как широко применяются зубчатые колёса с внутренним зацеплением (большой радиус кривизны); 4) Малая нагрузка на опоры, так как сателлиты расположены симметрично, и поэтому силы в передаче взаимно уравновешивают друга; 5) Планетарные передачи работают с меньшим шумом, что связанно с повышенной плавностью внутреннего зацепления и меньшими размерами колёс. Минусы 1) Повышенные требования к точности изготовления и монтажа; 2) Резкое снижение КПД передачи с увеличением передаточного числа (увеличение количества трущихся поверхностей).

V)Классификация планетарных передач В зависимости от знака внутреннего передаточного отношения планетарные передачи делят на: 1)) Планетарные ряды с положительным внутренним передаточным отнош 1 - малое центральное колесо; 2 - большое центральное колесо; 3 - водило; 4 - одновенцовые сателлиты; Рис. 1 5 - двухвенцовые сателлиты. Планетарные ряды, изображенные на рисунках (1 а) и (1 в) построены с использованием двухвенцовых сателлитов.

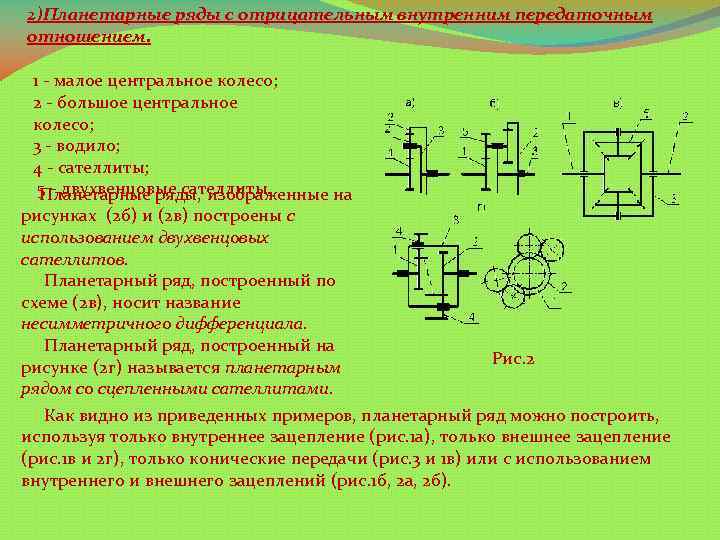2)Планетарные ряды с отрицательным внутренним передаточным отношением. 1 - малое центральное колесо; 2 - большое центральное колесо; 3 - водило; 4 - сателлиты; 5 - двухвенцовые сателлиты. Планетарные ряды, изображенные на рисунках (2 б) и (2 в) построены с использованием двухвенцовых сателлитов. Планетарный ряд, построенный по схеме (2 в), носит название несимметричного дифференциала. Планетарный ряд, построенный на Рис. 2 рисунке (2 г) называется планетарным рядом со сцепленными сателлитами. Как видно из приведенных примеров, планетарный ряд можно построить, используя только внутреннее зацепление (рис. 1 а), только внешнее зацепление (рис. 1 в и 2 г), только конические передачи (рис. 3 и 1 в) или с использованием внутреннего и внешнего зацеплений (рис. 1 б, 2 а, 2 б).

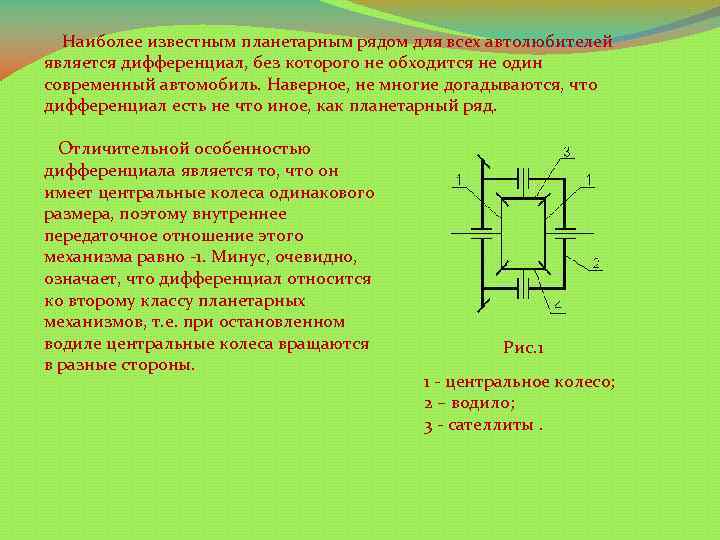Наиболее известным планетарным рядом для всех автолюбителей является дифференциал, без которого не обходится не один современный автомобиль. Наверное, не многие догадываются, что дифференциал есть не что иное, как планетарный ряд. Отличительной особенностью дифференциала является то, что он имеет центральные колеса одинакового размера, поэтому внутреннее передаточное отношение этого механизма равно -1. Минус, очевидно, означает, что дифференциал относится ко второму классу планетарных механизмов, т. е. при остановленном водиле центральные колеса вращаются в разные стороны. Рис. 1 1 - центральное колесо; 2 – водило; 3 - сателлиты.

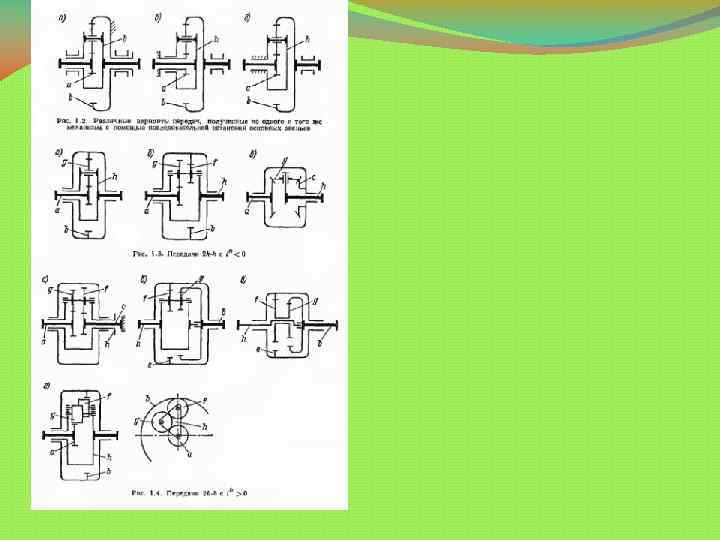
VI)Свойства 1. Свойство блокировки планетарного ряда. Нетрудно показать, что если угловые скорости двух звеньев планетарного ряда равны, то и угловая скорость третьего звена будет равна угловой скорости этих двух звеньев. Пусть, например, ω1= ω 3, тогда: или т. е. угловые скорости всех звеньев в этом случае равны, и планетарный ряд будет вращаться как одно целое тело. Аналогичный результат можно получить и в двух других случаях, когда ω 1= ω 2 и ω 2= ω3. Отсюда вытекает известное свойство блокировки планетарного ряда: если установить блокировочную муфту между любыми двумя звеньями планетарного ряда (рис. 1), то при ее Рис. 1 включении планетарный ряд будет заблокирован, и его передаточное 1 - малое центральное колесо; отношение будет равно 1. 2 - большое центральное колесо; 3 - водило; 4 - блокировочная муфта

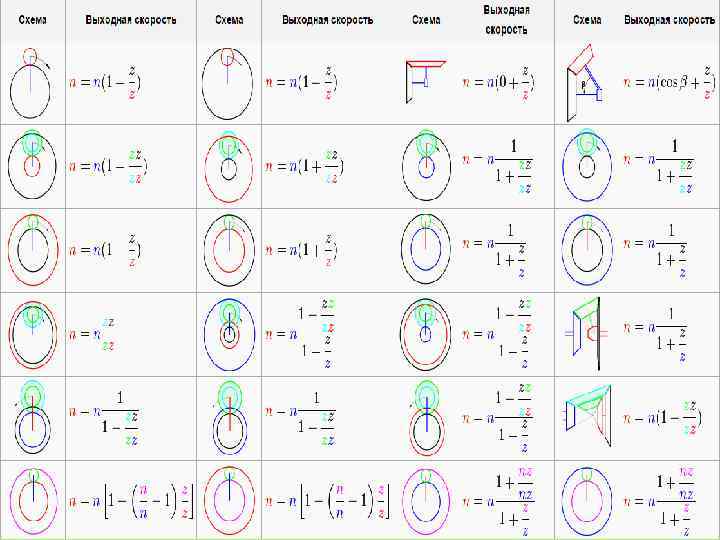
2. Свойство работать в редукторном режиме. Рассмотрим это свойство на примере планетарного ряда второго класса, т. е. с отрицательным внутренним передаточным отношением (i 12<0). Здесь возможны два варианта. Первый. Пусть большое центральное колесо будет остановлено (ω 2=0), водило назначим ведомым звеном планетарного ряда, а малое центральное колесо - ведущим звеном (рис. 2 а). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью: т. е. получаем редуктор, передаточное отношение которого на единицу больше внутреннего передаточного отношения самого планетарного ряда. Рис. 2 Варианты работы планетарного ряда в режиме редуктора.

Второй. Пусть большое центральное колесо будет ведущим звеном планетарного ряда, водило - ведомым звеном, а малое центральное колесо - остановлено, (ω=0) (рис. 2 б). Тогда после небольшого преобразования (1) получим: Рис. 2 Варианты работы планетарного ряда в режиме редуктора. т. е. получаем редуктор, передаточное отношение которого близко к единице.

3. Свойство работать в режиме повышающей передачи. Опять-таки, рассмотрим это свойство на примере планетарного ряда второго класса, т. е. с отрицательным внутренним передаточным отношением (i 12<0). Здесь также возможны два варианта. Первый. Пусть большое центральное колесо будет остановлено (ω2=0), водило - ведущим звеном планетарного ряда, а малое центральное колесо - ведомым звеном (рис. 3 а). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью: Рис. 3 Варианты работы планетарного ряда в режиме повышающей передачи.

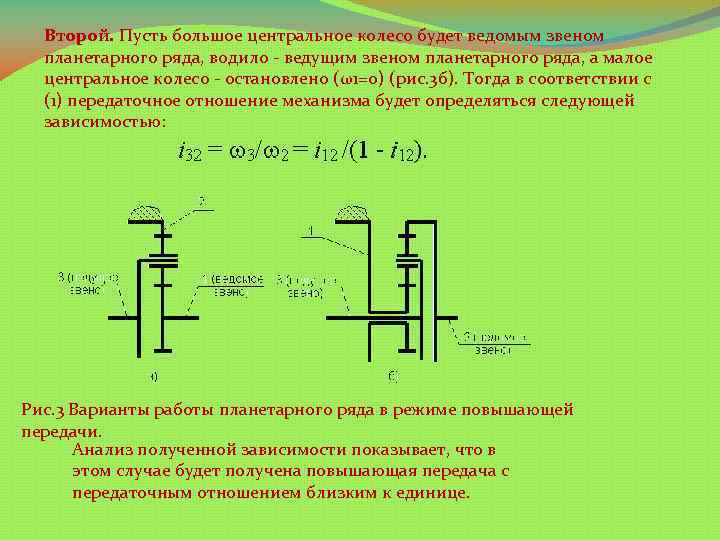Второй. Пусть большое центральное колесо будет ведомым звеном планетарного ряда, водило - ведущим звеном планетарного ряда, а малое центральное колесо - остановлено (ω1=0) (рис. 3 б). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью: Рис. 3 Варианты работы планетарного ряда в режиме повышающей передачи. Анализ полученной зависимости показывает, что в этом случае будет получена повышающая передача с передаточным отношением близким к единице.

4. Свойство реверсивности. Использование этого свойства позволяет организовать передачу заднего хода. Так же, как и в трех предыдущих случаях исследуем возможности реверсивного свойства на примере планетарного ряда второго класса. Здесь возможны, опять-таки два варианта. Первый. Пусть большое центральное колесо будет ведомым звеном планетарного ряда, водило - остановлено (ω3=0), а малое центральное колесо - ведущим звеном (рис. 4 а). Тогда в соответствии с (1) передаточное отношение механизма будет равно внутреннему передаточному отношению планетарного ряда: Поскольку для планетарных механизмов второго класса внутреннее передаточное отношение отрицательное, то получаем редуктор с отрицательным передаточным отношением Рис. 4 Варианты работы планетарного ряда в режиме передачи заднего хода.

Второй. Пусть большое центральное колесо будет ведущим звеном планетарного ряда, водило - остановлено (ω3=0), а малое центральное колесо - ведомым звеном (рис. 4 а). Тогда: Т. е. получаем мультипликатор с отрицательным передаточным отношением (поскольку i 12<0). Рис. 4 Варианты работы планетарного ряда в режиме передачи заднего хода.

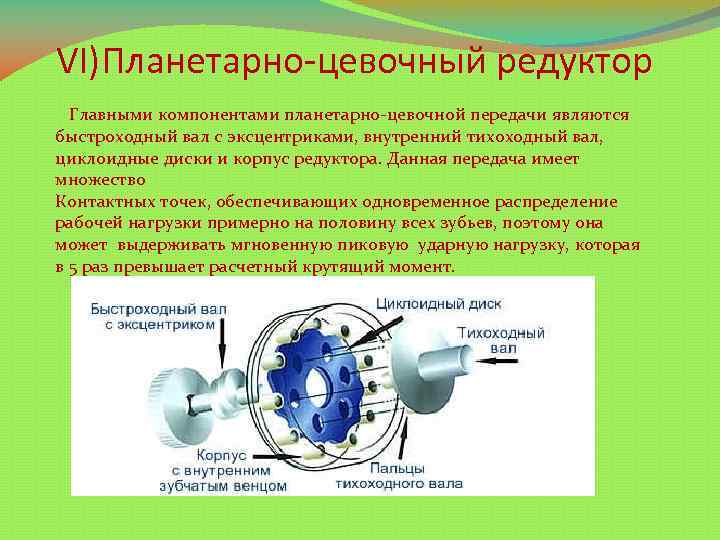VI)Планетарно-цевочный редуктор Главными компонентами планетарно-цевочной передачи являются быстроходный вал с эксцентриками, внутренний тихоходный вал, циклоидные диски и корпус редуктора. Данная передача имеет множество Контактных точек, обеспечивающих одновременное распределение рабочей нагрузки примерно на половину всех зубьев, поэтому она может выдерживать мгновенную пиковую ударную нагрузку, которая в 5 раз превышает расчетный крутящий момент.

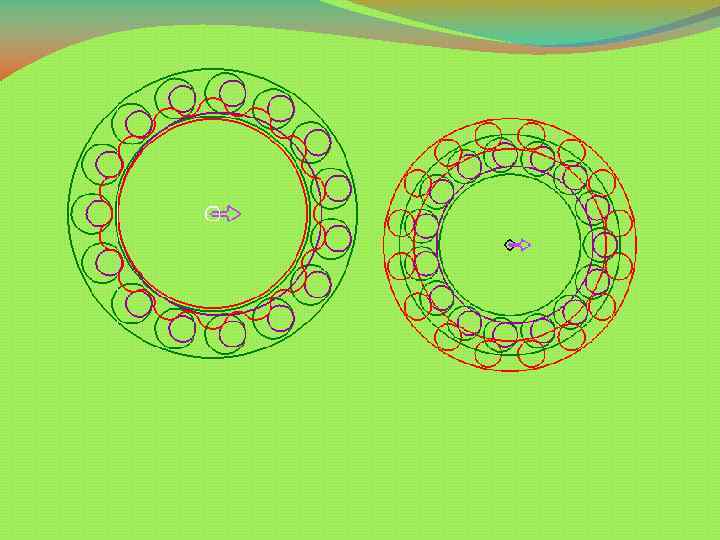
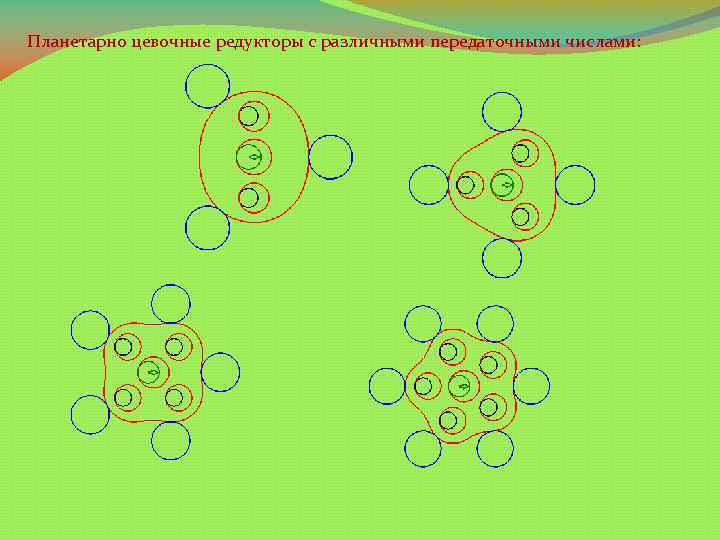Планетарно цевочные редукторы с различными передаточными числами:

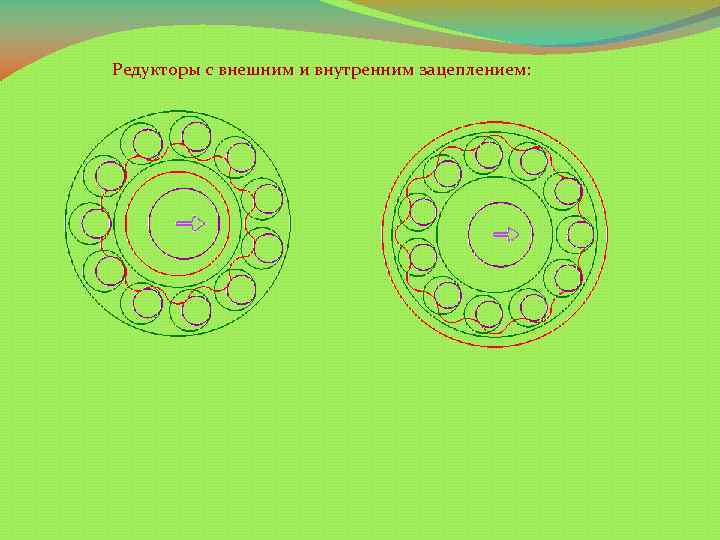Редукторы с внешним и внутренним зацеплением:

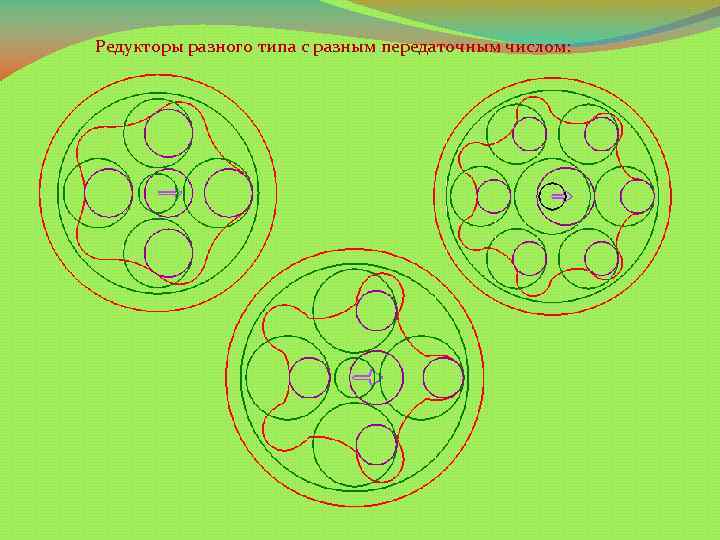Редукторы разного типа с разным передаточным числом:

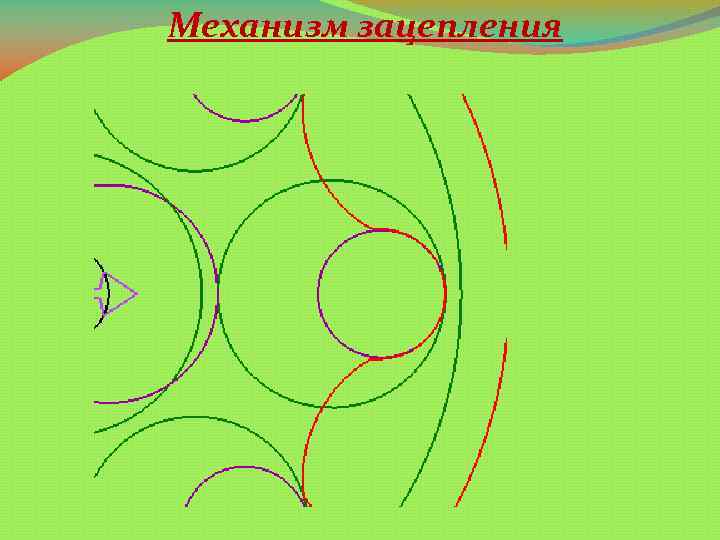Механизм зацепления

Спасибо за внимание