МС2011 тема 2 с практикой NEW.ppt
- Количество слайдов: 76


ПЛАН ТЕМЫ l l l 2 Общие сведения о выборочном методе Понятие об оценке параметров. Виды оценок Точечные оценки параметров распределения Законы распределения выборочных характеристик, используемые при интервальной оценке параметров Интервальные оценки параметров распределения Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011

Общие сведения о выборочном методе l Виды наблюдений: § сплошное § выборочное Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 3
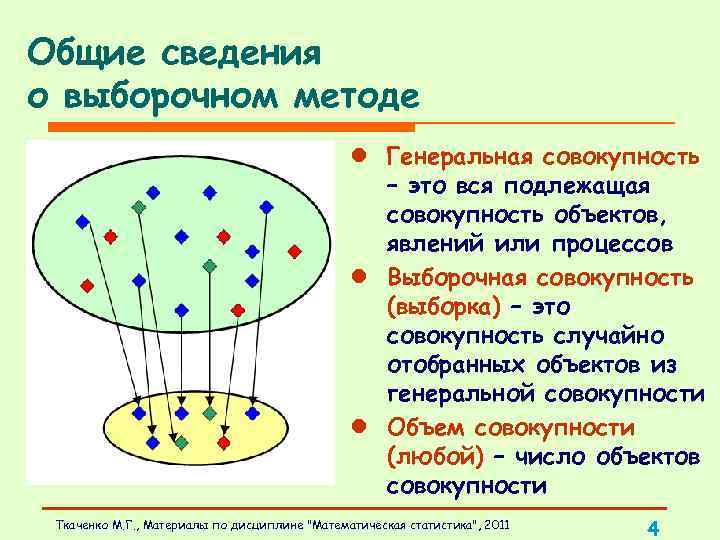
Общие сведения о выборочном методе l Генеральная совокупность – это вся подлежащая совокупность объектов, явлений или процессов l Выборочная совокупность (выборка) – это совокупность случайно отобранных объектов из генеральной совокупности l Объем совокупности (любой) – число объектов совокупности Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 4

Общие сведения о выборочном методе l Преимущества выборочного метода: § Позволяет экономить затраты ресурсов § Является единственно возможным в некоторых случаях: o в случае бесконечной генеральной совокупности o в случае, когда исследование связано с уничтожением наблюдаемых объектов § При тех же затратах ресурсов дает возможность проведения углубленного исследования § Позволяет снизить ошибки регистрации Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 5

Общие сведения о выборочном методе l Основной недостаток – ошибки репрезентативности (представительства). l Репрезентативная выборка – это выборка, достаточно хорошо воспроизводящая генеральную совокупность. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 6
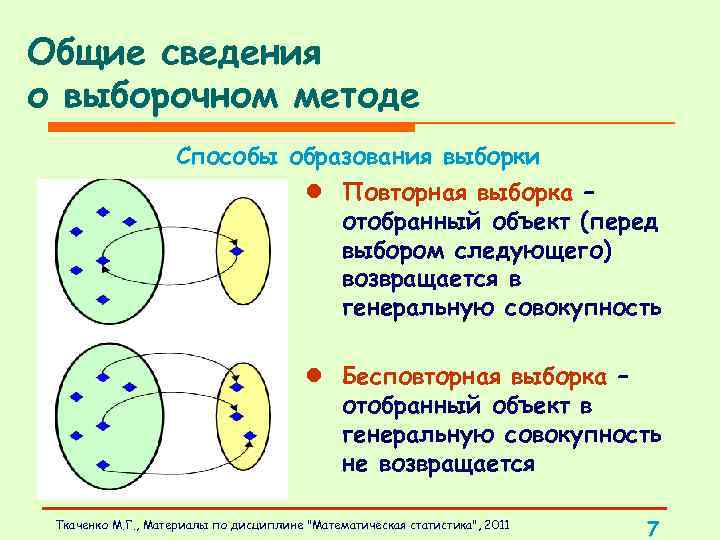
Общие сведения о выборочном методе Способы образования выборки l Повторная выборка – отобранный объект (перед выбором следующего) возвращается в генеральную совокупность l Бесповторная выборка – отобранный объект в генеральную совокупность не возвращается Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 7

Общие сведения о выборочном методе l Виды выборок: § Собственно-случайная выборка § Механическая выборка § Типическая (стратифицированная) выборка § Серийная (гнездовая) выборка Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 8

Общие сведения о выборочном методе l Важнейшая задача выборочного метода – по некоторой части генеральной совокупности (по выборке) оценить параметры генеральной совокупности, вынести суждение о ее свойствах в целом. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 9

Общие сведения о выборочном методе О Б О З Н А Ч Е Н И Я Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 10

Понятие об оценке параметров. Виды оценок Пусть – случайная величина, подчиненная закону распределения , – параметр распределения, числовое значение которого неизвестно. Оценка (или статистика) – всякая однозначно определенная функция результатов наблюдений, с помощью которой судят о значении параметра. Основная задача теории оценивания: Выбор оценки, позволяющей получить хорошее приближение оцениваемого параметра Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 11

Понятие об оценке параметров. Виды оценок параметров распределения: l Точечная оценка § оценка, определяемая одним числом l Интервальная оценка – § оценка, определяемая двумя числами – концами интервала Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 12

Точечные оценки параметров распределения l Основные свойства точечных оценок l Методы получения точечных оценок l Оценки параметров генеральной совокупности по собственно-случайной выборке Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 13

Точечные оценки параметров распределения l Основные свойства точечных оценок § несмещенность § состоятельность § эффективность Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 14

Точечные оценки параметров распределения Несмещенной называется статистическая оценка , если ее математическое ожидание равно оцениваемому параметру при любом объеме выборки: . Смещенной называется статистическая оценка, если математическое ожидание ее не равно оцениваемому параметру. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 15

Точечные оценки параметров распределения Эффективной называется статистическая оценка, если она при заданном объеме выборки имеет наименьшую возможную дисперсию. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 16

Точечные оценки параметров распределения Состоятельной называется статистическая оценка, которая при стремится по вероятности к оцениваемому параметру. Если оценка несмещенная, то она будет состоятельной, если при ее дисперсия стремится к 0. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 17

Точечные оценки параметров распределения l Методы получения точечных оценок: § метод моментов, § метод максимального правдоподобия, § метод наименьших квадратов. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 18

Точечные оценки параметров распределения Метод моментов для получения точечных оценок параметров (предложен К. Пирсоном) основан на том, что начальные или центральные (или те и другие) эмпирические моменты приравниваются соответствующим теоретическим моментам того же порядка. В качестве оценки неизвестного параметра принимается такое значение , которое является решением уравнения или системы уравнений. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 19

Точечные оценки параметров распределения Оценки метода моментов состоятельны, но имеют эффективность много меньше 1. Метод моментов часто используется на практике, так как приводит к сравнительно простым вычислениям Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 20

Точечные оценки параметров распределения Метод максимального правдоподобия для получения точечных оценок параметров (предложен Р. Фишером) основан на том, что в качестве оценки неизвестного параметра принимается такое значение , которое максимизирует функцию правдоподобия. Функция правдоподобия выражает вероятность совместного появления результатов выборки , и т. д. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 21

Точечные оценки параметров распределения Оценки параметров по методу максимального правдоподобия являются состоятельными, асимптотически несмещенными, асимптотически эффективными и имеют нормальное распределение. Основные недостатки метода максимального правдоподобия – § трудность вычисления оценок, связанных с решением уравнений правдоподобия, чаще всего нелинейных. § необходимо точное знание типа анализируемого закона распределения, что во многих случаях практически нереально Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 22

Точечные оценки параметров распределения Метод наименьших квадратов для получения точечных оценок параметров (предложен Лежандром, Р. Адрейном, Гауссом) основан на том, что оценка определяется из условия минимизации суммы квадратов отклонений выборочных данных от определяемой оценки. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 23

Точечные оценки параметров распределения Метод наименьших квадратов § не требует знания закона распределения выборочных данных § достаточно хорошо разработан в плане вычислительной реализации § используется в задачах корреляционного и регрессионного анализа Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 24

Точечные оценки параметров распределения l Оценки параметров генеральной совокупности по собственно-случайной выборке (повторной и бесповторной) § Оценка генеральной доли § Оценка генеральной средней § Оценка генеральной дисперсии Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 25

Точечные оценки параметров распределения Оценка генеральной доли Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 26

Точечные оценки параметров распределения Оценка генеральной средней Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 27

Точечные оценки параметров распределения Оценка генеральной дисперсии Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 28

ПРАКТИКУМ Базовый пример 3: По данным базовых примеров 1 и 2 вычислить несмещенную оценку для генеральной дисперсии и генерального среднего квадратического отклонения. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 29

ПРАКТИКУМ Решение БП 3: Формула для нахождения несмещенной оценки для генеральной дисперсии имеет вид Для нахождения подставим в первую часть формулы найденное ранее значение : • по данным базового примера 1: • по данным базового примера 2: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 30

ПРАКТИКУМ Решение БП 3 (продолжение): Несмещенную оценку для генерального среднего квадратического отклонения вычислим по формуле: • по данным базового примера 1: • по данным базового примера 2: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 31

Законы распределения выборочных характеристик, используемые при интервальной оценке параметров l Распределение Стьюдента (t-распределение) l Распределение Пирсона – ( «хи-квадрат» ) Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 32

Законы распределения выборочных характеристик, используемые при интервальной оценке параметров Пусть имеется несколько нормированных нормально распределенных случайных величин: , , …, ( , ). Тогда сумма их квадратов является случайной величиной, распределенной по так называемому закону ( «хи-квадрат» ) с степенями свободы. Если же слагаемые связаны каким-либо соотношением (например, ), то число степеней свободы. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 33

Законы распределения выборочных характеристик, используемые при интервальной оценке параметров Пусть имеются две независимые случайные величины: – распределенная по нормальному закону и нормированная (то есть , ), - распределенная по закону ( «хи-квадрат» ) с степенями свободы. Тогда величина имеет – распределение или распределение Стьюдента с степенями свободы. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 34

Законы распределения выборочных характеристик, используемые при интервальной оценке параметров С возрастанием числа степеней свободы t -распределение (распределение Стьюдента) быстро приближается к нормальному. С увеличением числа степеней свободы распределение «хи-квадрат» постепенно приближается к нормальному. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 35

Интервальные оценки параметров распределения l l l Понятие интервального оценивания Интервальная оценка для математического ожидания (генеральной средней) при известном среднем квадратическом отклонении (дисперсии) генеральной совокупности Интервальная оценка для математического ожидания (генеральной средней) при неизвестном среднем квадратическом отклонении (дисперсии) генеральной совокупности Интервальная оценка для генерального среднего квадратического отклонения Интервальная оценка для генеральной доли Вычисление объема выборки Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 36

Интервальные оценки параметров распределения Пусть для оценки некоторого параметра справедливо неравенство , Точностью оценки (предельной ошибкой выборки) называется наибольшее отклонение оценки от оцениваемого параметра. Надежностью (доверительной вероятностью, уровнем доверия) оценки параметра называется вероятность того, что выполняется неравенство : . Доверительным называется интервал, который накрывает неизвестный параметр с заданной надежностью. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 37

Интервальные оценки параметров распределения l Интервальная оценка для математического ожидания (генеральной средней) нормального распределения при известном среднем квадратическом отклонении (дисперсии) генеральной совокупности Доверительный интервал: или , где Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 38

Интервальные оценки параметров распределения Порядок построения доверительного интервала для математического ожидания (генеральной средней) при известном среднем квадратическом отклонении (дисперсии) Из условия задачи 1. определить объем выборки для вычисления средней выборочной. 2. определить или вычислить по формуле среднюю выборочную 3. определить генеральное среднее квадратическое отклонение или вычислить его по генеральной дисперсии: 4. по доверительной вероятности (надежности) или уровню значимости определить значение функции (интеграла вероятностей) Лапласа l по найденному в п. 4 значению функции по таблице значений функции Лапласа в ПРИЛОЖЕНИИ 2 на стр. 462463 найти аргумент функции l вычислить точность оценки по выборочным данным и записать доверительный интервал для математического ожидания (генеральной средней) в виде или Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 39

ПРАКТИКУМ Базовый пример 4: По значению функции в ПРИЛОЖЕНИИ 2 на стр. 462 -463 определить аргумент : а) б) в) Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 40
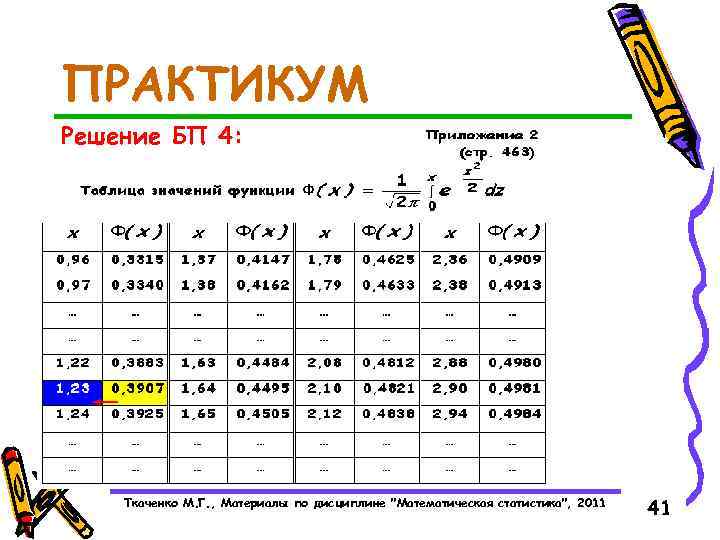
ПРАКТИКУМ Решение БП 4: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 41

ПРАКТИКУМ Решение БП 4 (продолжение): Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 42

ПРАКТИКУМ Базовый пример 5: По результатам 10 наблюдений установлено, что средний темп роста акций предприятий отрасли равен 104, 4%. В предположении, что ошибки наблюдений распределены по нормальному закону со средним квадратическим отклонением 1%, определить с надежностью 0, 95 интервальную оценку для генеральной средней. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 43

ПРАКТИКУМ Решение БП 5: 1. 2. объем выборки средняя выборочная 3. генеральное среднее квадратическое отклонение 4. доверительная вероятность (надежность) определяем значение функции (интеграла вероятностей) Лапласа , Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 44

ПРАКТИКУМ Решение БП 5(продолжение): • • по значению функции в ПРИЛОЖЕНИИ 2 на стр. 462 -463 определяем аргумент вычисляем точность оценки по выборочным данным • доверительный интервал для генеральной средней или • Окончательно получаем доверительный интервал: или Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 45

Интервальные оценки параметров распределения l Интервальная оценка для математического ожидания (генеральной средней) нормального распределения при неизвестном среднем квадратическом отклонении (дисперсии) генеральной совокупности Доверительный интервал: , где или Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 46

Интервальные оценки параметров распределения Из 1. 2. 3. 4. l l Порядок построения доверительного интервала для математического ожидания (генеральной средней) при неизвестном среднем квадратическом отклонении (дисперсии) условия задачи определить объем выборки для вычисления средней выборочной определить или вычислить по формуле среднюю выборочную определить или вычислить по формуле «исправленное» среднее квадратическое отклонение определить надежность (доверительную вероятность) или вычислить ее по уровню значимости по значениям и найти , пользуясь таблицей значений в ПРИЛОЖЕНИИ 3 на стр. 464 вычислить по выборочным данным точность оценки и записать доверительный интервал для математического ожидания (генеральной средней) в виде или Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 47

ПРАКТИКУМ Базовый пример 6: По и в ПРИЛОЖЕНИИ 3 на стр. 464 определить значение : , , , Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 48
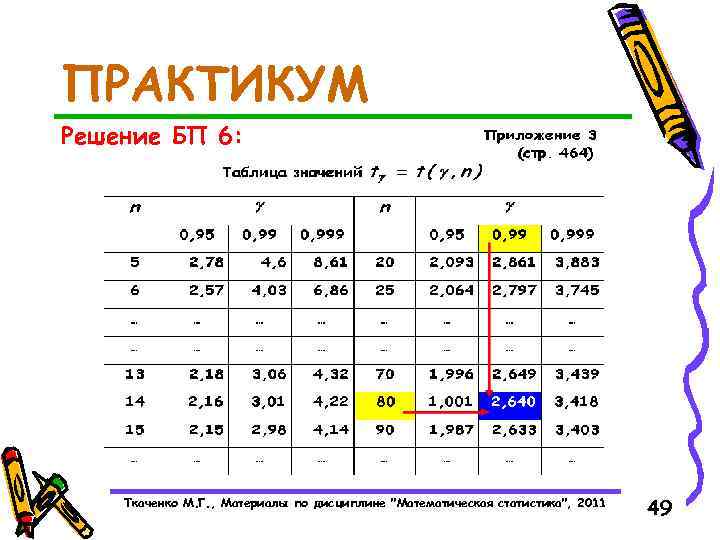
ПРАКТИКУМ Решение БП 6: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 49

ПРАКТИКУМ Решение БП 6 (продолжение): , , , Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 50

ПРАКТИКУМ Базовый пример 7: Средняя урожайность пшеницы на 16 опытных участках области составила 25 ц/га, а «исправленное среднее квадратическое отклонение» равно 2 ц/га. Найти с надежностью 0, 99 границы доверительного интервала для оценки генеральной средней. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 51

ПРАКТИКУМ Решение БП 7: 1. объем выборки 2. средняя выборочная 3. «исправленное» среднее квадратическое отклонение 4. надежность (доверительная вероятность) Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 52

ПРАКТИКУМ Решение БП 7 (продолжение): • • по значениям и в ПРИЛОЖЕНИИ 3 на стр. 464 определяем вычисляем точность оценки по выборочным данным Доверительный интервал для генеральной средней или Окончательно получаем доверительный интервал: или Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 53

Интервальные оценки параметров распределения l Интервальная оценка для генерального среднего квадратического отклонения нормального распределения Доверительный интервал: При , с учетом доверительный интервал: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 54

Интервальные оценки параметров распределения Порядок построения доверительного интервала для генерального среднего квадратического отклонения Из условия задачи 1. определить объем выборки 2. определить или вычислить по формуле «исправленное» среднее квадратическое отклонение 3. определить надежность (доверительную вероятность) или вычислить ее по уровню значимости l по значениям и найти , пользуясь таблицей значений в ПРИЛОЖЕНИИ 4 на стр. 464 l вычислить доверительные границы и записать доверительный интервал для генерального среднего квадратического отклонения в виде или Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 55

ПРАКТИКУМ Базовый пример 8: По и в ПРИЛОЖЕНИИ 4 на стр. 464 определить значение. , , , Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 56
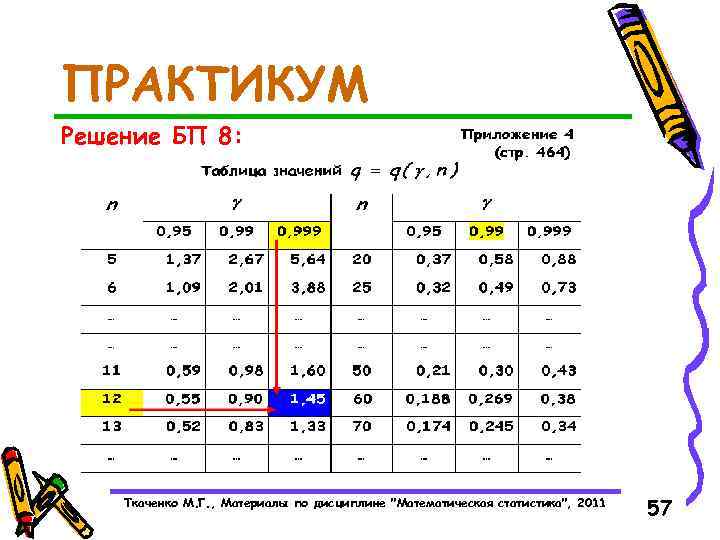
ПРАКТИКУМ Решение БП 8: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 57

ПРАКТИКУМ Решение БП 8 (продолжение): , , , Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 58

ПРАКТИКУМ Базовый пример 9: По результатам контроля 25 деталей вычислено выборочное среднее квадратическое отклонение, которое оказалось равно 5 мм. В предположении, что ошибка изготовления деталей распределена нормально, определить с надежностью 0, 999 доверительный интервал для генерального среднего квадратического отклонения. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 59

ПРАКТИКУМ Решение БП 9: 1. объем выборки 2. «исправленное» среднее квадратическое отклонение 3. надежность (доверительная вероятность) Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 60

ПРАКТИКУМ Решение БП 9 (продолжение): • • • по значениям и в ПРИЛОЖЕНИИ 4 на стр. 464 определяем вычисляем доверительные границы и записываем доверительный интервал для генерального среднего квадратического отклонения в виде или окончательно получаем доверительный интервал: или Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 61

Интервальные оценки параметров распределения l Интервальная оценка для генеральной доли (вероятности) биномиального распределения Доверительный интервал при : , где При , доверительный интервал: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 62

Интервальные оценки параметров распределения Из 1. 2. 3. l l Порядок построения доверительного интервала для генеральной доли условия задачи определить выборочную долю или вычислить ее по формуле, определив объем выборки и число объектов выборки обладающих изучаемым признаком определить надежность (доверительную вероятность) или вычислить ее по уровню значимости определить значение функции (интеграла вероятностей) Лапласа по найденному в п. 3 значению функции по таблице значений функции Лапласа в ПРИЛОЖЕНИИ 2 на стр. 462463 найти аргумент найти точность оценки по выборочным данным и записать доверительный интервал для генеральной доли в виде при или, вычислив доверительные границы , , записать доверительный интервал в виде при Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 63

ПРАКТИКУМ Базовый пример 10: При испытании зерна на всхожесть из 400 зерен проросло 384. С надежностью 0, 98 определить доверительный интервал для генеральной доли. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 64

ПРАКТИКУМ Решение БП 10: 1. Выборочная доля 2. Надежность (доверительная вероятность) 3. Определяем значение функции (интеграла вероятностей) Лапласа Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 65

ПРАКТИКУМ Решение БП 10 (продолжение): • • по значению функции в ПРИЛОЖЕНИИ 2 на стр. 462 -463 определяем аргумент вычисляем точность оценки по выборочным данным Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 66

ПРАКТИКУМ Решение БП 10 (продолжение): • доверительный интервал для генеральной доли или • Окончательно получаем доверительный интервал: или Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 67

Точечные оценки параметров распределения l Вычисление объема выборки Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 68

ПРАКТИКУМ Базовый пример 11: Обследуется выработка 1000 рабочих цеха в отчетном году по сравнению с предыдущим по схеме собственно-случайной выборки. Определить объем выборки, при котором с надежностью (доверительной вероятностью) 0, 9973 отклонение средней выработки рабочих в выборке от средней выработки всех рабочих цеха не превзойдет 1% (по абсолютной величине), если известно, что выборочная дисперсия равна 87, 48. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 69

ПРАКТИКУМ Решение БП 11: • • • Для определения объема выборки в условии задачи дана точность оценки и объем генеральной (изучаемой) совокупности По надежности определяем значение функции (интеграла вероятностей) Лапласа По значению функции в ПРИЛОЖЕНИИ 2 на стр. 462 -463 определяем аргумент Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 70

ПРАКТИКУМ Решение БП 11 (продолжение): • • В качестве неизвестного значения для определения объема выборки возьмем его состоятельную оценку Найдем объем повторной выборки: • Найдем объем бесповторной выборки: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 71

ПРАКТИКУМ Базовый пример 12: Из партии в 2000 деталей для проверки по схеме собственно-случайной бесповторной выборки было отобрано 200 деталей, среди которых оказалось 184 стандартных. Определить число деталей, которые надо отобрать в выборку, чтобы с вероятностью 0, 95 доля нестандартных деталей в выборке отличалась от генеральной доли не более, чем на 0, 04 (по абсолютной величине). Найти то же число, если о доле нестандартных деталей, даже приблизительно ничего неизвестно. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 72

ПРАКТИКУМ Решение БП 12: • • • Для определения объема выборки в условии задачи дана точность оценки и объем генеральной (изучаемой) совокупности По надежности определяем значение функции (интеграла вероятностей) Лапласа По значению функции в ПРИЛОЖЕНИИ 2 на стр. 462 -463 определяем аргумент Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 73

ПРАКТИКУМ Решение БП 12 (продолжение): • В качестве неизвестного значения генеральной доли нестандартных деталей возьмем ее состоятельную оценку (долю нестандартных деталей в выборке), которую найдем из данных задачи: • Найдем объем бесповторной выборки: Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 74

Вычисление численных характеристик вариационного ряда l l l РЕЗЮМЕ 2 При изучении качественного или количественного признака, характеризующего совокупность однородных объектов, не всегда имеется возможность обследовать каждый объект изучаемой совокупности. О параметрах генеральных совокупностей делаются выводы по выборкам из них. Выборка должна быть репрезентативной. Основная задача теории оценивания – выбор оценки, позволяющей получить хорошее приближение оцениваемого параметра. Для оцениваемого параметра можно найти как точечные, так и интервальные оценки. Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 75

СПАСИБО ЗА ВНИМАНИЕ!!! Ткаченко М. Г. , Материалы по дисциплине "Математическая статистика", 2011 76
МС2011 тема 2 с практикой NEW.ppt