План 1 Стаціонарний рух ідеальної рідини Рівняння Бернуллі

План: 1. Стаціонарний рух ідеальної рідини. Рівняння Бернуллі. Трубка Піто. 2. Гідродинаміка в’язкої рідини. Коефіцієнт в’язкості. Течія по трубі. 3. Формула Стокса. Формула Пуазейля. Число Рейнольдcа.

ЕЛЕМЕНТИ КІНЕМАТИКИ СУЦІЛЬНИХ СЕРЕДОВИЩ Рух рідин називають течією, а сукупність частинок рухомої рідини – потоком. Течію рідини називають усталеною, або стаціонарною, якщо швидкість рідини у кожній точці простору, який займає рідина, не змінюється з часом. Потік можна зобразити за допомогою ліній течії

Лінії течії – це лінії, дотична до яких збігається з вектором швидкості частинки рідини у даній точці. Чим густішими є лінії течії, тим більшу швидкість має рідина. Картина ліній течії при стаціонарній течії не змінюється і лінії течії у цьому випадку збігаються з траєкторіями частинок. Якщо через усі точки невеликого замкнутого контуру провести лінії течії, то утвориться поверхня, яку називають трубкою течії. Лінії течії та швидкості частинок рухомої рідини

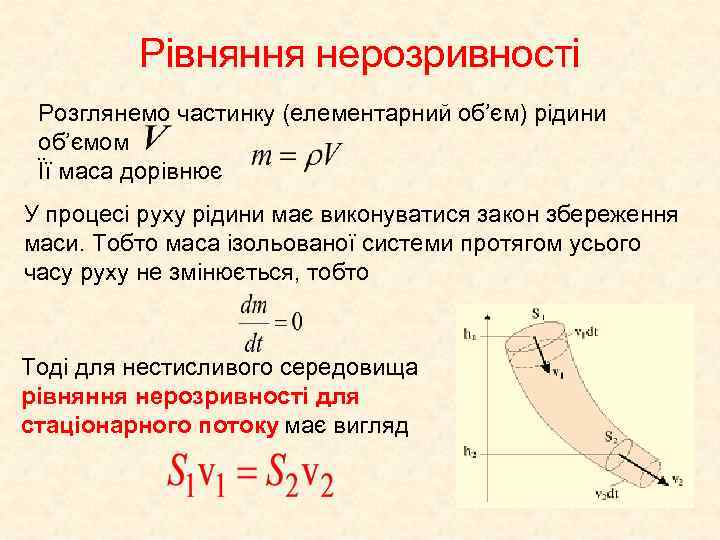
Рівняння нерозривності Розглянемо частинку (елементарний об’єм) рідини об’ємом Її маса дорівнює У процесі руху рідини має виконуватися закон збереження маси. Тобто маса ізольованої системи протягом усього часу руху не змінюється, тобто Тоді для нестисливого середовища рівняння нерозривності для стаціонарного потоку має вигляд

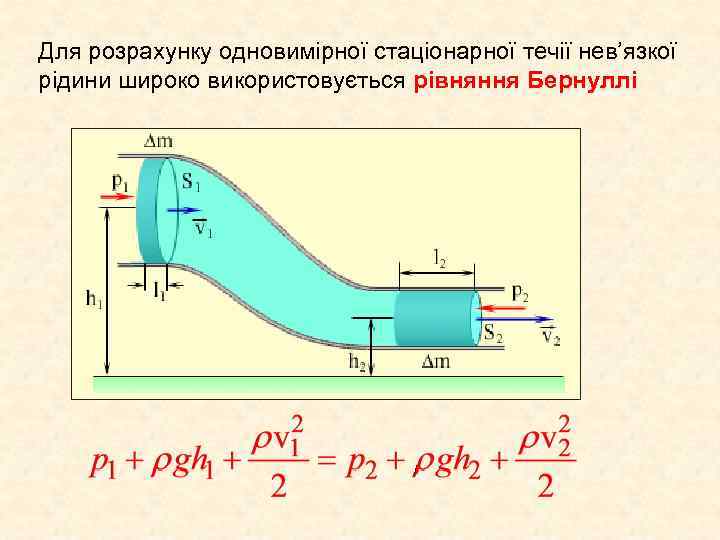
Для розрахунку одновимірної стаціонарної течії нев’язкої рідини широко використовується рівняння Бернуллі

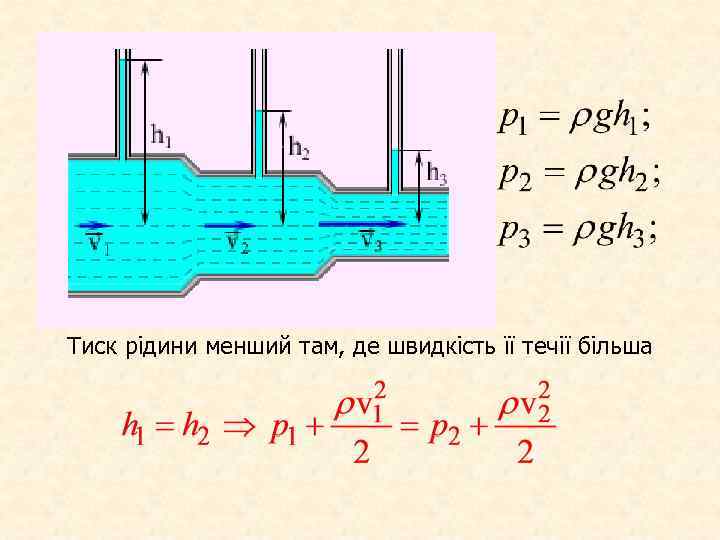
Тиск рідини менший там, де швидкість її течії більша

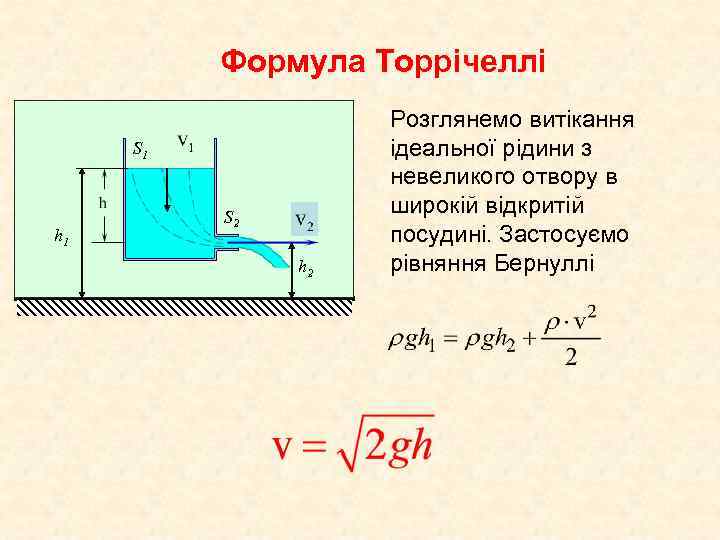
Формула Торрічеллі S 1 h 1 S 2 h 2 Розглянемо витікання ідеальної рідини з невеликого отвору в широкій відкритій посудині. Застосуємо рівняння Бернуллі

В’язкість - це внутрішнє тертя, яке мають всі реальні рідини і гази. Ламінарною течією називають течію без перемішування шарів рідини. При збільшенні швидкості течії ламінарний рух переходить у турбулентний, при якому відбувається перемішування шарів потоку. Для створення та підтримання сталою течію рідини в трубі, потрібно створити і підтримувати різницю тисків між кінцями труби. Оскільки при встановленому русі рідина рухається без прискорення, необхідність дії сил тиску вказує на те, що ці сили врівноважуються силами опору руху рідини (внутрішнього тертя).

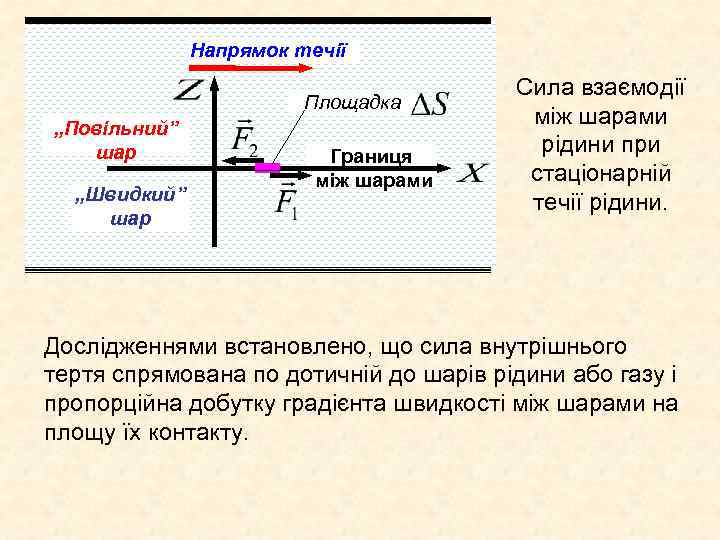
Напрямок течії Площадка „Повільний” шар „Швидкий” шар Границя між шарами Сила взаємодії між шарами рідини при стаціонарній течії рідини. Дослідженнями встановлено, що сила внутрішнього тертя спрямована по дотичній до шарів рідини або газу і пропорційна добутку градієнта швидкості між шарами на площу їх контакту.

Модуль сили внутрішнього тертя для ламінарної течії визначається рівнянням Ньютона - динамічний коефіцієнт в’язкості, який залежить від природи і стану (наприклад, температури) рідини. Відзначимо, що при ламінарній течії швидкість змінюється з відстанню від осі труби за параболічним законом. Профіль швидкостей при ламінарній (а) та турбулентній (б) течії в циліндричній трубі а б

Формула Пуазейля для розрахунку спаду тиску рідини у потоці Формула Пуазейля дослідного визначення коефіцієнта в'язкості рідини

Елементи теорії подібності Теорія подібності - вчення про умови подібності фізичних явищ. Ця теорія ґрунтується на вченні про розмірності фізичних величин (аналіз розмірностей) і є основою фізичного моделювання. Фізичне моделювання - вид моделювання, який полягає в заміні вивчення деякого об'єкта або явища експериментальним дослідженням його моделі, яка має таку саму фізичну природу. Предметом теорії подібності є встановлення критеріїв подібності різних фізичних явищ і вивчення за допомогою цих критеріїв властивостей самих явищ. Основними критеріями подібності гідрогазодинамічних процесів є число Рейнольдса.

Рейнольдсу вдалося знайти безрозмірне число, що описує характер потоку в'язкої рідини. Сам вчений одержав його експериментально, провівши виснажливу серію дослідів з різними рідинами, однак незабаром було показано, що його можна вивести і теоретично з законів механіки Ньютона і рівнянь класичної гідродинаміки. Це число - число Рейнольдса характеризує потік і дорівнює Режим течії рідини визначається критичним числом Рейнольдса. Ламінарна течія рідини Турбулентна течія

ФОРМУЛА СТОКСА Стокс встановив, що за невеликих швидкостей модуль сили опору руху тіла в рідинах визначається формулою Сила опору руху в рідинах невеличких кульок при невеликих швидкостях (ламінарна течія) Формула Стокса є справедливою за умови, що відстань від тіла до стінок посудини набагато більша за розміри тіла.