Placing Controllers in a System Overview of

Placing Controllers in a System

Overview of Class So Far… l l General Introduction Deregulation Traditional approaches to control Static devices

Type of problems l l l Steady State Transient Stability Inter-Area Oscillations Subsynchronous Resonance Voltage Stability

Introduction to FACTS l Detailed analysis of devices y Thyristor controlled inductor y SVC y Statcom y TCSC

System Modeling l Simplified models for use in system simulations and analysis y Statcom y TCSC (see Reference [1]) y UPFC

Set up system equations to include FACTS devices l l l Get block diagrams or differential equations for device Define device states Define device inputs Express device model in terms of existing system states & device states Augment system equations

Use these devices to fix system problems!

OK, Say you work at an ISO & are in charge of ensuring system reliability. You've had 5 major blackouts in the last 3 years that have involved the propagation of problems from one part of the system to another. The utility members are convinced that the addition of a FACTS device or two will solve the problems & they even agree to pay!

Now what do you do? . . . l Brainstorming Activity: y What things do you need to worry about? y Break into groups of 2 or 3 y Take 3 minutes & write down as many things as you can y No criticism allowed, Go for variety, Go for quantity not quality

Questions: l l Where do I put it? What should it do? Controller Location Controller Function

Things to consider: l l More than one problem More than one system condition More than one mode More than one tool

Problems l Steady State y Insure operating point is within acceptable limits l Interarea Oscillations y Damp eigenvalues

l Transient Stability y Provide sufficient synchronizing and damping torque l Subsynchronous Resonance y Avoid resonance frequencies l Voltage Stability y Stabilize eigenvalues and avoid bifurcations

Interarea Oscillation Mitigation l Analysis Tools (Mostly Linear) y Controllability and Observability y Participations y Sensitivities y Power Oscillation Flows

Linearized System x’ = Ax + Bu y = Cx + Du l l Eigenvalues are li, i = 1, nstates Right Eigenvectors ri , R is matrix of ri's Left Eigenvectors (rows) li, L is matrix of li's L = R -1

Perform variable transformation to Jordan Form l l x = Rz (Inverse transform z = Lx) Substituting into system equations. . . Rz’ = AR z + B u y = CR z + Du

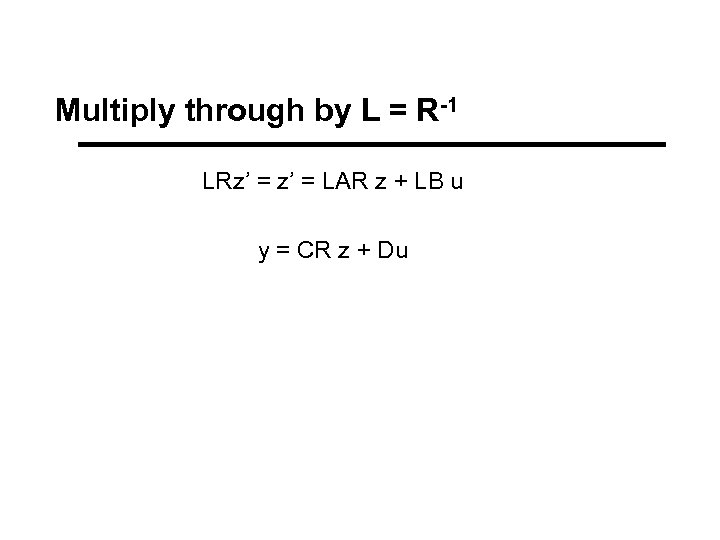Multiply through by L = R-1 LRz’ = LAR z + LB u y = CR z + Du

Controllability and Observability l Modal controllability matrix = LB y tells how strongly connected the inputs (u's) are to each of the modes l Modal observability matrix = CR y tells how well we can measure or "see" each mode in the outputs (y's)

Participations l l Connection strengths between modes and states General participation y pi hk = ri h lhk y link between ith (obs. ) & kth (con. ) states through mode h l Participation Factors y pi h = r i h l h i y link between mode h & state i

Eigenvalue Sensitivities li’ = dli/dp l l l p some parameter of the system Tells how easily we can move an eigenvalue by changing a parameter In general, li' = li A' ri

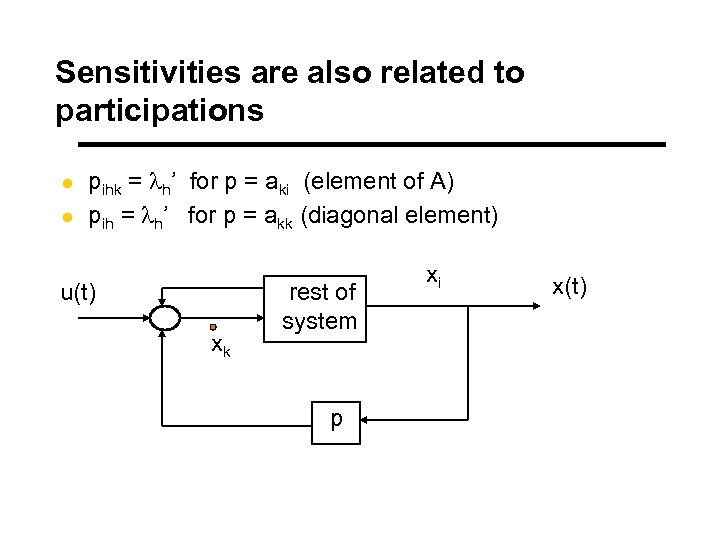Sensitivities are also related to participations l l pihk = lh’ for p = aki (element of A) pih = lh’ for p = akk (diagonal element) u(t) xk rest of system p xi x(t)

Sensitivity with Controllers l The "Hybrid System"

The Power System x’ = Ax + Bu y = Cx l l assume no direct connection between y & y 2 The controller transfer function F(s, p) is the only place p shows up

Sensitivity for Hybrid System l l li’ = dli/dp = li B {d/dp [F(s, p)]|s=li } C ri related to the controllability and observability measures and to the controller transfer function (see Reference [5])

Uses of Sensitivities l l Location of controllers Magnitude of l’ tells the displacement of the eigenvalue if gain is equal to 1 Large magnitude indicates controller is a good candidate for improving a mode Phase l’ of gives the direction of the eigenvalue's displacement in the imaginary plane

Introduce devices likely to influence these characteristics l Simulations and Trial & Error

Tuning of a controller. . . l l Adjust the phase compensation of the controller so that l’ has a phase of 180 degrees with controller in place Adjust the gain of the controller to achieve the desired amount of damping

Power Oscillation Flows l Map where oscillations caused by a single eigenvalue appear in the system n x(t) = S ck elkt rk k=1 l ck is the initial condition in Jordan Space

l The idea is to choose ck's so that only one mode is perturbed, i. e. ci = 1 and ck= 0 for all k not equal i then l x(t) = ri elit this solution can then be propagated through the system equations to find the power flow on key lines (or some other variable for that matter)

Placing a FACTS device using participations, sensitivities, etc. l l Simple & Fast Detailed & More Accurate

Transient Stability and FACTS l l Usually concerned with providing adequate damping and synchronizing torque Often design using linear techniques and test with the nonlinear system

Nonlinear Methods l l Normal forms of vector fields for extending the linear concepts to the nonlinear regions. Second-order oscillations, participations, controllability & observability

Energy Methods l l Lyapunov-based methods for determining stability indices Tracking of energy exchanges during a disturbance

Control Strategy l Determine weak points in system y Poorly damped oscillations y Lack of synchronizing torque y Large power swings y Large energy exchanges y Short critical clearing times y Multi-machine instabilities

References [1] Paserba, J. J. , N. W. Miller, E. V. Larsen, and R. J. Piwko "A Thyristor Controlled Series Compensation Model for Power System Stability Analysis" IEEE Trans. on Power Delivery, Vol. 10? , (July 1994): 1471 -1478. [2] Chan, S. M. "Modal Controllability and Observability of Power. System Models" International Journal of Electric Power and Energy Systems, Vol. 6, No. 2, (April 1994): 83 -89. [3] Rouco, L. , and F. L. Pagola "An Eigenvalue Sensitivity Approach to Location and Controller Design of Controllable Series Capacitors for Damping Power System Oscillations" IEEE-PES 1997 Winter Power Meeting, Paper No. PE-547 PWRS-0 -01 -1997.

[4] Ooi, B. T. , M. Kazerani, R. Marceau, Z. Wolanski, F. D. Galiana, D. Mc. Gillis, and G. Joos "Mid-Point SIting of FACTS Devices in Transimssion Lines" IEEE-PES 1997 Winter Power Meeting, Paper No. PE-292 -PWRD-0 -01 -1997. [5] Pagola, F. L. , I. J. Perez-Arriaga, and G. C. Verghese "On Sensitivities, Residues, and Participations: Application to Oscillatory Stability Analysis and Control" IEEE Trans. on Power Systems, Vol. 4, No. 2, (February 1989): 278 -285. [6] Messina, A. R. , J. M. Ramirez, and J. M. Canedo C. "An Investigation on the use of Power Systme Stabilizers for Damping Inter-Area Oscillations in Longitudinal Power Systems" IEEE-PES 1997 Winter Power Meeting, Paper No. PE-492 -PWRS-0 -01 -1997. [7] Zhou, E. Z. "Power Oscillation Flow Study of Electric Power Systems" International Journal of Electric Power and Energy Systems, Vol. 17, No. 2, (1995): 143 -150.