ef98e5a45a2f76278feea742e6d3f480.ppt
- Количество слайдов: 64

PKCS (Public-key cryptography standards) Códigos y Criptografía Francisco Rodríguez Henríquez
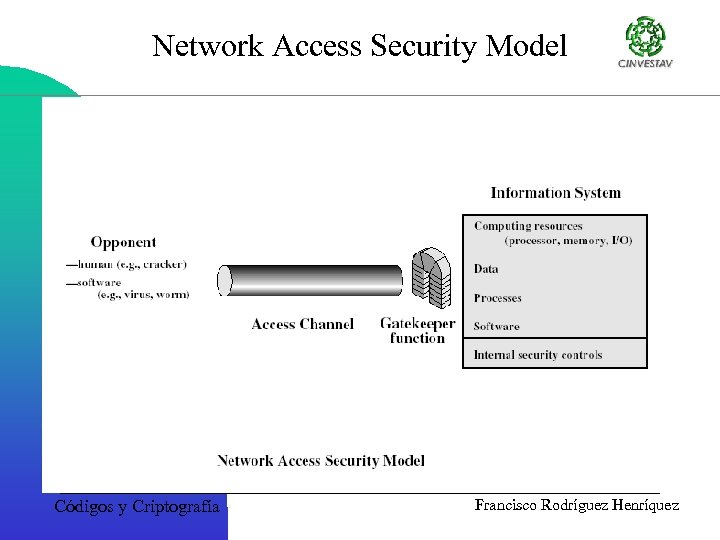
Network Access Security Model Códigos y Criptografía Francisco Rodríguez Henríquez

Security Levels • Confidentiality – Protection from disclosure to unauthorized persons • Integrity – Maintaining data consistency • Authentication – Assurance of identity of person or originator of data • Non-repudiation – Originator of communications can't deny it later • Authorization – Identity combined with an access policy grants the rights to perform some action Códigos y Criptografía Francisco Rodríguez Henríquez

Security Building Blocks • Encryption provides – confidentiality, can provide authentication and integrity protection • Checksums/hash algorithms provide – integrity protection, can provide authentication • Digital signatures provide – authentication, integrity protection, and nonrepudiation Códigos y Criptografía Francisco Rodríguez Henríquez

Keys • Symetric Keys – Both parties share the same secret key – A major problem is securely distributing the key – DES - 56 bit key considered unsafe for financial purposes since 1998 – 3 DES uses three DES keys Códigos y Criptografía Francisco Rodríguez Henríquez

Keys • Public/Private keys – One key is the mathematical inverse of the other – Private keys are known only to the owner – Public key are stored in public servers, usually in a X. 509 certificate. – RSA (patent expires Sept 2000), Diffie. Hellman, DSA Códigos y Criptografía Francisco Rodríguez Henríquez
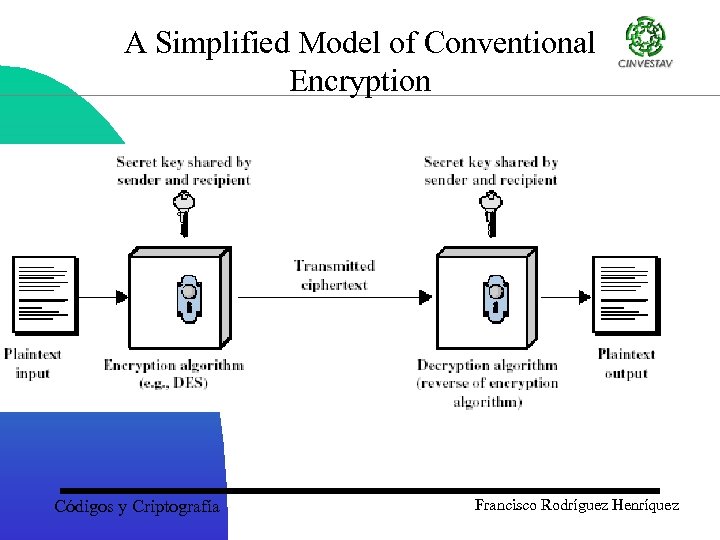
A Simplified Model of Conventional Encryption Códigos y Criptografía Francisco Rodríguez Henríquez
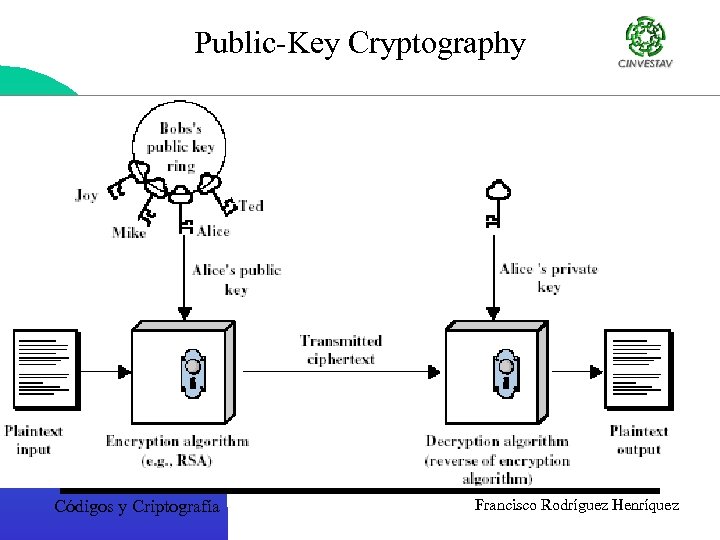
Public-Key Cryptography Códigos y Criptografía Francisco Rodríguez Henríquez
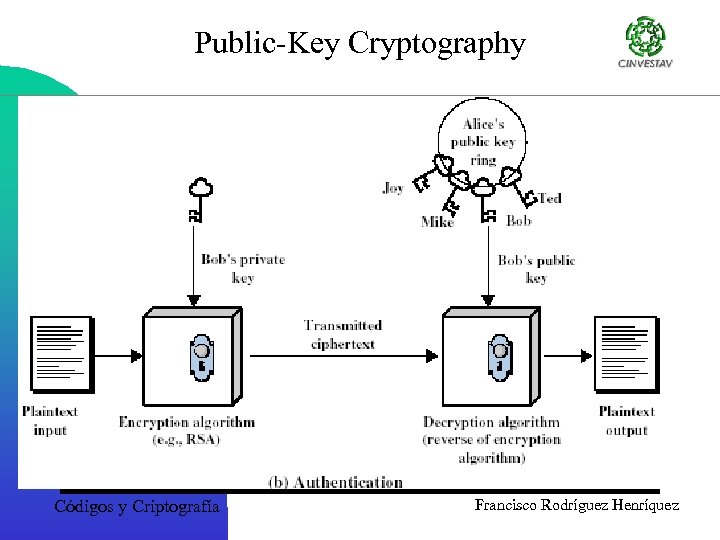
Public-Key Cryptography Códigos y Criptografía Francisco Rodríguez Henríquez

Message Digest • A message digest, also known as a one-way hash function, is a fixed length computionally unique identifier corresponding to a set of data. That is, each unit of data (a file, a buffer, etc. ) will map to a particular short block, called a message digest. It is not random: digesting the same unit of data with the same digest algorithm will always produce the same short block. • A good message digest algorithm possesses the following qualities – The algorithm accepts any input data length. – The algorithm produces a fixed length output for any input data. – The digest does not reveal anything about the input that was used to generate it. – It is computationally infeasible to produce data that has a specific digest. – It is computationally infeasible to produce two different unit of data that produce the same digest. Francisco Rodríguez Henríquez Códigos y Criptografía

Hash Algorithms • Reduce variable-length input to fixedlength (128 or 160 bit) output • Requirements – Can't deduce input from output – Can't generate a given output – Can't find two inputs which produce the same output Códigos y Criptografía Francisco Rodríguez Henríquez

Hash Algorithms • Used to – Produce fixed-length fingerprint of arbitrarylength data – Produce data checksums to enable detection of modifications – Distill passwords down to fixed-length encryption keys • Also called message digests or fingerprints Códigos y Criptografía Francisco Rodríguez Henríquez

Message Authentication Code MAC • Hash algorithm + key to make hash value dependant on the key • Most common form is HMAC (hash MAC) – hash( key, data )) • Key affects both start and end of hashing process • Naming: hash + key = HMAC-hash – MD 5 1 HMAC-MD 5 – SHA-1 1 HMAC-SHA (recommended) Códigos y Criptografía Francisco Rodríguez Henríquez
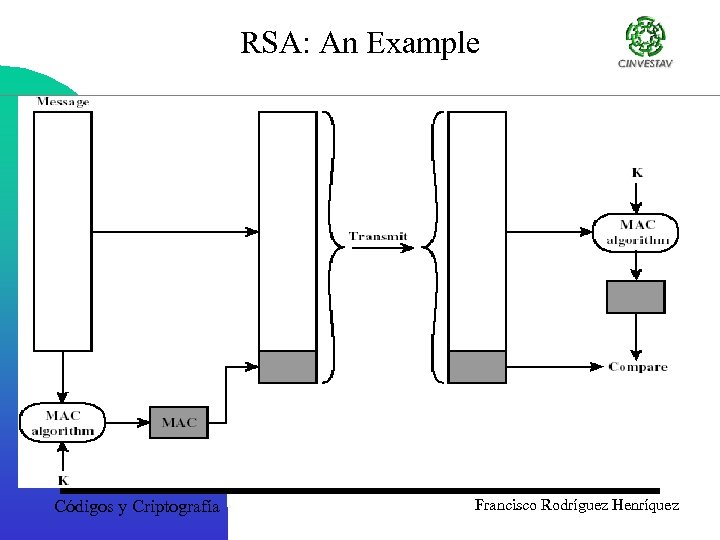
RSA: An Example Códigos y Criptografía Francisco Rodríguez Henríquez

Digital Signatures • Combines a hash with a digital signature algorithm • To sign – hash the data – encrypt the hash with the sender's private key – send data signer’s name and signature • To verify – hash the data – decrypt the signature with the sender's public key – the result of which should match the hash Códigos y Criptografía Francisco Rodríguez Henríquez

Digital Signatures • A data string associating a message with an originating entity – Signature generation algorithm – Signature verification algorithm – Signature scheme • Used for authentication, integrity, and nonrepudiation • Public key certification is one of the most significant applications Códigos y Criptografía Francisco Rodríguez Henríquez
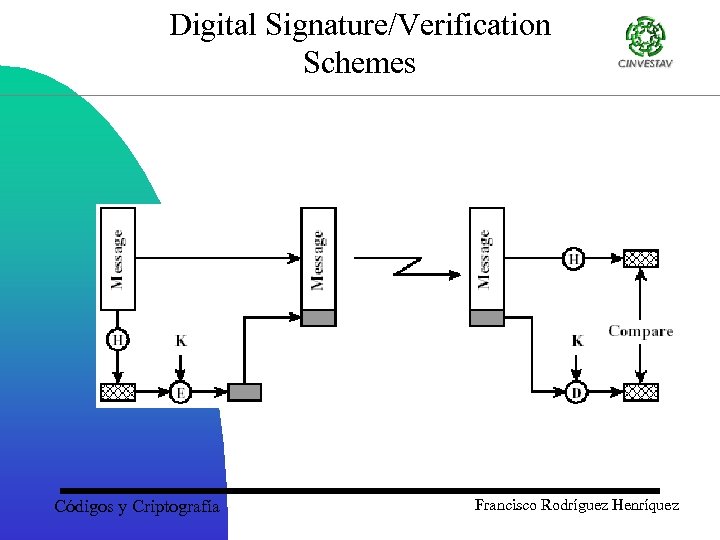
Digital Signature/Verification Schemes Códigos y Criptografía Francisco Rodríguez Henríquez
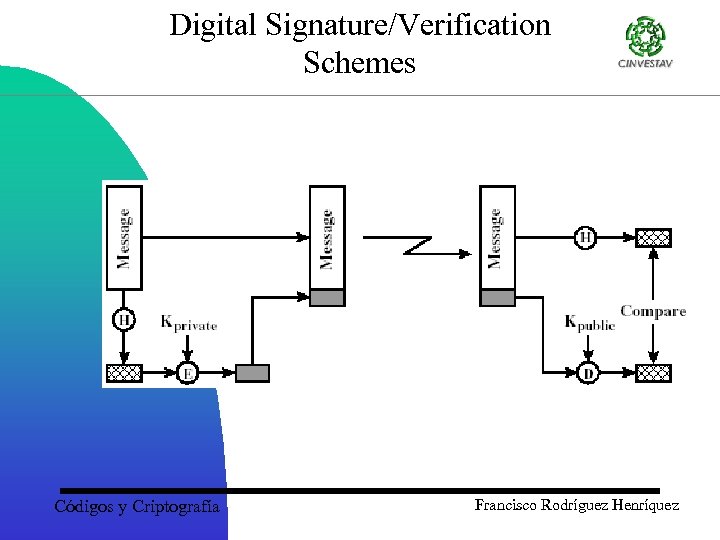
Digital Signature/Verification Schemes Códigos y Criptografía Francisco Rodríguez Henríquez
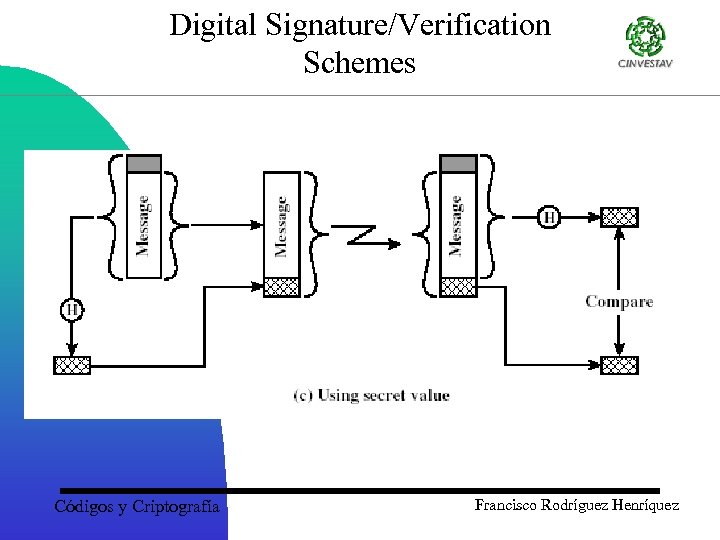
Digital Signature/Verification Schemes Códigos y Criptografía Francisco Rodríguez Henríquez
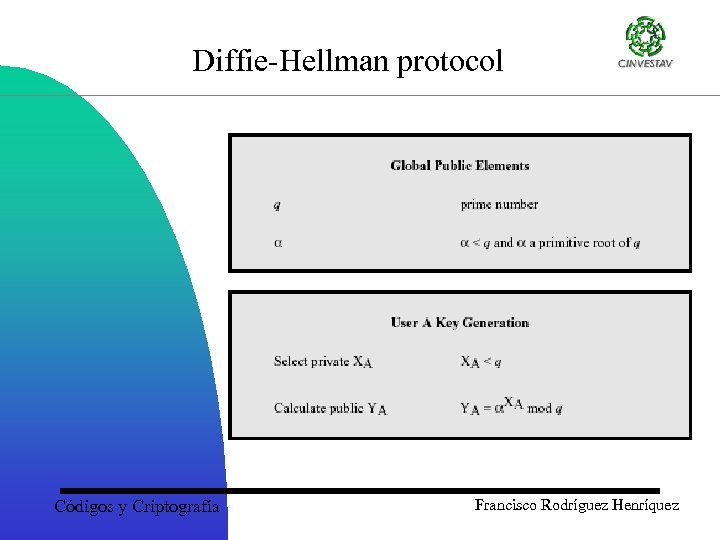
Diffie-Hellman protocol Códigos y Criptografía Francisco Rodríguez Henríquez

Diffie-Hellman protocol Códigos y Criptografía Francisco Rodríguez Henríquez
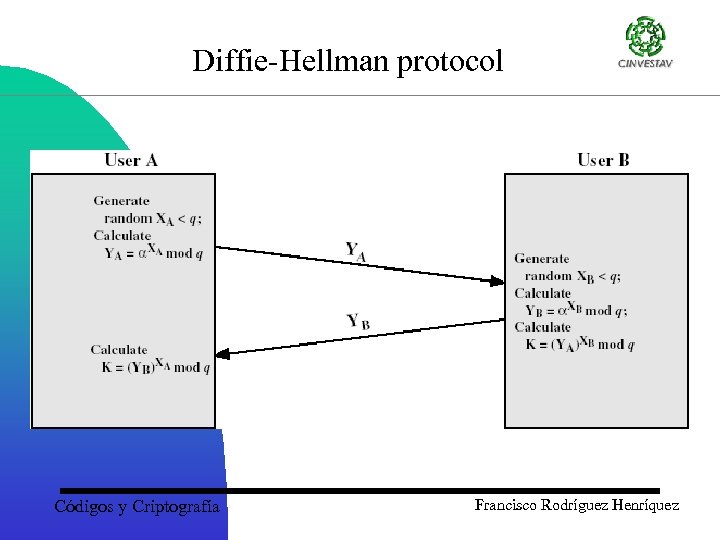
Diffie-Hellman protocol Códigos y Criptografía Francisco Rodríguez Henríquez
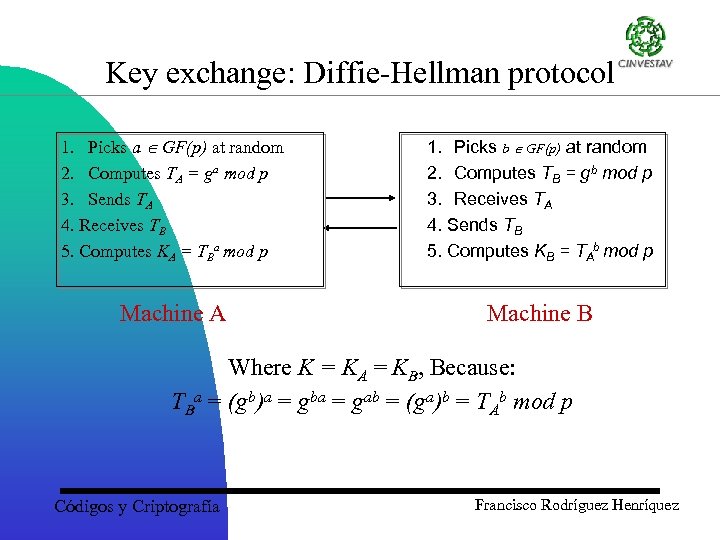
Key exchange: Diffie-Hellman protocol 1. Picks a GF(p) at random 2. Computes TA = ga mod p 3. Sends TA 4. Receives TB 5. Computes KA = TBa mod p 1. Picks b GF(p) at random 2. Computes TB = gb mod p 3. Receives TA 4. Sends TB 5. Computes KB = TAb mod p Machine A Machine B Where K = KA = KB, Because: TBa = (gb)a = gba = gab = (ga)b = TAb mod p Códigos y Criptografía Francisco Rodríguez Henríquez

Mensaje para Anita en La Jornada Querida Anita de mi corazón: Quisiera pedirte que nuestro número primo sea 128903289023 y nuestra g 23489. Te quiere Betito. Códigos y Criptografía Francisco Rodríguez Henríquez

Middle-person attack. • Consider the following scenario: Anita Middleperson Betito ga = 8389 gx = 5876 gb = 9267 8389 5876 9267 Shared key KAX: Shared key KBX 5876 a = 8389 x 9267 x = 5876 b • After this exchange, the middle-person attacker simply decrypts any messages sent out by A or B, and then reads any possibly modifies them before re-encrypting with the appropriate key and transmitting them to the correct party. • Middle-person attack is possible due to the fact that DHC does not authenticate the participants. Possible solutions are digital signatures and other protocol variants. Códigos y Criptografía Francisco Rodríguez Henríquez
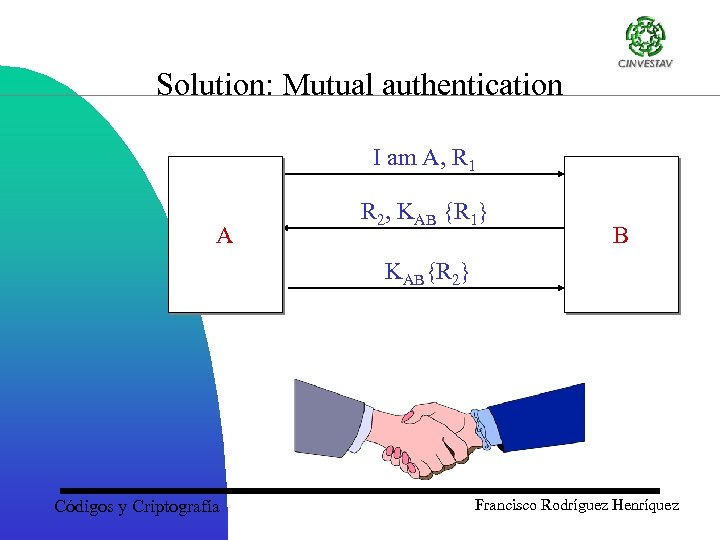
Solution: Mutual authentication I am A, R 1 A R 2, KAB {R 1} B KAB{R 2} Códigos y Criptografía Francisco Rodríguez Henríquez
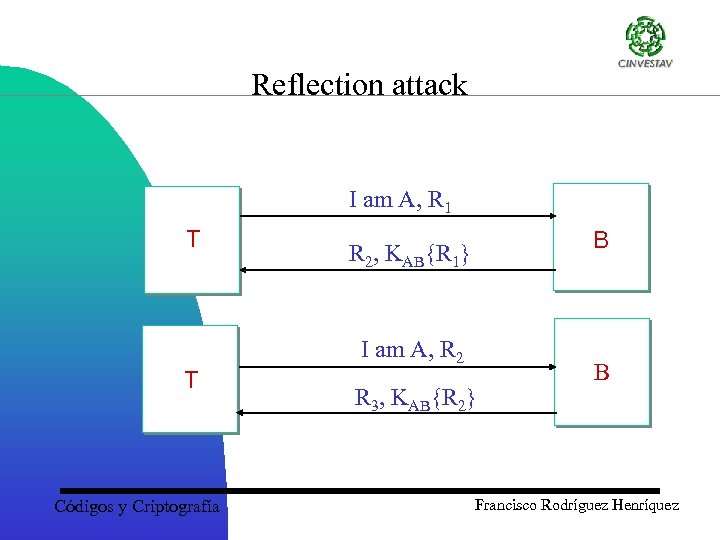
Reflection attack I am A, R 1 T B R 2, KAB{R 1} I am A, R 2 T Códigos y Criptografía R 3, KAB{R 2} B Francisco Rodríguez Henríquez
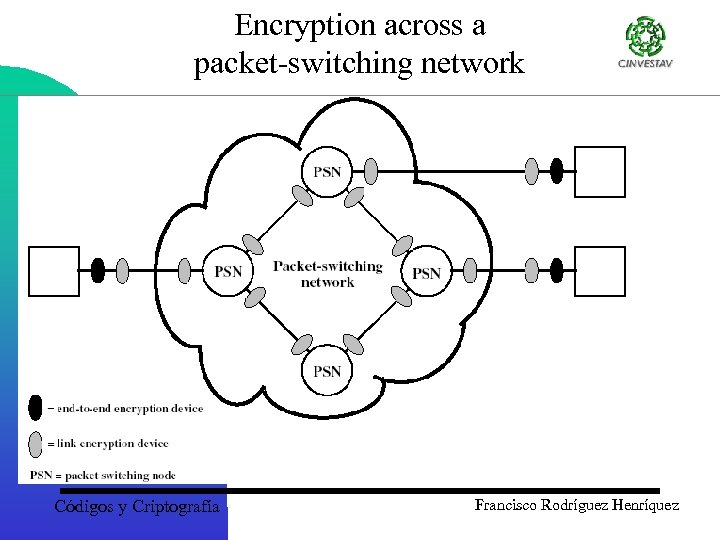
Encryption across a packet-switching network Códigos y Criptografía Francisco Rodríguez Henríquez

Elements of PKI • Certificate Authorities (CA) – Open. SSL, Netscape, Verisign, Entrust, RSA Keon • Public/Private Key Pairs - Key management • x. 509 Identity Certificates - Certificate management • LDAP servers Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS • • • Public-key cryptography standards (PKCS) Owned by RSA and motivated to promote RSA Created in early 1990’s Numbered from PKCS 1 to PKCS 15 Some along the way have – lost interest – folded into other PKCS – taken over by other standards bodies • Continue to evolve Códigos y Criptografía Francisco Rodríguez Henríquez
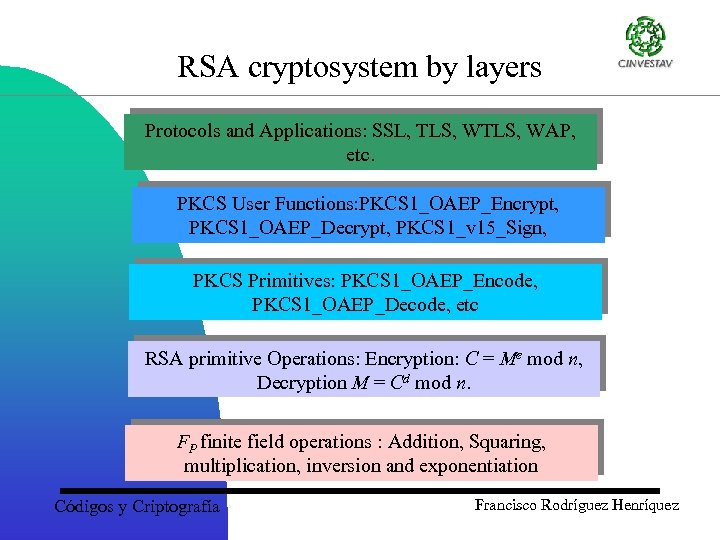
RSA cryptosystem by layers Protocols and Applications: SSL, TLS, WAP, etc. PKCS User Functions: PKCS 1_OAEP_Encrypt, PKCS 1_OAEP_Decrypt, PKCS 1_v 15_Sign, PKCS Primitives: PKCS 1_OAEP_Encode, PKCS 1_OAEP_Decode, etc RSA primitive Operations: Encryption: C = Me mod n, Decryption M = Cd mod n. FP finite field operations : Addition, Squaring, multiplication, inversion and exponentiation Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 • RSA Cryptography Standard Version 2. 0 onwards (1998) RSA Encryption Standard Version 1. 5 (1993) Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 • Specifies how to use the RSA algorithm securely for encryption and signature • Why do we need this? – Padding for encryption – Different schemes for signature Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 • Chosen ciphertext attack based on multiplicative property of RSA • Attacker wishes to decrypt c Choose r, compute c’ = c re mod n Get victim to decrypt c’ giving cd r mod n cd r r-1 mod n = cd mod n • Padding destroys multiplicative property Códigos y Criptografía Francisco Rodríguez Henríquez

RSA: Key Generation Códigos y Criptografía Francisco Rodríguez Henríquez

RSA: Encryption, Decryption Códigos y Criptografía Francisco Rodríguez Henríquez
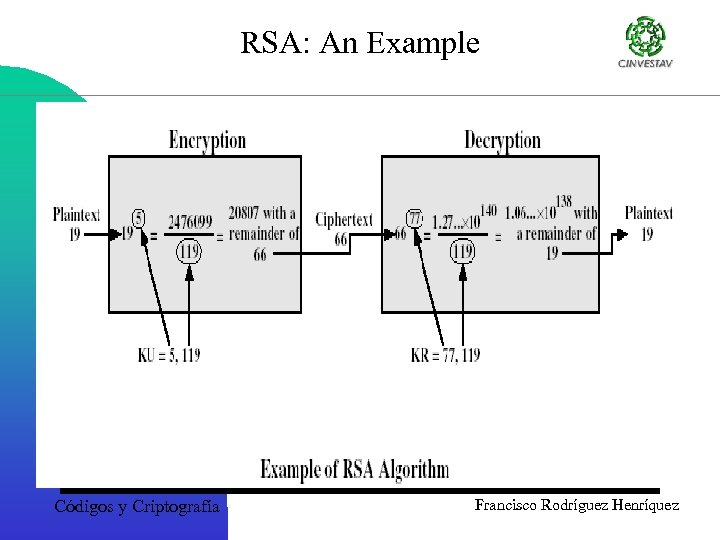
RSA: An Example Códigos y Criptografía Francisco Rodríguez Henríquez

RSA encryption is deterministic We can check whether M is the message of C by C=Me mod n. Attack example: C = (PIN)e mod n, where PIN is 4 -digit number. We can find M by a brute force attack within several 10 seconds. => We need a semantically secure cryptosystem! Semantically secure: For two messages M 0, M 1, and C = Mb 2 mod n, attackers can not guess whether C is encryption of Mb (b=0, 1). An easy way is to pad M with random integer R like M||R, but no security proof! Códigos y Criptografía Francisco Rodríguez Henríquez
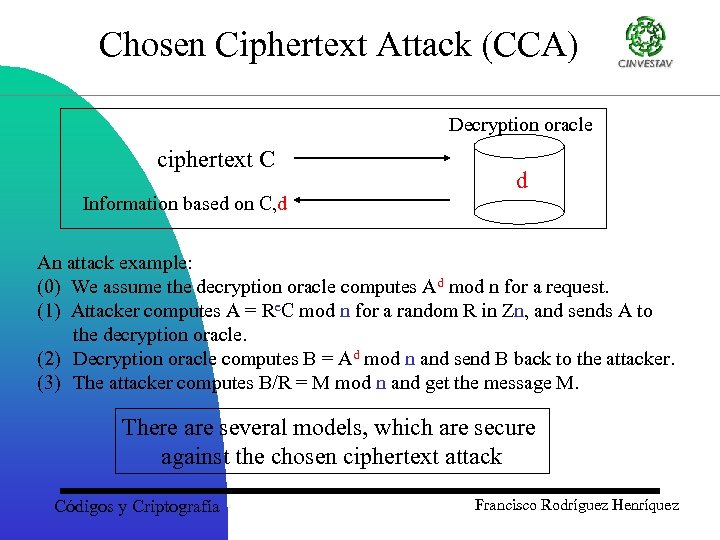
Chosen Ciphertext Attack (CCA) Decryption oracle ciphertext C Information based on C, d d An attack example: (0) We assume the decryption oracle computes Ad mod n for a request. (1) Attacker computes A = Re. C mod n for a random R in Zn, and sends A to the decryption oracle. (2) Decryption oracle computes B = Ad mod n and send B back to the attacker. (3) The attacker computes B/R = M mod n and get the message M. There are several models, which are secure against the chosen ciphertext attack Códigos y Criptografía Francisco Rodríguez Henríquez
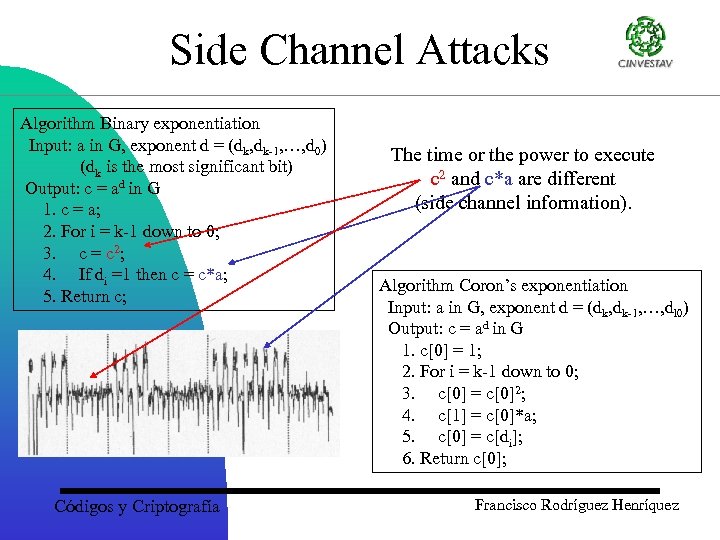
Side Channel Attacks Algorithm Binary exponentiation Input: a in G, exponent d = (dk, dk-1, …, d 0) (dk is the most significant bit) Output: c = ad in G 1. c = a; 2. For i = k-1 down to 0; 3. c = c 2; 4. If di =1 then c = c*a; 5. Return c; Códigos y Criptografía The time or the power to execute c 2 and c*a are different (side channel information). Algorithm Coron’s exponentiation Input: a in G, exponent d = (dk, dk-1, …, dl 0) Output: c = ad in G 1. c[0] = 1; 2. For i = k-1 down to 0; 3. c[0] = c[0]2; 4. c[1] = c[0]*a; 5. c[0] = c[di]; 6. Return c[0]; Francisco Rodríguez Henríquez
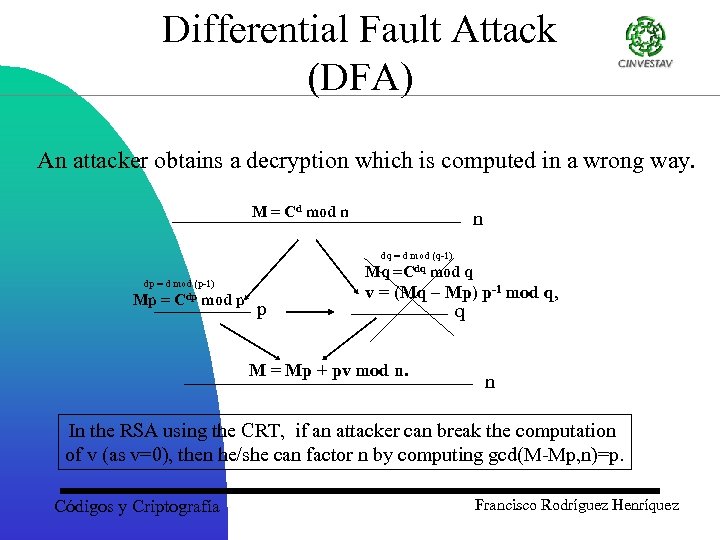
Differential Fault Attack (DFA) An attacker obtains a decryption which is computed in a wrong way. M = Cd mod n n dq = d mod (q-1) Mq =Cdq mod q dp = d mod (p-1) Mp = Cdp mod p p v = (Mq – Mp) p-1 mod q, M = Mp + pv mod n. q n In the RSA using the CRT, if an attacker can break the computation of v (as v=0), then he/she can factor n by computing gcd(M-Mp, n)=p. Códigos y Criptografía Francisco Rodríguez Henríquez

Klima-Rosa attack against PGP dose not encrypt the key file which includes n. Decryption oracle integer X Xd mod n’ d, n’ An attacker can change the public key n to n’ The attacker can obtain Xd mod n’ for changed n’. He/she can recover d by Silver-Pohlig-Hellman algorithm Códigos y Criptografía Francisco Rodríguez Henríquez

Bleichenbacher’s CCA Decryption oracle any integer C mod n Cd ∈ PKCS-format or not d PKCS-Format for a message m most significant byte 00 02 random padding 00 least significant byte message m at least 8 bytes Theorem (Bleichenbacher): Let n be a 1024 -bit RSA modus. For a given C, the value Cd mod n can be computed by about 220 accesses to the decryption oracle, where d is the secret key. Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 • Version 1. 5, 1993 – Encryption padding was found defective in 1998 by Bleichenbacher – Possible to generate valid ciphertext without knowing corresponding plaintext with reasonable probability of success (chosen ciphertext) Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 • • • Uses Optimal asymmetric encryption protocol (OAEP) by Bellare-Rogoway 1994 – provably secure in the random oracle model. – Informally, if hash functions are truly random, then an adversary who can recover such a message must be able to break RSA – plaintext-awareness: to construct a valid OAEP encoded message, an adversary must know the original plaintext PKCS 1 version 1. 5 padding continues to be allowed for backward compatibility Accommodation for multi-prime RSA – Speed up private key operations Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 • • • Cryptographic primitives Cryptographic scheme – Encryption scheme – Signature scheme • Signature with appendix: supported • Signature with message recovery: not supported Encoding and decoding – Converting an integer message into an octet string for use in encryption or signature scheme and vice versa Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 • Cryptographic primitives • Encrypt RSAEP((n, e), m) • Decrypt RSADP((n, d), c) • Sign RSASP 1((n, d), m) • Verify RSAVP 1((n, e), s) Basically exponentiation with differently named inputs!! Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 Encryption scheme • Combines encryption primitive with an encryption encoding method • message encoded message integer message representative encrypted message Decryption scheme • Combines decryption primitive with a decryption decoding method • encrypted message integer message representative encoded message Original version 1. 5 scheme and new version 2. 0 scheme Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1 Encryption scheme • Combines signature primitive with a signature encoding method. • message encoded message integer message representative signature Decryption scheme • Combines verification primitive with a verification decoding method • signature integer message representative encoded • message Original version 1. 5 scheme Signature with appendix Códigos y Criptografía Francisco Rodríguez Henríquez
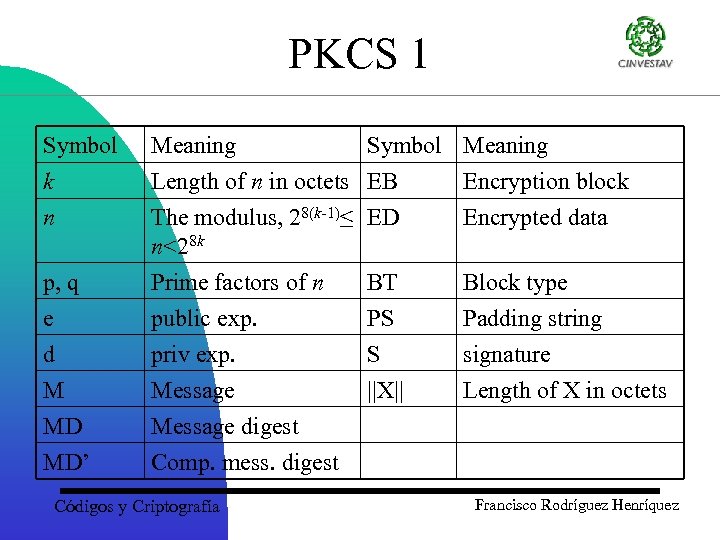
PKCS 1 Symbol k n Meaning Symbol Meaning Length of n in octets EB Encryption block The modulus, 28(k-1)≤ ED Encrypted data n<28 k p, q e d M MD MD’ Prime factors of n public exp. priv exp. Message digest Comp. mess. digest Códigos y Criptografía BT PS S ||X|| Block type Padding string signature Length of X in octets Francisco Rodríguez Henríquez

PKCS Data formatting The data is an octet string D, where ||D|| ≤ k-11. BT is a single octet whose hex representation is either 00 or 01. PS is an octet string with ||PS|| = k -3 -||D||. If BT = 00, then all octets in PS are 00; if BT=01, then all octets in PS are FF. Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS Data formatting The formatted data block (called the encryption block) is: EB = 00||BT||PS||00||D. PKCS-Format for a message m most significant byte 00 02 random padding 00 least significant byte message m at least 8 bytes Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS Data formatting i. The leading 00 block ensures that the octet string EB, when interpreted as an integer, is less than the modulus n. ii. If the block type is BT = 00, then either D must begin with a non-zero octet or its legth must be known, in order to permit unambiguous parsing of EB. Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS Data formatting iii. If BT = 01, then unambiguous parsing is always possible. iv. For the reason given in (iii), and to thwart certain potential attacks on the signature mechanism, BT = 01 is recommended. Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS Data formatting Example: Suppose that n is a 1024 -bit modulus (so k = 128). If ||D|| = 20 octets, then ||PS|| = 105 octets, so that ||EB|| = 128 octets. Códigos y Criptografía Francisco Rodríguez Henríquez

Signature process for PKCS #1 1. Message Hashing. Hash the message M using the selected message-digest algorithm to get the octet string MD. 2. Message Digest Encoding. MD and the hash algorithm identifier are combined into an ASN. 1 (Abstract Syntax Notation) value and then BER-encoded (Basic Encoded Rules) to give an octec data string D. Códigos y Criptografía Francisco Rodríguez Henríquez

Signature process for PKCS #1 3. Data block formatting. With data string input D, use the data formatting discussed previously to form octet string EB. 4. Octet-string 2 integer conversion. Let the octets ob EB be EB 1|| EB 2||… ||EBk. Define EB’i to be the integer whose binary representation is the octet EBi (LSB bit is on the right). Códigos y Criptografía Francisco Rodríguez Henríquez

Signature process for PKCS #1 5. RSA Computation. Compute s = md mod n. 6. Integer 2 octet-string conversion. Convert s to an octet string. The signature is S = ED. Códigos y Criptografía Francisco Rodríguez Henríquez

Signature process for PKCS #1 MESSAGE 1. Message Hashing 2. Message Digest Encoding 3. Data block formatting 4. Octet. String 2 integer conversion 5. RSA COmputation 6. Integer 2 octet. String conversion SIGNATURE Códigos y Criptografía Francisco Rodríguez Henríquez

Verification process for PKCS #1 1. Octet-string 2 integer conversion. Reject S if the bit-length of S is not a multiple of 8. Convert S to an integer s as in step 4 of the signature process. Reject the signature is s > n. 2. RSA Computation. Compute m = se mod n. Códigos y Criptografía Francisco Rodríguez Henríquez

Verification process for PKCS #1 3. Integer 2 octet-string conversion. Convert m to an octet string as in step 6 of the signature process. 4. Parsing. Parse EB into a block type BT, a padding string PS, and the data D. 1. Reject if EB cannot be parsed unambiguously. 2. Reject if BT is not one of 00 or 01. 3. Reject if PS consists of < 8 octets or is inconsistent with BT. Códigos y Criptografía Francisco Rodríguez Henríquez

Verification process for PKCS #1 5. Data Decoding. 1. BER-decode D to get a message digest MD and a hash algorithm identifier. 2. Reject if the hashing algorithm does not identify one of MD 2 or MD 5. 6. Message Digest and Comparison. Hash the message M using the selected message-digest algorithm to get the octet string MD’ and compare it with MD obtained in (5). Códigos y Criptografía Francisco Rodríguez Henríquez
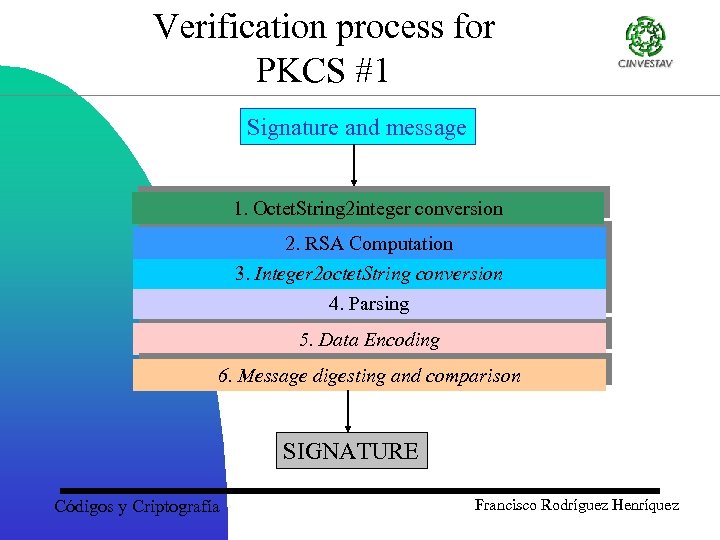
Verification process for PKCS #1 Signature and message 1. Octet. String 2 integer conversion 2. RSA Computation 3. Integer 2 octet. String conversion 4. Parsing 5. Data Encoding 6. Message digesting and comparison SIGNATURE Códigos y Criptografía Francisco Rodríguez Henríquez

PKCS 1: The Future Probabilistic signature scheme (PSS) Provably secure in random oracle model Natural extension to message recovery Códigos y Criptografía Francisco Rodríguez Henríquez
ef98e5a45a2f76278feea742e6d3f480.ppt