Пирамида.ppt
- Количество слайдов: 15
 Пирамида
Пирамида
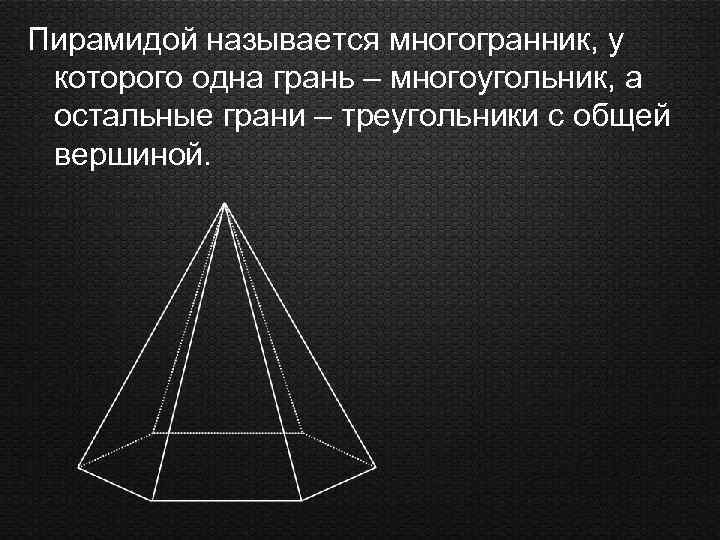 Пирамидой называется многогранник, у которого одна грань – многоугольник, а остальные грани – треугольники с общей вершиной.
Пирамидой называется многогранник, у которого одна грань – многоугольник, а остальные грани – треугольники с общей вершиной.
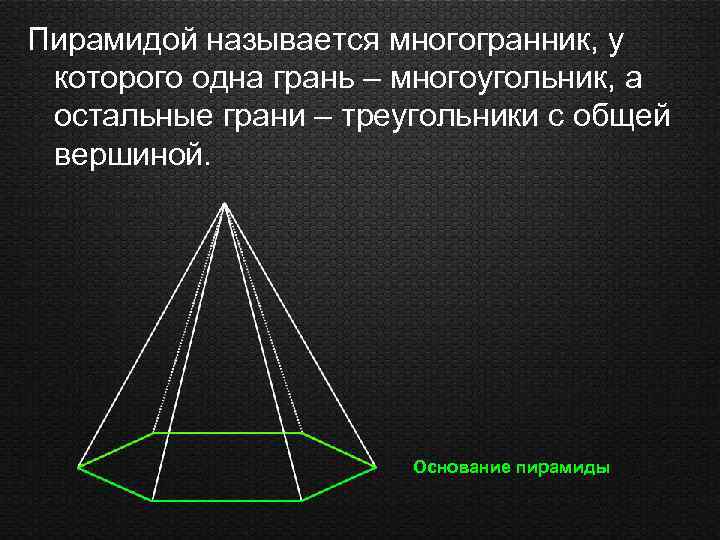 Пирамидой называется многогранник, у которого одна грань – многоугольник, а остальные грани – треугольники с общей вершиной. Основание пирамиды
Пирамидой называется многогранник, у которого одна грань – многоугольник, а остальные грани – треугольники с общей вершиной. Основание пирамиды
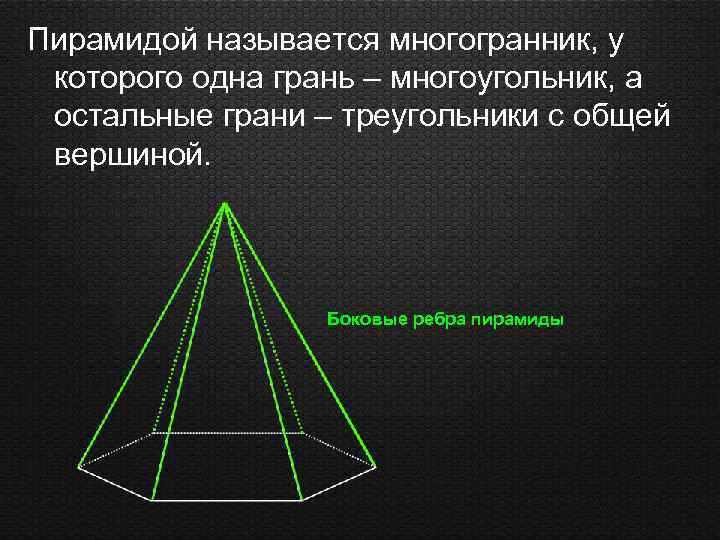 Пирамидой называется многогранник, у которого одна грань – многоугольник, а остальные грани – треугольники с общей вершиной. Боковые ребра пирамиды
Пирамидой называется многогранник, у которого одна грань – многоугольник, а остальные грани – треугольники с общей вершиной. Боковые ребра пирамиды
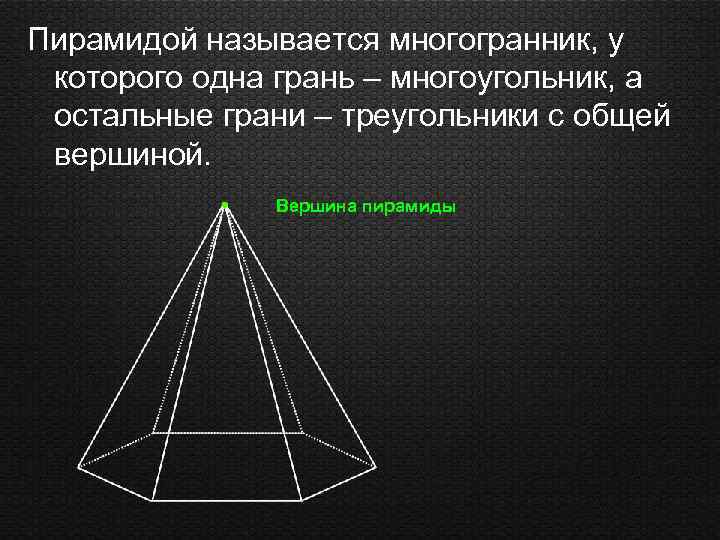 Пирамидой называется многогранник, у которого одна грань – многоугольник, а остальные грани – треугольники с общей вершиной. Вершина пирамиды
Пирамидой называется многогранник, у которого одна грань – многоугольник, а остальные грани – треугольники с общей вершиной. Вершина пирамиды
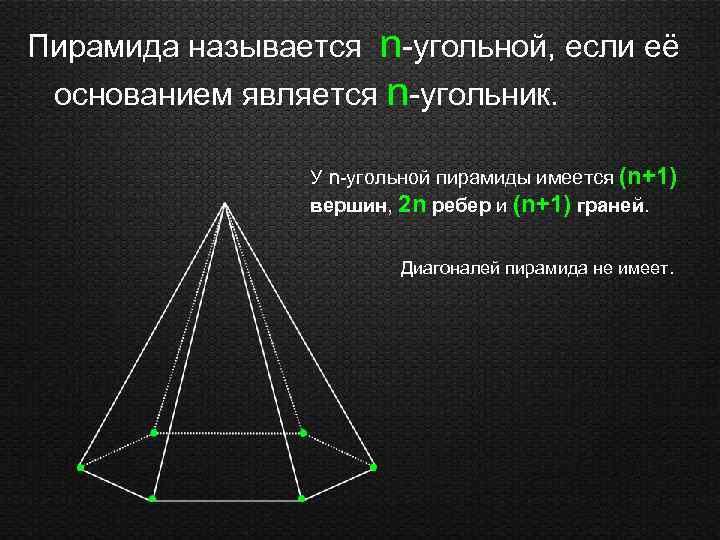 n-угольной, если её основанием является n-угольник. Пирамида называется У n-угольной пирамиды имеется (n+1) вершин, 2 n ребер и (n+1) граней. Диагоналей пирамида не имеет.
n-угольной, если её основанием является n-угольник. Пирамида называется У n-угольной пирамиды имеется (n+1) вершин, 2 n ребер и (n+1) граней. Диагоналей пирамида не имеет.
 Треугольную пирамиду называют также тетраэдром. Тетраэдр – это многогранник с наименьшим числом граней. Любая грань тетраэдра может быть принята за его основание.
Треугольную пирамиду называют также тетраэдром. Тетраэдр – это многогранник с наименьшим числом граней. Любая грань тетраэдра может быть принята за его основание.
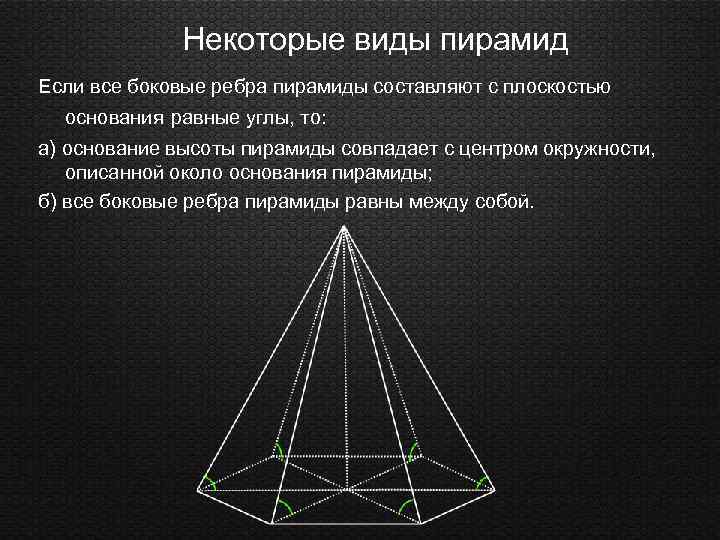 Некоторые виды пирамид Если все боковые ребра пирамиды составляют с плоскостью основания равные углы, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые ребра пирамиды равны между собой.
Некоторые виды пирамид Если все боковые ребра пирамиды составляют с плоскостью основания равные углы, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые ребра пирамиды равны между собой.
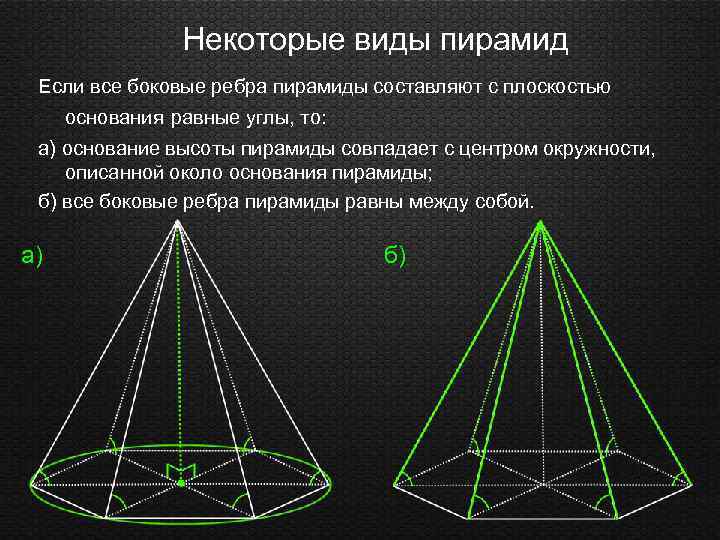 Некоторые виды пирамид Если все боковые ребра пирамиды составляют с плоскостью основания равные углы, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые ребра пирамиды равны между собой. а) б)
Некоторые виды пирамид Если все боковые ребра пирамиды составляют с плоскостью основания равные углы, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые ребра пирамиды равны между собой. а) б)
 Верно и обратное: 1. Если основание высоты пирамиды совпадает с центром окружности, описанной около ее основания, то: а) все боковые ребра пирамиды образуют с плоскостью основания равные углы; б) все боковые ребра пирамиды равны между собой. 2. Если все боковые ребра пирамиды равны, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые ребра пирамиды составляют с плоскостью ее основания равные между собой углы.
Верно и обратное: 1. Если основание высоты пирамиды совпадает с центром окружности, описанной около ее основания, то: а) все боковые ребра пирамиды образуют с плоскостью основания равные углы; б) все боковые ребра пирамиды равны между собой. 2. Если все боковые ребра пирамиды равны, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые ребра пирамиды составляют с плоскостью ее основания равные между собой углы.
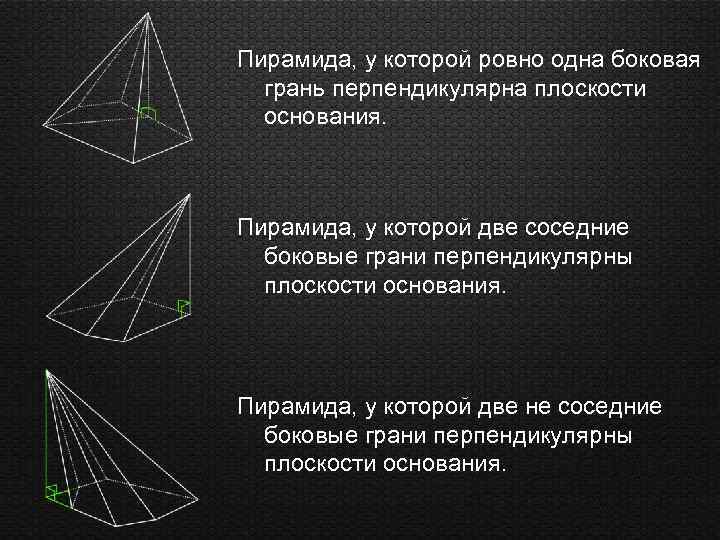 Пирамида, у которой ровно одна боковая грань перпендикулярна плоскости основания. Пирамида, у которой две соседние боковые грани перпендикулярны плоскости основания. Пирамида, у которой две не соседние боковые грани перпендикулярны плоскости основания.
Пирамида, у которой ровно одна боковая грань перпендикулярна плоскости основания. Пирамида, у которой две соседние боковые грани перпендикулярны плоскости основания. Пирамида, у которой две не соседние боковые грани перпендикулярны плоскости основания.
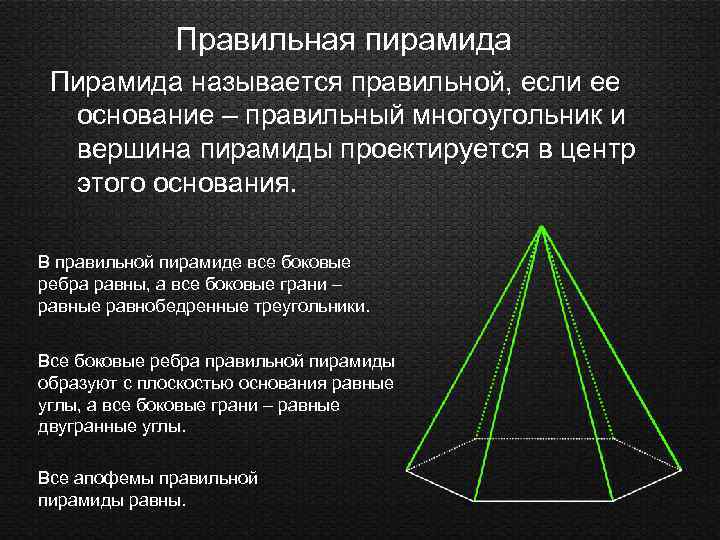 Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник и вершина пирамиды проектируется в центр этого основания. В правильной пирамиде все боковые ребра равны, а все боковые грани – равные равнобедренные треугольники. Все боковые ребра правильной пирамиды образуют с плоскостью основания равные углы, а все боковые грани – равные двугранные углы. Все апофемы правильной пирамиды равны.
Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник и вершина пирамиды проектируется в центр этого основания. В правильной пирамиде все боковые ребра равны, а все боковые грани – равные равнобедренные треугольники. Все боковые ребра правильной пирамиды образуют с плоскостью основания равные углы, а все боковые грани – равные двугранные углы. Все апофемы правильной пирамиды равны.
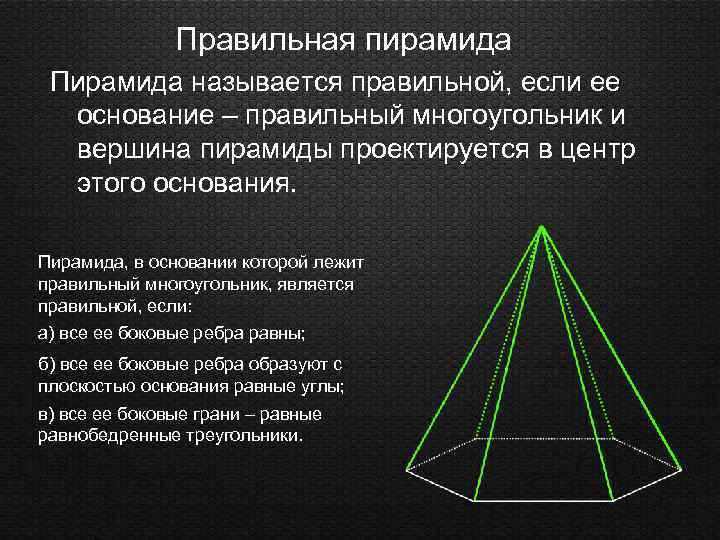 Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник и вершина пирамиды проектируется в центр этого основания. Пирамида, в основании которой лежит правильный многоугольник, является правильной, если: а) все ее боковые ребра равны; б) все ее боковые ребра образуют с плоскостью основания равные углы; в) все ее боковые грани – равные равнобедренные треугольники.
Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник и вершина пирамиды проектируется в центр этого основания. Пирамида, в основании которой лежит правильный многоугольник, является правильной, если: а) все ее боковые ребра равны; б) все ее боковые ребра образуют с плоскостью основания равные углы; в) все ее боковые грани – равные равнобедренные треугольники.
 Теорема 17. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра на апофему пирамиды. Теорема 18. Если все боковые грани пирамиды наклонены к плоскости основания под углом α, и высота пересекает основание, то Sбок= Sосн /cosα Теорема 19. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые ребра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник, подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Теорема 17. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра на апофему пирамиды. Теорема 18. Если все боковые грани пирамиды наклонены к плоскости основания под углом α, и высота пересекает основание, то Sбок= Sосн /cosα Теорема 19. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые ребра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник, подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.



