Пирамида
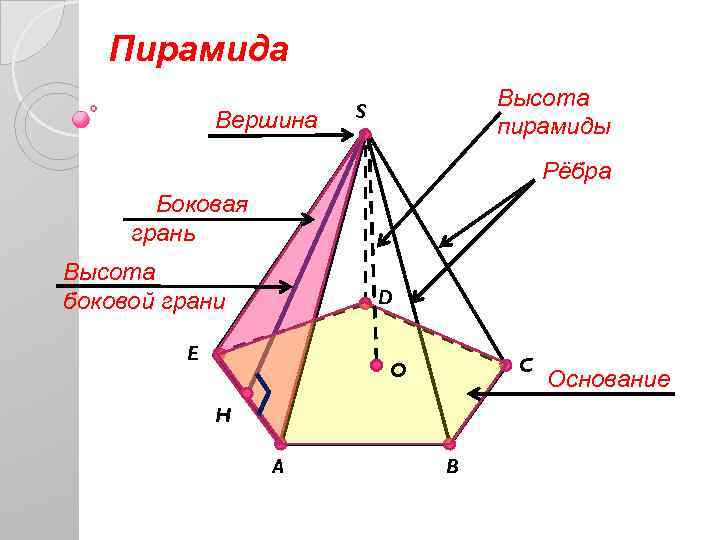
Пирамида Вершина Высота пирамиды S Рёбра Боковая грань Высота боковой грани D E C O H A B Основание
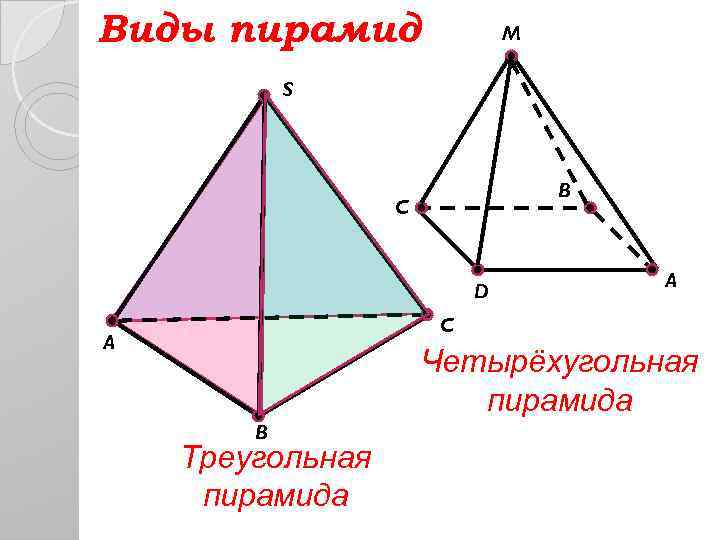
Виды пирамид M S B C D A C A Четырёхугольная пирамида B Треугольная пирамида
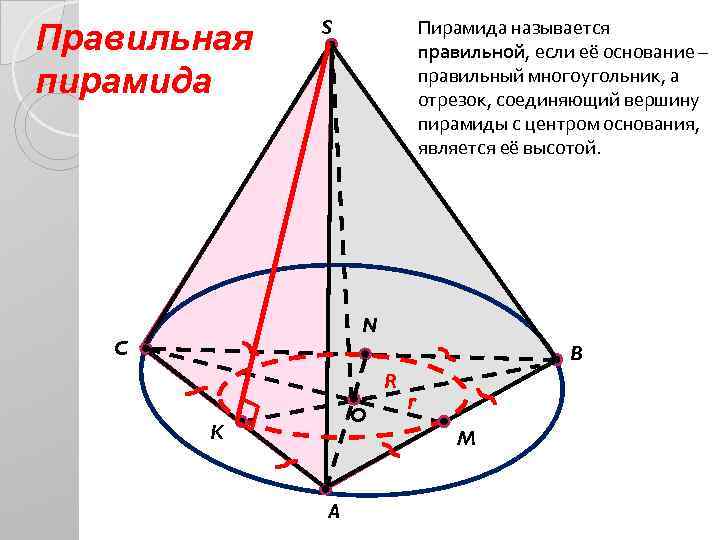
Правильная пирамида Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой. S N C B R O K A r M
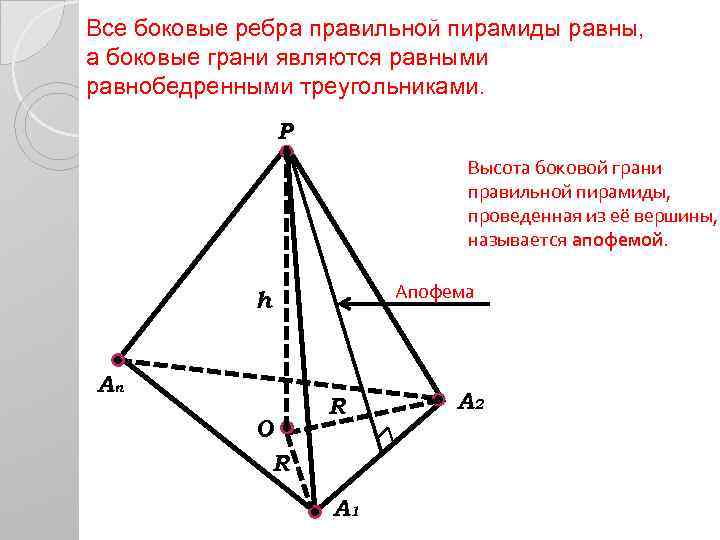
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. P Высота боковой грани правильной пирамиды, проведенная из её вершины, называется апофемой. Апофема h An O R R A 1 A 2
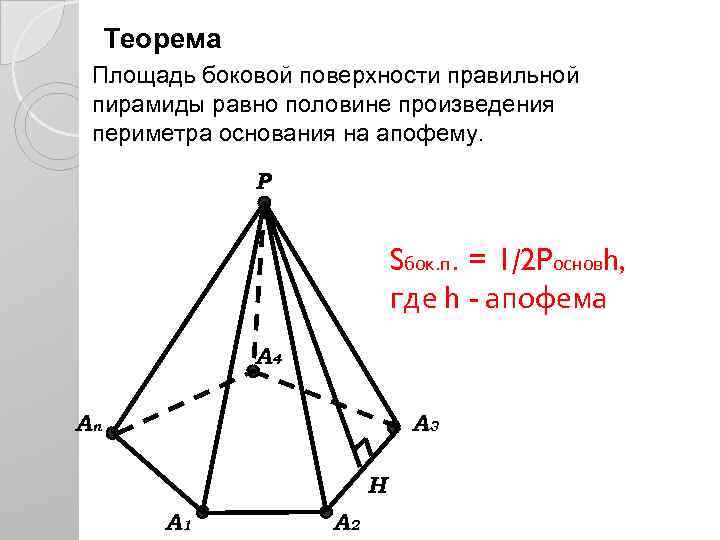
Теорема Площадь боковой поверхности правильной пирамиды равно половине произведения периметра основания на апофему. P Sбок. п. = 1/2 Pосновh, где h - апофема A 4 An A 3 H A 1 A 2
Усечённая пирамида M Теорема C 1 B 1 A 1 D 1 Площадь боковой поверхности правильной усеченной пирамиды равно произведению полусуммы периметров оснований на апофему. h C D B A
Домашняя работа П. 32 -33, № 239, 243, 244
Скачать презентацию Пирамида Пирамида Вершина Высота пирамиды S Рёбра
Пирамида.pptx