Пифагор Самосский родился около 570, умер ок. 500

Пифагор Самосский родился около 570, умер ок. 500 до н. э. Древнегреческий философ и математик, основатель пифагорейской школы. В Школе Пифагора впервые высказана догадка о шарообразности Земли. Письменных документов о Пифагоре не осталось. .

Система обучения в этой школе была сложной, многолетней. Желающие приобщиться к знанию должны пройти испытательный срок от 3 до 5 лет. Все это время ученики обязаны хранить молчание и только слушать. Из его школы вышли выдающиеся политические и государственные деятели, историки, математики и астрономы. Пифагор развил теорию музыки и акустики, создав знаменитую "пифагорейскую гамму" и проведя основополагающие эксперименты по изучению музыкальных тонов. Основной тезис пифагорейцев: "Все веши - суть числа".

Вот некоторые предписания пифагорейского ордена: 1. Воздерживайся от употребления в пищу бобов. 2. Не поднимай то, что упало. 3. Не прикасайся к белому петуху. 4. Не ломай хлеба. 5. Не шагай через перекладину. 6. Не размешивай огонь железом. 7. Не откусывай от целой булки. 8. Не ощипывай венок. 9. Не сиди на мерке в одну кварту. 10. Сердца не ешь. 11. Не ходи по большой дороге. 12. Не дозволяй ласточкам жить под крышей. 13. Вынимай горшок из огня, не оставляй следа его на золе, не помешай золу. 14. Не смотрись в зеркало около огня.

-Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться. - Не делай никогда того, чего ты не знаешь. Но научись всему, что следует знать, и тогда ты будешь вести спокойную жизнь. - Не пренебрегай здоровьем, своего тела. Доставляй ему вовремя пищу и питье, и упражнения, в которых оно нуждается. - Приучайся жить просто и без роскоши. - Не закрывай глаз, когда хочется спать, не разобравши всех своих поступков в прошедший день. - Не проходите мимо весов (то есть не нарушайте справедливости). - Не садитесь на подушку (то есть не успокаивайтесь на достигнутом). - Не грызите своего сердца (то есть не предавайтесь меланхолии). - Не поправляйте огня мечем (то есть не раздражайте тех, кто и без того во гневе). - Не принимайте под свою кровлю ласточек (то есть говорунов и легкомысленных людей).

"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол". Евклид.

"В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол". Ф. И. Петрушевский

"Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол". Герхад Клемонский.

Квадрат гипотенузы равен сумме квадратов катетов. a 2+b 2=c 2

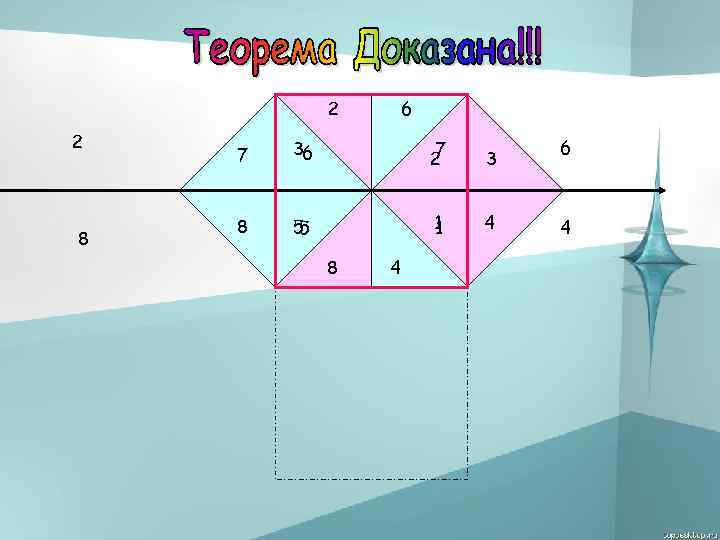2 2 8 6 7 36 7 2 3 8 5 5 1 1 4 8 4 6 4

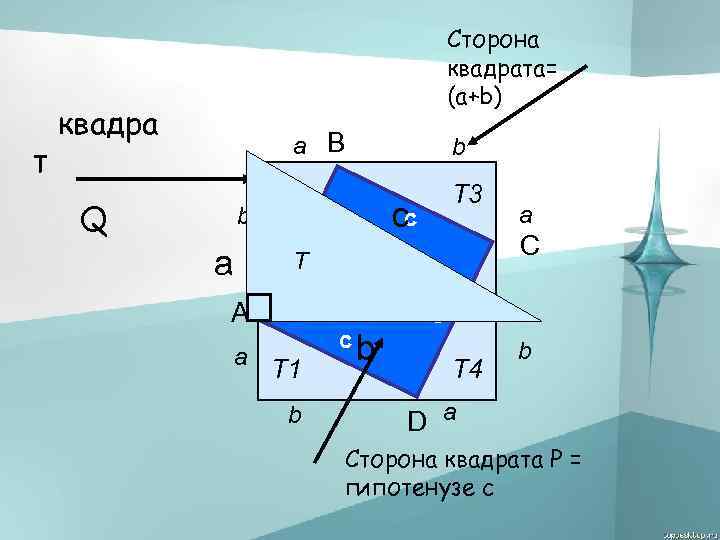т Сторона квадрата= (а+b) квадра a B Q b a T 2 T A a b cc c b b a C P c T 1 T 3 c T 4 b D a Сторона квадрата Р = гипотенузе с

f 7 e 5 3 (4) 1 (2) 3 1 8 5 4 a l 6 2 4 2 Угол 1 = 5 Угол 90º - угол 1 = угол 3 8 90º 6 ∆Угол 2 т. кгипотенузе и 3 4∆ װ по угол=> = װ угол = 6 - װ углу ∆2 по гипотенузе и они=>соотв. װ װ װ ∆ 1 = острому углу секущей Угол и 90º уголуглуугол 4 7 90º - - угол 5 угол Уголострому 2 = = а c k при l װ k

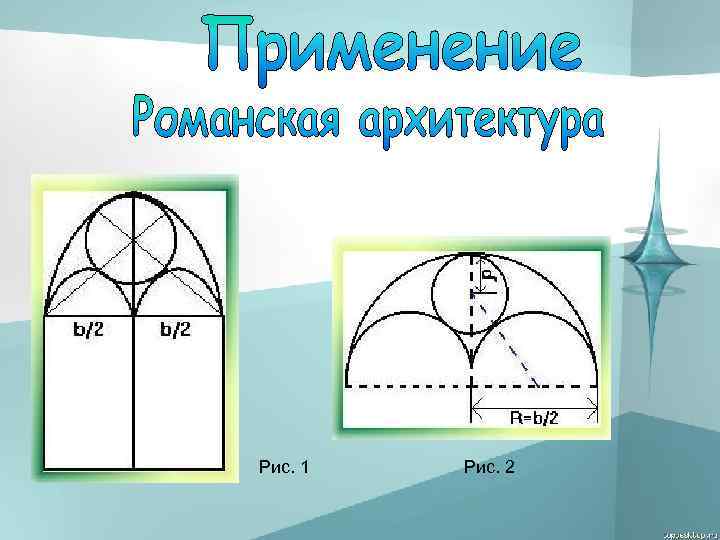Рис. 1 Рис. 2

Хронология развития теоремы Пифагора № Историческое место дата 1 Древний Китай (математическая книга Чу-пей) ~2400 г. до н. э. 2 Древний Египет (гарпедонапты или "натягиватели веревок") 2300 г. до н. э. 3 Вавилон (Хаммураби ) 2000 г. до н. э. 4 Древняя Индия (сборник Сульвасутра ) 5 Пифагор 600 г. до н. э. 570 г. до н. э.

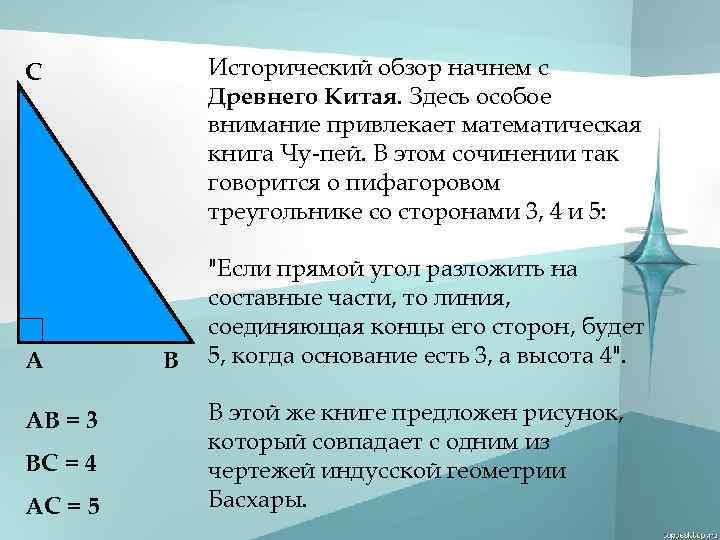Исторический обзор начнем с Древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: С А АВ = 3 ВС = 4 АС = 5 В "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4". В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э. , во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Георг Кантор

Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3 м. от одного конца и 4 метра от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.

Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э. , приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Хаммураби

В самом древнем индийском геометрическом сборнике «Сульвасутра» ( «Правила веревки» , 600 год до н. э. ), представляющем собой своеобразную инструкцию по сооружению алтарей в храмах, даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины).

Как утверждают все античные авторы, Пифагор первый дал полноценное доказательство теоремы, носящей его имя. К сожалению, мы не знаем, в чем оно состояло, потому что древние математики и писатели об этом умалчивают, а от самого Пифагора и ранних пифагорейцев до нас не дошло ни одного письменного документа. Только позже у Евклида было обнаружено доказательство этой теоремы. Пифагор

На рисунке три прямоугольных треугольника составляют трапецию. Поэтому площадь этой фигуры можно находить по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников. В первом случае эта площадь равна 0. 5(a+b)2, во втором – 0. 5 ab+0. 5 c 2. Приравнивая эти выражения, получаем теорему Пифагора. Теорема доказана.

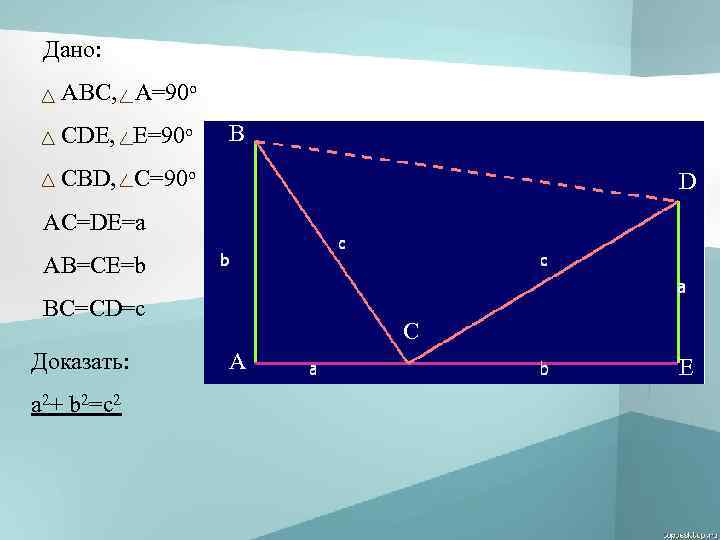Дано: АВС, A=90 o СDE, E=90 o B CBD, C=90 o D AC=DE=a AB=CE=b BC=CD=c Доказать: a 2+ b 2=c 2 C A E

Доказательство Рассмотрим трапецию ABDE: S = (a+b) ABDE С другой стороны: S = ABDE Получим: Теорема доказана