87_.ppt.pptx
- Количество слайдов: 7
 Пифагор (Самосский) и его жизнь
Пифагор (Самосский) и его жизнь
 Пифагор- математик, древне греческий философ, основатель пифагореизма, религиозный и политический деятель. Родился около 570 г. до н. э. На самосском острове. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора были старец Гермодамант и Ферекид Сиросский. Известно, что Пифагор посетил множество стран и учился у многих мыслителей того времени.
Пифагор- математик, древне греческий философ, основатель пифагореизма, религиозный и политический деятель. Родился около 570 г. до н. э. На самосском острове. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора были старец Гермодамант и Ферекид Сиросский. Известно, что Пифагор посетил множество стран и учился у многих мыслителей того времени.
 У Пифагора также была страсть к музыке. Он целые дни проводил у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Главный вклад Пифагора в развитие музыки заключался в учении о пропорциях звуков. За основу были взяты струнные инструменты, представлявшие собой доску с натянутыми струнами. В результате многочисленных опытов были найдены определенные числовые выражения(интервальные коэффициенты). Отсчитывая последовательно квинты от исходного звука и перенося их в одну октаву, можно было получить числовое значение любого звука диатонической или хроматической гаммы.
У Пифагора также была страсть к музыке. Он целые дни проводил у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Главный вклад Пифагора в развитие музыки заключался в учении о пропорциях звуков. За основу были взяты струнные инструменты, представлявшие собой доску с натянутыми струнами. В результате многочисленных опытов были найдены определенные числовые выражения(интервальные коэффициенты). Отсчитывая последовательно квинты от исходного звука и перенося их в одну октаву, можно было получить числовое значение любого звука диатонической или хроматической гаммы.
 Школа Пифагора В кротоне Пифагор открывает свою школу, которая действовала около тридцати лет. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно философской школой, политической партией, и религиозным братством. Статут пифагорейского союза был очень суровым. Каждый, кто вступал в него, отказывался от личной собственности в пользу союза, обязывался не проливать крови, не употреблять мясной пищи, беречь тайну учения своего учителя. Членам школы запрещалось обучать других за вознаграждение. По своим философским взглядам Пифагор был идеалистом, защитником интересов
Школа Пифагора В кротоне Пифагор открывает свою школу, которая действовала около тридцати лет. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно философской школой, политической партией, и религиозным братством. Статут пифагорейского союза был очень суровым. Каждый, кто вступал в него, отказывался от личной собственности в пользу союза, обязывался не проливать крови, не употреблять мясной пищи, беречь тайну учения своего учителя. Членам школы запрещалось обучать других за вознаграждение. По своим философским взглядам Пифагор был идеалистом, защитником интересов
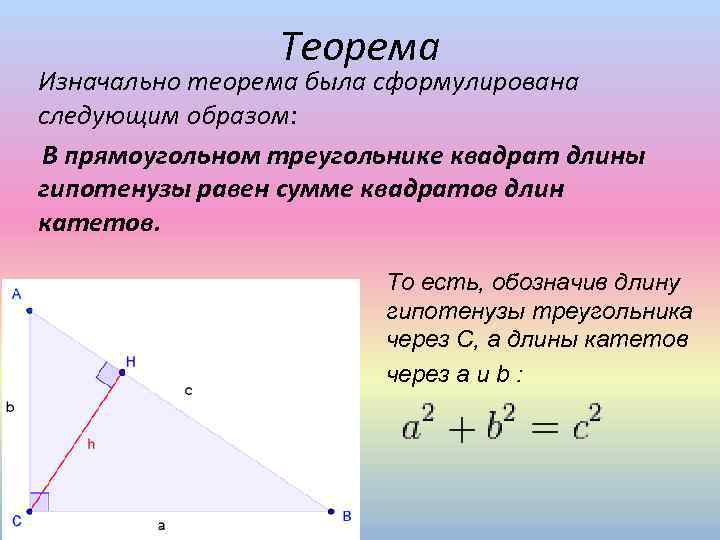 Теорема Изначально теорема была сформулирована следующим образом: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, обозначив длину гипотенузы треугольника через С, а длины катетов через а и b :
Теорема Изначально теорема была сформулирована следующим образом: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, обозначив длину гипотенузы треугольника через С, а длины катетов через а и b :
 На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства. Способы: • Простейшее доказательство. • Доказательство Евклида • Алгебраическое доказательство • Доказательство через косинус угла • Векторное док-во • Доказательство методом Гарфилда
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства. Способы: • Простейшее доказательство. • Доказательство Евклида • Алгебраическое доказательство • Доказательство через косинус угла • Векторное док-во • Доказательство методом Гарфилда
 Заключение В наши дни теорема Пифагора очень важна и актуальна. И несущественно то, что она была известна за много веков до Пифагора, важно то, что Пифагор выделил её, дополнив собственными исследованиями, повысив значимость в мире математических открытий. Из неё или с её помощью можно вывести большинство теорем геометрии. Теорема Пифагора продолжает оставаться живительным источником красоты, совершенства и творчества для новых и новых поколений. Несмотря на то что, суть теоремы проста и изящна, но было бы ошибкой думать, что в плане её содержания не осталось места для каких-то новых исследований. Результатом одного из таких исследований являются Пифагоровы тройки - наборы из трёх натуральных чисел, из которых сумма квадратов двух чисел равна квадрату третьего числа…
Заключение В наши дни теорема Пифагора очень важна и актуальна. И несущественно то, что она была известна за много веков до Пифагора, важно то, что Пифагор выделил её, дополнив собственными исследованиями, повысив значимость в мире математических открытий. Из неё или с её помощью можно вывести большинство теорем геометрии. Теорема Пифагора продолжает оставаться живительным источником красоты, совершенства и творчества для новых и новых поколений. Несмотря на то что, суть теоремы проста и изящна, но было бы ошибкой думать, что в плане её содержания не осталось места для каких-то новых исследований. Результатом одного из таких исследований являются Пифагоровы тройки - наборы из трёх натуральных чисел, из которых сумма квадратов двух чисел равна квадрату третьего числа…


