Скачать презентацию PIEŢE DE CAPITAL Elementele structurale cursului
0ead820ce90da04778393c28aee02f2c.ppt
- Количество слайдов: 105
PIEŢE DE CAPITAL
Elementele structurale cursului • Cursul de Piete de Capital se adreseaza studentilor inscrisi la programul de studiu ID, organizat de facultatea Finante, Asigurari, Banci si Burse de Valori si face parte din planul de invatamant aferent anului II, semestrul 2 • Obiectivele acestui curs sunt: ü cunoaşterea modului de organizare şi funcţionare a pieţei de capital; ü identificarea relaţiilor dintre instituţiile pieţei de capital; ü cunoaşterea principiilor de funcţionare a organismelor de plasament colectiv şi a randamentului investiţiilor administrate; ü însuşirea caracteristicilor instrumentelor financiare şi a modalităţilor de evaluare a acestora; ü însuşirea cadrului reglementar funcţional pe piaţa de capital din România şi pe cea europeană. ü Evaluarea cunostintelor se va realiza prin examenul sustinut in perioada de sesiune
Cuprinsul Cursului 1. 2. 3. 4. 5. Caracterizarea pieţei de capital………………. pag 5 Instrumente financiare……………. pag 14 Tranzacţii bursiere………………pag Instrumente financiare derivate ………………. pag Indici bursieri…………………. . pag
Bibliografie • • • Anghelache G. , “Piaţa de capital: caracteristici, evoluţii, tranzacţii”, Ed. Economică, Bucureşti, 2004 Anghelache G. şi colectiv, “Pieţe de capital şi tranzacţii bursiere” – aplicaţii şi studii de caz, Ed. Economică, Bucureşti, 2003 Bodie, Z. , A. Kane, and A. J. Marcus (2007), Essentials of Investments, 6 th edition, Mc. Graw Hill International Edition
I. Caracterizarea pieţei de capital • Obiectivele unității de învățare I: - familiarizarea cu piața de capital prin prisma componentelor sale principale (piață primară și piață secundară) - înțelegerea modului în care diverși participanți își derulează activitatea pe piața de capital - înțelegerea fenomenelor de cerere și ofertă de capital
I. Caracterizarea pieţei de capital • Cuprinsul unităţii de învăţare 1: - Definirea pietei de capital …………………. . pag 7 Participantii la piata de capital…………. . . …pag 8 Cererea si oferta de capital…………. . …. …. pag 9 Structura pietei de capital……………. . …. …pag 10 Teste de autoevaluare…………. …pag 11 Raspunsuri la testele de autoevaluare…. …. pag 12 Bibliografie…………………. pag 13
I. Caracterizarea pieţei de capital • Piaţa de capital • Conceptul anglo-saxon • Conceptul continental-european • România: accepţiunea anglo-saxonă: piaţa de capital este o componentă a pieţei financiare, interconectează emitenţii şi investitorii • Piaţa financiară: alternativă la finanţarea intermediată; asigură finanţarea directă
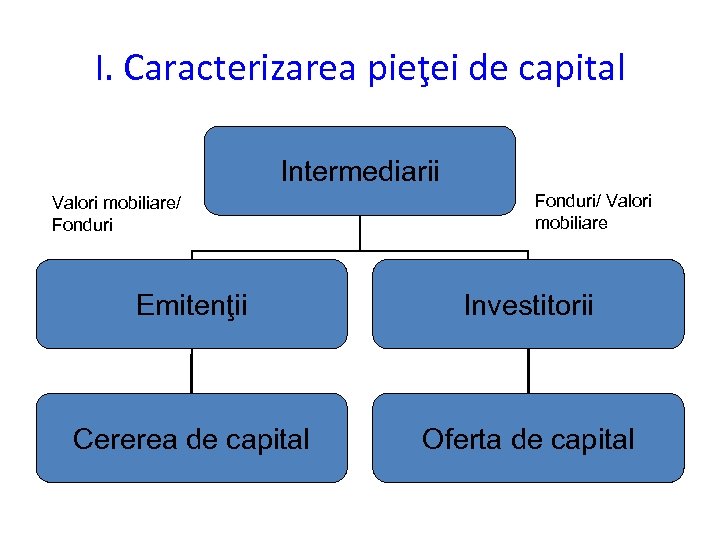I. Caracterizarea pieţei de capital Intermediarii Valori mobiliare/ Fonduri/ Valori mobiliare Emitenţii Investitorii Cererea de capital Oferta de capital
I. Caracterizarea pieţei de capital • Cererea de capital Debitorii: d. p. d. v. al activităţii desfăşurate d. p. d. v. al scopului urmărit Cererea de capital: - Structurală - Conjuncturală • Oferta de capital Investitorii: - Individuali: - pasivi - activi - Instituţionali
I. Caracterizarea pieţei de capital • • - Structura pieţei de capital d. p. d. v. al producerii şi comercializării valorilor mobiliare piaţa primară piaţa secundară • - d. p. d. v. al obiectului tranzacţiei piaţa acţiunilor piaţa obligaţiunilor piaţa contractelor la termen piaţa opţiunilor • - d. p. d. v. al modului de formare al preţurilor piaţa de licitaţie piaţa de negocieri • - d. p. d. v. al momentului finalizării tranzacţiilor piaţa la vedere piaţa la termen
I. Caracterizarea pieţei de capital • 1. 2. 3. 4. Teste de autoevaluare Trăsăturile pieței de capital vizează: a) investirea capitalurilor disponibile în titluri emise pe termen mediu și lung; b) transferul liber al instrumentelor pieței de capital între posesori; c) caracterul public al tranzacțiilor cu titluri; d) stabilirea prețurilor titlurilor pe piața bursieră prin negociere și pe piața extrabursieră prin licitație; e) asigurarea legăturii între solicitatorii de titluri și ofertanții acestora cu ajutorul intermediarilor specializați. Care din trăsăturile enumerate mai sus nu este adevarată? Conform accepțiunii europene asupra piețelor de capital: a) structura pieței de capital include piața financiară, piața monetară, piața ipotecară; b) resursele mobilizate pe piața ipotecară sunt capitaluri disponibile pe termen scurt; c) participanții pe piața monetară sunt băncile centrale și comerciale, casele de economii, societățile de asigurări, trezoreria publică; d) obiectul operațiunilor pe piața financiară este emisiunea, plasarea și tranzacționarea titlurilor de capital pe termen lung; e) pe piața monetară se tranzacționează monede, efecte de comerț, certificate de depozit, bonuri de tezaur. Care din afirmațiile de mai sus nu este adevarată? Investitorii instituționali pe piața de capital: a) realizează tranzacții de dimensiuni modeste; b) cumpără și păstrează valorile mobiliare urmărind creșterea ratei dobânzii de piață; c) au un impact redus asupra variației prețului zilnic al valorilor mobiliare; d) sunt reprezentați de persoane fizice care încearcă valorificarea mișcării cursului bursier pentru obținerea de profit; e) exercită o influență semnificativă asupra volumului tranzacțiilor. Alegeți afirmația corectă. Funcționarea eficientă a pieței secundare de capital este legată de abundența de fonduri și titluri pe piață. Această cerință este reprezentată de: a) adaptabilitate; b) corectitudine; c) lichiditate; d) transparență; e) eficiența pieței de capital.
I. Caracterizarea pieţei de capital • Raspunsuri la testele de autoevaluare 1–D 2–B 3–E 4–C
I. Caracterizarea pieţei de capital • Anghelache G. , “Piaţa de capital: caracteristici, evoluţii, tranzacţii”, Ed. Economică, Bucureşti, 2004 • Anghelache G. şi colectiv, “Pieţe de capital şi tranzacţii bursiere” – aplicaţii şi studii de caz, Ed. Economică, Bucureşti, 2003
II. Instrumente financiare • Cuprinsul unităţii de învăţare 2: - Definirea instrumentelor financiare ………. . pag 16 Acţiuni……………. . . …pag 20 Acţiuni – Aplicaţii rezolvate. …………. . …. …. pag 33 Acţiuni – Aplicaţii propuse……………. . …. …pag 37 Obligaţiuni……………. …pag 39 Teste de autoevaluare…………. …pag 42 Raspunsuri la testele de autoevaluare…. …. pag 43 Paralela acţiuni-obligaţiuni. . . . pag 44 Obligaţiuni – Aplicaţii rezolvate…………. …. pag 45 Obligaţiuni – Aplicaţii propuse…………. . . …. pag 51 Bibliografie…………………. pag 53
II. Instrumente financiare • Obiectivele unității de învățare II: - definirea instrumentelor financiare primare (acțiuni și obligațiuni) - analiza majorărilor de capital prin emisiune de noi acțiuni în schimbul numerarului sau prin încorporarea unei părți din rezerve - evaluarea fundamentală și tehnică a acțiunilor – elemente în decizia de investire pe piața de capital - caracterizarea împrumuturilor obligatare – ca modalitate de finanțare directă a activității unui agent economic - evaluarea împrumuturilor obligatare
II. Instrumente financiare • Conform Directivelor UE: - Valori mobiliare - Titluri de participare ale organismelor de plasament colectiv - Instrumente ale pieţei monetare - Contracte futures, forward, swap, opţiuni - Instrumente financiare derivate pe mărfuri - Orice alt instrument admis la tranzacţionare pe o piaţă reglementată dintr-un stat membru al UE
II. Instrumente financiare • Valorile mobiliare includ: - Acţiuni emise de societăţi comerciale negociabile pe piaţa de capital - Obligaţiunile şi titlurile de creanţă negociabile pe piaţa de capital - Orice alte titluri negociabile care dau dreptul de a achiziţiona valori mobiliare prin subscriere sau schimb, generând o decontare în bani, cu excepţia instrumentelor de plată Valorile mobiliare sunt o formă de existenţă a activelor nebancare
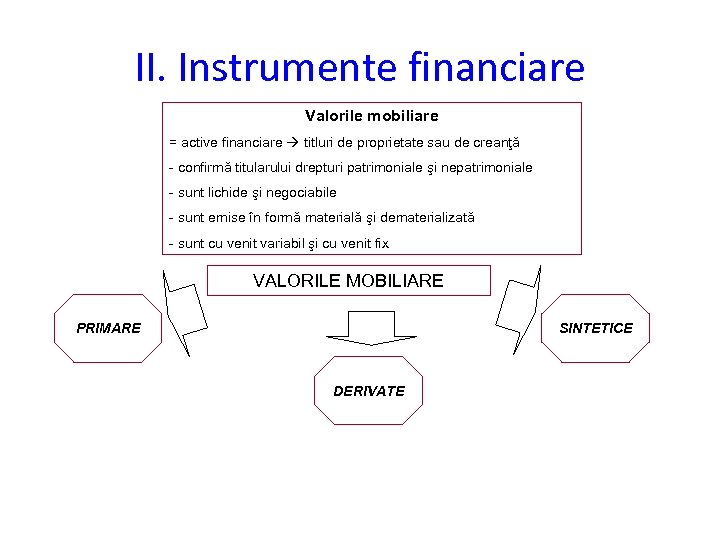II. Instrumente financiare Valorile mobiliare = active financiare titluri de proprietate sau de creanţă - confirmă titularului drepturi patrimoniale şi nepatrimoniale - sunt lichide şi negociabile - sunt emise în formă materială şi dematerializată - sunt cu venit variabil şi cu venit fix VALORILE MOBILIARE PRIMARE SINTETICE DERIVATE
II. Instrumente financiare • - Valorile mobiliare sunt caracterizate prin: Sunt instrumente negociabile Pot fi emise în formă materializată sau dematerializată Generează drepturi patrimoniale şi nepatrimoniale • Instrumente financiare derivate: - Contracte la termen - Opţiuni • Instrumente financiare sintetice
II. 1. Acţiuni • - Caracteristicile acţiunilor: Sunt fracţiuni ale capitalului social Sunt fracţiuni egale capitalului social Sunt indivizibile Sunt instrumente negociabile • • Clasificarea acţiunilor: D. p. d. v. al modului de identificare a deţinătorului: - • - Nominative La purtator D. p. d. v. al drepturilor pe care le generează: Acţiuni ordinare Acţiuni preferenţiale D. p. d. v. al emitentului: Acţiuni autorizate Acţiuni neemise Acţiuni puse în vânzare Acţiuni aflate pe piaţă Acţiuni de trezorerie
II. 1. Acţiuni • - Emisiunea de noi acţiuni: La înfiinţarea agentului economic Pe parcursul existenţei • Dreptul de preferinţă:
II. 1. Acţiuni • Dreptul la dividend • - Politica de dividend: Politica reziduală Politica ratelor Politica stabilizată • - Forme: Dividend anual Dividend fix Dividend provizoriu Dividend sub formă de noi acţiuni
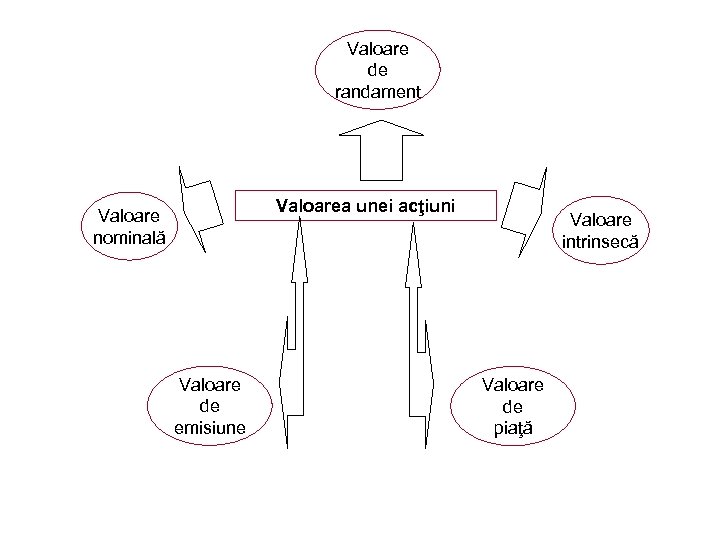Valoare de randament Valoarea unei acţiuni Valoare nominală Valoare de emisiune Valoare intrinsecă Valoare de piaţă
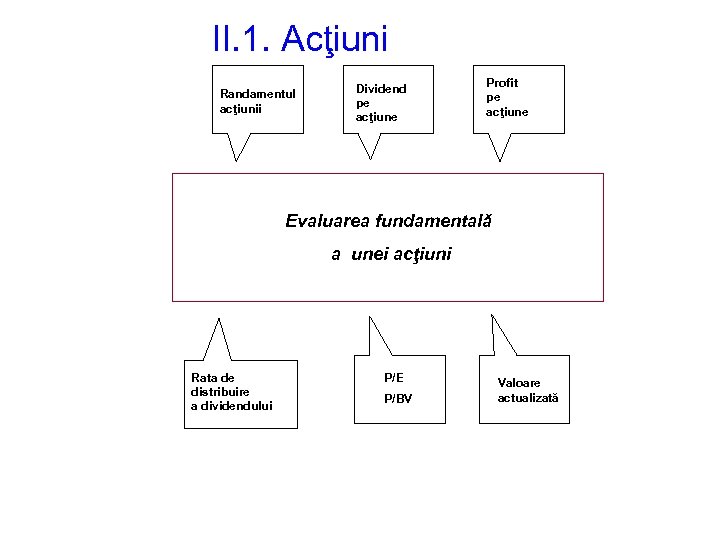II. 1. Acţiuni Randamentul acţiunii Dividend pe acţiune Profit pe acţiune Evaluarea fundamentală a unei acţiuni Rata de distribuire a dividendului P/E P/BV Valoare actualizată
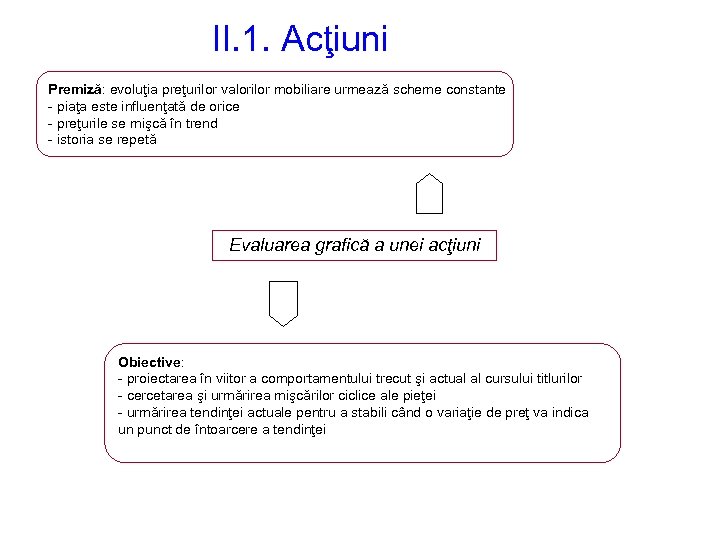II. 1. Acţiuni Premiză: evoluţia preţurilor valorilor mobiliare urmează scheme constante - piaţa este influenţată de orice - preţurile se mişcă în trend - istoria se repetă Evaluarea grafică a unei acţiuni Obiective: - proiectarea în viitor a comportamentului trecut şi actual al cursului titlurilor - cercetarea şi urmărirea mişcărilor ciclice ale pieţei - urmărirea tendinţei actuale pentru a stabili când o variaţie de preţ va indica un punct de întoarcere a tendinţei
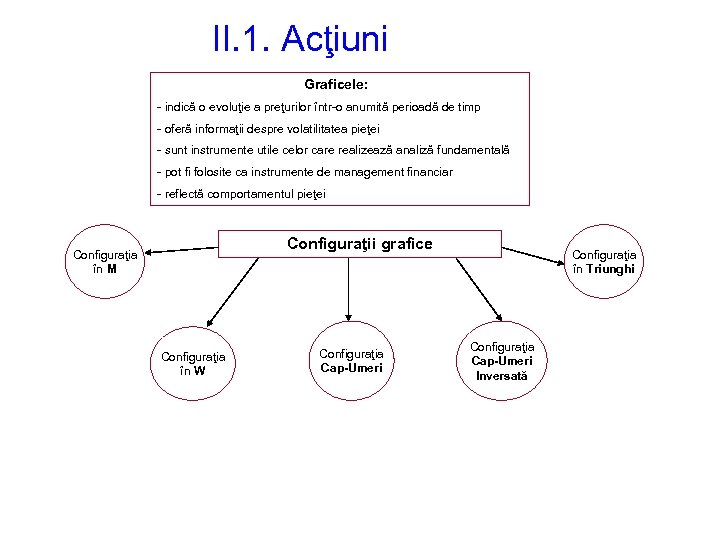II. 1. Acţiuni Graficele: - indică o evoluţie a preţurilor într-o anumită perioadă de timp - oferă informaţii despre volatilitatea pieţei - sunt instrumente utile celor care realizează analiză fundamentală - pot fi folosite ca instrumente de management financiar - reflectă comportamentul pieţei Configuraţii grafice Configuraţia în M Configuraţia în W Configuraţia Cap-Umeri Configuraţia în Triunghi Configuraţia Cap-Umeri Inversată
CONFIGURAŢIA CAP – UMERI (head and shoulders) - perioadă de formare: 2 – 3 luni - componente: umăr stâng, cap, umăr drept, depăşirea liniei gâtului - depăşirea liniei gâtului > trend descrescător > semnal de vânzare - volum maxim tranzacţii: formarea capului graficului
CONFIGURAŢIA CAP – UMERI (head and shoulders) - perioadă de formare: 2 – 3 luni - componente: umăr stâng, cap, umăr drept, depăşirea liniei gâtului - depăşirea liniei gâtului > trend descrescător > semnal de vânzare - volum maxim tranzacţii: formarea capului graficului
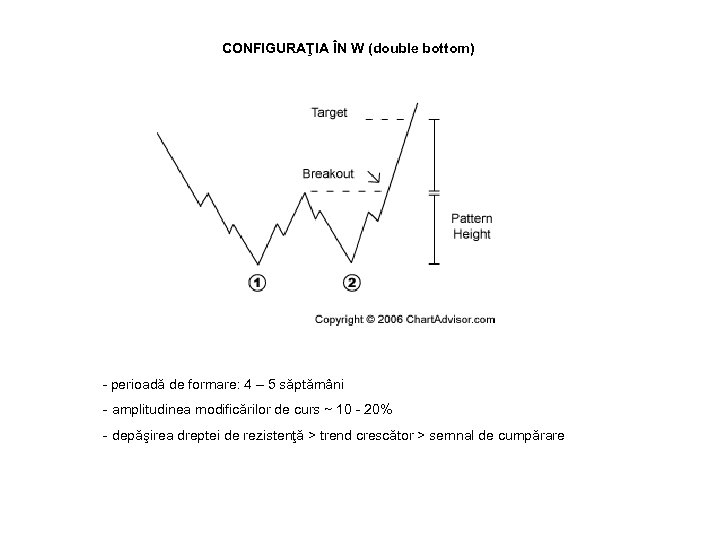CONFIGURAŢIA ÎN W (double bottom) - perioadă de formare: 4 – 5 săptămâni - amplitudinea modificărilor de curs ~ 10 - 20% - depăşirea dreptei de rezistenţă > trend crescător > semnal de cumpărare
CONFIGURAŢIA ÎN M (double top) - semnale: scăderea cursului cu 10 – 20% după primul vârf (1) şi formarea a două vârfuri similare (sau cu diferenţe de 3 – 4%) - depăşirea dreptei suport > trend descrescător > semnal de vânzare
CONFIGURAŢIA ÎN TRIUNGHI SIMETRIC (symmetrical triangle) - perioada de analiză: minim 6 luni - semnale: mişcări succesive de creştere / scădere de curs cu amplitudine din ce în ce mai scăzută şi convergenţă către un singur punct - ieşirea cursului din vârful triunghiului indică trendul viitor de creştere / scădere de curs > semnal de cumpărare / de vânzare
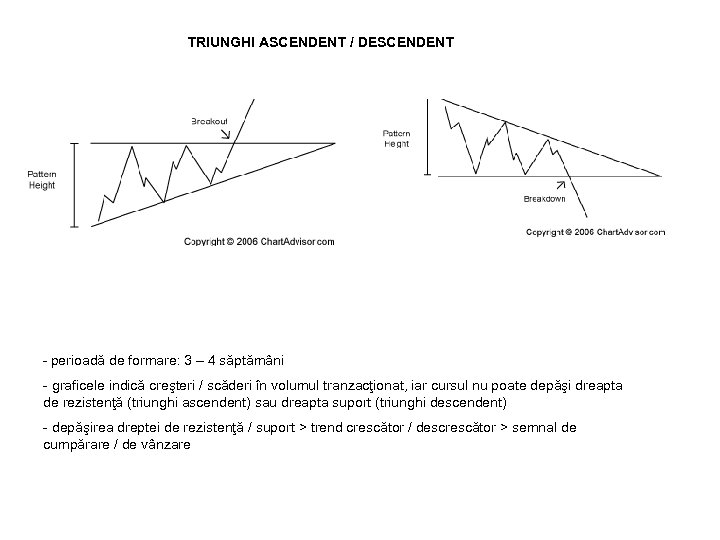TRIUNGHI ASCENDENT / DESCENDENT - perioadă de formare: 3 – 4 săptămâni - graficele indică creşteri / scăderi în volumul tranzacţionat, iar cursul nu poate depăşi dreapta de rezistenţă (triunghi ascendent) sau dreapta suport (triunghi descendent) - depăşirea dreptei de rezistenţă / suport > trend crescător / descrescător > semnal de cumpărare / de vânzare
II. 1. Acţiuni-aplicaţii rezolvate Exemplul 1. Pentru firmele A, B şi C se cunosc următoarele date: ultimul dividend acordat (D 0), rata de creştere a dividendului (g), cursul bursier (P). De asemenea, pe baza datelor istorice s-au estimat parametrii α şi β ai ecuaţiei de regresie: . Toate aceste date sunt grupate în tabelul de mai jos: A B C D 0 (u. m. ) 7 9 14 g (%) 8 5 2 P (u. m. ) 30 60 110 α 0, 01 0, 03 0, 02 Dacă se anticipează un randament al pieţei de 20%, determinati care din cele trei β 1. 4 1 0. 7 actiuni sunt subevauate, respectiv supraevaluate. Rezolvare: Folosind modelul CAPM se determină randamentul cerut, astfel:
II. 1. Acţiuni-aplicaţii rezolvate Conform modelului DDM cu o rată de creştere constantă preţul „corect” este: Concluzie: Comparând aceste preţuri teoretice cu cele de pe piaţă constatăm că actiunea A este subevaluată, iar actiunile B şi C sunt supraevaluate.
II. 1. Acţiuni-aplicaţii rezolvate Exemplul 2. Se anticipează ca la sfârşitul anului profitul firmei W să fie de 200. 000 u. m. Firma W are un capital social format din 100. 000 acţiuni, iar preţul bursier al unei acţiuni este de 50 u. m. Ce puteti spune despre anticiparile viitoare ale investitorilor, daca randamentul cerut de investitori este 10%? Rezolvare: Prin urmare, profitul pe acţiune estimat a se realiza la sfârşitul anului (E 1) este: E 1 = 200. 000 / 100. 000 = 2 u. m. Dacă randamentul cerut de investitori (k) este de 10% atunci valoarea prezentă a investiţiilor viitoare anticipată de investitori este de: Concluzii: • • Dacă investiţiile ce urmează a fi realizate de o firmă sunt percepute de investitori ca fiind fezabile (care să aducă un surplus de valoare firmei), atunci valoarea de piaţă a acţiunilor (a firmei) va creşte. Dacă investitorii anticipează că investiţia ce urmează să fie făcută de o firmă nu este una fezabilă, întrucât acestia anticipează o valoare actuală a investiţiei negativă, atunci preţul acţiunii pe piaţă va scădea înainte ca investiţia să fie făcută.
II. 1. Acţiuni-aplicaţii rezolvate Exemplul 3. Se încorporează 2/7 din rezervele unei companii şi se distribuie 4. 000 de titluri gratuite. Totalul rezervelor înainte de încorporare era de 1. 400. 000 u. m. , iar capitalul social era compus din 22. 500 acţiuni. Determinaţi valoarea dreptului de atribuire. Rezolvare: Se încorporează 2/7 x 1. 400. 000 = 400. 000 u. m corespunzător a 4. 000 titluri Valoarea nominală = 400. 000/4. 000 = 100
II. 1. Acţiuni - Aplicaţii propuse 1. Un analist financiar al Nomura Holdings Inc. analizează acţiunile a două companii de publicitate, respectiv WPP PLC şi New Motion Inc: Elemente tehnice WPP PLC β Preţ de piaţă Valoarea intrinsecă 1, 35 45 63 New Motion Inc 1, 15 30 ? Se ştie că rata dobânzii fără risc este 4, 5%, rentabilitatea pieţei este 14, 5% şi ultimul dividend acordat (D 0) de firma New Motion Inc a fost de 2, 23 u. m. /acţiune. Analistul financiar estimează o rată anuală de creştere a acestor dividende de 7% pentru următorii 10 ani, după care această rată este estimată la 3%. a) Estimaţi cursul acţiunii New Motion Inc. folosind modelul DDM cu rata de creştere constantă. b) Pe care din cele două acţiunile analizate aţi achiziţiona-o? c) Care sunt principalele dezavantaje ale modelului DDM cu rată de creştere constantă?
II. 1. Acţiuni - Aplicaţii propuse 2. France Telecom îşi majorează capitalul social prin emisiunea de noi acţiuni, raportul de subscripţie fiind de 4 acţiuni noi la 5 acţiuni vechi. Valoarea nominală a unei acţiuni FTE este 25, 3 €, iar prima de emisiune 1, 4 €. Ştiind că valoarea de piaţă a dreptului de preferinţă este 2, 5 € şi este cu 22, 5% mai mare decât cea teoretică, aflaţi care este ultimul curs cotat la EURONEXT al acţiunilor France Telecom? 3. Capitalul social al unei companii creşte cu 625. 000 u. m. prin emisiunea la paritate a 25. 000 de acţiuni. Capitalul social iniţial era de 1. 500. 000 u. m. , iar rezervele de 400. 000 u. m. Presupunând că rentabilitatea financiară este 9% şi sa menţinut constantă şi după majorare, iar un acţionar vechi deţine 2000 acţiuni, arătaţi cum se manifestă efectul de diluţie. 4. Care va fi opţiunea unei persoane de a investi dacă rata dobânzii pentru depozitele bancare este 14% în condiţiile în care pe piaţă există o acţiune cu valoare nominală de 500, prima de emisiune 15, iar pentru o acţiune nouă sunt necesare 5 drepturi de subscriere care cotează la bursa la 8?
II. 2. Obligaţiuni • Obligaţiunile: parte dintr-un împrumut • Caracteristici: - Investiţii pe termen mediu şi lung Creanţa deţinătorului asupra emitentului Angajamentul de plată al creditorului Mai mulţi creditori Titlu negociabil Registrul acţionarilor • Elementele împrumutului obligatar: - Valoarea nominală Valoarea de subscriere Cuponul de dobândă Rata cuponului (rata nominală) Rata netă de dobândă Dobânda acumulată Termenul de rambursare Modalitatea de rambursare Rambursarea anticipată Costul rambursării Costul emisiunii şi al împrumutului Cursul
II. 2. Obligaţiuni • - Obligaţiuni: Garantate - Prin ipotecă - Prin drept de gaj Negarantate Obligaţiuni: Corporative Emise de stat şi autorităţi locale • - Obligaţiuni corporative: Cu ipotecă prioritară Cu gaj asupra valorilor mobiliare sau activelor Garantate cu active Cu opţiune de răscumpărare din partea emitentului (Call bond) Cu opţiune de răscumpărare din partea investitorului (Put bond) Convertibile Cu rată nominală a dobânzii variabilă Care inversează variaţia ratei dobânzii Plătibile în obligaţiuni De catastrofă Indexate • -
II. 2. Obligaţiuni • - Titluri de stat: Obligaţiuni publice (T-bond) Bonuri de tezaur (T-notes) Bilete de trezorerie (T-bills) • Obligaţiuni municipale: - Generale - Cu venit • - Pe termen scurt: Note anticipative de impozite Note anticipative de venit Note anticipative de obligaţiuni
Teste de autoevaluare 1. 2. 3. Care din afirmaţiile următoare referitoare la analiza tehnică a unei acţiuni nu este adevărată: a) oferă posibilitatea proiectării în viitor a comportamentului trecut şi actual al cursului titlurilor; b) necesită trasarea unei drepte suport obţinută prin unirea punctelor indicând cel mai ridicat nivel al cursului; c) furnizează semnal de vânzare în cazul în care configuraţia este în M; d) se bazează pe premisa potrivit căreia evoluţia preţurilor valorilor mobiliare urmează scheme constante; e) sub forma configuraţiei în triunghi ascendent, evidenţiază o puternică creştere a cursurilor, dând semnal de cumpărare. Politica ratelor în distribuirea de dividende presupune: a) stabilirea de către conducerea societăţii a unui procent de repartizare a dividendelor ce va fi aplicat asupra profitului net obţinut de societatea respectivă; b) satisfacerea cu prioritate, din profitul net obţinut, a necesităţilor de autofinanţare; c) apelarea la rezerve constituite anterior (în cazul în care profitul obţinut nu este suficient) pentru păstrarea trendului crescător al dividendului; d) realizarea unei creşteri foarte reduse a dividendului acordat de la un an la altul; e) existenţa unui surplus din profitul net al societăţii, după acoperirea resurselor necesare creşterii fondurilor proprii ale societăţii. Alegeţi afirmaţia corectă dintre cele enumerate mai jos: a) acţiunile preferenţiale dau dreptul la dividend calculat asupra profitului distribuibil după plata dividendului aferent acţiunilor comune; b) acţiunile preferenţiale nu pot avea un nivel fix şi prestabilit al dividendului datorită fluctuaţiei mărimii profitului obţinut de către societate; c) nivelul dividendului reprezintă suma ce se determină şi trebuie plătită la începutul unui exerciţiu financiar; d) dacă rata dividendului este exprimată procentual, determinarea dividendului aferent se face prin aplicarea procentului la valoarea de piaţă a acţiunii; e) acţiunile de trezorerie nu sunt purtătoare de dividende.
Teste de autoevaluare 4. 5. 6. Despre drepturile preferenţiale (de subscriere şi de atribuire) se afirmă: a) pot fi considerate valori mobiliare; b) dau dreptul posesorului să achiziţioneze titluri primare; c) pot fi repartizate atât acţionarilor deţinători de acţiuni comune, cât şi celor deţinători de acţiuni preferenţiale; d) nu pot fi tranzacţionate pe piaţa secundară de capital; e) au durată de viaţă limitată. Care afirmaţie nu este corectă? Dividendul net pe acţiune se calculează în funcţie de: a) randamentul plasamentului; b) profitul net repartizat acţionarilor; c) profitul brut obţinut; d) rentabilitatea cerută de acţionari; e) coeficientul multiplicator al capitalului. În cazul majorării capitalului unei societăţi prin încorporarea unei părţi din rezerve: a) acţiunile se vând pe piaţă, contravaloarea acestora fiind încasată de societatea emitentă; b) are loc o modificare substanţială a capitalului propriu al societăţii respective care va înregistra o creştere; c) imediat după majorare, acţiunile societăţii respective înregistrează o creştere a cursului; d) se produce o redivizare a capitalului propriu (între capitalul social şi rezerve); e) preţul de emisiune al noilor acţiuni este în general mai mare decât valoarea nominală a acestora.
Teste de autoevaluare - răspunsuri 1–B 2–A 3–E 4–D 5–B 6–D
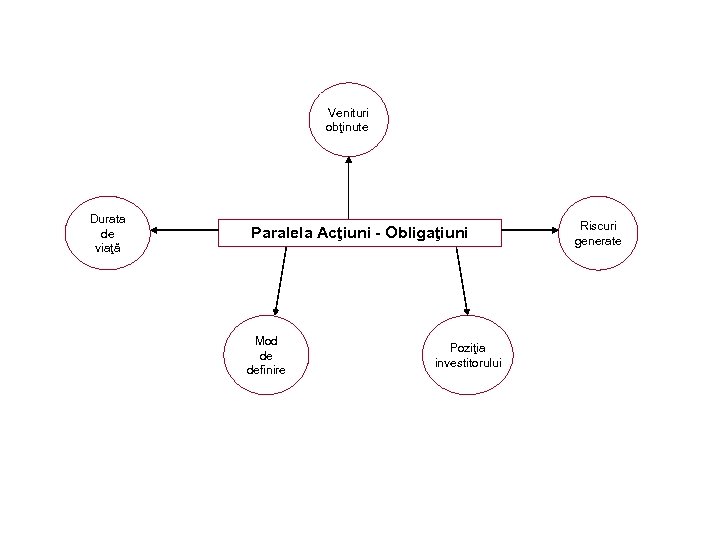Venituri obţinute Durata de viaţă Paralela Acţiuni - Obligaţiuni Mod de definire Poziţia investitorului Riscuri generate
II. 2. Obligaţiuni – aplicaţii rezolvate Exemplul 1. Presupunem că o obligaţiune are valoarea nominală VN =1000 RON, rata cuponului (c) este 10%, scadenţa (n) este 5 ani, iar rata dobânzii (y) este 8%. Care ar fi preţul obligaţiunii? Rezolvare: Am enunţat mai sus că acesta este o valoare prezentă a cash-flow-urilor viitoare. Cash flow-urile sunt formate din cupoanele din anul 1 până în anul 4 şi cupon plus valoarea nominală în anul 5 (vezi figura de mai jos). C 1=100 RON 0 1 C 2=100 RON C 3=100 RON C 4=100 RON 2 3 4 În exemplul nostru, preţul obligaţiunii clasice va fi: C 5+VN=1100 RON 5
II. 2. Obligaţiuni – aplicaţii rezolvate Exemplul 2. Presupunem că un investitor vinde o obligaţiune la data de 15 februarie N, care următoarele caracteristici: valoarea nominală 10. 000 USD, rata cuponului este 5, 5%, iar cupoanele sunt semianuale, scadenţa este la momentul N+3. Ştiind că ultimul încasat a fost la 31 ianuarie N, obligaţiunea se rambursează la scadenţă, iar rata dobânzii de pe piaţă este 8%, să se determine dirty price (DP), clean price (CP) şi accrued interest (AI). 15 feb N 31 ian N C 1 C 2 31 iul N 31 ian N+1 C 3 31 iul N+1 C 4 C 5 31 ian N+2 31 iul N+3 C 6 +VN 31 ian N+3 Rezolvare: Observăm faptul că perioada de timp între ultimul cupon încasat (31 ianuarie N) şi data vânzării (15 februarie N) obligaţiunii este de 15 zile, de aceea, vânzătorului titlului i se cuvine acea parte din cupon aferente acestei perioade de 15 zile. Pentru a determina preţul obligaţiunii la momentul zero, adică 15 februarie N, vom folosi cash-flow-urile viitoare, respectiv cuponul de la 31 iulie N până la 31 ianuarie N+3, şi valoarea nominală de la 31 ianuarie N+3.
II. 2. Obligaţiuni – aplicaţii rezolvate Observatii! 1. Observăm faptul că folosim valoarea întregului cupon de la 31 iulie N (C 1) pentru a determina preţul obligaţiunii, deşi cumpărătorului nu i se cuvine întregul cupon, de aceea, spunem că preţul determinat este un preţ brut. 2. În preţul brut este inclusă, deci, dobânda acumulată, pe care cumpărătorul o datorează vânzătorului obligaţiunii. Prin urmare, deşi la 31 iulie N cumpărătorul încasează întreaga valoarea a cuponului C 1, întrucât el a plătit dobânda acumulată la achiziţionarea obligaţiunii, rămâne practic doar cu diferenţa între C 1 şi AI.
II. 2. Obligaţiuni – aplicaţii rezolvate Exemplul 3. Dacă preţul de pe piaţă al unei obligaţiuni este în prezent 1134, 2 GBP şi are următoarele caracteristici: valoarea nominală este 1000 GBP, rata cuponului este 10%, scadenţa 10 ani, iar modalitatea de rambursare este la maturitate. Cât este randamentul la maturitate? Rezolvare: Rezolvând ecuaţia de gradul 10 de mai sus, s-a obţinut o soluţie reală pozitivă egală cu 8%, o soluţie reală negativă şi 8 soluţii ce aparţin mulţimii numerelor complexe. Folosind formula prin care se aproximeaza randamentul, acesta va fi: • • unde: n reprezintă numărul de ani rămăşi până la scadenţă. Randamentul aproximat pentru exemplul de mai sus este 8, 11%.
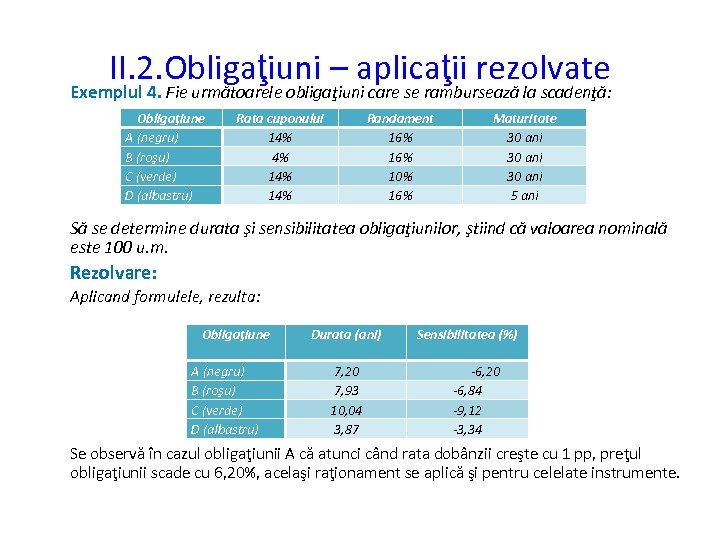II. 2. Obligaţiuni – aplicaţii rezolvate Exemplul 4. Fie următoarele obligaţiuni care se rambursează la scadenţă: Obligaţiune A (negru) B (roşu) C (verde) D (albastru) Rata cuponului 14% 4% 14% Randament 16% 10% 16% Maturitate 30 ani 5 ani Să se determine durata şi sensibilitatea obligaţiunilor, ştiind că valoarea nominală este 100 u. m. Rezolvare: Aplicand formulele, rezulta: Obligaţiune A (negru) B (roşu) C (verde) D (albastru) Durata (ani) 7, 20 7, 93 10, 04 3, 87 Sensibilitatea (%) -6, 20 -6, 84 -9, 12 -3, 34 Se observă în cazul obligaţiunii A că atunci când rata dobânzii creşte cu 1 pp, preţul obligaţiunii scade cu 6, 20%, acelaşi raţionament se aplică şi pentru celelate instrumente.
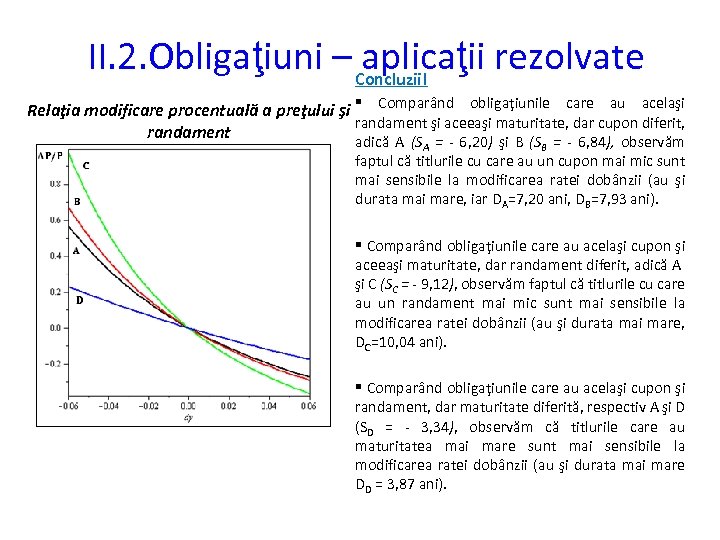II. 2. Obligaţiuni – Concluzii! aplicaţii rezolvate Relaţia modificare procentuală a preţului şi § Comparând obligaţiunile care au acelaşi randament şi aceeaşi maturitate, dar cupon diferit, randament adică A (S = - 6, 20) şi B (S = - 6, 84), observăm A B faptul că titlurile cu care au un cupon mai mic sunt mai sensibile la modificarea ratei dobânzii (au şi durata mai mare, iar DA=7, 20 ani, DB=7, 93 ani). § Comparând obligaţiunile care au acelaşi cupon şi aceeaşi maturitate, dar randament diferit, adică A şi C (SC = - 9, 12), observăm faptul că titlurile cu care au un randament mai mic sunt mai sensibile la modificarea ratei dobânzii (au şi durata mai mare, DC=10, 04 ani). § Comparând obligaţiunile care au acelaşi cupon şi randament, dar maturitate diferită, respectiv A şi D (SD = - 3, 34), observăm că titlurile care au maturitatea mai mare sunt mai sensibile la modificarea ratei dobânzii (au şi durata mai mare DD = 3, 87 ani).
II. 2. Obligaţiuni – aplicaţii propuse 1. Fie o obligaţiune cu valoarea nominală 1000 RON, rata cuponului 10%, scadenţa 10 ani, iar modalitatea de rambursare este la scadenţă. Să se determine preţul obligaţiunii dacă randamentul devine 8%, folosind: a). formula de calcul a preţului şi b). pornind de la modificarea procentuală a preţului folosind durata. Raspuns: a) P 1=1134, 2016 RON; b) P 1=1228, 9 RON 2. Valoarea nominală a unei obligaţiuni este 1000 u. m. Ştiind că obligaţiunea se rambursează în anuităţi constante în valoare de 100 u. m. şi că rata cuponului este de 6, 66%, determinaţi: a) Scadenţa obligaţiunii, dacă preţul de piaţă al unei obligaţiuni este egal cu valoarea sa nominală. b) Rata aferentă anului 2 şi preţul obligaţiunii, în ipoteza că scadenţa este 35 ani. 3. a) Determinaţi randamentul la maturitate al unei obligaţiuni cu scadenţa 2 ani, valoare nominală de 1000 u. m. (rambursarea se face la scadenţă), rata cuponului 10 % (dobanda se plăteşte anual) şi preţ de piaţă 966, 1989 u. m. b). Determinaţi randamentul folosind formula simplificată.
II. 2. Obligaţiuni – aplicaţii propuse 4. Despre o obligatiune se cunosc următoarele: scadenţa este de n ani, valoarea nominală este VN, rambursarea se face in rate anuale constante R, rata cuponului creşte in fiecare an cu p puncte procenuale (prima rata a cuponului fiind de c 1 %). a) Deduceti o formulă pentru cuponul la momentul t (Dt). b) Calculaţi D 15 dacă VN=1000 u. m. , n=20 ani, p=0. 25 puncte procentuale, c 1=10%. c) Cât este preţul acestei obligaţiuni? 5. O obligaţiune se caracterizează prin următoarele: valoare nominală de 1000 u. m. , o rată a cuponului de 10% şi scadenţă peste 3 ani, randamentul la maturitate este 8%. Se cere: a) Să se calculeze durata obligaţiunii; b) Randamentul la maturitate devine 6%, să se determine noul preţ al obligaţiunii utilizând două metode de calcul (utilizând durata şi prin metoda clasică). c) Să se determine preţul obligaţiunii utilizând convexitatea.
II. Instrumente financiare-bibliografie • Anghelache G. , “Piaţa de capital: caracteristici, evoluţii, tranzacţii”, Ed. Economică, Bucureşti, 2004 • Anghelache G. şi colectiv, “Pieţe de capital şi tranzacţii bursiere” – aplicaţii şi studii de caz, Ed. Economică, Bucureşti, 2003 • Bodie, Z. , A. Kane, and A. J. Marcus (2007), Essentials of Investments, 6 th edition, Mc. Graw Hill International Edition
III. Tranzacţii bursiere • Cuprinsul unitatii de invatare 3: - Definirea tranzactiilor bursiere…… ………. . pag 56 Tranzactii la vedere. …………. . . …pag 57 Tranzactii in marja. ………………. pag 58 Tranzactii la termen……. . ……………. . …. …pag 59 Aplicatii rezolvate……………. …. pag 60 Aplicatii propuse……………. . . …. pag 62 Bibliografie…………………. pag 63
III. Tranzacţii bursiere • Obiectivele unității de învățare III: - familiarizarea cu tipurile de pieţe în cadrul cărora se pot realiza tranzacţii - cunoaşterea tipurilor de tranzacţii care se pot efectua pe piaţa de capital şi înţelegerea modului în care acestea funcţionează
III. Tranzacţii bursiere • Toate contractele de vânzare-cumpărare de titluri sau alte active • În funcţie de momentul executării contractului: - cu lichidare imediată cu lichidare normală la termen - cash în marjă - operaţiuni simple de investire operaţiuni de arbitraj operaţiuni speculative operaţiuni de acoperire operaţiuni cu caracter tehnic • În funcţie de natura contului deschis la broker: • În funcţie de scopul tranzacţiei:
III. Tranzacţii bursiere • TRANZACTII LA VEDERE • Tranzacţii spot, cash sau pe bani gata • Iniţiatorul îşi asumă obligaţia pentru titlurile vândute sau pentru contravaloarea titlurilor cumpărate • Tipuri de piaţă: - Regular - Odd Lot - Pieţe cu iniţiere: - Buy In - Sell Out
III. Tranzacţii bursiere • • TRANZACTII IN MARJA Vânzări scurte sau cumpărări de pe poziţia descoperit Variantă tranzacţiilor la vedere, dar bazate pe credit de la broker Avantaj: capacitate suplimentară de finanţare: • • Brokerul percepe o dobândă Contul în marjă Titlurile sunt păstrate drept garanţie Operaţiunea este marcată zilnic la piaţă • - Tipuri de marjă: Marja iniţială Marja de menţinere (permanentă) Marja curentă Marja absolută Marja returnabilă
III. Tranzacţii bursiere • TRANZACTII LA TERMEN • Caracteristicile tranzacţiei se stabilesc în prezent, dar finalizarea ei se va realiza la o dată ulterioară • Tranzacţiile la termen: - Tranzacţii la termen ferm - Tranzacţii la termen condiţionate • Pentru cele mai lichide valori mobiliare: contracte standardizate ! Instrumentele pieţei de capital: primare (acţiuni, obligaţiuni, drepturi); derivate (futures, opţiuni, CFD); sintetice (indici) ! Tranzacţii: la vedere (cash, marjă); la termen (futures, forward, opţiuni) ! Tranzacţii pe pieţele bursiere (futures, opţiuni); de negociere (forward, opţiuni)
III. Tranzacţii bursiere- aplicatii rezolvate Exemplul 1. Un investitor cumpara 100 de actiuni X la un curs de 2, 450 u. m. /actiune. Pana in ziua de lichidare a lunii respective, cursul actiunii va creste, iar la o data situata intre data cumpararii actiunilor si cea de lichidare, cursul devine 2, 600 u. m. /actiune. Investitorul decide sa vanda actiunile. Care va fi rezultatul pentru investitor in conditiile unei taxe de negociere de 0, 5% ? Rezolvare: Valoarea tranzactiei de cumparare = 100 * 2, 450 = 245 Taxa de negociere pentru tranzactia de cumparare = 245 * 0, 5% = 1, 225 Valoarea tranzactiei de vanzare = 100 * 2, 600 = 260 Taxa de negociere pentru tranzactia de vanzare = 260 * 0, 5% = 1, 3 Rezultatul final = - (245 +1, 225) + (260 – 1, 3) = 12, 475
III. Tranzacţii bursiere- aplicatii rezolvate Exemplul 2: Un investitor detine suma de 100. 000 si doreste sa achizitioneze 500 de actiuni X la un curs de 1, 200 u. m. /actiune. Broker-ul practica o dobanda de 10% pe an. Daca pe parcursul lunii cursul devine: I) 1, 300 u. m. /actiune II) 1, 100 u. m. /actiune Se cere rezultatul tranzactiei pentru investitor: Rezolvare: I) Valoarea tranzactiei de cumparare = 500 * 1, 2 = 600 Datoria la broker = 600 – 100 = 500 Dobanda la credit = 500 * 10% * 1/12 = 4, 167 Valoarea tranzactiei de vanzare = 500 * 1, 3 = 650 Rezultatul final = 650 -600 -4, 167=45, 833 II) Valoarea tranzactiei de cumparare = 500 * 1, 2 = 600 Datoria la broker = 600 – 100 = 500 Dobanda la credit = 500 * 10% * 1/12 = 4, 167 Valoarea tranzactiei de vanzare = 500 * 1, 100 = 550 Rezultatul final = 550 - 600 – 4, 167 = -54, 167
III. Tranzacţii bursiere- aplicatii propuse Un investitor doreste sa cumpere 200 de actiuni, la un curs de 65 u. m. /actiune, la termen de o luna, in conditiile unei marje de 30% si a unei dobanzi practicate de broker de 14%/an. Actiunile vor fi vandute cu 72, 5 u. m. /actiune. Cat este rata profitului obtinut pentru investitor?
III. Tranzacţii bursiere - bibliografie • Anghelache G. , “Piaţa de capital: caracteristici, evoluţii, tranzacţii”, Ed. Economică, Bucureşti, 2004 • Anghelache G. şi colectiv, “Pieţe de capital şi tranzacţii bursiere” – aplicaţii şi studii de caz, Ed. Economică, Bucureşti, 2003 • Bodie, Z. , A. Kane, and A. J. Marcus (2007), Essentials of Investments, 6 th edition, Mc. Graw Hill International Edition
IV. Instrumente financiare derivate • Cuprinsul unitatii de invatare 4: - Contracte forward……………. . pag 66 Contracte futures…. . …………. . . …pag 67 Optiuni……………. . ………………. pag 68 Aplicatii rezolvate……………. …. pag 71 Aplicatii propuse……………. . . …. pag 84 Bibliografie…………………. pag 87
IV. Instrumente financiare derivate • Obiectivele unității de învățare IV: - definirea instrumentelor financiare derivate - analiza modului în care acestea se pot utiliza - avantajele şi riscurile utilizării instrumentelor financiare derivate
IV. Instrumente financiare derivate Contracte forward • Contracte nestandardizate • Acord ferm între cumpărător şi vânzător • Cumpărătorul de contract forward: cumpără activul suport • Vânzătorul de contract forward: vinde activul suport • Scop: eliminarea incertitudinii legate de evoluţia preţurilor • Rezultatul: Long: Curs la scadenţă – Preţ din contract Short: Preţ din contract – Curs la scadenţă
IV. Instrumente financiare derivate Contracte futures • Contracte standardizate • Caracteristicile: - Standardizarea activului suport şi a cantităţii tranzacţionate - Termenul de executare - Preţul contractului - Marcarea la piaţă - Limita de fluctuaţie a preţului - Lichidarea
IV. Instrumente financiare derivate Contracte de optiuni • Contracte care oferă cumpărătorului dreptul dar nu şi obligaţia de a achiziţiona sau a vinde un anumit suport, la un preţ stabilit în contract şi contra unei sume plătite iniţial • În funcţie de poziţia cumpărătorului faţă de activul suport: - Opţiuni de cumpărare (call) - Opţiuni de vânzare (put) • În funcţie de momentul exercitării: - Opţiuni europene - Opţiuni americane • În funcţie de piaţa pe care se tranzacţionează contractul: - Opţiuni standardizate - Opţiuni nestandardizate
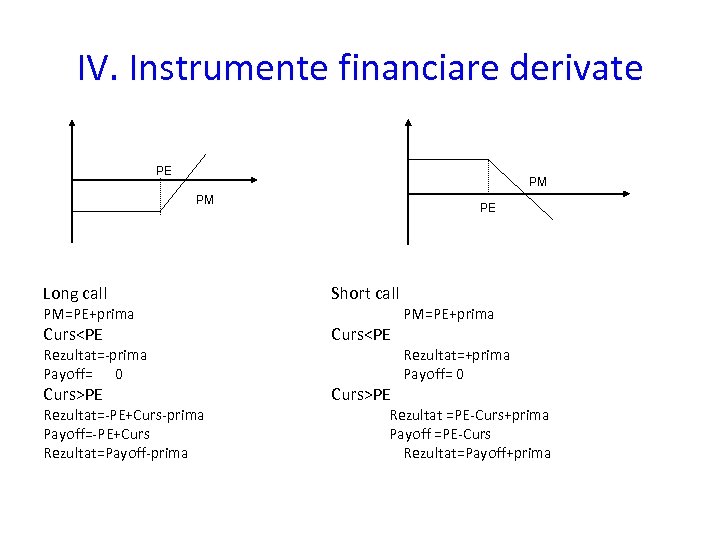IV. Instrumente financiare derivate PE PM PM PE Long call Short call Curs
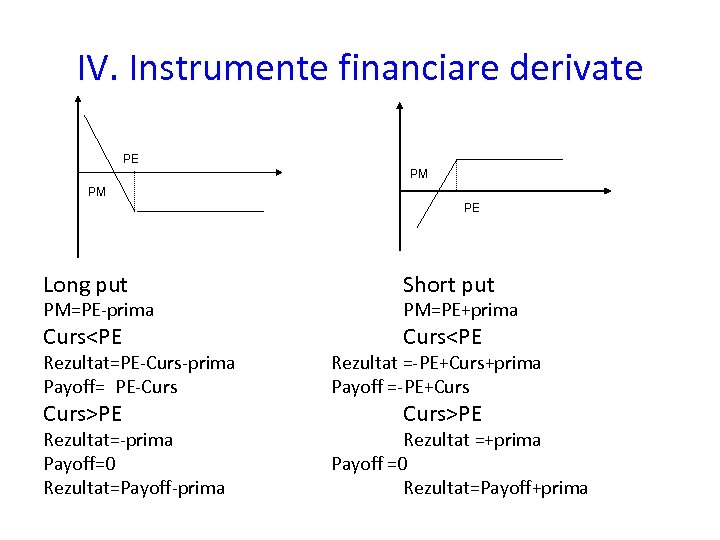IV. Instrumente financiare derivate PE PM PM PE Long put Short put Curs
IV. Instrumente financiare derivate– aplicatii rezolvate-Contracte futures Marcarea la piaţă Exemplul 1. Un investitor tranzactionează un contract avand ca activ suport acţiunea ABC. Marja iniţială este 900 RON/contract, iar marja de menţinere 675 RON/contract. Presupunem că la 3 martie 2008, un investitor achiziţionează 2 contracte futures cu suport acţiunea ABC, în momentul iniţial preţul futures cu scadenţa decembrie 2008 este 3 RON. Dimensiunea unui contract este de 1000 de acţiuni ABC. Să se arate cum se realizează marcarea la piaţă a contractelor futures. Rezolvare:
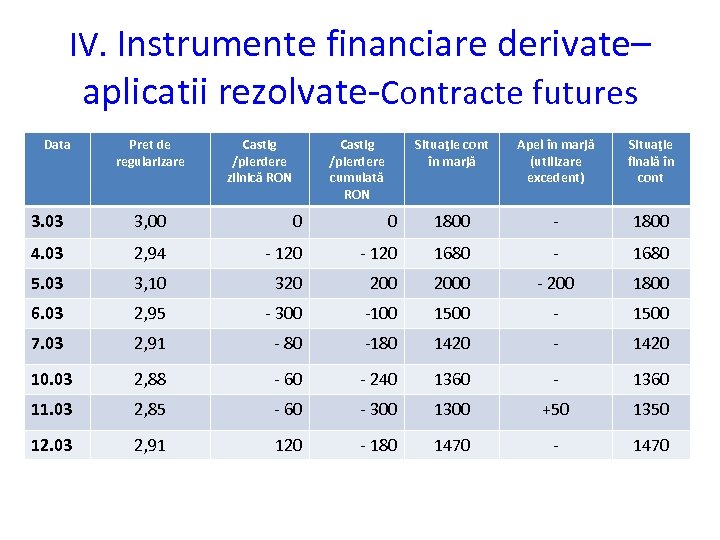IV. Instrumente financiare derivate– aplicatii rezolvate-Contracte futures Data Pret de regularizare Castig /pierdere zilnică RON Castig /pierdere cumulată RON Situaţie cont în marjă Apel în marjă (utilizare excedent) Situaţie finală în cont 3. 03 3, 00 0 0 1800 - 1800 4. 03 2, 94 - 120 1680 - 1680 5. 03 3, 10 320 2000 - 200 1800 6. 03 2, 95 - 300 -100 1500 - 1500 7. 03 2, 91 - 80 -180 1420 - 1420 10. 03 2, 88 - 60 - 240 1360 - 1360 11. 03 2, 85 - 60 - 300 1300 +50 1350 12. 03 2, 91 120 - 180 1470 - 1470
IV. Instrumente financiare derivate–aplicatii rezolvate. Contracte futures § La 4. 03, rezultatul investitorului pentru cele două contracte futures va fi: Rezultat = (preţ de regularizare la 4 mart – preţ de regularizare la 3 mart)*mărimea contractului * nr. contracte Rezultat = (2, 94 RON/acţiune – 3 RON/acţiune) * 1000 actiuni/contract* 2 contracte= -120 RON § La 12. 03, rezultatul investitorului pentru cele două contracte futures va fi: Rezultat = (preţ futures la scadenţă – preţ futures la t 0) * mărimea contractului * nr. contracte Rezultat = (2, 91 RON/acţiune – 3 RON/acţiune) * 1000 actiuni/contract 2 contracte= -180 RON sau Rezultat = (Sold final – Sold iniţial) + (Retrageri - Depuneri)= = (1470 RON – 1800 RON) + (200 RON – 50 RON) = - 180 RON
IV. Instrumente financiare derivate– aplicatii rezolvate-Contracte futures Hedging cu contracte futures Exemplul 2. Un investitor a realizat o operaţiune de short selling (vânzare • • scurtă; opusul tranzacţiilor în marjă) pe 1000 de acţiuni SIF 1 la cursul S 0 = 1, 5 RON/acţiune. Pentru a se proteja împotriva riscului de creştere a cursului acestora tranzacţionează un contract futures având activ suport SIF 1, scadenţa peste 6 luni, dimensiunea unui contract este de 1000 acţiuni. Preţul futures iniţial F 0= 1, 6 RON/acţiune. Cu 1 lună înainte de scadenţă investitorul îşi lichidează contractele, determinaţi rezultatul acestuia ştiind că: a) S 5 M=1, 55 RON/acţiune, F 5 M=1, 65 RON/acţiune; b) S 5 M=1, 4 RON/acţiune, F 5 M=1, 5 RON/acţiune. Rezolvare: Risc de creştere a cursului SIF 1 long futures a) Rezultat în spot = (S 0 – ST) * 1000 acţiuni = (1, 50 RON/acţiune – 1, 55 RON/ acţiune) * 1000 acţiuni = - 50 RON Rezultat în futures = (FT –F 0) * 1000 acţiuni = (1, 65 RON/acţiune – 1, 60 RON/acţiune) * 1000 acţiuni = 50 RON Rezultat total = 0 RON (hedging perfect)
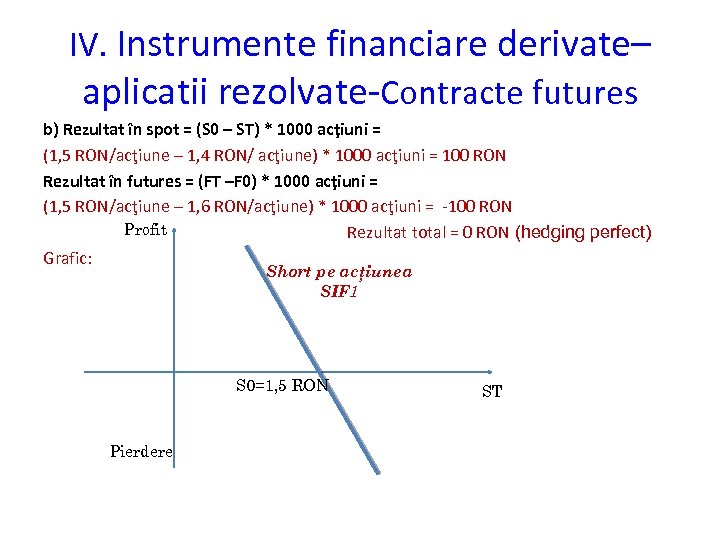IV. Instrumente financiare derivate– aplicatii rezolvate-Contracte futures b) Rezultat în spot = (S 0 – ST) * 1000 acţiuni = (1, 5 RON/acţiune – 1, 4 RON/ acţiune) * 1000 acţiuni = 100 RON Rezultat în futures = (FT –F 0) * 1000 acţiuni = (1, 5 RON/acţiune – 1, 6 RON/acţiune) * 1000 acţiuni = -100 RON Profit Rezultat total = 0 RON (hedging perfect) Grafic: Short pe acţiunea SIF 1 S 0=1, 5 RON Pierdere ST
IV. Instrumente financiare derivate–aplicatii rezolvate Strategii cu optiuni. Straddle § § • • • Una din cele mai cunoscute tipuri de strategii este straddle. Această strategie poate fi creată tranzacţionând o opţiune call pe activul financiar la un preţ de exerciţiu PE 1 şi cumpărând o opţiune put pe acelaşi suport şi la acelaşi preţ de exerciţiu PE 1. Cele două opţiuni au aceeaşi scadenţă. Profitul întregii strategii este suma profiturilor date de compunerea celor poziţii. Exemplul 1. Se cumpără un straddle pentru 100 de acţiuni X. Preţul de exercitare este 11 u. m. /acţiune, prima CALL este egală cu prima PUT şi este de 0, 4 u. m. /acţiune. La scadenţă, cursul de piaţă al acţiunii X este: I) 10 u. m. /acţiune II) 10, 40 u. m. /acţiune III) 11 u. m. /acţiune IV)11, 2 u. m. /acţiune V) 12, 3 u. m. /acţiune Rezultatul operatorului în cele cinci situaţii este:
IV. Instrumente financiare derivate–aplicatii rezolvate. Strategii cu optiuni. Straddle Rezolvare: PE PRput PRcall Dacă PE > curs se exercită opţiunea PUT se vinde la preţ de exerciţiu, se cumpără la curs, se plăteşte suma primelor Daca PE = curs strategia se abandonează; pierderea este maximă şi este egală cu suma primelor plătite Daca PE < curs se exercită opţiunea CALL se cumpără la preţ de exerciţiu, se vinde la curs, se plăteşte suma primelor PRput = prag de rentabilitate PUT = PE – suma primelor = 11 – 0, 80 = 10, 2 PRcall = prag de rentabilitate CALL = PE + suma primelor = 11 + 0, 80 = 11, 8 I)1. 000 < 1. 100 Rezultatul = 100 * (11 – 10 – 0, 8) = 20 II)1. 040 < 1. 100 Rezultatul = 100* (11 – 10, 4 – 0, 8) = -20 III)1. 100 = 1. 100 Rezultatul = 100 * (-0, 8) = -80 IV)1. 120 > 1. 100 Rezultatul=100*(-11 + 11, 2 – 0, 8) = -60 V)1. 230 > 1. 100 Rezultatul = 100*(-11 + 12, 3 – 0, 8) = -50
IV. Instrumente financiare derivate–aplicatii rezolvate- Strategii cu optiuni. Straddle • Exemplul 2 Se vând doua straddle cu preţ de • • • exerciţiu de 180 u. m. /acţiune, prima put de 4 u. m. /acţiune si prima call 6 u. m. /acţiune. La scadenţă, cursul de piaţă este: I)160 u. m. /acţiune II)172 u. m. /acţiune III)180 u. m. /acţiune IV)185 u. m. /acţiune V)240 u. m. /acţiune Rezultatul înregistrat de operator este:
IV. Instrumente financiare derivate–aplicatii rezolvate- Strategii cu optiuni. Straddle PRput PRcall PE Dacă PE > curs se exercită opţiunea PUT se cumpără la preţ de exerciţiu, se vinde la curs, se âncasează suma primelor Daca PE = curs strategia se abandonează; câştigul este maxim şi este egal cu suma primelor Daca PE < curs se exercită opţiunea CALL se vinde la preţ de exerciţiu, se cumpără la curs, se încasează suma primelor PRput = prag de rentabilitate PUT = PE – suma primelor = 180 – 100 = 170 PRcall = prag de rentabilitate CALL = PE + suma primelor = 180 + 10 = 190 I)160 < 180 Rezultatul = 200 * (-180 + 160 + 10) = -2. 000 II)172 < 180 Rezultatul = 200 * (-180 + 172 + 10) = 400 III)180 = 180 Rezultatul = 200 *10 = 2. 000 IV)185 > 180 Rezultatul = 200 * (180 - 185 + 10) = 1. 000 V)240 > 180 200 * (180 - 240 + 10) = -10. 000
IV. Instrumente financiare derivate–aplicatii rezolvate Strategii cu optiuni. Strangle • • Una din cele mai cunoscute tipuri de strategii este strangle. Această strategie poate fi creată tranzacţionând o opţiune call pe activul financiar la un preţ de exerciţiu PE 1 şi cumpărând o opţiune put pe acelaşi suport şi la acelaşi preţ de exerciţiu PE 2, mai mare. Cele două opţiuni au aceeaşi scadenţă. Profitul întregii strategii este suma profiturilor date de compunerea celor poziţii. Exemplul 3 Se cumpără un strangle la preţ de exercitare pentru opţiunea CALL de 7, 5 u. m. /acţiune şi preţ de exercitare pentru opţiunea PUT de 6 u. m. /acţiune. Prima CALL este 0, 3 u. m. /acţiune, iar prima PUT este 0, 2 u. m. /acţiune. La scadenţă cursul este: I)5, 4 u. m. /acţiune II)5, 8 u. m. /acţiune III)6, 8 u. m. /acţiune IV)7, 7 u. m. /acţiune V)8, 3 u. m. /acţiune Rezultatul operatorului în cele cinci situaţii este:
IV. Instrumente financiare derivate–aplicatii rezolvate Strategii cu optiuni. Strangle PEp ut PRp ut PEcall PRput = prag de rentabilitate PUT = PEput – suma primelor = 6 – 0, 5 = 5, 5 PRcall = prag de rentabilitate CALL = PEcall + suma primelor = 7, 5 + 0, 5 = 8 Daca PEput > curs se exercită opţiunea PUT se vinde la preţ de exerciţiu PUT, se cumpără la curs, se plăteşte suma primelor Daca PEput < curs < Pecall contractul se abandonează; pierderea este maximă şi este egală cu suma primelor plătite Daca PEcall < curs se exercită opţiunea CALL se cumpără la preţ de exerciţiu CALL, se vinde la curs, se plăteşte suma primelor I)5. 400 < 6. 000 Rezultatul=100*(6. 000 – 5. 400 – 500)=10. 000 II)5. 800 < 6. 000 Rezultatul=100*(6. 000 – 5. 800 – 500)=-30. 000 III)6. 000 < 6. 800 < 7. 500 Rezultatul = 100 * (-500) = -50. 000 IV)7. 700 > 7. 500 Rezultatul=100*(-7. 500 + 7. 700 – 500)=-30. 000 V)8. 300 > 7. 500 Rezultatul=100*(-7. 500 + 8. 300 – 500)=30. 000
IV. Instrumente financiare derivate–aplicatii rezolvate - Strategii cu optiuni. Strangle • Exemplul 4 Se vinde un strangle pentru 200 de acţiuni, la preţ de exercitare PUT de 115 u. m. /acţiune, preţ de exercitare CALL de 150 u. m. /acţiune, prima CALL de 6 u. m. /acţiune şi prima PUT de 5 u. m. /acţiune. La scadenţă, cursul acţiunii este: • I)100 u. m. /acţiune • II)110 u. m. /acţiune • III)140 u. m. /acţiune • IV)155 u. m. /acţiune • V)162 u. m. /acţiune • Rezultatul operatorului este:
IV. Instrumente financiare derivate–aplicatii rezolvate - Strategii cu optiuni. Strangle PRca PRp ut ll PEpu t PEca ll PRput = prag de rentabilitate PUT = PEput – suma primelor = 115 – 11 = 104 PRcall = prag de rentabilitate CALL = PEcall + suma primelor = 150 + 11 = 161 Daca PEput > curs se exercită opţiunea PUT se cumpără la preţ de exerciţiu PUT, se vine la curs, se încasează suma primelor Daca PEput < curs < Pecall contractul se abandonează de către cumpărător; câştigul pentru vânzător este maxim şi este egal cu suma primelor încasate Daca PEcall < curs se exercită opţiunea CALL se vinde la preţ de exerciţiu CALL, se cumpără la curs, se încasează suma primelor I)1. 000 < 1. 150 Rezultatul = 100*(-1. 150 + 1. 000 + 110)= -4. 000 II)1. 100 < 1. 150 Rezultatul = 100*(-1. 150 + 1. 100 + 110)= 6. 000 III)1. 150 < 1. 400 < 1. 500 Rezultatul = 100 * 110 = 11. 000 IV)1. 550 > 1. 500 Rezultatul=100*( 1. 500 – 1. 550 + 110) = 6. 000 V)1. 620 > 1. 500 Rezultatul=100*(1. 500 – 1. 620 + 110) = -1. 000
Instrumente financiare derivate - Aplicatii propuse 1. Se cumpără doua optiuni PUT, una de tip european şi alta de tip american, ambele având preţul de exerciţiu de 23, 400 si scadenţa la tn. Prima opţiunii de tip european este de 1, 500, iar cea a opţiunii de tip american este de 1, 800. Care este cel mai mare profit cumulat al operatorului, dacă pe piaţă se înregistrează următoarele cursuri ale activului suport: la t 1: 23, 00; la t 2: 24, 95; la t 3: 20, 90; la t 4: 19, 50; la t 5: 22, 40 NOTA: Opţiunile de tip european se exercită la scadenţă, iar opţiunile de tip american se exercită la scadenţă sau oricând până la scadenţă. 2. Se vând 5 opţiuni CALL. Cursul actual al activului suport este de 13, preţul de exerciţiu este de 14, 4, prima este 1, iar rezultatul la scadenţă al operatorului este o pierdere de 450. Care este cursul activului suport la scadenţă? 3. O opţiune CALL pe acţiunea X cu scadenţa peste o lună şi preţul de exerciţiu 50 u. m. valorează în prezent 10, 4142 u. m. Ştiind că acţiunea X se tranzacţionează în prezent la 55 u. m. şi că rata dobânzii este de 10%, să se determine rezultatul la scadenţă al unei opţiuni PUT (poziţie long) cu aceeaşi scadenţă, acelaşi activ suport şi preţ de exerciţiu, dacă după o lună cursul acţiunii X devine: a. 51 u. m. , b. 47 u. m. , c. 44 u. m.
IV. Instrumente financiare derivate - aplicatii propuse 4. Un investitor anticipează creşterea cursului acţiunii AES, dar în acelaşi timp vrea să-şi limiteze pierderea. În acest scop, el adoptă o strategie formată astfel: o poziţie long pe o opţiune call cu preţul de exerciţiu 50 € şi prima 4 € şi o poziţie short pe o opţiune call cu acelaşi activ suport, preţ de exerciţiu 70 € şi prima 2 €. Să se determine: a) Rezultatul investitorului dacă la scadenţa contractelor cursul activului suport este 77 €; b) Rezultatul investitorului dacă la scadenţa contractelor cursul activului suport este 67 €; c) Cât ar trebui să fie cursul pentru ca rezultatul să fie nul.
IV. Instrumente financiare derivate - aplicatii propuse 5. Se consideră o strategie de tip butterfly formată din: P 1: o poziţie long call cu preţul de exercitare PE 1 şi prima c 1; P 2: două poziţii short call cu preţul de exercitare PE 2 şi prima c 2; P 3: o poziţie long call cu preţul de exercitare PE 3 şi prima c 3; Unde PE 1 < PE 2 < PE 3 şi c 1 > c 2 > c 3 cu c 1 = 4 u. m. , c 2 = 3 u. m. , c 3 = 2 u. m. În cazul în care la preţul de exercitiu PE 2 rezultatul din P 1 este egal cu rezultatul din P 2 şi la PE 3 rezultatul din P 2 este egal cu rezultatul din P 3, să se determine: a) b) c) PE 3 -PE 1; Câştigul maxim; Pierderea maximă.
IV. Instrumente financiare derivate - bibliografie • Anghelache G. , “Piaţa de capital: caracteristici, evoluţii, tranzacţii”, Ed. Economică, Bucureşti, 2004 • Anghelache G. şi colectiv, “Pieţe de capital şi tranzacţii bursiere” – aplicaţii şi studii de caz, Ed. Economică, Bucureşti, 2003 • Bodie, Z. , A. Kane, and A. J. Marcus (2007), Essentials of Investments, 6 th edition, Mc. Graw Hill International Edition
V. Indici bursieri • Cuprinsul unitatii de invatare 5: - Tipologia indicilor bursieri…………. . pag 90 Principii pentru construirea indicilor bursieri…………. …. . …………. . . …pag 91 Indici bursieri reprezentativi. . . ………………. pag 92 Aplicatii rezolvate……………. …. pag 93 Aplicatii propuse……………. . . …. pag 102 Bibliografie…………………. pag 103
V. Indici bursieri • Obiectivele unității de învățare V: - definirea indicilor bursieri - cunoaşterea modului de construire şi a utilităţii indicilor bursieri - Cunoaşterea indicilor reprezentativi la nivel Mondial şi la BVB
V. Indici bursieri • Produse sintetice care exprimă evoluţia valorilor mobiliare de pe o anumită piaţă • În funcţie de valorile mobiliare componente: - • - • - Pentru acţiuni Pentru obligaţiuni Pentru fonduri mutuale şi alte instrumente financiare În funcţie de modul de calcul: Indici din prima generaţie Indici din generaţia a doua În funcţie de gradul de cuprindere: Indici generali ai pieţei Indici sectoriali În funcţie de frecvenţa cu care sunt calculaţi: În timp real La sfârşitul zilei de tranzacţionare În funcţie de apartenenţa valorilor mobiliare: Valori mobiliare cotate pe o anumită piaţă Indici globali În funcţie de instituţia care îi calculează: Indici oficiali Indici calculaţi de instituţiile pieţei împreună cu diverse publicaţii Indici calculaţi de publicaţiile economico-financiare Indici calculaţi de intermediari sau firme de consultanţă
V. Indici bursieri • - Principii care trebuiesc respectate în construirea unui indice: Metodele de calcul trebuie să reflecte realitatea Metodele de calcul nu trebuie să fie foarte complexe Informaţiile trebuie furnizate de surse autorizate Trebuie să se asigure continuitatea şi comparabilitatea datelor Trebuie să satisfacă nevoia de informare Etapele de construire a indicilor bursieri: Alegerea eşantionului de valori mobiliare Importanţa valorilor mobiliare în cadrul indicelui - fără pondere - ponderare cu capitalizarea bursieră - pondere egală Alegerea datei de referinţă Calculul valorii indicelui: Pentru indicii din prima generaţie - Pentru indicii din a doua generaţie • • -
V. Indici bursieri • Indici importanţi la nivel mondial: - Dow Jones Standard&Poor’s 500 Frank Russel F-T 100 Nikkei Topix F-T Actuaries Solomon Russel Dow Jones Stoxx Dow Jones Euro Stoxx • Indicii BVB
V. Indici bursieri – aplicatii rezolvate - Calculul indicilor B şi C ce au următoarea evoluţie a bursieri 1. Un indice bursier are în componenţă acţiunile A, cursurilor: Acţiune A B C Preţ la moment t (u. m. ) 100 50 30 Preţ la moment t+1 (u. m. ) Cazul A Cazul B 110 100 50 50 30 33 Să se arate care este impactul modificărilor de preţ al acţiunilor asupra indicelui folosind ca metodă de calcul media aritmetică simplă. Rezolvare: Indicele se calculează folosind acelaşi divizor, respectiv D = 3 (divizorul este dat de numărul acţiunilor). Acţiune Moment t+1 A B C D I 100 50 30 180 3 60 - Cazul A 110 50 30 190 3 63, 3 + 5, 5% Cazul B 100 50 33 183 3 61 + 1, 7%
V. Indici bursieri – aplicatii rezolvate Calculul indicilor bursieri Concluzie. Din tabelul de mai sus se observă, modificarea indicelui este mai mare în cazul A, aceasta se justifică prin faptul că o creştere cu 10% la o acţiune un preţ mai mare (P 0 A = 100 u. m. ) va avea un impact mai mare asupra indicelui decât o creştere de 10% la o acţiune ce valorează mai puţin (P 0 B = 30).
V. Indici bursieri – aplicatii rezolvate Strategii cu indici bursieri • • 2. Un investitor anticipează o volatilitate redusă a cursului indicelui Dow Jones şi tranzacţionează un „straddle”, la preţ de exercitare de 7. 600 puncte, prima call fiind 120 puncte, iar prima put de 100 puncte. La scadenţă opţiunea put este abandonată de către cumpărătorul opţiunilor, iar vânzătorul obţine un rezultat de 35. 000 USD. Să se determine valoarea indicelui Dow Jones (MUSD = 500 USD) la scadenţă. Rezolvare: Volatitate redusă vânzare de straddle Pentru a putea construi strategia sintetizăm datele în tabelul de mai jos: Short straddle ST < PE ST > PE Short put ST – PE + p +p Short call +c PE - ST + c ST – PE + p + c PE - ST + c + p Rezultatul strategiei
V. Indici bursieri – aplicatii rezolvate Strategii cu indici bursieri I. Dacă ST < PE: ST – PE + p + c = 0 şi de aici rezultă primul prag de rentabilitate PR 1 = ST = PE – c – p = 7380 puncte II. Dacă ST > PE: PE - ST + c + p = 0 , de unde rezultă cel de-al doilea prag de rentabilitate PR 2 = ST = PE + c + p = 7820 puncte Grafic strategia se reprezintă astfel:
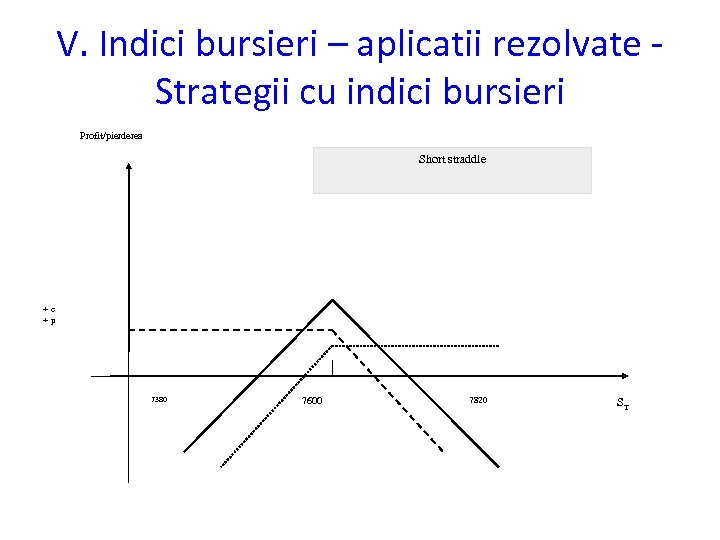V. Indici bursieri – aplicatii rezolvate Strategii cu indici bursieri Profit/pierderea Short straddle +c +p 7380 7600 7820 ST
V. Indici bursieri – aplicatii rezolvate Strategii cu indici bursieri La scadenţă opţiunea put este abandonată de cumpărator, prin urmare vânzatorul încasează prima, dar cumpărătorul de call exercită cu pierdere întrucât cursul indicelui se află între PR 1 şi PR 2. (7600 – ST +220) * 500 USD = 35000 USD, de unde rezultă că ST = 7750 puncte.
V. Indici bursieri – aplicatii rezolvate Strategii cu indici bursieri • • 3. Un trader previzionează pe piaţa americană o creştere a indicelui Dow Jones şi iniţiază o tranzacţie cu un contract de opţiune call de tip european pe indicele Dow Jones (MUSD = 500 USD), preţul de exercitare 10780 puncte, iar prima 250 puncte. De asemenea, investitorul previzionează o scădere a indicelui Nikkei (MJPY = 10000 JPY) şi tranzacţionează un contract put de tip american, cu preţul de exerciţiu 11980 puncte, iar prima 200 puncte. Pe parcursul duratei de viată a opţiunilor, indicii inregistrează următoarea evoluţie: cursul indicelui Dow Jones: t 1 = 10800; t 2 = 11030; t 3 = 11100; t 4 =11250 ; tn =11230. cursul indicelui Nikkei: t 1 = 11900; t 2 =11800; t 3 = 11750; t 4 = 11500; tn = 12500, tn – scadenta optiunii. Ţinând cont că traderul a obţinut câştigul maxim posibil, la scadenţa (tn), să se determine rezultatul final în tranzacţiile cu opţiuni pe indici bursieri (1 USD = 119, 25 JPY).
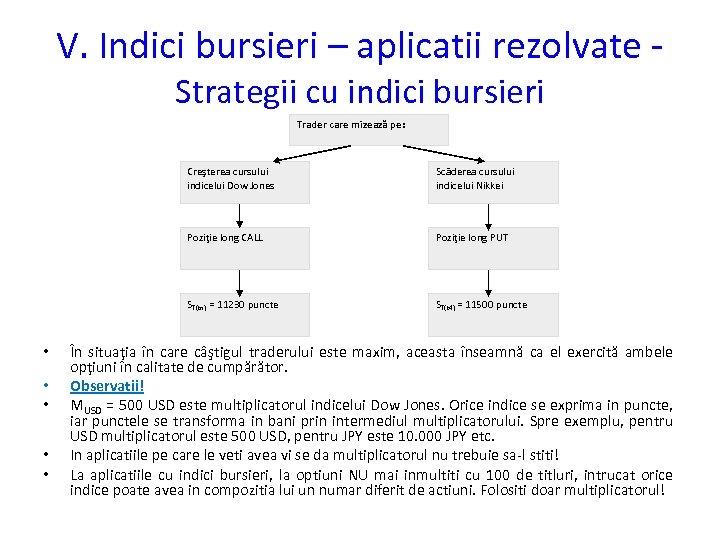V. Indici bursieri – aplicatii rezolvate Strategii cu indici bursieri Trader care mizează pe: Creşterea cursului indicelui Dow Jones Poziţie long CALL • • Poziţie long PUT ST(tn) = 11230 puncte • Scăderea cursului indicelui Nikkei ST(t 4) = 11500 puncte În situaţia în care câştigul traderului este maxim, aceasta înseamnă ca el exercită ambele opţiuni în calitate de cumpărător. Observatii! MUSD = 500 USD este multiplicatorul indicelui Dow Jones. Orice indice se exprima in puncte, iar punctele se transforma in bani prin intermediul multiplicatorului. Spre exemplu, pentru USD multiplicatorul este 500 USD, pentru JPY este 10. 000 JPY etc. In aplicatiile pe care le veti avea vi se da multiplicatorul nu trebuie sa-l stiti! La aplicatiile cu indici bursieri, la optiuni NU mai inmultiti cu 100 de titluri, intrucat orice indice poate avea in compozitia lui un numar diferit de actiuni. Folositi doar multiplicatorul!
V. Indici bursieri – aplicatii rezolvate Strategii cu indici bursieri Rezolvare: Rezultatul traderului în opţiunea CALL europeană pe indicele Dow Jones va fi: R final long call = (ST – PE - c) * MUSD = (11230 – 10780 - 250) * 500 USD = 100. 000 USD Rezultatul traderului în opţiunea PUT americană pe indicele Nikkei va fi: R final long put = (PE – ST - p) * MJPY = (11980 – 11500 - 200) * 500 USD = 2. 800. 000 JPY R final long put USD = Prin urmare, rezultatul total al traderului este 123. 480 USD.
V. Indici bursieri – aplicatii propuse 1. Un investitor anticipează o scădere a valorii indicelui Dow Jones şi tranzacţionează 10 de contracte futures pe indicele Dow Jones, cursul indicelui este 10. 300 puncte. La scadenţă acesta lichidează contractele futures la 98, 6% din valoarea la care a iniţiat pozitia. Din câştigul obţinut investitorul cumpără 100 obligaţiuni S, emise in urmă cu 3 ani. Preţul de achiziţie al unei obligaţiuni reprezintă 90, 125% din valoarea nominală, cuponul este 800, maturitatea este de 8 ani, iar obligaţiunile sunt răscumpărabile la scadenţă la paritate. Să se determine randamentul la maturitate al obligaţiunii S. 2. Un investitor ce anticipează o creştere a valorii indicelui S&P 500 tranzacţionează 20 de contracte futures pe acest indice la un curs la termen de 1247, 5 puncte (multiplicatorul acestei pieţe este de 500 $). Pentru a se acoperi împotriva unei evoluţii nefavorabile a indicelui S&P 500, investitorul cumpără 20 de opţiuni pe indicele S&P 500 ce au o prima de 12, 5 puncte. Dacă la un curs al indicelui la scadenţă de 1235, rezultatul investitorului ar fi 0, atunci preţul de exerciţiu cat va fi?
V. Indici bursieri – bibliografie • Anghelache G. , “Piaţa de capital: caracteristici, evoluţii, tranzacţii”, Ed. Economică, Bucureşti, 2004 • Anghelache G. şi colectiv, “Pieţe de capital şi tranzacţii bursiere” – aplicaţii şi studii de caz, Ed. Economică, Bucureşti, 2003 • Bodie, Z. , A. Kane, and A. J. Marcus (2007), Essentials of Investments, 6 th edition, Mc. Graw Hill International Edition
• Notă: Acest material a fost realizat împreună cu Carmen Obreja (partea teoretică) şi Alina Sima (Grigore) (partea aplicativă)