Physics Temperature and Heat Teacher Luiz Izola

Physics Temperature and Heat Teacher: Luiz Izola

Chapter Preview 1. Zeroth Law of Thermodynamics 2. Temperature Scales 3. Thermal Expansion 4. Heat and Mechanical Work 5. Specific Heats 6. Conduction, Convection, and Radiation

Introduction Ø Up to now, we studied mass, length, and time. Now, we will: ØIntroduce a fourth physical quantity: temperature ØLearn about Heat: A particular type of energy transfer ØDiscuss the connection between changes in temperature and changes in other physical quantities such as length, pressure, and volume. ØConsider mechanisms by which thermal energy is exchanged.

Temperature and Heat Flow Ø Heat is the energy transferred between objects because of a difference in temperature. Ø When heat flows from object A to object B, A loses energy and B gains it. ØWhen heat flows between the objetcs, they are in thermal contact. ØWhen the transfer of heat stops, the objects reached thermal equilibrium. ØThermodynamics studies the physical processes involving the transfer of heat.

Zeroth Law of Thermodynamics Ø Basic idea of Thermodynamics: Thermal Equilibrium is determined by a single physical quantity, Temperature. “If object A is in thermal equilibrium with B, and C is in equilibrium with B, then, A is in equilibrium with C. ”

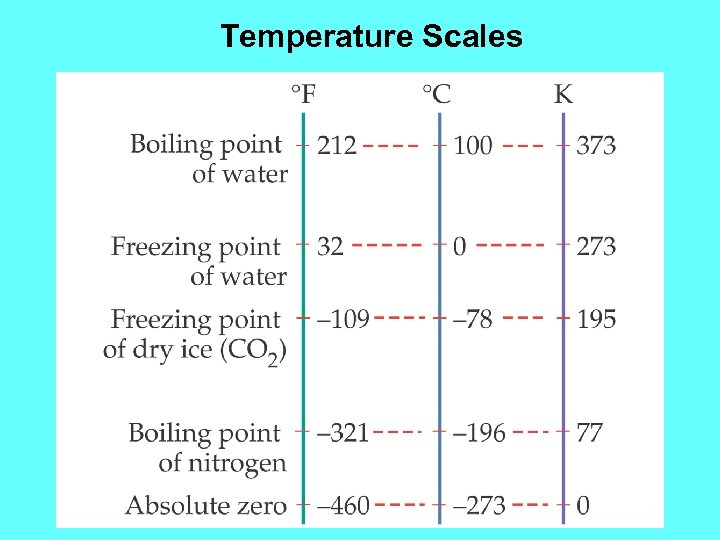
Celsius Temperature Scale Ø There are three main temperature scales: Celsius, Kelvin, and Fahrenheit. Ø Celsius defines 00 C as freezing water and 1000 C as boiling water temperature. Ø In Celsius scale, there is no limit for how high a temperature can go. There is a lower limit: -2730 C Celsius Notation: Temperature Change: 1000 C 100 C 0

Fahrenheit Temperature Scale Ø Fahrenheit defines 320 F as freezing water and 2120 F as boiling water temperature. Fahrenheit Notation: Temperature Change: 1000 F 100 F 0 Conversion of Celsius to Fahrenheit Tf = 9/5 Tc + 32 Conversion of Celsius to Fahrenheit Tc = 5/9(Tf - 32)

Example - 1 Ø Find the corresponding temperatures for the following: § 200 C to 0 F § 950 F to 0 C § 600 C to 0 F § 2120 F to 0 C § 1000 C to 0 F § 320 F to 0 C

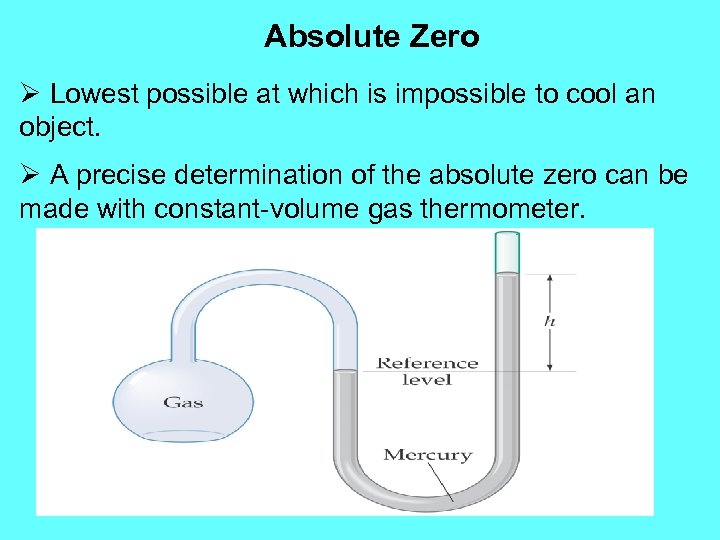Absolute Zero Ø Lowest possible at which is impossible to cool an object. Ø A precise determination of the absolute zero can be made with constant-volume gas thermometer.

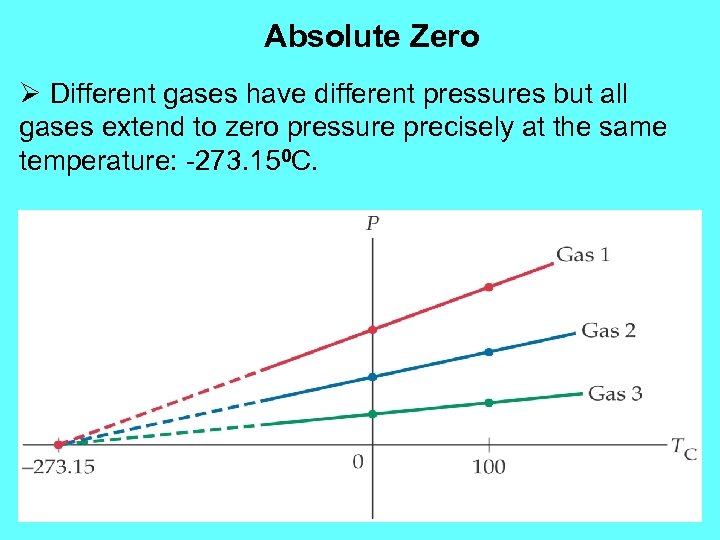Absolute Zero Ø Different gases have different pressures but all gases extend to zero pressure precisely at the same temperature: -273. 150 C.

Example - 2 Ø The gas in a constant-volume thermometer has a pressure of 80 k. Pa at 0. 000 C. Assuming the ideal behavior of the picture below, what is the pressure at 1050 C? Find the temperature of the gas at 70. 0 k. Pa of pressure.

Kelvin Scale Ø It is based on existence of the absolute zero. Ø The zero on the Kelvin scale (0 K) is the absolute zero. Ø Kelvin scale has the same degree size as the Celsius scale. Therefore the -273. 150 C is equal to 0 K. Conversion between 0 C and K Tk = Tc + 273. 15 Ø Change F to K in example – 2 and calculate the new temperatures.

Temperature Scales

Thermal Expansion Ø Most substances expand when heated. For example, fever is measured by the expansion of mercury in a tube. Ø We will discuss three types of thermal expansion: linear, area, and volume. Linear Expansion (ΔL) ØLength changes are proportional to the temperature change. ΔL = (constant)ΔT

Thermal Expansion Ø Most substances expand when heated. For example, fever is measured by the expansion of mercury in a tube. Ø We will discuss three types of thermal expansion: linear, area, and volume. Linear Expansion (ΔL) ØLength changes are proportional to the temperature change. ΔL = (constant)ΔT

Thermal Expansion Ø When rod 1 is heated by an amount ΔT, its length increases by ΔL. If rod 2, which is twice as long as rod 1 and made of the same material, is heated by the same amount, does its length increase by (a) ΔL, (b) 2ΔL, or (c) ΔL/2? The constant that determines the proportionality of expansion, called coefficient of linear expansion (α) is defined as follows: ΔL = αL 0 ΔT Ex: An iron tower is 301 meters high at 220 C. How much does its height decrease when the temperature goes to 00 C?

Thermal Expansion Ø Two different metals have different coefficients of linear expansions. Area Expansion (ΔA) Using the square as the area to generate the final formula we have: A’ = (L + ΔL)2 = L 2 + 2αL 2ΔT + α 2 L 2ΔT 2 If αΔT is much less than one, then α 2ΔT 2 is even smaller. Then, A’ = L 2 + 2αL 2ΔT = A + 2αL 2ΔT. ΔA = A’ – A = 2αAΔT

Thermal Expansion Ø A washer has a hole in the middle. As the washer is heated, does the hole (a) expand, (b) shrink, or (c) stay the same? Volume Expansion (ΔV) Using the cube as the area with side L, prove that ΔV is equals: ΔV = V’ – V = 3αVΔT Coefficient of Volume Expansion (β) are given for different liquids: ΔV = βVΔT

Coefficients of Thermal Expansion Substance Coefficient of linear Expansion, a (K– 1) Lead 29 x 10– 6 Substance Coefficient of volume expansion, b (K– 1) Ether 1. 51 x 10– 3 Aluminum 24 x 10– 6 1. 18 x 10– 3 Brass 19 x 10– 6 Carbon tetrachloride Alcohol 1. 01 x 10– 3 Gasoline 0. 95 x 10– 3 Olive oil 0. 68 x 10– 3 17 x 10– 6 Copper 12 x 10– 6 Window glass 11 x 10– 6 Water 0. 21 x 10– 3 Pyrex glass 3. 3 x 10– 6 Mercury 0. 18 x 10– 3 Quartz 0. 50 x 10– 6 Iron (Steel) Concrete

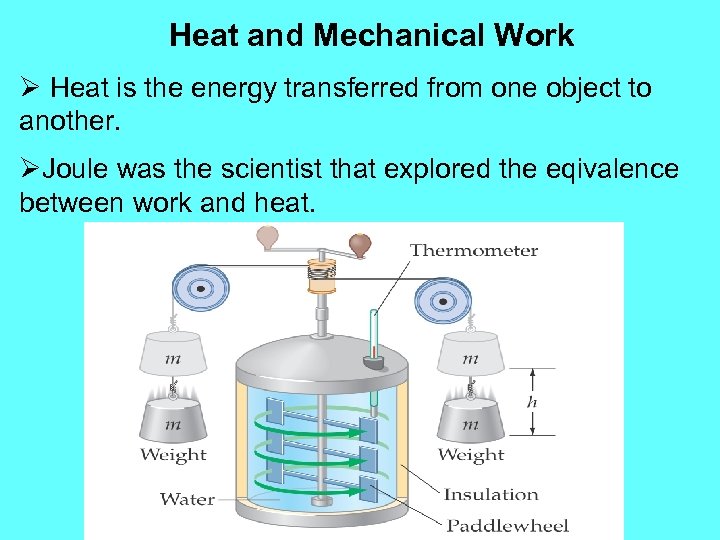Heat and Mechanical Work Ø Heat is the energy transferred from one object to another. ØJoule was the scientist that explored the eqivalence between work and heat.

Heat and Mechanical Work Ø In the previous picture, a total mass 2 m falls through a certain distance h. This generates loss of work equals to 2 mgh. The masses falling generated paddles´ movement on which created a ΔT increase of water temperature. Ø Joule´s experiments established the precise amount of mechanical work that has the same effect as a given transfer of heat. Ø Before Joule, heat was measure in calorie (cal). One kilocalorie (kcal) was the amount of heat needed to raise the temperature of 1 kg of water from 14. 50 C to 15. 50 C.

Heat and Mechanical Work Ø Joule was able to show that 1 kcal = 4186 J. Mechanical equivalent of Heat 1 cal = 4. 186 J Other units are C (Calorie nutrition) = 1 kcal Btu (British Thermal Unit) = 0. 252 kcal = 1055 J Ø Finally, Q denotes heat (energy transferred due to 2 different temperatures)

Heat and Mechanical Work Ø A 74 -kg person drinks a thick 305 -C shake. How many stairs must this person climb to work off the shake? Let the height of the stair be 20. 0 cm.

Specific Heats – Heat Capacity Ø It takes 4186 J of heat to raise the temperature of 1 kg of water by 10 C. Ø The heat required for an increase in temperature is given by the heat capacity of the substance. Heat Capacity (C) C = Q / ΔT Ø The unit for heat capacity is J/K = J/C 0 An object can gain/release heat when in thermal contact with other objects. Objects cannot be taught of as holding a certain amount of heat.

Specific Heats – Heat Capacity Ø Heat capacity is always positive. Ø Q is positive if ΔT is positive Ø Q is negative if ΔT is negative Ex: The heat capacity of 1. 00 kg of water is 4186 J/K. What is the temperature change in the water if (a) 505 J of heat is added to the system, or (b) 1010 J of heat is removed? Ex: Suppose 63 J of heat is added to a 128 -g piece of aluminum at 250 C. What is the final temperature of the aluminum piece?

Specific Heats – Heat Capacity Ø Heat capacity varies not only with the type of material but also with the amount of substance. Ø Specific Heat (c) – It is a type of heat that depends only on the type of substance, not the amount. Specific Heat (c) c = Q / m ΔT (J / (kg. C 0) Ø Water specific heat is the largest of any common material. Ø Water can give off or take in large quantities of heat with little change in temperature

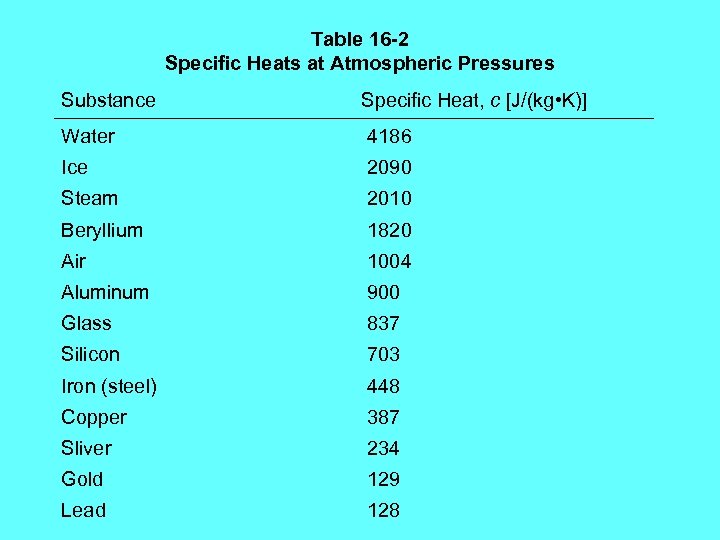Table 16 -2 Specific Heats at Atmospheric Pressures Substance Specific Heat, c [J/(kg • K)] Water 4186 Ice 2090 Steam 2010 Beryllium 1820 Air 1004 Aluminum 900 Glass 837 Silicon 703 Iron (steel) 448 Copper 387 Sliver 234 Gold 129 Lead 128

Calorimetry Suppose a block of mass mb, specific heat cb, and initial temperature Tb is dropped into a calorimeter containing water with mass mw, specific heat cw, and initial temperature Tw. Assume (a) Final temperature of block and water are the same and (b) the total energy of the system is conserved. Qb + Qw = 0 Applying the specific heat formula, we have: mb cb(T - Tb) + mw cw(T - Tw) = 0 Solving for T, we have: T = (mb cb. Tb + mw cw. Tw) / (mb cb + mw cw)

Calorimetry Ex: Suppose 550 -g of water at 320 C are poured into a 210 -g aluminum can with an initial temperature of 150 C. Find the final temperature of the system, assuming no heat is exchanged with the surroundings. Ex: A 0. 50 -kg block of metal with an initial temperature of 300 C is dropped into a container holding 1. 12 -kg of water at 200 C. If the final temperature of the system is 20. 40 C, what is the specific heat of the metal? Assume the container can be ignored, and that no heat is exchanged with the surroundings.

Conduction, Convection, and Radiation Conduction The flow of heat directly through a physical material. Ø Conduction depends on the material being used. Ø Poor conductors are considered Insulators. Experiments show that the amount of heat Q that flows through a rod: Increases in proportion to the rod´s area (A). Increases in proportion to ΔT = T 2 – T 1 Increases with time t. Decreases with the length of the rod, L.

Conduction, Convection, and Radiation Conduction The flow of heat directly through a physical material. Ø Conduction depends on the material being used. Ø Poor conductors are considered Insulators. Experiments show that the amount of heat Q that flows through a rod: Increases in proportion to the rod´s area (A). Increases in proportion to ΔT = T 2 – T 1 Increases with time t. Decreases with the length of the rod, L.

Conduction, Convection, and Radiation Heat (Q) flow by Conduction Q = k. A(ΔT / L)t Thermal Conductivities Substance Silver Copper Gold Aluminum Steel, low carbon Lead Stainless steel Ice Concrete Glass Water Asbestos Wood Wool Air Thermal Conductivity, k [W/(m • K)] 417 395 291 217 66. 9 34. 3 16. 3 1. 6 1. 3 0. 84 0. 60 0. 25 0. 10 0. 040 0. 0234

Conduction, Convection, and Radiation Ex: One of the windows in a house has a squared shape with 1. 00 -m side. The glass of the windows is 0. 50 -cm thick. How much heat is lost through the window in one day if the temperature in the house is 21. 00 C and outside 0. 00 C? Ex: Two meta rods are used to conduct heat from a region 1000 C to a 00 C region. The rods can be arranged as below. Is the heat conducted in the parallel arrangement greater, same, or less that the one in series?

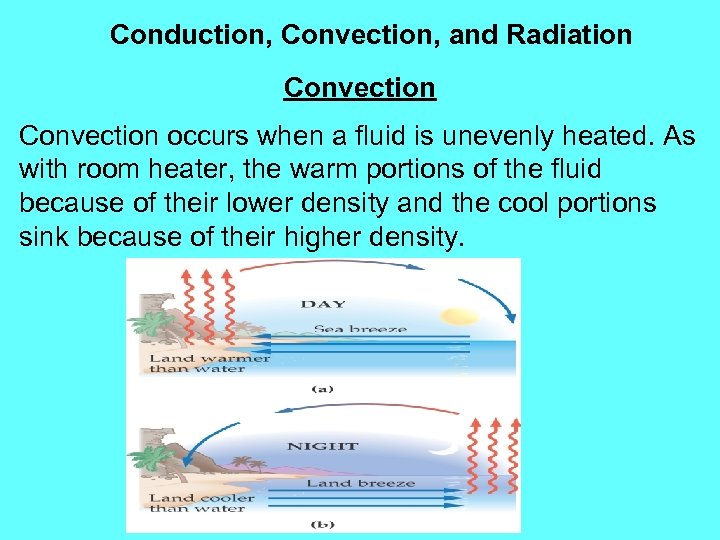Conduction, Convection, and Radiation Convection occurs when a fluid is unevenly heated. As with room heater, the warm portions of the fluid because of their lower density and the cool portions sink because of their higher density.