Скачать презентацию Physics Projects and the Prime Minister s visit
L 17 Diffraction.ppt
- Количество слайдов: 19
Physics Projects and the Prime Minister’s visit • In connection with the Kazakhstan Prime minister’s visit to the University, the leaders of the following Physics project teams should meet Steve in the Physics office between 12. 00 pm and 2. 00 pm today, 5 th December 2011.
1) DA VINCI TUESDAY 2 2) DA VINCI FRIDAY 5 3) NEWTON TUESDAY 9 4) NEWTON THURSDAY 2 5) TESLA TUESDAY 2 6) TESLA THURSDAY 2
Diffraction At the end of this lecture you should • Understand what is meant by diffraction • Understand the nature of single slit diffraction and have a qualitative idea of how the diffraction pattern depends upon the slit width • Know the formula for single slit diffraction • Know how to use the formula for a diffraction grating
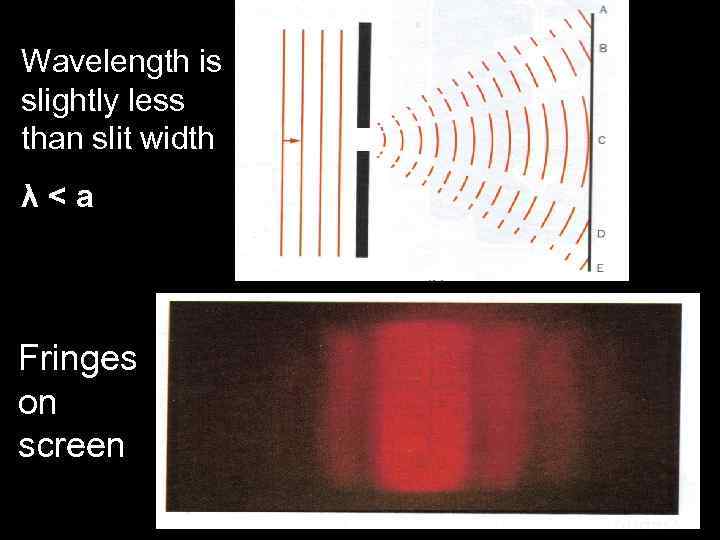
Diffraction occurs when a wave is incident onto an obstacle or an aperture. The wave “bends” around the obstacle or “spreads out” after passing through an aperture. Examples: Long radio waves that can bend around hills Light waves after passing through a very small opening.
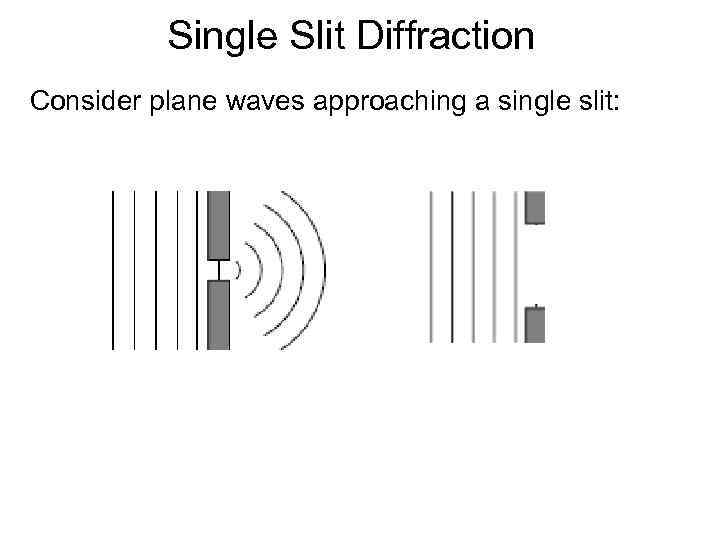Single Slit Diffraction Consider plane waves approaching a single slit: A B
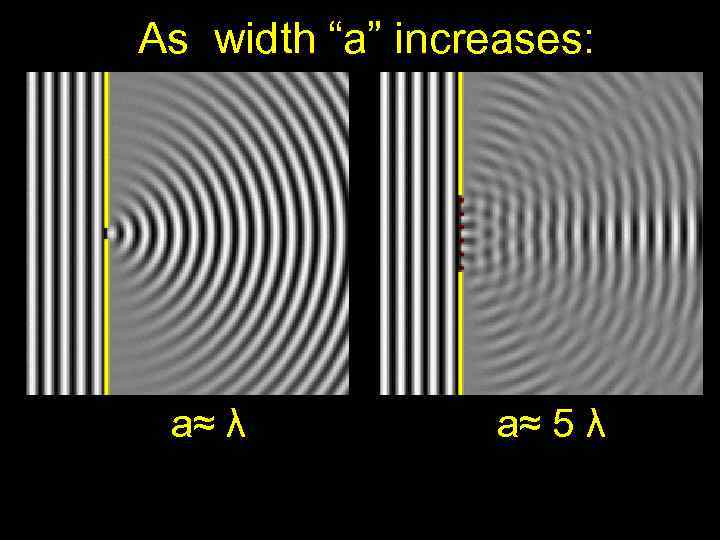As width “a” increases: a≈ λ a≈ 5 λ
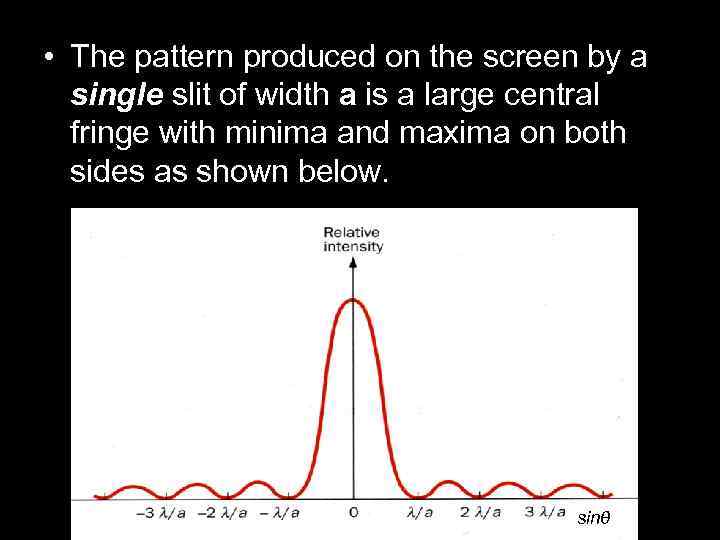• The pattern produced on the screen by a single slit of width a is a large central fringe with minima and maxima on both sides as shown below. sinθ
Condition for single slit diffraction The angles on either side of the central maximum at which the minima of the diffraction pattern occur are given by: m=1, 2, 3…
Huygens’s principle Every point of a wavefront may be considered the source of secondary wavelets that spread out in all directions with a speed equal to the speed of propagation of the waves.
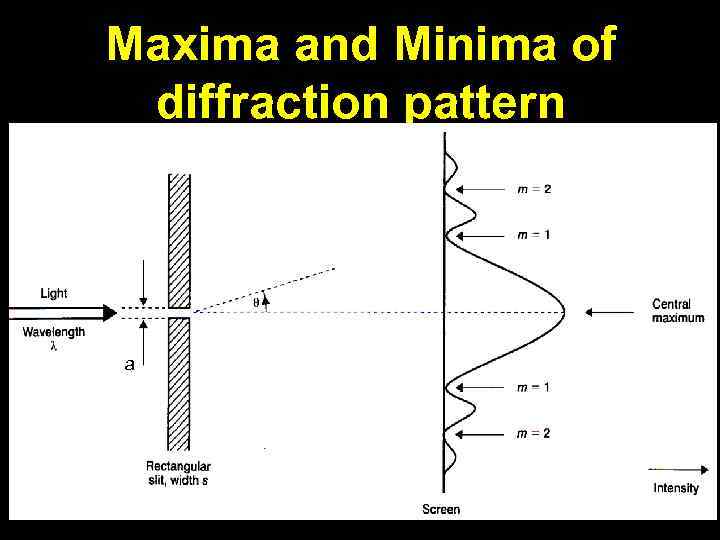Maxima and Minima of diffraction pattern a
Example 1 • Laser light of wavelength 650 nm is incident on a single slit of width 0. 130 mm. The diffraction pattern is observed on a screen placed 3. 00 m from the slit. • Calculate the width of the central maximum. • How many minima can be observed on either side of the central maximum?
Example 2 Water waves of wavelength λ are incident on a slit. The slit is gradually narrowed until, at 2 cm, only one large central maximum can be observed. Find λ.
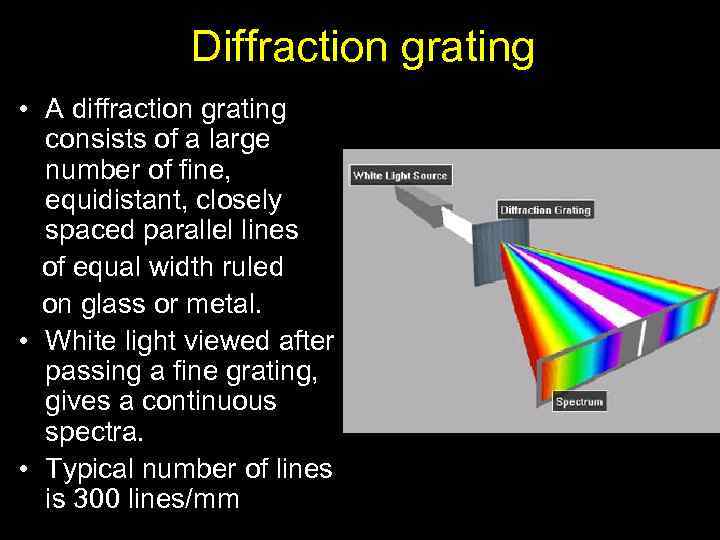Diffraction grating • A diffraction grating consists of a large number of fine, equidistant, closely spaced parallel lines of equal width ruled on glass or metal. • White light viewed after passing a fine grating, gives a continuous spectra. • Typical number of lines is 300 lines/mm
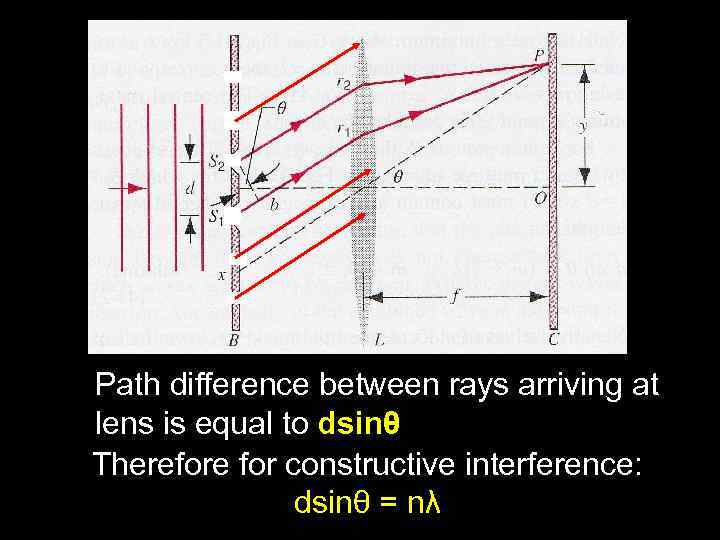Path difference between rays arriving at lens is equal to dsinθ Therefore for constructive interference: dsinθ = nλ
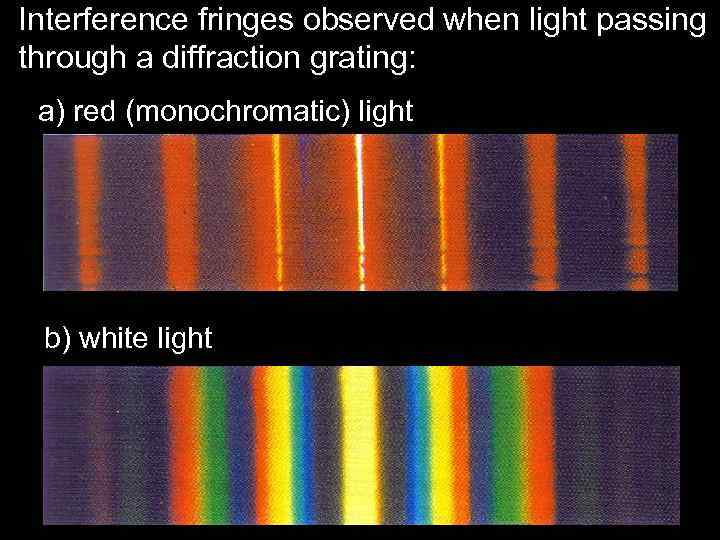Interference fringes observed when light passing through a diffraction grating: a) red (monochromatic) light b) white light
Monochromatic light: alternating bright and dark bands. White light: multi-coloured bands. The maxima and minima for each wavelength in the white light occur at different angles. We can use a diffraction grating to produce monochromatic light. Note: the principles of a diffraction grating are used throughout physics, engineering and chemistry to analyse materials. By studying the wavelengths emitted and absorbed by materials we can determine important details about the atomic/molecular structure.
Spectra of different orders nλ = dsinθn Note: the same formula as derived for Young’s double-slit experiment holds. (Angles can be much larger than for Young’s slits). The central bright maximum corresponds to n=0. At n=1, 2, etc, we observe first -order, second-order spectra, etc.
Example 3 Calculate the angular separation of the red and violet rays in the firstorder spectrum when a parallel beam of white light is incident normally on a diffraction grating of 5000 lines/cm. Take λred = 700 nm and λviolet = 400 nm.