Physics of Semiconductor Devices Lecture 5. The





























lecture_5.pptx
- Размер: 1.1 Мб
- Автор:
- Количество слайдов: 33
Описание презентации Physics of Semiconductor Devices Lecture 5. The по слайдам
 Physics of Semiconductor Devices Lecture 5. The Five Basic Equations. A. V. Sogoyan
Physics of Semiconductor Devices Lecture 5. The Five Basic Equations. A. V. Sogoyan
 Contents: • Doped semiconductor in thermal equilibrium • NE conditions • G&R rates outside thermal equilibrium
Contents: • Doped semiconductor in thermal equilibrium • NE conditions • G&R rates outside thermal equilibrium
 Basic Equations System of non-linear, coupled partial differential equations.
Basic Equations System of non-linear, coupled partial differential equations.
 Basic Equations Doped semiconductor in thermal equilibrium It is possible to have an electric field in a semiconductor in thermal equilibrium non-uniform doping distribution⇒ Gauss’ Law: electrical charge produces an electric field:
Basic Equations Doped semiconductor in thermal equilibrium It is possible to have an electric field in a semiconductor in thermal equilibrium non-uniform doping distribution⇒ Gauss’ Law: electrical charge produces an electric field:
 Doped semiconductor in thermal equilibrium In semiconductors: • Uniformly-doped semiconductor in TE: far away from any surface charge neutrality: ⇒ since no field applied from the outside ⇒
Doped semiconductor in thermal equilibrium In semiconductors: • Uniformly-doped semiconductor in TE: far away from any surface charge neutrality: ⇒ since no field applied from the outside ⇒
 Doped semiconductor in thermal equilibrium Non-uniformly doped semiconductor in TE (n-type):
Doped semiconductor in thermal equilibrium Non-uniformly doped semiconductor in TE (n-type):
 Doped semiconductor in thermal equilibrium In TE, diffusion = drif there must be a ⇒ connection between electrostatics and carrier concentrations. In TE J e =0: Then, relationship between E o and equilibrium carrier concentration: Express in terms of φ:
Doped semiconductor in thermal equilibrium In TE, diffusion = drif there must be a ⇒ connection between electrostatics and carrier concentrations. In TE J e =0: Then, relationship between E o and equilibrium carrier concentration: Express in terms of φ:
 Doped semiconductor in thermal equilibrium Relationship between the ratio of equilibrium carrier concentration and difference of electrostatic potential at two different points. At 300 K: factor of 10 in ”⇒ 60 m. V/decade rule” If φ(ref)= 0 where n o = n i : Similarly:
Doped semiconductor in thermal equilibrium Relationship between the ratio of equilibrium carrier concentration and difference of electrostatic potential at two different points. At 300 K: factor of 10 in ”⇒ 60 m. V/decade rule” If φ(ref)= 0 where n o = n i : Similarly:
 Doped semiconductor in thermal equilibrium Equilibrium carrier concentration: general solution in the presence of doping gradient (n-type) Relationship between E o and n o in thermal equilibrium (from J e =0): One equation, one unknown. Given N D (x), can solve for n o (x) (but in general, require numerical solution).
Doped semiconductor in thermal equilibrium Equilibrium carrier concentration: general solution in the presence of doping gradient (n-type) Relationship between E o and n o in thermal equilibrium (from J e =0): One equation, one unknown. Given N D (x), can solve for n o (x) (but in general, require numerical solution).
 Doped semiconductor in thermal equilibrium If ND(x) changes slowly with x n⇒ o (x) will also change slowly, then: The majority carrier concentration closely tracks the doping level. When does this simple result apply? or Define Debye length:
Doped semiconductor in thermal equilibrium If ND(x) changes slowly with x n⇒ o (x) will also change slowly, then: The majority carrier concentration closely tracks the doping level. When does this simple result apply? or Define Debye length:
 Doped semiconductor in thermal equilibrium Rewrite condition: is change in electrostatic potential over a Debye length For a non-uniformly doped profile to be quasi-neutral in TE, the change in the electrostatic potential over a Debye length must be smaller than thermal voltage. L D is a characteristic length for electrostatic problems in semiconductors.
Doped semiconductor in thermal equilibrium Rewrite condition: is change in electrostatic potential over a Debye length For a non-uniformly doped profile to be quasi-neutral in TE, the change in the electrostatic potential over a Debye length must be smaller than thermal voltage. L D is a characteristic length for electrostatic problems in semiconductors.
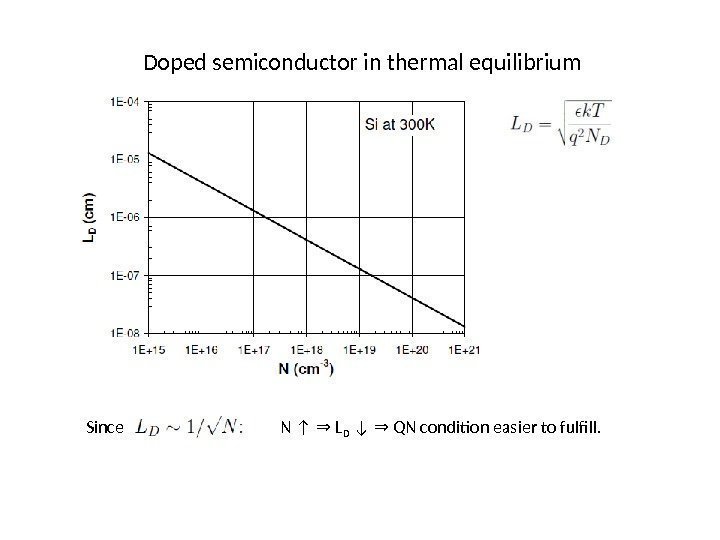
 Doped semiconductor in thermal equilibrium Since N ↑ L⇒ D ↓ QN condition easier to fulfill. ⇒
Doped semiconductor in thermal equilibrium Since N ↑ L⇒ D ↓ QN condition easier to fulfill. ⇒
 Basic Equations
Basic Equations
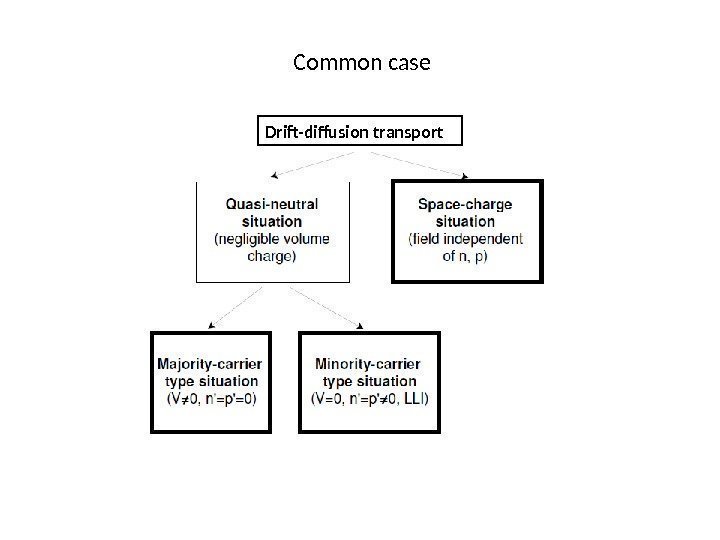
 Basic Equations Equation set difficult because of coupling through Gauss’ law. Two broad classes of important situations break Gauss’law coupling: 1. Carrier concentrations are high: quasi-neutral situation: 2. Carrier concentrations are very low: space-charge and high-resistivity situations:
Basic Equations Equation set difficult because of coupling through Gauss’ law. Two broad classes of important situations break Gauss’law coupling: 1. Carrier concentrations are high: quasi-neutral situation: 2. Carrier concentrations are very low: space-charge and high-resistivity situations:
 Common case Drift-diffusion transport
Common case Drift-diffusion transport
 Basic Equations: Quasi-neutral approximation At every location, the net volume charge that arises from a discrepancy of the concentration of positive and negative species is negligible in the scale of the charge density that is present. QN approximation eliminates Gauss’ law from the set: • Quasi-neutrality in equilibrium: • Additionally, quasi-neutrality outside equilibrium: • QN approximation good if n, p high carriers move to erase ⇒ ρ. • QN holds if length scale of problem >> Debye length L
Basic Equations: Quasi-neutral approximation At every location, the net volume charge that arises from a discrepancy of the concentration of positive and negative species is negligible in the scale of the charge density that is present. QN approximation eliminates Gauss’ law from the set: • Quasi-neutrality in equilibrium: • Additionally, quasi-neutrality outside equilibrium: • QN approximation good if n, p high carriers move to erase ⇒ ρ. • QN holds if length scale of problem >> Debye length L
 Basic Equations: Quasi-neutral approximation Consequence of quasi-neutrality Subtract one continuity equation from the other: continuity equation for net volume charge: if J t changes with position, ρ changes with time. In Static case: In Dynamic case, in times scale of interest
Basic Equations: Quasi-neutral approximation Consequence of quasi-neutrality Subtract one continuity equation from the other: continuity equation for net volume charge: if J t changes with position, ρ changes with time. In Static case: In Dynamic case, in times scale of interest
 Basic Equations: Quasi-neutral approximation Simplified set of basic equations for 1 D quasi-neutral situations
Basic Equations: Quasi-neutral approximation Simplified set of basic equations for 1 D quasi-neutral situations
 Basic Equations: Quasi-neutral approximation Majority-carrier type situations Voltage applied to extrinsic quasi-neutral semiconductor without upsetting the equilibrium carrier concentrations.
Basic Equations: Quasi-neutral approximation Majority-carrier type situations Voltage applied to extrinsic quasi-neutral semiconductor without upsetting the equilibrium carrier concentrations.
 Basic Equations: Quasi-neutral approximation Majority-carrier type situations Characteristics of majority carrier-type situations: • electric field imposed from outside • electrons and holes drif • electron and hole concentrations unperturbed from TE Simplifications: • neglect contribution of minority carriers • neglect time derivatives of carrier concentrations ⇒ problem becomes completely quasi-static
Basic Equations: Quasi-neutral approximation Majority-carrier type situations Characteristics of majority carrier-type situations: • electric field imposed from outside • electrons and holes drif • electron and hole concentrations unperturbed from TE Simplifications: • neglect contribution of minority carriers • neglect time derivatives of carrier concentrations ⇒ problem becomes completely quasi-static
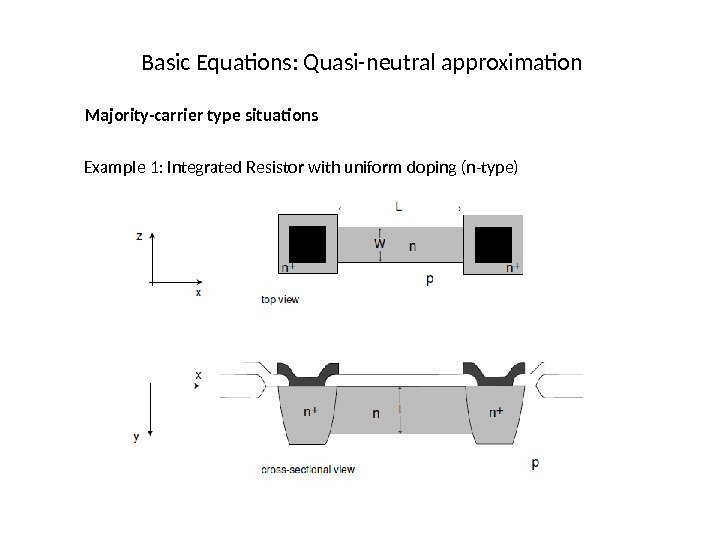
 Basic Equations: Quasi-neutral approximation Majority-carrier type situations Example 1: Integrated Resistor with uniform doping (n-type)
Basic Equations: Quasi-neutral approximation Majority-carrier type situations Example 1: Integrated Resistor with uniform doping (n-type)
 Basic Equations: Quasi-neutral approximation Majority-carrier type situations Example 1: Integrated Resistor with uniform doping (n-type) Uniform doping E⇒ o = 0, then: If E not too high,
Basic Equations: Quasi-neutral approximation Majority-carrier type situations Example 1: Integrated Resistor with uniform doping (n-type) Uniform doping E⇒ o = 0, then: If E not too high,
 Basic Equations: Quasi-neutral approximation Minority-carrier type situations Situations characterized by: • excess carriers over TE • no external electric field applied (but small internal field generated by carrier injection: E= E o + E’) Example: electron transport through base of npn BJT. Two approximations: 2. Low-level injection for n-type: ⇒ 1. E small: • negligible minority carrier drif due to E 0 (but can’t say the same about majority carriers)
Basic Equations: Quasi-neutral approximation Minority-carrier type situations Situations characterized by: • excess carriers over TE • no external electric field applied (but small internal field generated by carrier injection: E= E o + E’) Example: electron transport through base of npn BJT. Two approximations: 2. Low-level injection for n-type: ⇒ 1. E small: • negligible minority carrier drif due to E 0 (but can’t say the same about majority carriers)
 Basic Equations: Quasi-neutral approximation Minority-carrier type situations • Majority-carrier current equation:
Basic Equations: Quasi-neutral approximation Minority-carrier type situations • Majority-carrier current equation:
 Basic Equations: Quasi-neutral approximation Minority-carrier type situations • Minority-carrier current equation: • Minority-carrier continuity equation:
Basic Equations: Quasi-neutral approximation Minority-carrier type situations • Minority-carrier current equation: • Minority-carrier continuity equation:
 Basic Equations: Quasi-neutral approximation Minority-carrier type situations Now plug in J h from above: One differential equation with one unknown: p’.
Basic Equations: Quasi-neutral approximation Minority-carrier type situations Now plug in J h from above: One differential equation with one unknown: p’.
 Basic Equations: Quasi-neutral approximation Minority-carrier type situations
Basic Equations: Quasi-neutral approximation Minority-carrier type situations
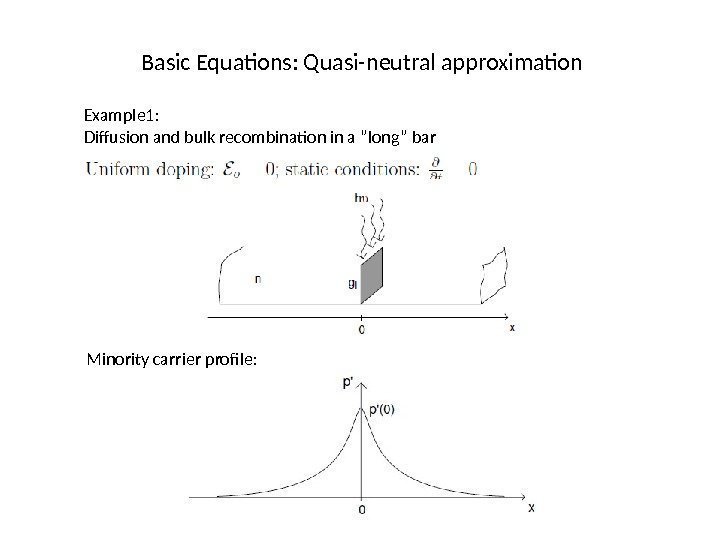
 Basic Equations: Quasi-neutral approximation Example 1: Diffusion and bulk recombination in a ”long” bar Minority carrier profile:
Basic Equations: Quasi-neutral approximation Example 1: Diffusion and bulk recombination in a ”long” bar Minority carrier profile:
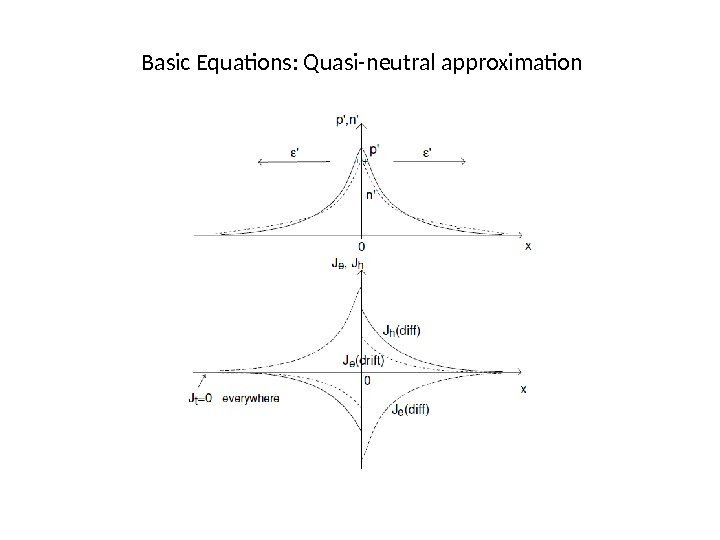
 Basic Equations: Quasi-neutral approximation Majority carrier profile? N’= p’ exactly? Far away J t =0 J⇒ t =0 everywhere.
Basic Equations: Quasi-neutral approximation Majority carrier profile? N’= p’ exactly? Far away J t =0 J⇒ t =0 everywhere.
 Basic Equations: Quasi-neutral approximation
Basic Equations: Quasi-neutral approximation
 Basic Equations: Quasi-neutral approximation Step 1. Minority carrier flow problem(for x> 0): B. C. at x =0: Step 2. Hole current: Assuming
Basic Equations: Quasi-neutral approximation Step 1. Minority carrier flow problem(for x> 0): B. C. at x =0: Step 2. Hole current: Assuming
 Basic Equations: Quasi-neutral approximation Step 3. Electron current:
Basic Equations: Quasi-neutral approximation Step 3. Electron current:
 Conclusions • Minority-carrier type situations dominated by behavior of minority carriers: diffusion, recombination and drif. • Minority-carrier type situations called that way because: -length and time scales of problem dominated by minority carrier behavior (diffusion, recombination, and drif). -role of majority carriers is to preserve quasi-neutrality and total current continuity
Conclusions • Minority-carrier type situations dominated by behavior of minority carriers: diffusion, recombination and drif. • Minority-carrier type situations called that way because: -length and time scales of problem dominated by minority carrier behavior (diffusion, recombination, and drif). -role of majority carriers is to preserve quasi-neutrality and total current continuity

