Physics of Semiconductor Devices Lecture 5 The Five

Physics of Semiconductor Devices Lecture 5. The Five Basic Equations. A. V. Sogoyan

Contents: • Doped semiconductor in thermal equilibrium • NE conditions • G&R rates outside thermal equilibrium

Basic Equations System of non-linear, coupled partial differential equations.

Basic Equations Doped semiconductor in thermal equilibrium It is possible to have an electric field in a semiconductor in thermal equilibrium ⇒ non-uniform doping distribution Gauss’ Law: electrical charge produces an electric field:

Doped semiconductor in thermal equilibrium In semiconductors: • Uniformly-doped semiconductor in TE: far away from any surface ⇒charge neutrality: since no field applied from the outside ⇒

Doped semiconductor in thermal equilibrium Non-uniformly doped semiconductor in TE (n-type):

Doped semiconductor in thermal equilibrium In TE, diffusion = drift ⇒ there must be a connection between electrostatics and carrier concentrations. In TE Je=0: Then, relationship between Eo and equilibrium carrier concentration: Express in terms of φ:

Doped semiconductor in thermal equilibrium Relationship between the ratio of equilibrium carrier concentration and difference of electrostatic potential at two different points. At 300 K: factor of 10 in ⇒ ” 60 m. V/decade rule” If φ(ref)= 0 where no = ni: Similarly:

Doped semiconductor in thermal equilibrium Equilibrium carrier concentration: general solution in the presence of doping gradient (n-type) Relationship between Eo and no in thermal equilibrium (from Je=0): One equation, one unknown. Given ND(x), can solve for no(x) (but in general, require numerical solution).

Doped semiconductor in thermal equilibrium If ND(x) changes slowly with x ⇒ no(x) will also change slowly, then: The majority carrier concentration closely tracks the doping level. When does this simple result apply? or Define Debye length:

Doped semiconductor in thermal equilibrium Rewrite condition: is change in electrostatic potential over a Debye length For a non-uniformly doped profile to be quasi-neutral in TE, the change in the electrostatic potential over a Debye length must be smaller than thermal voltage. LD is a characteristic length for electrostatic problems in semiconductors.

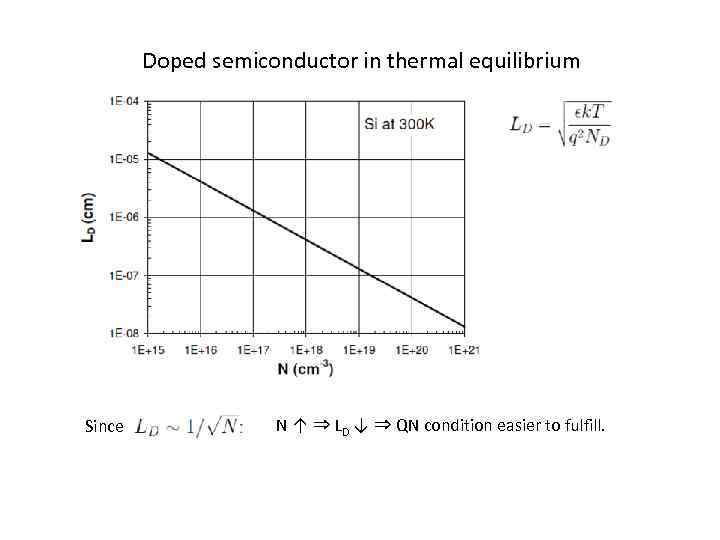Doped semiconductor in thermal equilibrium Since N ↑ ⇒ LD ↓ ⇒ QN condition easier to fulfill.

Basic Equations

Basic Equations Equation set difficult because of coupling through Gauss’ law. Two broad classes of important situations break Gauss’law coupling: 1. Carrier concentrations are high: quasi-neutral situation: 2. Carrier concentrations are very low: space-charge and high-resistivity situations:

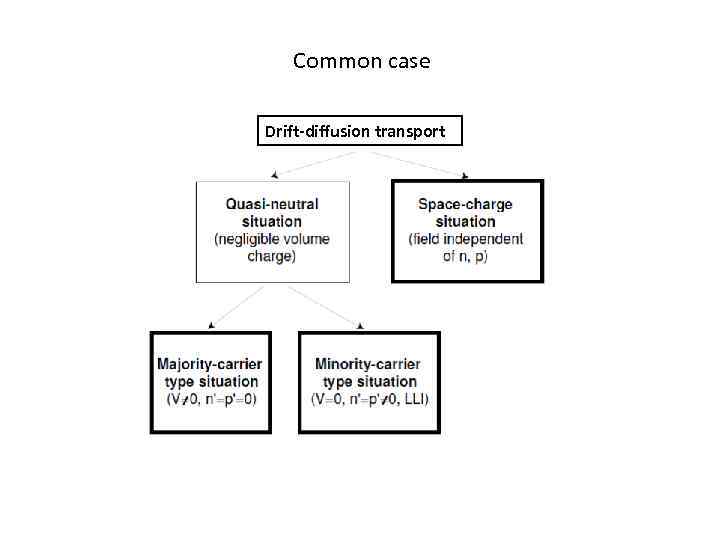Common case Drift-diffusion transport

Basic Equations: Quasi-neutral approximation At every location, the net volume charge that arises from a discrepancy of the concentration of positive and negative species is negligible in the scale of the charge density that is present. QN approximation eliminates Gauss’ law from the set: • Quasi-neutrality in equilibrium: • Additionally, quasi-neutrality outside equilibrium: • QN approximation good if n, p high ⇒ carriers move to erase ρ. • QN holds if length scale of problem >> Debye length LD

Basic Equations: Quasi-neutral approximation Consequence of quasi-neutrality Subtract one continuity equation from the other: continuity equation for net volume charge: if Jt changes with position, ρ changes with time. In Static case: In Dynamic case, in times scale of interest

Basic Equations: Quasi-neutral approximation Simplified set of basic equations for 1 D quasi-neutral situations

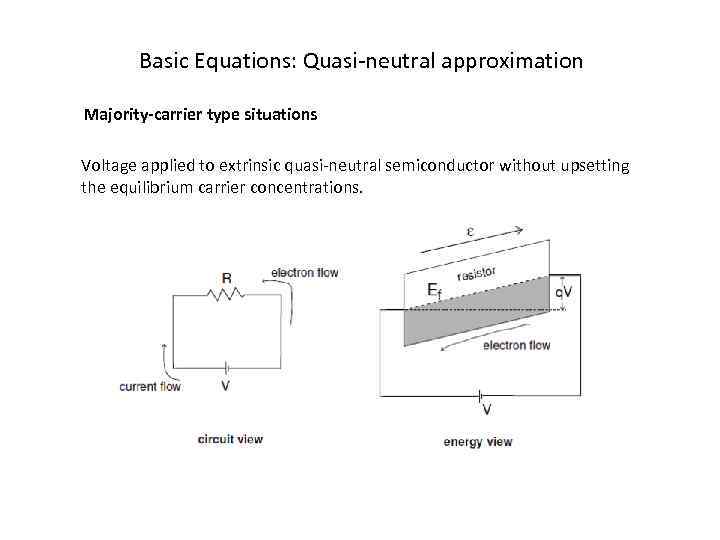Basic Equations: Quasi-neutral approximation Majority-carrier type situations Voltage applied to extrinsic quasi-neutral semiconductor without upsetting the equilibrium carrier concentrations.

Basic Equations: Quasi-neutral approximation Majority-carrier type situations Characteristics of majority carrier-type situations: • electric field imposed from outside • electrons and holes drift • electron and hole concentrations unperturbed from TE Simplifications: • neglect contribution of minority carriers • neglect time derivatives of carrier concentrations ⇒ problem becomes completely quasi-static

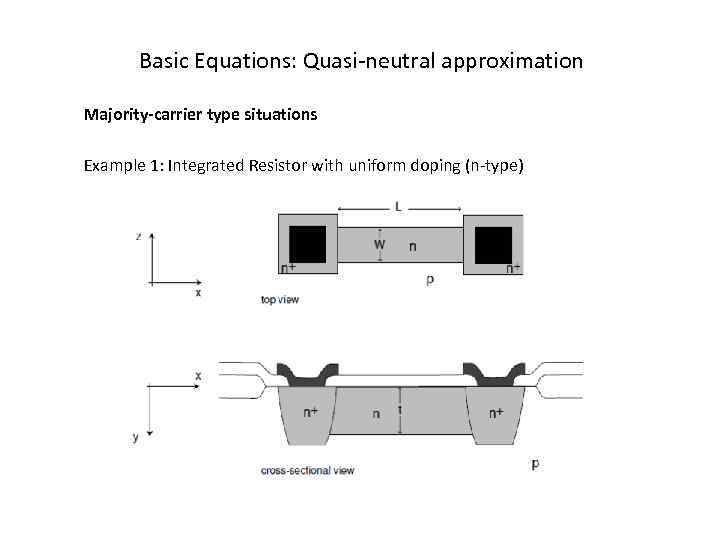Basic Equations: Quasi-neutral approximation Majority-carrier type situations Example 1: Integrated Resistor with uniform doping (n-type)

Basic Equations: Quasi-neutral approximation Majority-carrier type situations Example 1: Integrated Resistor with uniform doping (n-type) Uniform doping ⇒Eo = 0, then: If E not too high,

Basic Equations: Quasi-neutral approximation Minority-carrier type situations Situations characterized by: • excess carriers over TE • no external electric field applied (but small internal field generated by carrier injection: E= Eo + E’) Example: electron transport through base of npn BJT. Two approximations: 1. E small: 2. Low-level injection ⇒ for n-type: • negligible minority carrier drift due to E 0 (but can’t say the same about majority carriers)

Basic Equations: Quasi-neutral approximation Minority-carrier type situations • Majority-carrier current equation:

Basic Equations: Quasi-neutral approximation Minority-carrier type situations • Minority-carrier current equation: • Minority-carrier continuity equation:

Basic Equations: Quasi-neutral approximation Minority-carrier type situations Now plug in Jh from above: One differential equation with one unknown: p’.

Basic Equations: Quasi-neutral approximation Minority-carrier type situations

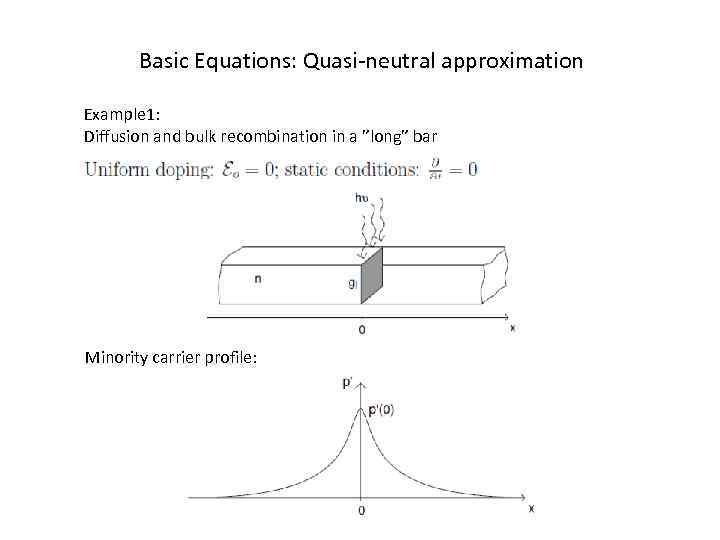Basic Equations: Quasi-neutral approximation Example 1: Diffusion and bulk recombination in a ”long” bar Minority carrier profile:

Basic Equations: Quasi-neutral approximation Majority carrier profile? N’= p’ exactly? Far away Jt =0 ⇒ Jt =0 everywhere.

Basic Equations: Quasi-neutral approximation

Basic Equations: Quasi-neutral approximation Step 1. Minority carrier flow problem(for x> 0): B. C. at x =0: Step 2. Hole current: Assuming

Basic Equations: Quasi-neutral approximation Step 3. Electron current:

Conclusions • Minority-carrier type situations dominated by behavior of minority carriers: diffusion, recombination and drift. • Minority-carrier type situations called that way because: -length and time scales of problem dominated by minority carrier behavior (diffusion, recombination, and drift). -role of majority carriers is to preserve quasi-neutrality and total current continuity