PHYSICS 231 Lecture 28 Thermal conduction Remco Zegers

PHYSICS 231 Lecture 28: Thermal conduction Remco Zegers Walk-in hour: Thursday 11: 30 -13: 30 am Helproom PHY 231 1

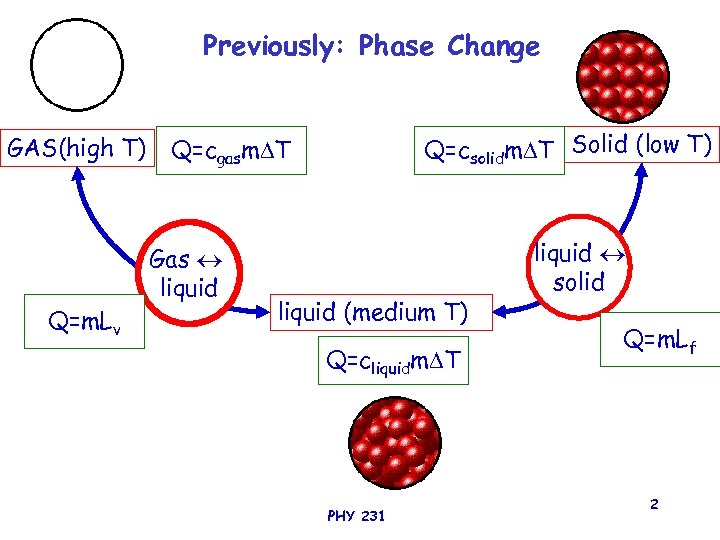Previously: Phase Change GAS(high T) Gas liquid Q=m. Lv Q=csolidm T Solid (low T) Q=cgasm T liquid (medium T) Q=cliquidm T PHY 231 liquid solid Q=m. Lf 2

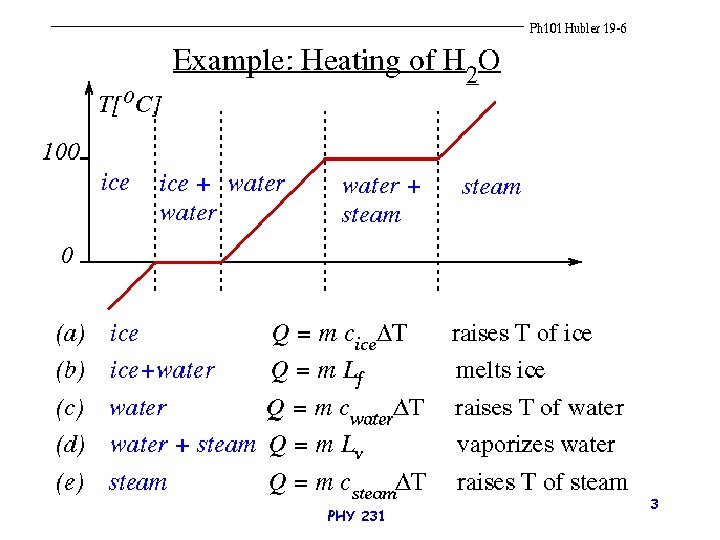PHY 231 3

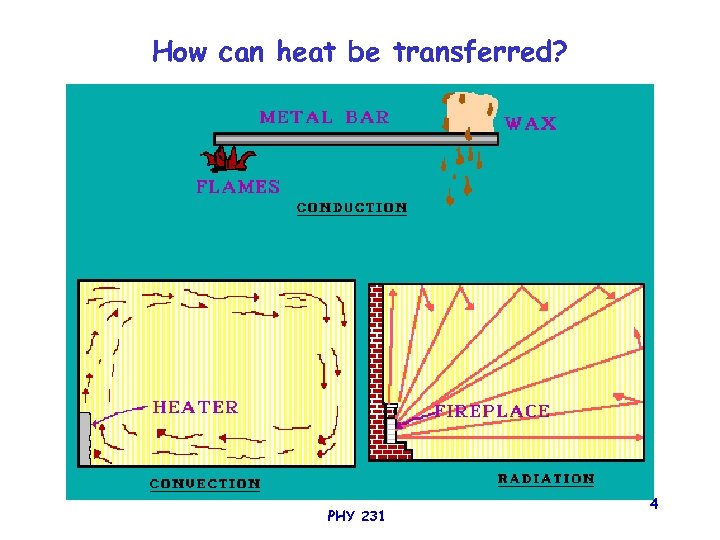How can heat be transferred? PHY 231 4

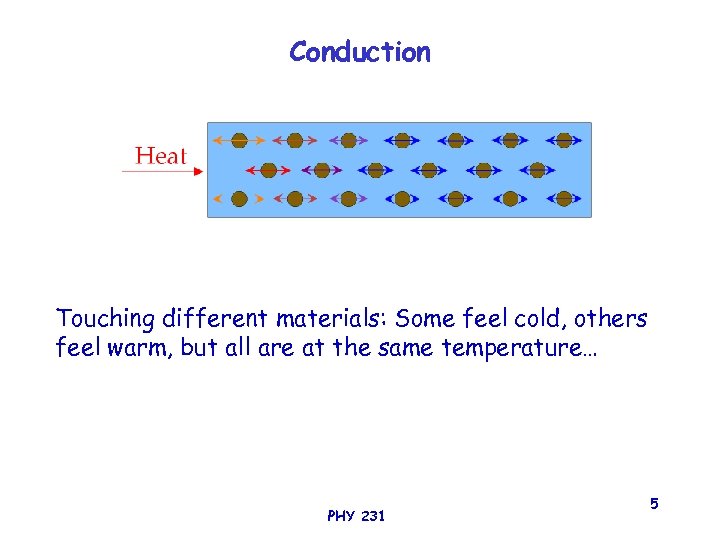Conduction Touching different materials: Some feel cold, others feel warm, but all are at the same temperature… PHY 231 5

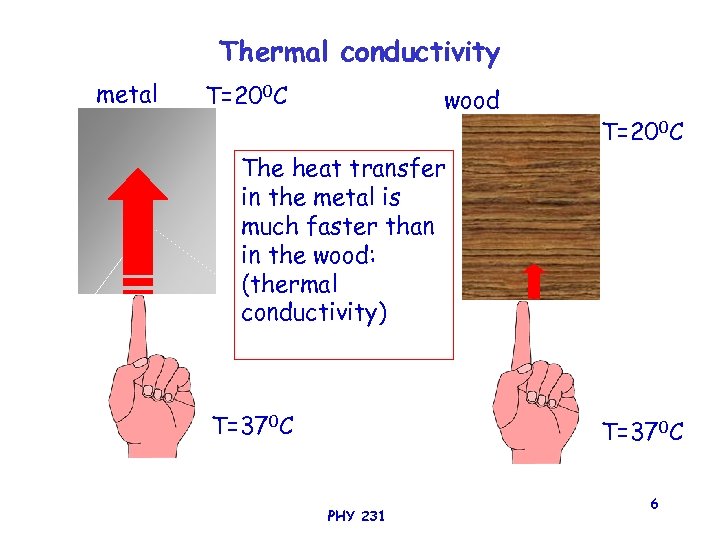Thermal conductivity metal T=200 C wood T=200 C The heat transfer in the metal is much faster than in the wood: (thermal conductivity) T=370 C PHY 231 6

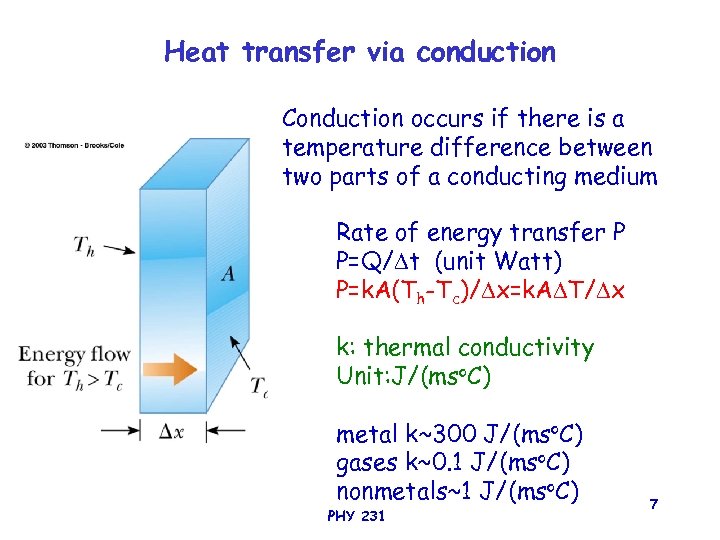Heat transfer via conduction Conduction occurs if there is a temperature difference between two parts of a conducting medium Rate of energy transfer P P=Q/ t (unit Watt) P=k. A(Th-Tc)/ x=k. A T/ x k: thermal conductivity Unit: J/(mso. C) metal k~300 J/(mso. C) gases k~0. 1 J/(mso. C) nonmetals~1 J/(mso. C) PHY 231 7

Example A glass window (A=4 m 2, x=0. 5 cm) separates a living room (T=200 C) from the outside (T=0 o. C). A) What is the rate of heat transfer through the window (kglass=0. 84 J/(mso. C))? B) By what fraction does it change if the surface becomes 2 x smaller and the temperature drops to -200 C? A) P=k. A T/ x=0. 84*4*20/0. 005=13440 Watt B) Porig=k. A T/ x Pnew=k(0. 5 A)(2 T)/ x=Porig The heat transfer is the same PHY 231 8

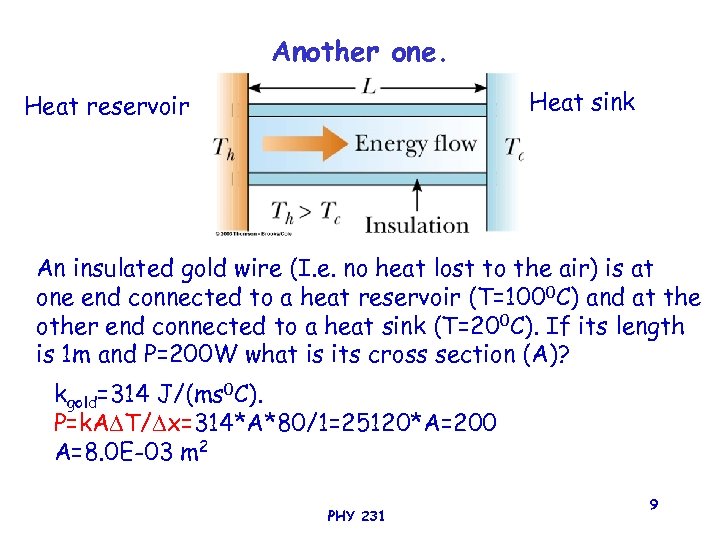Another one. Heat sink Heat reservoir An insulated gold wire (I. e. no heat lost to the air) is at one end connected to a heat reservoir (T=1000 C) and at the other end connected to a heat sink (T=200 C). If its length is 1 m and P=200 W what is its cross section (A)? kgold=314 J/(ms 0 C). P=k. A T/ x=314*A*80/1=25120*A=200 A=8. 0 E-03 m 2 PHY 231 9

Water 0. 5 L 1000 C And another A=0. 03 m 2 thickness: 0. 5 cm. 1500 C A student working for his exam feels hungry and starts boiling water (0. 5 L) for some noodles. He leaves the kitchen when the water just boils. The stove’s temperature is 1500 C. The pan’s bottom has dimensions given above. Working hard on the exam, he only comes back after half an hour. Is there still water in the pan? (Lv=540 cal/g, kpan=1 cal/(ms 0 C) To boil away 0. 5 L (=500 g) of water: Q=Lv*500=270000 cal Heat added by the stove: P=k. A T/ x=1*0. 03*50/0. 005= =300 cal P=Q/ t t=Q/P=270000/300=900 s (15 minutes) He’ll be hungry for a bit longer… PHY 231 10

inside Isolation Tc Th L 1 L 2 L 3 A house is built with 10 cm thick wooden walls and roofs. The owner decides to install insulation. After installation the walls and roof are 4 cm wood+2 cm isolation+4 cm wood. If kwood=0. 10 J/(ms 0 C) and kisolation=0. 02 J/(ms 0 C), by what factor does he reduce his heating bill? Pbefore=A T/[0. 10/0. 10]=A T Pafter=A T/[0. 04/0. 10+0. 02/0. 02+0. 04/0. 10]=0. 55 A T Almost a factor of 2 (1. 81)! PHY 231 11

Overview of material for exam: 8 =I (compare to F=ma) Moment of inertia I: I=( miri 2) (kgm 2) : angular acceleration (rad/s 2) I depends on the choice of rotation axis!! F F r r PHY 231 12

Chapter 8: Rotational KEr=½I 2 Conservation of energy for rotating object: [PE+KEt+KEr]initial= [PE+KEt+KEr]final [mgh+½mv 2+½I 2]initial= [mgh+½mv 2+½I 2]final PHY 231 13

Ch 8: Angular momentum =v/r L=I =mr 2 v/r =mvr Conservation of angular momentum If the net torque equal zero, the angular momentum L does not change Ii i=If f PHY 231 14

Chapter 9 Young’s modulus. PHY 231 15

Chapter 9 Shear modulus PHY 231 16

Chapter 9: Bulk modulus PHY 231 17

Chapter 9: density water=1. 0 x 103 kg/m 3 PHY 231 18

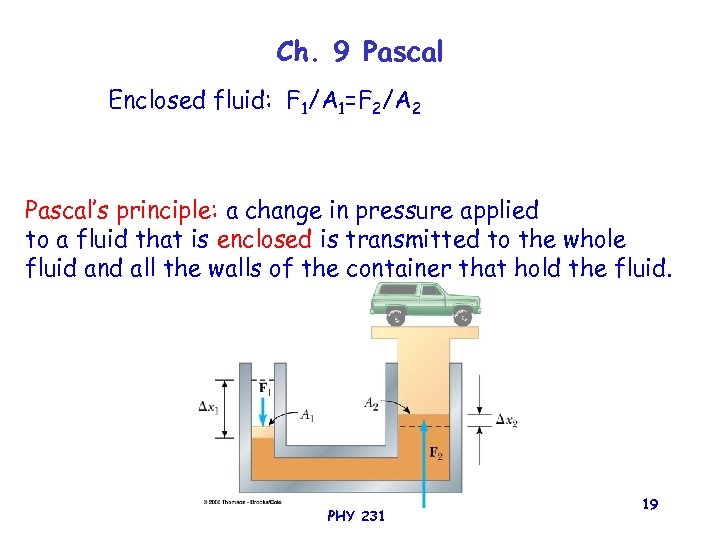Ch. 9 Pascal Enclosed fluid: F 1/A 1=F 2/A 2 Pascal’s principle: a change in pressure applied to a fluid that is enclosed is transmitted to the whole fluid and all the walls of the container that hold the fluid. PHY 231 19

Pressure at depth h P = P 0+ fluidgh h: distance between liquid surface and the point where you measure P P 0 h P Buoyant force for submerged object B = fluid. Vobjectg = Mfluidg = wfluid The buoyant force equals the weight of the amount of water that can be put in the volume taken by the object. If object is not moving: B=wobject= fluid Buoyant force for floating object The buoyant force equals the weight of the amount of water that can be put in the part of the volume of the object that is under water. object. Vobject= water. Vdisplaced h= object. Vobject/( water. A) PHY 231 B h w 20

Bernoulli’s equation P 1+½ v 12+ gy 1= P 2+½ v 22+ gy 2 P+½ v 2+ gy=constant The sum of the pressure (P), the kinetic energy per unit volume (½ v 2) and the potential energy per unit volume ( gy) is constant at all points along a path of flow. Note that for an incompressible fluid: A 1 v 1=A 2 v 2 This is called the equation of continuity. PHY 231 21

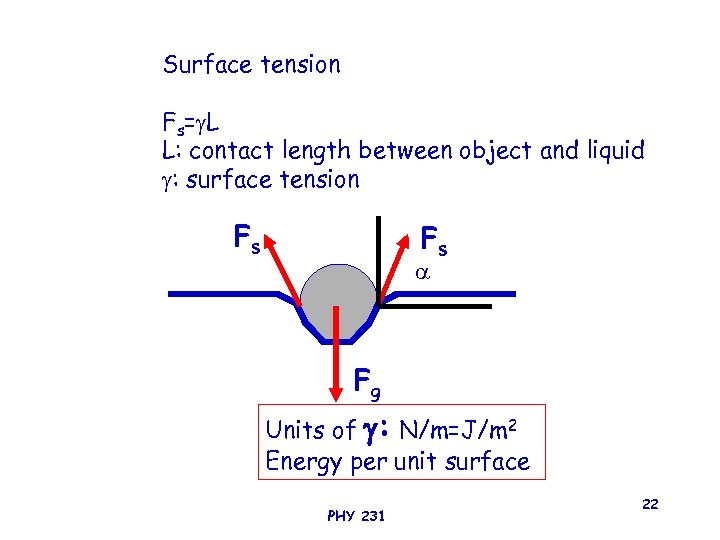Surface tension Fs= L L: contact length between object and liquid : surface tension Fs Fs Fg Units of : N/m=J/m 2 Energy per unit surface PHY 231 22

Poiseuille’s Law How fast does a fluid flow through a tube? Rate of flow Q= v/ t= R 4(P 1 -P 2) 8 L (unit: m 3/s) : coefficient of viscosity PHY 231 23

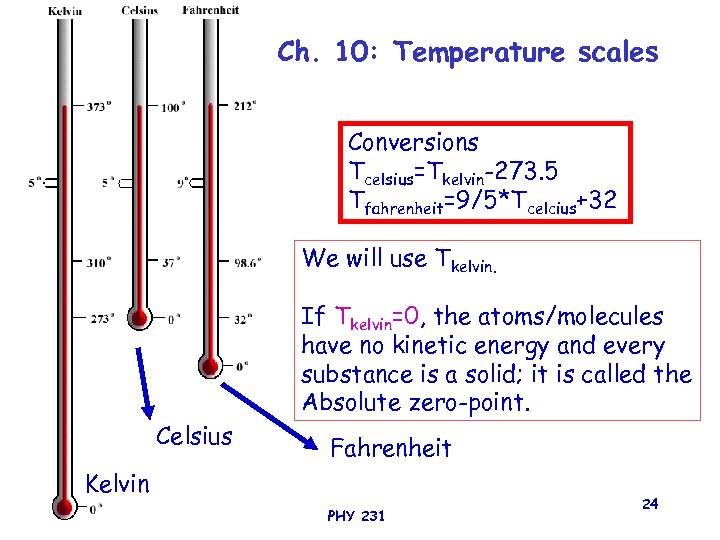Ch. 10: Temperature scales Conversions Tcelsius=Tkelvin-273. 5 Tfahrenheit=9/5*Tcelcius+32 We will use Tkelvin. If Tkelvin=0, the atoms/molecules have no kinetic energy and every substance is a solid; it is called the Absolute zero-point. Celsius Fahrenheit Kelvin PHY 231 24

Ch. 10: Thermal expansion length L L= Lo T surface A= Ao T =2 volume V= Vo T =3 L 0 : coefficient of linear expansion different for each material Some examples: =24 E-06 1/K Aluminum =1. 2 E-04 1/K Alcohol PHY 231 T=T 0+ T 25

Boyle & Charles & Gay-Lussac IDEAL GAS LAW PV/T = n. R = Nkb n: number of particles in the gas (mol) R: universal gas constant 8. 31 J/mol·K N: number of atoms/molecules kb: boltzmann’s constant 1. 38 x 10 -23 J/K n=N/NA NA: Avogadro’s constant 6. 02 x 1023 If no molecules are extracted from or added to a system: PHY 231 26

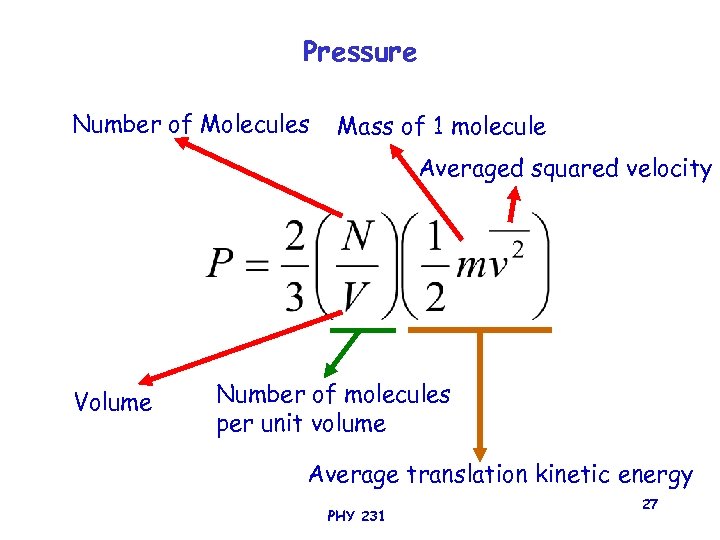Pressure Number of Molecules Mass of 1 molecule Averaged squared velocity Volume Number of molecules per unit volume Average translation kinetic energy PHY 231 27

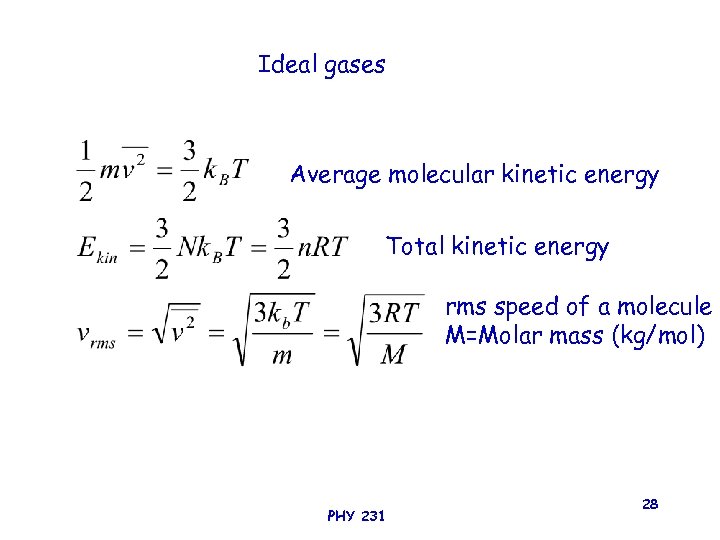Ideal gases Average molecular kinetic energy Total kinetic energy rms speed of a molecule M=Molar mass (kg/mol) PHY 231 28

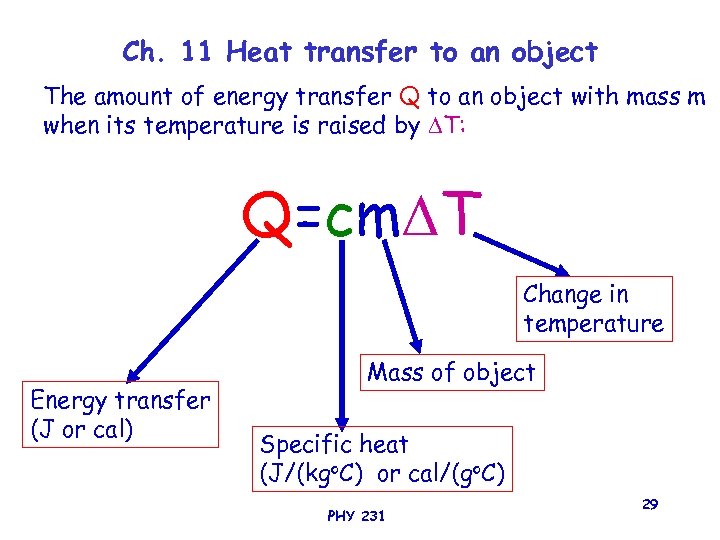Ch. 11 Heat transfer to an object The amount of energy transfer Q to an object with mass m when its temperature is raised by T: Q=cm T Change in temperature Energy transfer (J or cal) Mass of object Specific heat (J/(kgo. C) or cal/(go. C) PHY 231 29

Calorimetry If we connect two objects with different temperature energy will transferred from the hotter to the cooler one until their temperatures are the same. If the system is isolated: Qcold=-Qhot mcoldccold(Tfinal-Tcold)=-mhotchot(Tfinal-Thot) the final temperature is: Tfinal= PHY 231 mcoldccold. Tcold+mhotchot. Thot mcoldccold+mhotchot 30

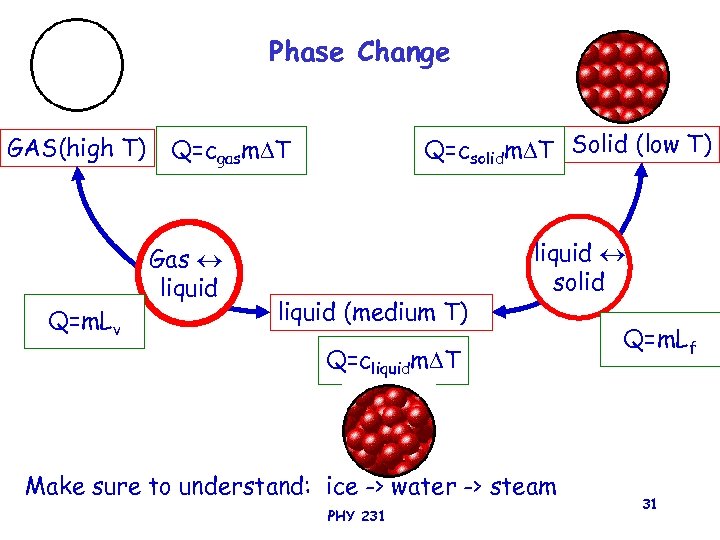Phase Change GAS(high T) Gas liquid Q=m. Lv Q=csolidm T Solid (low T) Q=cgasm T liquid (medium T) liquid solid Q=cliquidm T Make sure to understand: ice -> water -> steam PHY 231 Q=m. Lf 31

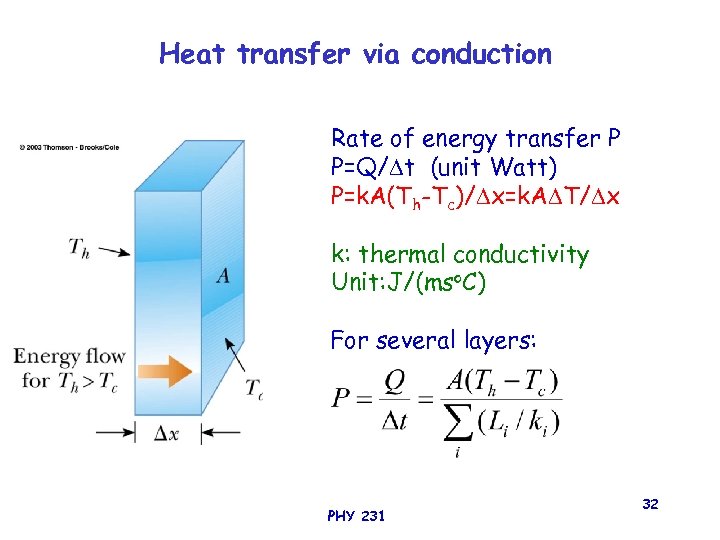Heat transfer via conduction Rate of energy transfer P P=Q/ t (unit Watt) P=k. A(Th-Tc)/ x=k. A T/ x k: thermal conductivity Unit: J/(mso. C) For several layers: PHY 231 32