Physics 2102 Jonathan Dowling Lecture 27 THU 29

Physics 2102 Jonathan Dowling Lecture 27: THU 29 APR 2010 Ch. 36: Diffraction

Radar: The Smaller The Wavelength the Better The Targeting Resolution X-band: =10 cm Ka-band: =1 cm K-band: =2 cm Laser: =1 m

Angles of the Secondary Maxima The diffraction minima are precisely at the angles where sin q = p l/a and a = pp (so that sin a=0). However, the diffraction maxima are not quite at the angles where sin q = (p+½) l/a and a = (p+½)p (so that |sin a|=1). 1 0. 00475 0. 0045 3 0. 00791 0. 0077 8 3 0. 01108 0. 01099 4 0. 01424 0. 01417 5 3 q. Max 2 l = 633 nm a = 0. 2 mm 2 (p+½) l/a 0. 01741 0. 01735 p 1 4 5 q (radians) To find the maxima, one must look near sin q = (p+½) l/a, for places where the slope of the diffraction pattern goes to zero, i. e. , where d[(sin a/a)2]/dq = 0. This is a transcendental equation that must be solved numerically. The table gives the q. Max solutions. Note that q. Max < (p+½) l/a.

Example: Diffraction of a laser through a slit 1. 2 cm Light from a helium-neon laser (l = 633 nm) passes through a narrow slit and is seen on a screen 2. 0 m behind the slit. The first minimum of the diffraction pattern is observed to be located 1. 2 cm from the central maximum. How wide is the slit?

Width of a Single-Slit Diffraction Pattern -y 1 0 w y 1 y 2 y 3

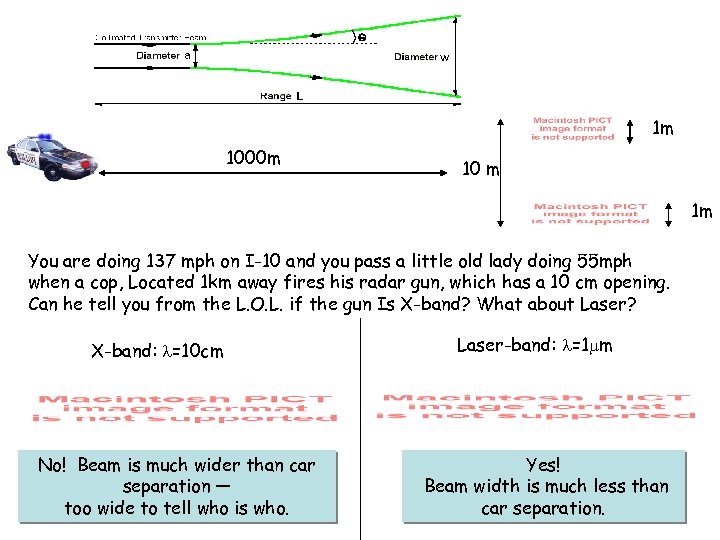1 m 1000 m 10 m 1 m You are doing 137 mph on I-10 and you pass a little old lady doing 55 mph when a cop, Located 1 km away fires his radar gun, which has a 10 cm opening. Can he tell you from the L. O. L. if the gun Is X-band? What about Laser? X-band: =10 cm No! Beam is much wider than car separation — too wide to tell who is who. Laser-band: =1 m Yes! Beam width is much less than car separation.

Exercise l 1 l 2 Two single slit diffraction patterns are shown. The distance from the slit to the screen is the same in both cases. Which of the following could be true? (a) The slit width a is the same for both; l 1>l 2. (b) The slit width a is the same for both; l 1p 2.

Combined Diffraction and Interference So far, we have treated diffraction and interference independently. However, in a two-slit system both phenomena should be present together. d a a Interference Only q (degrees) Diffraction Only q (degrees) Both q (degrees) Notice that when d/a is an integer, diffraction minima will fall on top of “missing” interference maxima.

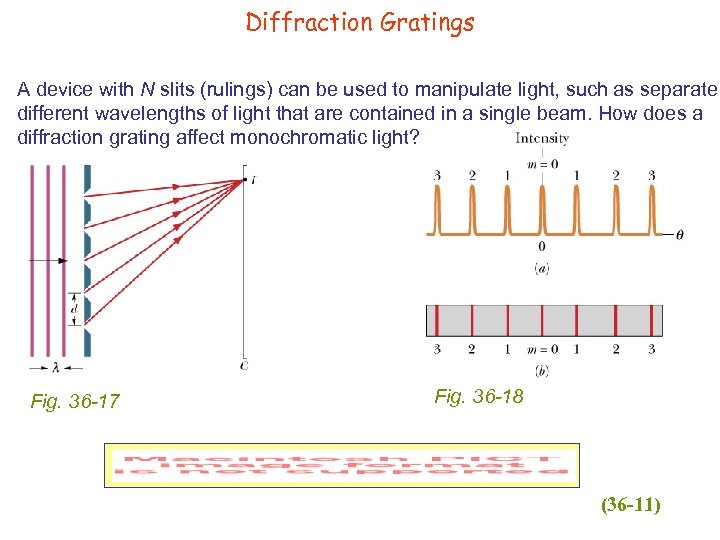Diffraction Gratings A device with N slits (rulings) can be used to manipulate light, such as separate different wavelengths of light that are contained in a single beam. How does a diffraction grating affect monochromatic light? Fig. 36 -17 Fig. 36 -18 (36 -11)

Circular Apertures Single slit of aperture a Hole of diameter D When light passes through a circular aperture instead of a vertical slit, the diffraction pattern is modified by the 2 D geometry. The minima occur at about 1. 22 l/D instead of l/a. Otherwise the behavior is the same, including the spread of the diffraction pattern with decreasing aperture.

The Rayleigh Criterion The Rayleigh Resolution Criterion says that the minimum separation to separate two objects is to have the diffraction peak of one at the diffraction minimum of the other, i. e. , Dq = 1. 22 l/D. Example: The Hubble Space Telescope has a mirror diameter of 4 m, leading to excellent resolution of close-lying objects. For light with wavelength of 500 nm, the angular resolution of the Hubble is Dq = 1. 53 x 10 -7 radians.

Example A spy satellite in a 200 km low-Earth orbit is imaging the Earth in the visible wavelength of 500 nm. How big a diameter telescope does it need to read a newspaper over your shoulder from Outer Space?

Example Solution Dq = 1. 22 l/D (The smaller the wavelength or the bigger the telescope opening — the better the angular resolution. ) Letters on a newspaper are about Dx = 10 mm apart. Orbit altitude R = 200 km & D is telescope diameter. R Formula: Dx = RDq = R(1. 22 /D) D = R(1. 22 /Dx) Dx = (200 x 103 m)(1. 22 x 500 x 10– 9 m)/(10 X 10– 3 m) = 12. 2 m Dq

Los Angeles from Space! Corona Declassified Spy Photo: Circa 1960’s

Some Professor’s House: Google Maps