Physics 207 Lecture 19 Nov 8 l Agenda

Physics 207, Lecture 19, Nov. 8 l Agenda: Chapter 14, Finish, Chapter 15, Start v Ch. 14: Fluid flow v Ch. 15: Oscillatory motion v Linear oscillator v Simple pendulum v Physical pendulum v Torsional pendulum Assignments: l Problem Set 7 due Nov. 14, Tuesday 11: 59 PM l For Monday, Finish Chapter 15, Start Chapter 16 Physics 207: Lecture 19, Pg 1

Fluids in Motion l Up to now we have described fluids in terms of their static properties: v Density r v Pressure p l To describe fluid motion, we need something that can describe flow: v Velocity v l There are different kinds of fluid flow of varying complexity v non-steady / steady v compressible / incompressible v rotational / irrotational v viscous / ideal Physics 207: Lecture 19, Pg 2

Types of Fluid Flow l Laminar flow v Each particle of the fluid follows a smooth path v The paths of the different particles never cross each other v The path taken by the particles is called a streamline l Turbulent flow v An irregular flow characterized by small whirlpool like regions v Turbulent flow occurs when the particles go above some critical speed Physics 207: Lecture 19, Pg 3

Types of Fluid Flow l Laminar flow v Each particle of the fluid follows a smooth path v The paths of the different particles never cross each other v The path taken by the particles is called a streamline l Turbulent flow v An irregular flow characterized by small whirlpool like regions v Turbulent flow occurs when the particles go above some critical speed Physics 207: Lecture 19, Pg 4

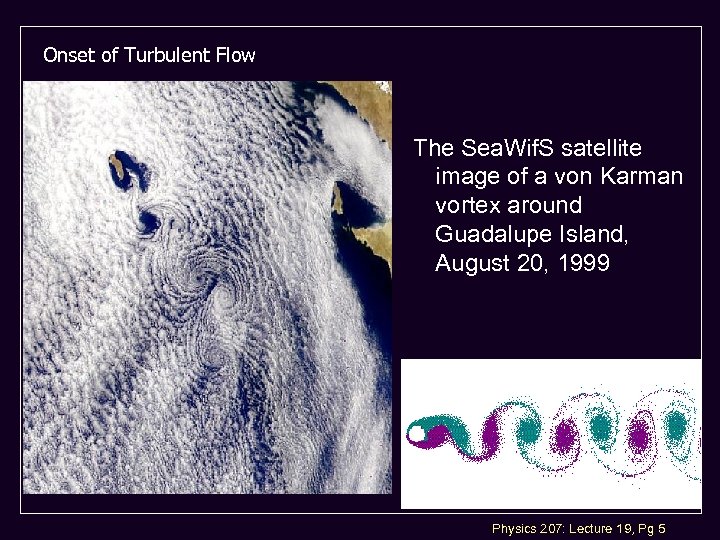Onset of Turbulent Flow The Sea. Wif. S satellite image of a von Karman vortex around Guadalupe Island, August 20, 1999 Physics 207: Lecture 19, Pg 5

Ideal Fluids l Fluid dynamics is very complicated in general (turbulence, vortices, etc. ) l Consider the simplest case first: the Ideal Fluid v No “viscosity” - no flow resistance (no internal friction) v Incompressible - density constant in space and time l Simplest situation: consider ideal fluid moving with steady flow velocity at each point in the flow is constant in time streamline l In this case, fluid moves on streamlines Physics 207: Lecture 19, Pg 6

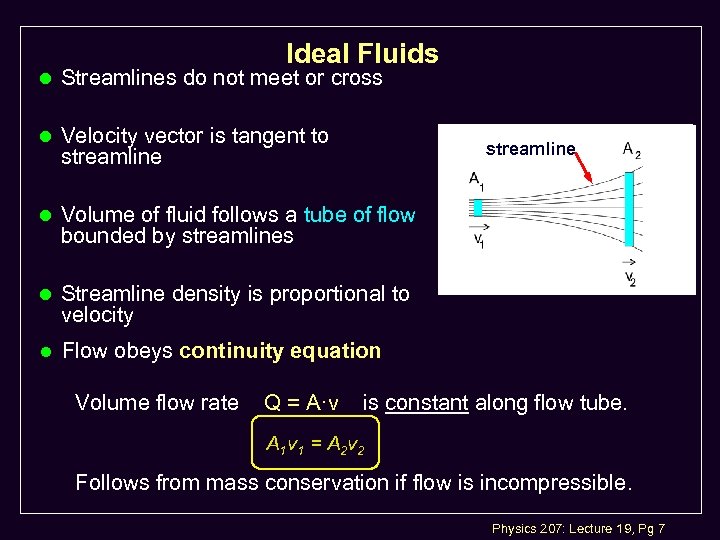Ideal Fluids l Streamlines do not meet or cross l Velocity vector is tangent to streamline l Volume of fluid follows a tube of flow bounded by streamlines l Streamline density is proportional to velocity l Flow obeys continuity equation Volume flow rate Q = A·v is constant along flow tube. A 1 v 1 = A 2 v 2 Follows from mass conservation if flow is incompressible. Physics 207: Lecture 19, Pg 7

Lecture 19 Exercise 1 Continuity l A housing contractor saves some money by reducing the size of a pipe from 1” diameter to 1/2” diameter at some point in your house. v 1/2 v Assuming the water moving in the pipe is an ideal fluid, relative to its speed in the 1” diameter pipe, how fast is the water going in the 1/2” pipe? (A) 2 v 1 (B) 4 v 1 (C) 1/2 v 1 (D) 1/4 v 1 Physics 207: Lecture 19, Pg 8

Conservation of Energy for Ideal Fluid l Recall the standard work-energy relation W = DK = Kf - Ki v Apply the principle to a section of flowing fluid with volume DV and mass Dm = r DV (here W is work done on fluid) v Net work by pressure difference over Dx (Dx 1 = v 1 Dt) v Focus first on W = F Dx W = F 1 Dx 1 – F 2 Dx 2 = (F 1/A 1) (A 1 Dx 1) – (F 2/A 2) (A 2 Dx 2) = P 1 DV 1 – P 2 DV 2 and DV 1 = DV 2 = DV (incompressible) DV W = (P 1– P 2 ) DV Bernoulli Equation P 1+ ½ r v 12 + r g y 1 = constant Physics 207: Lecture 19, Pg 9

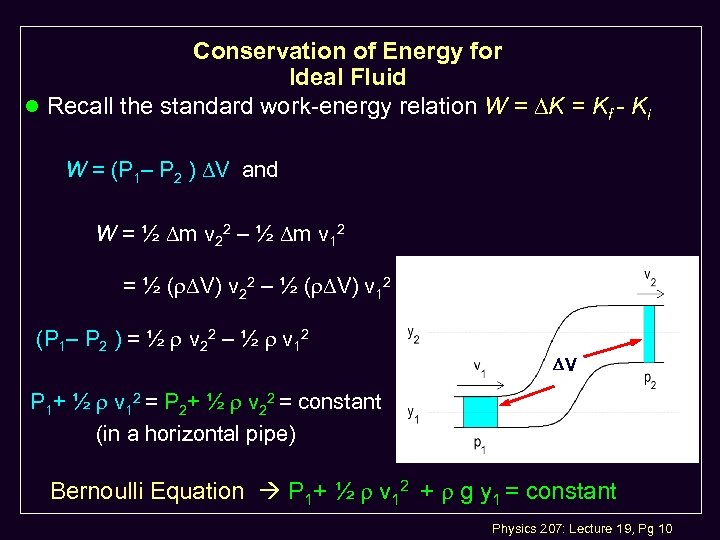Conservation of Energy for Ideal Fluid l Recall the standard work-energy relation W = DK = Kf - Ki W = (P 1– P 2 ) DV and W = ½ Dm v 22 – ½ Dm v 12 = ½ (r. DV) v 22 – ½ (r. DV) v 12 (P 1– P 2 ) = ½ r v 22 – ½ r v 12 DV P 1+ ½ r v 12 = P 2+ ½ r v 22 = constant (in a horizontal pipe) Bernoulli Equation P 1+ ½ r v 12 + r g y 1 = constant Physics 207: Lecture 19, Pg 10

Lecture 19 Exercise 2 Bernoulli’s Principle l A housing contractor saves some money by reducing the size of a pipe from 1” diameter to 1/2” diameter at some point in your house. v 1/2 2) What is the pressure in the 1/2” pipe relative to the 1” pipe? (A) smaller (B) same (C) larger Physics 207: Lecture 19, Pg 11

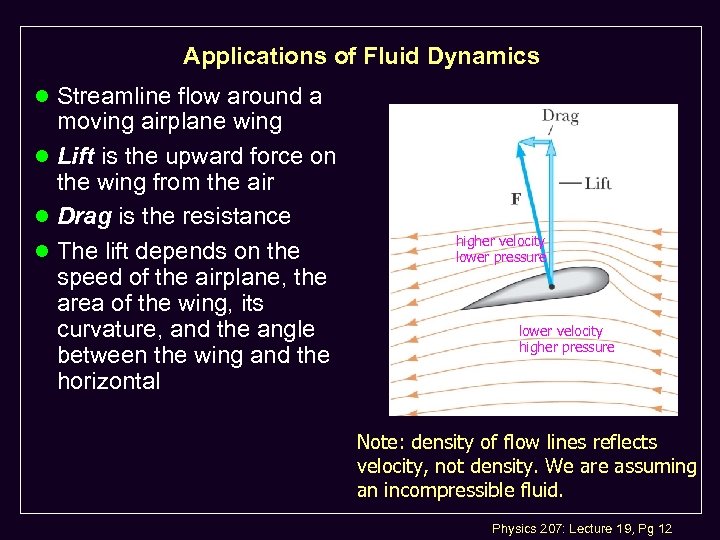Applications of Fluid Dynamics l Streamline flow around a moving airplane wing l Lift is the upward force on the wing from the air l Drag is the resistance l The lift depends on the speed of the airplane, the area of the wing, its curvature, and the angle between the wing and the horizontal higher velocity lower pressure lower velocity higher pressure Note: density of flow lines reflects velocity, not density. We are assuming an incompressible fluid. Physics 207: Lecture 19, Pg 12

Back of the envelope calculation l Boeing 747 -400 l Dimensions: v Length: 231 ft 10 inches v Wingspan: 211 ft 5 in v Height: 63 ft 8 in l Weight: v Empty: 399, 000 lb v Max Takeoff (MTO): 800, 000 lb v Payload: 249, 122 lb cargo l Performance: Let an area of 200 ft x 15 ft v Cruising Speed: 583 mph produce lift or 4. 5 x 105 in 2 v Range: 7, 230 nm or just 2. 2 x 105 lbs upshot l r (v 22 - v 12) / 2 = P 1 – P 2 = DP Let v 2 = 220. 0 m/s v 2 = 210 m/s 1. Downward deflection So DP = 3 x 103 Pa = 0. 03 atm 2. Bernoulli (a small part) or 0. 5 lbs/in 2 http: //www. geocities. com/galemcraig/ 3. Circulation theory Physics 207: Lecture 19, Pg 13

Venturi Bernoulli’s Eq. Physics 207: Lecture 19, Pg 14

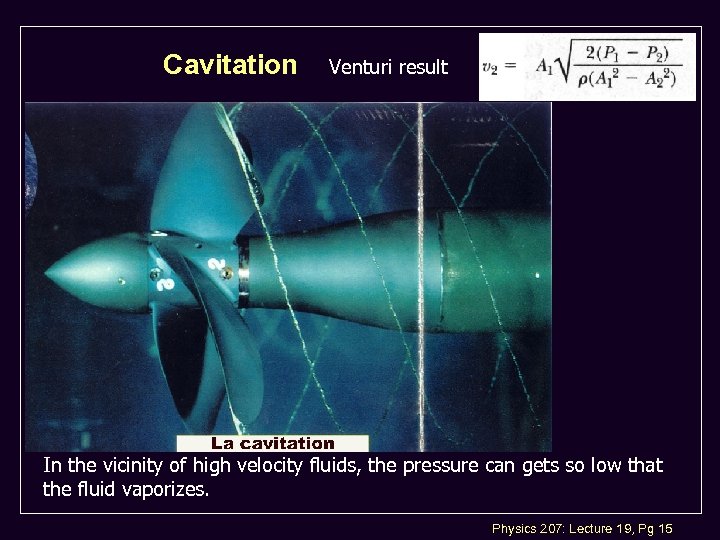Cavitation Venturi result In the vicinity of high velocity fluids, the pressure can gets so low that the fluid vaporizes. Physics 207: Lecture 19, Pg 15

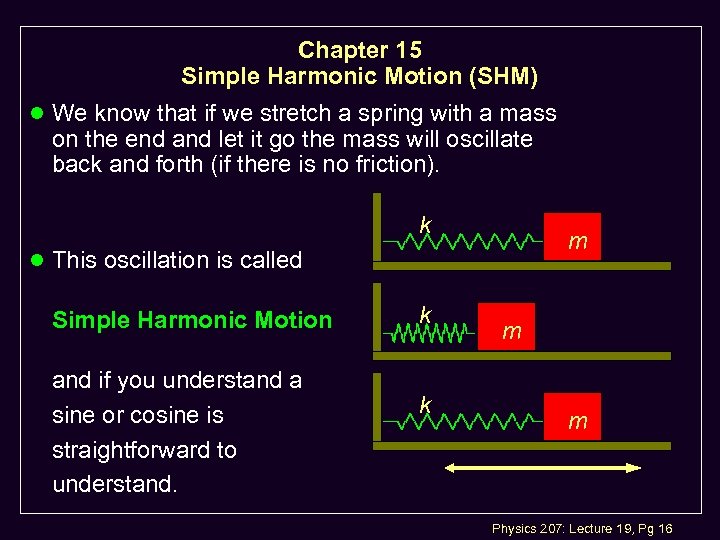Chapter 15 Simple Harmonic Motion (SHM) l We know that if we stretch a spring with a mass on the end and let it go the mass will oscillate back and forth (if there is no friction). k m l This oscillation is called Simple Harmonic Motion and if you understand a sine or cosine is straightforward to understand. k k m m Physics 207: Lecture 19, Pg 16

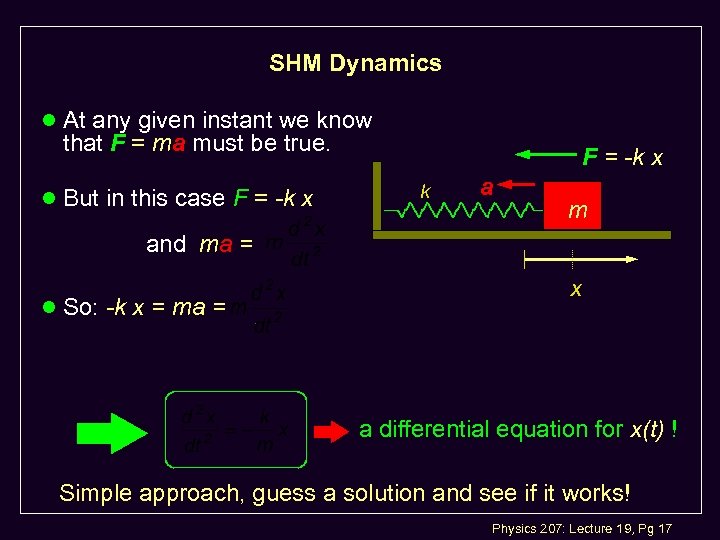SHM Dynamics l At any given instant we know that F = ma must be true. l But in this case F = -k x k a m and ma = l So: -k x = ma = x a differential equation for x(t) ! Simple approach, guess a solution and see if it works! Physics 207: Lecture 19, Pg 17

SHM Solution. . . l Either cos ( t ) or sin ( t ) can work l Below is a drawing of A cos ( t ) l where A = amplitude of oscillation T = 2 / A A Physics 207: Lecture 19, Pg 18

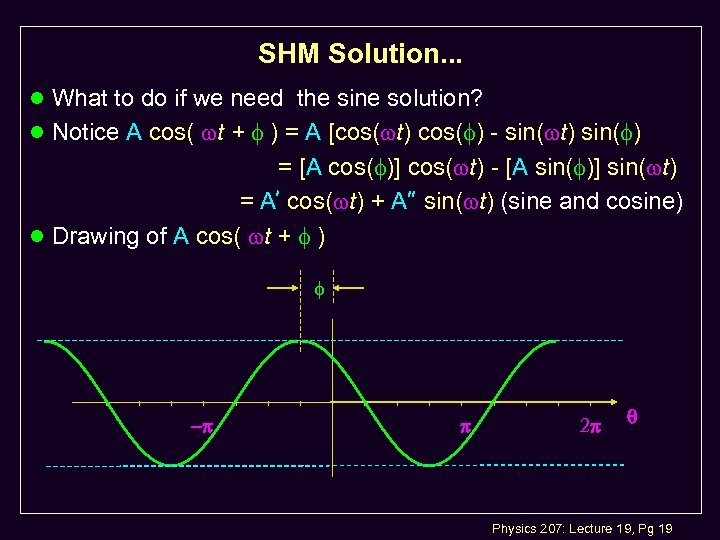SHM Solution. . . l What to do if we need the sine solution? l Notice A cos( t + ) = A [cos( t) cos( ) - sin( t) sin( ) = [A cos( )] cos( t) - [A sin( )] sin( t) = A’ cos( t) + A” sin( t) (sine and cosine) l Drawing of A cos( t + ) Physics 207: Lecture 19, Pg 19

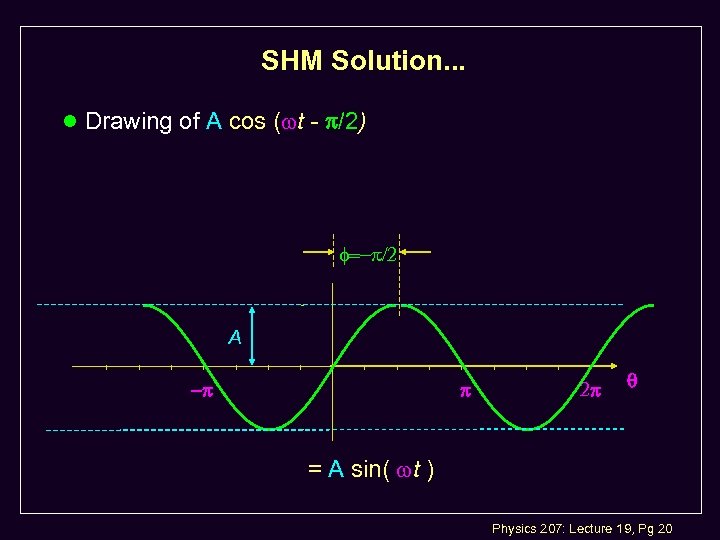SHM Solution. . . l Drawing of A cos ( t - /2) A = A sin( t ) Physics 207: Lecture 19, Pg 20

What about Vertical Springs? l For a vertical spring, if y is measured from the equilibrium position j l Recall: force of the spring is the negative derivative of this function: k l This will be just like the horizontal case: y=0 -ky = ma = m F= -ky Which has solution y(t) = A cos( t + ) where Physics 207: Lecture 19, Pg 21

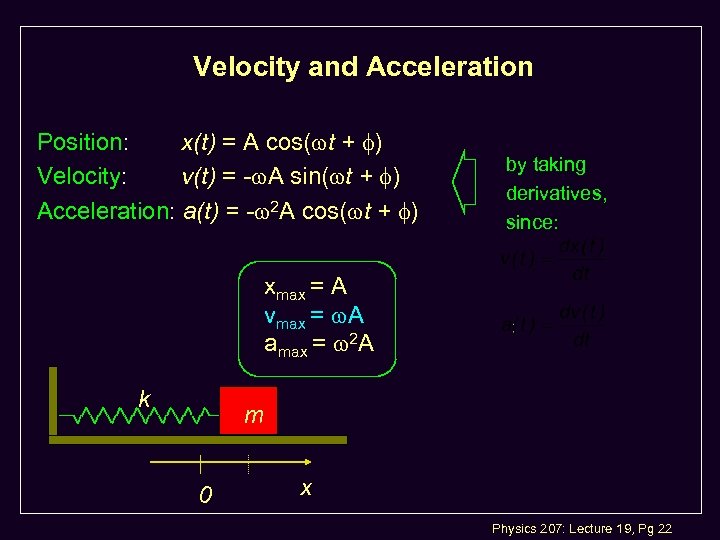Velocity and Acceleration Position: x(t) = A cos( t + ) Velocity: v(t) = - A sin( t + ) Acceleration: a(t) = - 2 A cos( t + ) by taking derivatives, since: xmax = A vmax = A amax = 2 A k m 0 x Physics 207: Lecture 19, Pg 22

Lecture 19, Exercise 3 Simple Harmonic Motion A mass oscillates up & down on a spring. It’s position as a function of time is shown below. At which of the points shown does the mass have positive velocity and negative acceleration ? Remember: velocity is slope and acceleration is the curvature l y(t) (a) (c) t (b) Physics 207: Lecture 19, Pg 23

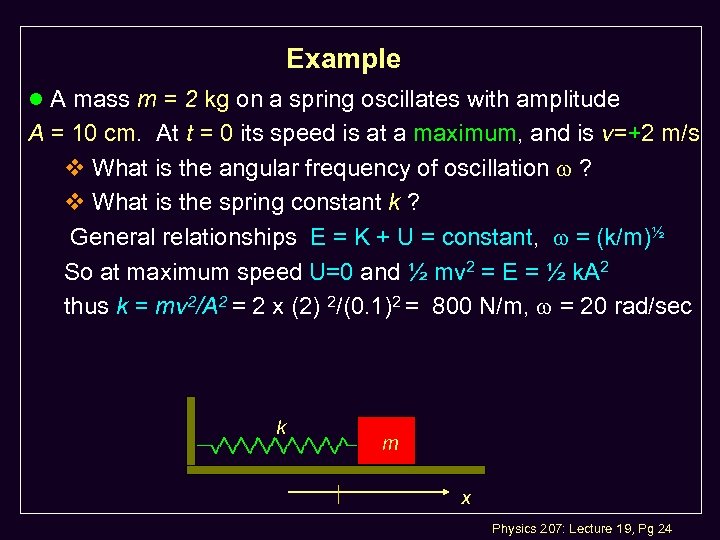Example l A mass m = 2 kg on a spring oscillates with amplitude A = 10 cm. At t = 0 its speed is at a maximum, and is v=+2 m/s v What is the angular frequency of oscillation ? v What is the spring constant k ? General relationships E = K + U = constant, = (k/m)½ So at maximum speed U=0 and ½ mv 2 = E = ½ k. A 2 thus k = mv 2/A 2 = 2 x (2) 2/(0. 1)2 = 800 N/m, = 20 rad/sec k m x Physics 207: Lecture 19, Pg 24

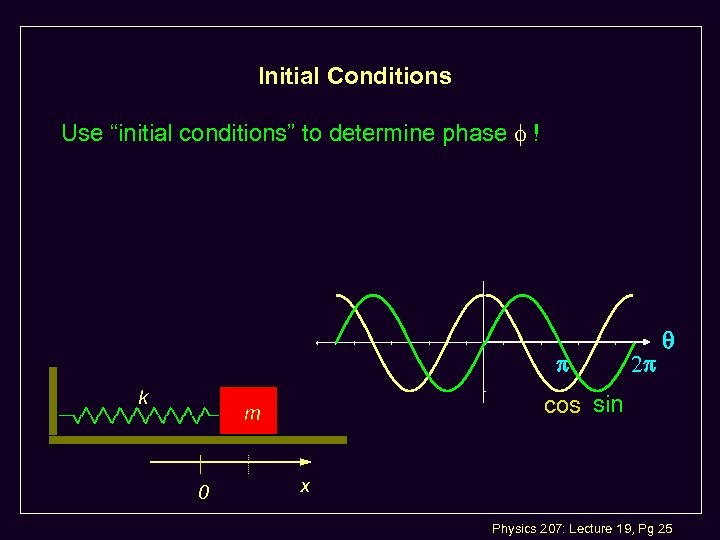Initial Conditions Use “initial conditions” to determine phase ! k cos sin m 0 x Physics 207: Lecture 19, Pg 25

Lecture 19, Example 4 Initial Conditions l A mass hanging from a vertical spring is lifted a distance d above equilibrium and released at t = 0. Which of the following describe its velocity and acceleration as a function of time (upwards is positive y direction): (A) v(t) = - vmax sin( t ) a(t) = -amax cos( t ) (B) v(t) = vmax sin( t ) a(t) = amax cos( t ) (C) v(t) = vmax cos( t ) a(t) = -amax cos( t ) t=0 k y m d 0 (both vmax and amax are positive numbers) Physics 207: Lecture 19, Pg 26

Energy of the Spring-Mass System We know enough to discuss the mechanical energy of the oscillating mass on a spring. Remember, x(t) = A cos( t + ) v(t) = - A sin( t + ) a(t) = - 2 A cos( t + ) Kinetic energy is always K = ½ mv 2 K = ½ m [ - A sin( t + )]2 And the potential energy of a spring is, U = ½ k x 2 U = ½ k [ A cos ( t + ) ]2 Physics 207: Lecture 19, Pg 27

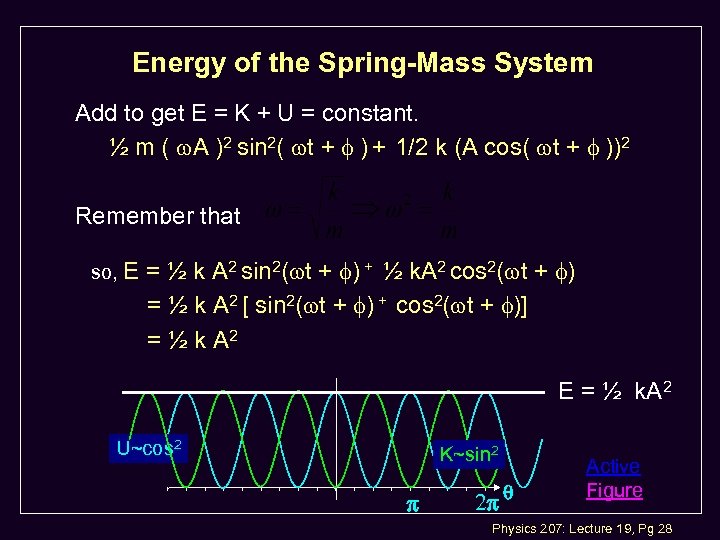Energy of the Spring-Mass System Add to get E = K + U = constant. ½ m ( A )2 sin 2( t + ) + 1/2 k (A cos( t + ))2 Remember that so, E = ½ k A 2 sin 2( t + ) + ½ k. A 2 cos 2( t + ) = ½ k A 2 [ sin 2( t + ) + cos 2( t + )] = ½ k A 2 E = ½ k. A 2 U~cos 2 K~sin 2 Active Figure Physics 207: Lecture 19, Pg 28

SHM So Far l The most general solution is x = A cos( t + ) where A = amplitude = (angular) frequency = phase constant l For SHM without friction, v The frequency does not depend on the amplitude ! v We will see that this is true of all simple harmonic motion! l The oscillation occurs around the equilibrium point where the force is zero! l Energy is a constant, it transfers between potential and kinetic. Physics 207: Lecture 19, Pg 29

The Simple Pendulum l A pendulum is made by suspending a mass m at the end of a string of length L. Find the frequency of oscillation for small displacements. z S Fy = mac = T – mg cos( ) = m v 2/L S Fx = max = -mg sin( ) If small then x L and sin( ) y dx/dt = L d /dt L 2 x/dt 2 = L d 2 /dt 2 ax = d x 2 / dt 2 L d 2 / dt 2 - g = 0 so ax = -g = L d T and = 0 cos( t + ) or = 0 sin( t + ) with = (g/L)½ m mg Physics 207: Lecture 19, Pg 30

The Rod Pendulum l A pendulum is made by suspending a thin rod of length L and mass M at one end. Find the frequency of oscillation for small displacements. S z = I = -| r x F | = (L/2) mg sin( ) z (no torque from T) -[ m. L 2/12 + m (L/2)2 ] L/2 mg T 2 /dt 2 = ½ g -1/3 L d The rest is for homework… x. CM L mg Physics 207: Lecture 19, Pg 31

General Physical Pendulum l Suppose we have some arbitrarily shaped solid of mass M hung on a fixed axis, that we know where the CM is located and what the moment of inertia I about the axis is. l The torque about the rotation (z) axis for small is (sin ) z-axis R = -Mg. R sin -Mg. R x. CM Mg where = 0 cos( t + ) Physics 207: Lecture 19, Pg 32

Torsion Pendulum l Consider an object suspended by a wire attached at its CM. The wire defines the rotation axis, and the moment of inertia I about this axis is known. l The wire acts like a “rotational spring”. v When the object is rotated, the wire is twisted. This produces a torque that opposes the rotation. v In analogy with a spring, the torque produced is proportional to the displacement: = - k where k is the torsional spring constant wire I v = (k/I)½ Physics 207: Lecture 19, Pg 33

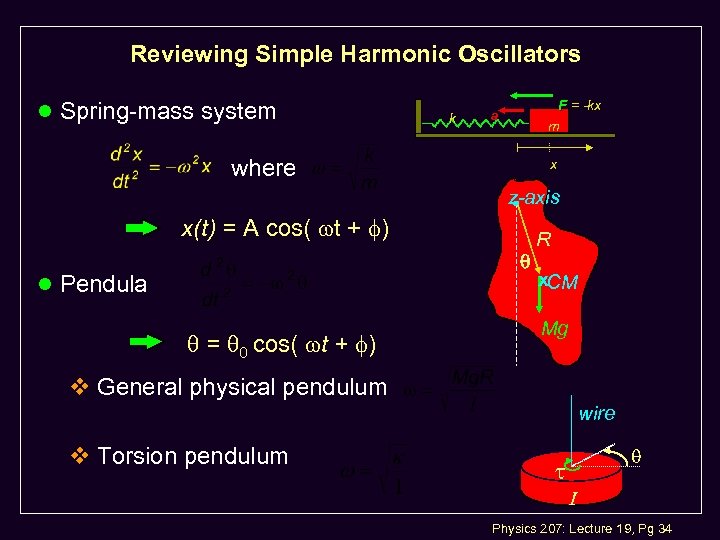Reviewing Simple Harmonic Oscillators l Spring-mass system k F = -kx m a where x z-axis x(t) = A cos( t + ) l Pendula = 0 cos( t + ) R x. CM Mg v General physical pendulum wire v Torsion pendulum I Physics 207: Lecture 19, Pg 34

Energy in SHM l For both the spring and the pendulum, we can derive the SHM solution using energy conservation. l The total energy (K + U) of a U system undergoing SMH will always be constant! E l This is not surprising since there are only conservative -A forces present, hence energy is conserved. K U 0 A x Physics 207: Lecture 19, Pg 35

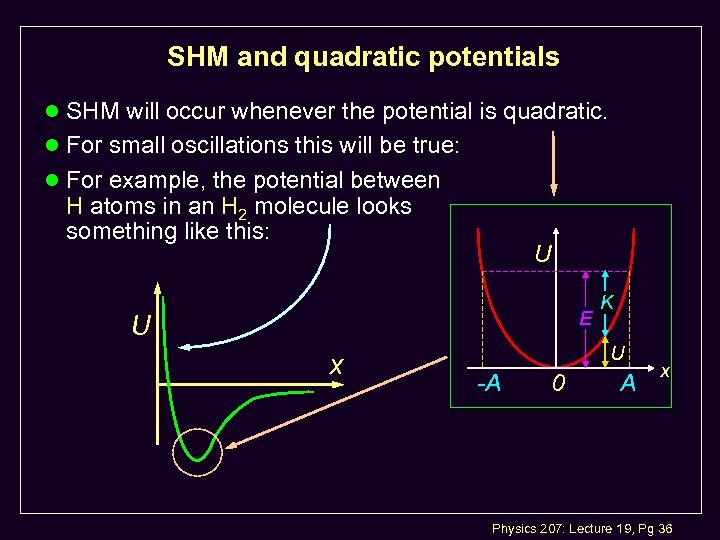SHM and quadratic potentials l SHM will occur whenever the potential is quadratic. l For small oscillations this will be true: l For example, the potential between H atoms in an H 2 molecule looks something like this: U E U x K U -A 0 A x Physics 207: Lecture 19, Pg 36

Lecture 19, Recap l Agenda: Chapter 14, Finish, Chapter 15, Start v Ch. 14: Fluid flow v Ch. 15: Oscillatory motion v Linear spring oscillator v Simple pendulum v Physical pendulum v Torsional pendulum Assignments: l Problem Set 7 due Nov. 14, Tuesday 11: 59 PM l For Monday, Finish Chapter 15, Start Chapter 16 Physics 207: Lecture 19, Pg 37