Physics 1501 Lecture 31 Today s Agenda l l

Physics 1501: Lecture 31 Today’s Agenda l l Homework #10 (due Friday Nov. 18) Midterm 2: Nov. 16 ç Students with schedule issues … Honor’s student … Topics: Fluids ç Pascal’s Principle (hydraulic lifts etc. ) ç Archimedes’ Principle ç Fluid dynamics ç Bernouilli’s equation ç Example of applications Physics 1501: Lecture 31, Pg 1

Fluids l What parameters do we use to describe fluids? ç Density units : kg/m 3 = 10 -3 g/cm 3 ç Pressure l units : 1 N/m 2 = 1 Pa (Pascal) Any force exerted by a fluid is perpendicular to a surface of contact, and is proportional to the area of that surface. ç Force (a vector) in a fluid can be expressed in terms of pressure (a scalar) as: n A Physics 1501: Lecture 31, Pg 2

Fluids l Bulk Modulus ç LIQUID: incompressible (density almost constant) ç GAS: compressible (density depends a lot on pressure) Gas (STP) Pb H 2 O Steel Bulk modulus (Pa=N/m 2) Physics 1501: Lecture 31, Pg 3

Pressure vs. Depth Incompressible Fluids (liquids) l When the pressure is much less than the bulk modulus of the fluid, we treat the density as constant independent of pressure: incompressible fluid l For an incompressible fluid, the density is the same everywhere, but the pressure is NOT! Physics 1501: Lecture 31, Pg 4

Pascal’s Principle l l So far we have discovered (using Newton’s Laws): ç Pressure depends on depth: p = rg y Pascal’s Principle addresses how a change in pressure is transmitted through a fluid. Any change in the pressure applied to an enclosed fluid is transmitted to every portion of the fluid and to the walls of the containing vessel. l Pascal’s Principle explains the working of hydraulic lifts ç i. e. the application of a small force at one place can result in the creation of a large force in another. ç Does this “hydraulic lever” violate conservation of energy? » Certainly hope not. . Let’s calculate. Physics 1501: Lecture 31, Pg 5

Pascal’s Principle l Consider the system shown: ç A downward force F 1 is applied to the piston of area A 1. ç This force is transmitted through the liquid to create an upward force F 2. ç Pascal’s Principle says that increased pressure from F 1 (F 1/A 1) is transmitted throughout the liquid. l F 2 > F 1 : Have we violated conservation of energy? ? Physics 1501: Lecture 31, Pg 6

Pascal’s Principle l Consider F 1 moving through a distance d 1. ç How large is the volume of the liquid displaced? ç This volume determines the displacement of the large piston. l Therefore the work done by F 1 equals the work done by F 2 We have NOT obtained “something for nothing”. Physics 1501: Lecture 31, Pg 7

Lecture 31, ACT 1 Hydraulics l Consider the systems shown to the right. ç In each case, a block of mass M is placed on the piston of the large cylinder, resulting in a difference d. I in the liquid levels. » If A 2 = 2´A 1, compare d. A and d. B. A) d. A = (1/2)d. B B) d. A = d. B d. A A 10 d. B C) d. A = 2 d. B M A 2 M A 10 » If A 10 = 2´A 20, compare d. A and d. C. A) d. A = (1/2)d. C B) d. A = d. C C) d. A = 2 d. C A 1 M A 20 Physics 1501: Lecture 31, Pg 8

Example Problems (1) l At what depth is the water pressure two atmospheres? It is one atmosphere at the surface. What is the pressure at the bottom of the deepest oceanic trench (about 104 meters)? Solution: P 2 = P 1 + rgd d is the depth. 2. 02 105 Pa = 1. 01 105 Pa The pressure increases + 103 kg/m 3*9. 8 m/s 2*d d = 10. 3 m one atmosphere for every 10 m. For d = 104 m: P 2 = 1. 01 105 Pa + 103 kg/m 3*9. 8 m/s 2*104 m = 9. 81 107 Pa = 971 Atm This assumes that water is incompressible. Physics 1501: Lecture 31, Pg 9

Example Problems (2) l Two masses rest on two pistons in a U-shaped tube of water, as shown. If M 1 = 3 kg and M 2 = 4. 5 kg, what is the height difference, h? The area of piston 1 is A 1 = 200 cm 2, and the area of piston 2 is A 2 = 100 cm 2. M 1 h M 2 Solution: M 1 g/A 1 + rgh = M 2 g/A 2 h = (M 2/A 2 -M 1/A 1)/r = 0. 3 m The pressure difference due to the two masses must be balanced by the water pressure due to h. Note that g does not appear in the answer. Physics 1501: Lecture 31, Pg 10

Using Fluids to Measure Pressure l Use Barometer to measure Absolute Pressure ç Top of tube evacuated (p=0) ç Bottom of tube submerged into pool of mercury open to atmosphere (p=p 0) ç Pressure dependence on depth: Barometer Physics 1501: Lecture 31, Pg 11

Using Fluids to Measure Pressure l Use Manometer to measure Gauge Pressure ç Measure pressure of volume (p 1) relative to atmospheric pressure (º gauge pressure) ç The height difference ( h) measures the gauge pressure Manometer p 1 p 0 h 1 atm = 760 mm (29. 9 in) Hg = 10. 3 m (33. 8 ft) H 20 Physics 1501: Lecture 31, Pg 12

Archimedes’ Principle l Suppose we weigh an object in air (1) and in water (2). ç How do these weights compare? W 1 < W 2 W 1 = W 2 W 1 > W 2 ç Why? » Since the pressure at the bottom of the object is greater than that at the top of the object, the water exerts a net upward force, the buoyant force, on the object. W 1 W 2 ? Physics 1501: Lecture 31, Pg 13

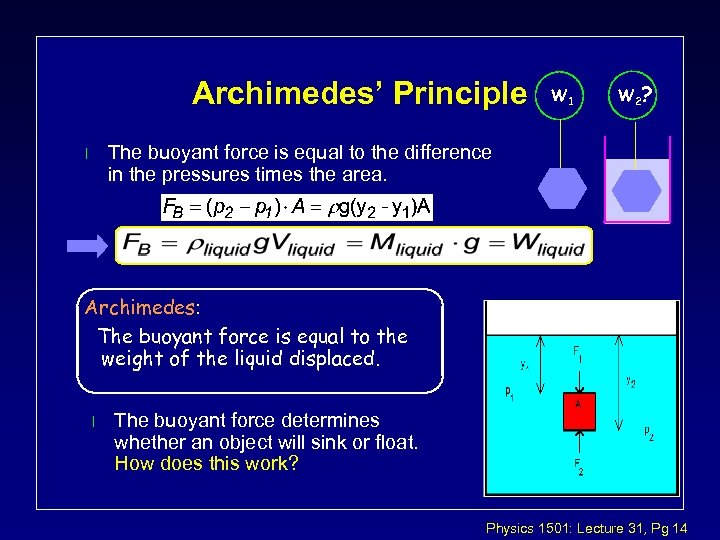Archimedes’ Principle W 1 W 2 ? The buoyant force is equal to the difference in the pressures times the area. l Archimedes: The buoyant force is equal to the weight of the liquid displaced. l The buoyant force determines whether an object will sink or float. How does this work? Physics 1501: Lecture 31, Pg 14

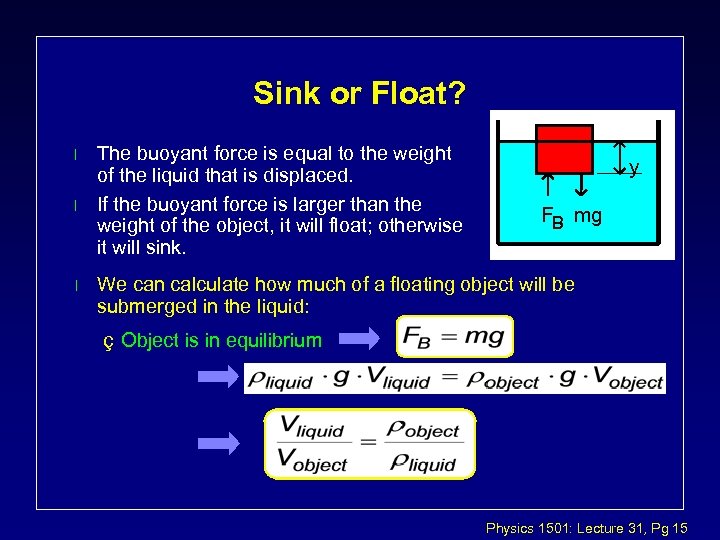Sink or Float? l l l The buoyant force is equal to the weight of the liquid that is displaced. If the buoyant force is larger than the weight of the object, it will float; otherwise it will sink. y FB mg We can calculate how much of a floating object will be submerged in the liquid: ç Object is in equilibrium Physics 1501: Lecture 31, Pg 15

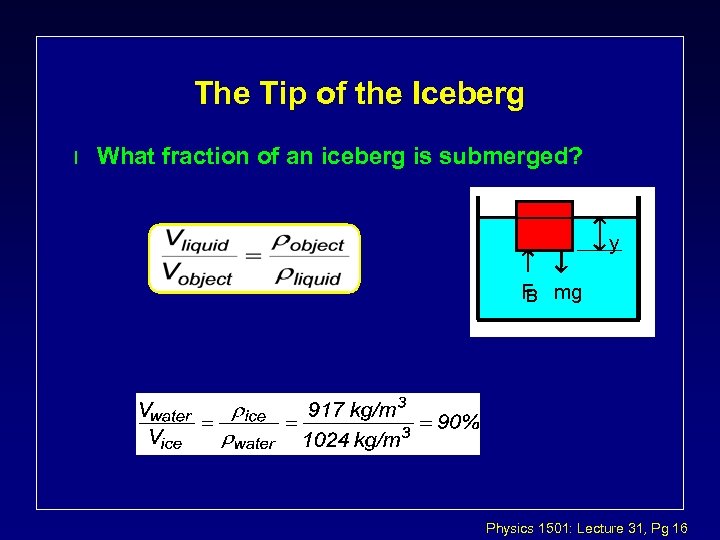The Tip of the Iceberg l What fraction of an iceberg is submerged? y F mg B Physics 1501: Lecture 31, Pg 16

Lecture 31, ACT 2 Buoyancy l A) A lead weight is fastened to a large styrofoam block and the combination floats on water with the water level with the top of the styrofoam block as shown. ç If you turn the styrofoam+Pb upside down, what happens? It sinks B) C) Pb styrofoam D) styrofoam Pb Physics 1501: Lecture 31, Pg 17

ACT 2 -A More Fun With Buoyancy l Cup I Two cups are filled to the same level with water. One of the two cups has plastic balls floating in it. ç Which cup weighs more? (A) Cup I (B) Cup II (C) the same Cup II (D) can’t tell Physics 1501: Lecture 31, Pg 18

ACT 2 -B Even More Fun With Buoyancy l A plastic ball floats in a cup of water with half of its volume submerged. Next some oil (roil < rball < rwater) is slowly added to the container until it just covers the ball. ç Relative to the water level, the ball will: (A) move up (B) move down l oi water (C) stay in same place Physics 1501: Lecture 31, Pg 19

Fluids in Motion l Up to now we have described fluids in terms of their static properties: ç density r ç pressure p l To describe fluid motion, we need something that can describe flow: ç velocity v l There are different kinds of fluid flow of varying complexity ç non-steady / steady ç compressible / incompressible ç rotational / irrotational ç viscous / ideal Physics 1501: Lecture 31, Pg 20

Ideal Fluids l l Fluid dynamics is very complicated in general (turbulence, vortices, etc. ) Consider the simplest case first: the Ideal Fluid ç no “viscosity” - no flow resistance (no internal friction) ç incompressible - density constant in space and time l Simplest situation: consider ideal fluid moving with steady flow - velocity at each point in the flow is constant in time l In this case, fluid moves on streamlines streamline Physics 1501: Lecture 31, Pg 21

Ideal Fluids l streamlines do not meet or cross l velocity vector is tangent to streamline l volume of fluid follows a tube of flow bounded by streamlines l Flow obeys continuity equation ç volume flow rate Q = A·v streamline is constant along flow tube. A 1 v 1 = A 2 v 2 ç follows from mass conservation if flow is incompressible. Physics 1501: Lecture 31, Pg 22

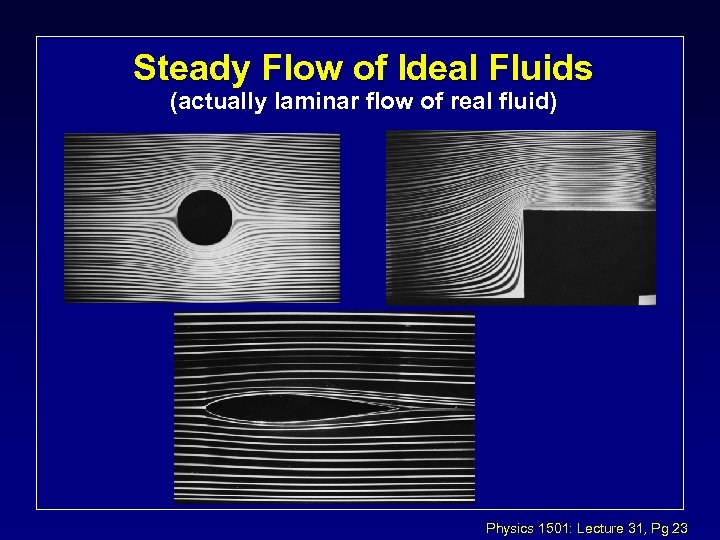Steady Flow of Ideal Fluids (actually laminar flow of real fluid) Physics 1501: Lecture 31, Pg 23

Lecture 31 Act 3 Continuity l A housing contractor saves some money by reducing the size of a pipe from 1” diameter to 1/2” diameter at some point in your house. v 1/2 1) Assuming the water moving in the pipe is an ideal fluid, relative to its speed in the 1” diameter pipe, how fast is the water going in the 1/2” pipe? a) 2 v 1 b) 4 v 1 c) 1/2 v 1 c) 1/4 v 1 Physics 1501: Lecture 31, Pg 24

Conservation of Energy for Ideal Fluid l Recall the standard work-energy relation ç Apply the principle to a section of flowing fluid with volume d. V and mass dm = r d. V (here W is work done on fluid) d. V Bernoulli Equation Physics 1501: Lecture 31, Pg 25

Lecture 31 Act 4 Bernoulli’s Principle l A housing contractor saves some money by reducing the size of a pipe from 1” diameter to 1/2” diameter at some point in your house. v 1/2 2) What is the pressure in the 1/2” pipe relative to the 1” pipe? a) smaller b) same c) larger Physics 1501: Lecture 31, Pg 26

Some applications l Lift for airplane wing l Enhance sport performance l More complex phenomena: ex. turbulence Physics 1501: Lecture 31, Pg 27

More applications l Vortices: ex. Hurricanes l And much more … Physics 1501: Lecture 31, Pg 28

Ideal Fluid: Bernoulli Applications l Bernoulli says: high velocities go with low pressure l Airplane wing ç shape leads to lower pressure on top of wing ç faster flow lower pressure lift » air moves downward at downstream edge wing moves up Physics 1501: Lecture 31, Pg 29

Ideal Fluid: Bernoulli Applications l Warning: the explanations in text books are generally oversimplified! l Curve ball (baseball), slice or topspin (golf) ç ball drags air around (viscosity) ç air speed near ball higher on bottom ç lower pressure force sideways acceleration or lift Physics 1501: Lecture 31, Pg 30

Ideal Fluid: Bernoulli Applications l Bernoulli says: high velocities go with low pressure l “Atomizer” ç moving air ‘sweeps’ air away from top of tube ç pressure is lowered inside the tube ç air pressure inside the jar drives liquid up into tube Physics 1501: Lecture 31, Pg 31

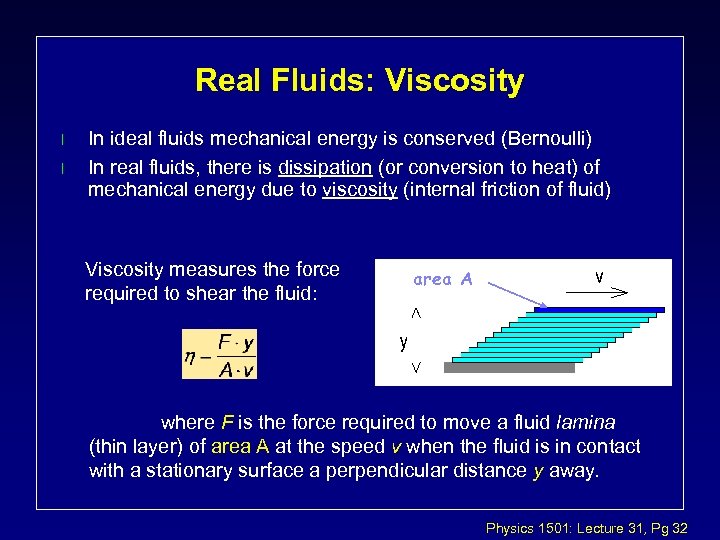Real Fluids: Viscosity l l In ideal fluids mechanical energy is conserved (Bernoulli) In real fluids, there is dissipation (or conversion to heat) of mechanical energy due to viscosity (internal friction of fluid) Viscosity measures the force required to shear the fluid: area A where F is the force required to move a fluid lamina (thin layer) of area A at the speed v when the fluid is in contact with a stationary surface a perpendicular distance y away. Physics 1501: Lecture 31, Pg 32

Real Fluids: Viscosity l Viscosity arises from particle collisions in the fluid ç as particles in the top layer diffuse downward they transfer some of their momentum to lower layers area A ç lower layers get pulled along (F = p/ t) air H 2 O oil glycerin Viscosity (Pa-s) Physics 1501: Lecture 31, Pg 33

Real Fluids: Viscous Flow l How fast can viscous fluid flow through a pipe? ç Poiseuille’s Law L p+ p Q r p R l Because friction is involved, we know that mechanical energy is not being conserved - work is being done by the fluid. l Power is dissipated when viscous fluid flows: P = v·F = Q · p the velocity of the fluid remains constant power goes into heating the fluid: increasing its entropy Physics 1501: Lecture 31, Pg 34

l Lecture 31 Act 5 Viscous flow Consider again the 1 inch diameter pipe and the 1/2 inch diameter pipe. L/2 1) Given that water is viscous, what is the ratio of the flow rates, Q 1/2, in pipes of these sizes if the pressure drop per meter of pipe is the same in the two cases? a) 3/2 b) 2 c) 4 Physics 1501: Lecture 31, Pg 35